基于改进灰色马尔可夫链的电传动装甲车辆负载需求功率预测
刘春光, 陈路明, 张运银, 张征,2, 徐浩轩
(1.陆军装甲兵学院 兵器与控制系, 北京 100072; 2.北京市遥感信息研究所, 北京 100192)
0 引言
电传动装甲车辆具有静音行驶、灵活转向、动力性强等特点,成为未来装甲车辆的重要发展方向[1]。但由于装甲车辆工作环境复杂,路况特征难以预先建模,且车辆大多工作于非道路工况,使得其功率变化呈现较强的随机变化特征,给负载功率预测带来较大困难,制约了现有车辆能量管理策略控制效果的进一步提升,迫切需要开发高水平的负载功率预测方法。
根据初始预测物理量的不同,现有车辆负载需求功率预测方法主要可以分为直接预测和间接预测两大类。其中,直接预测方法以当前时刻负载需求功率为参考量,采用单一或组合预测方法对负载需求功率进行直接预测。文献[2]采用径向基函数神经网络方法,对燃料电池汽车整车驱动功率进行预测,为优化控制策略提供了重要参考信息,降低了整车能耗。文献[3]依据记录的历史功率信息,采用统计分析方法,对电动车辆负载功率进行周期性预测,提升了智能充电系统的运行效率。
上述直接功率预测方法主要应用在公共汽车、固定轨道交通工具等行驶路线固定、周期性较强的场景,与电传动装甲车辆工作环境差异较大,难以直接移植到装甲车辆负载功率预测场景。间接预测方法并不直接对功率进行预测,而是通过对车速等其他直接可测的物理量进行预测后,再间接计算得到车辆的负载需求功率。文献[4]以混合动力越野车辆负载需求功率为研究对象,采用自适应马尔可夫链预测方法对寻优域中的车速变化情况进行预测,再依据车辆运动学公式间接计算得到车辆负载需求功率信息,有效提升了整车动力性和燃油经济性,但这种间接功率预测方法依赖于精确的环境参数,如地面摩擦系数、风速、坡度等,在时变参数较多且获取较为困难时,功率计算精度难以得到保证。文献[5]针对电传动车辆分布式驱动结构特点,采用轮毂驱动电机转速和转矩作为预测输入信号,计算得到短时整车负载需求功率,作为能量管理策略的参考输入信息,提升了车载供电系统的稳定性。该方法虽然可以得到较为精确的预测功率,但由于电机状态变化较为迅速,因此预测时域极短,难以实现多步功率预测[6]。
本文针对电传动装甲车辆负载变化呈现强随机性的特点,提出一种基于改进灰色马尔可夫链的组合功率预测方法,以实现对车辆负载需求功率的多步精确预测。
1 灰色马尔可夫链预测理论
1.1 标准灰色预测理论
灰色系统理论以灰色系统为研究对象,可有效处理少数据、贫数据的不确定性问题,其中灰色预测理论是其研究的重点内容之一[7]。灰色预测方法是一种对含有不确定信息系统进行预测的方法,它介于白色预测和黑色预测之间,通过对杂乱无规律的原始数列进行累加,发现累加生成曲线是近似的指数增长曲线,而指数增长正好符合微分方程的形式,因此可通过构造核心灰色模型,对未来时刻的特征值进行外推预测[8-9]。灰色预测模型使用的不是原始时间序列,而是经过累加计算得到的生成序列,它具有较好的拟合和外推特性,建模所需数据较少,为及时体现数据的最新变化特征,建模所需样本数量一般在20个以下,最少仅需4个就可以建立灰色预测模型,适用于时间序列的中短期预测。随着样本数量的增加,预测计算量同步增加,而预测精度呈现先升后降的变化趋势,当样本数量选取过大时,经累加处理后,模型指数性变化特征将趋于固化,难以及时反映中短期数据的波动情况,降低模型预测精度。
灰色预测各主要环节的作用和计算过程[10-11]分别如下:1)原始序列级比检验,为保证时间序列具有适合灰色预测的分布规律,在进行灰色建模之前,需要对原始时间序列进行级比检验;2)一次累加生成序列,为降低原始数据的随机性,灰色预测常采用累加方法进行数据处理,得到建模所需的生成序列,具体规则为:将原始数据的第1个值作为生成序列的第1个值,后续数据逐步累加到前一个数据上,依次作为对应顺序的生成值;3)构造1阶微分方程,1阶生成序列具有近似指数增长趋势,可用1阶微分方程进行表示;4)建立灰色预测模型;5)数据预测与还原,这是由于直接预测的结果为累加形式,需要进行1阶累减运算进行还原。图1所示为灰色预测流程图。

图1 灰色预测流程图Fig.1 Flow chart of grey prediction
1.2 改进灰色预测理论
标准灰色负载功率预测模型完全基于历史功率数据拟合得到,没有考虑驾驶员操控指令对负载功率变化趋势的影响,而驾驶员的踏板操控指令会直接作用于车辆驱动系统中,从而对未来负载功率变化产生重要影响。这种影响在车辆油门踏板和制动踏板开度稳定不变或变化幅度较小时影响程度较低,但当驾驶员快速改变车辆油门踏板和制动踏板开度时,会造成车辆负载功率快速变化,极大降低基于历史功率预测模型的预测精度。因此,在标准灰色负载功率预测模型基础上,将驾驶员操控指令纳入负载功率预测中,对标准灰色负载功率预测模型进行改进,以提升复杂驾驶环境下的功率预测精度。
电传动装甲车辆的运动状态受到驾驶员意图的控制,当驾驶员踩下加速踏板时可以解析为增大驱动力,踩下制动踏板时可以解释为增大制动力。驾驶员的操控指令在车辆中的直观体现就是以轮毂驱动电机为主的负载功率调整,二者存在紧密联系。因此,以加速踏板和制动踏板为参考,构建驾驶员意图和负载功率的数学关系。
以标准灰色负载功率预测值为基准,假设驾驶员的踏板操控指令对未来负载功率变化趋势的影响以动态增益系数形式呈现[12]。
1.3 马尔可夫链预测理论
马尔可夫预测理论由俄国数学家马尔可夫于1906年提出,主要用于描述这样一种现象:事物的变化过程仅与当前时刻状态有关,而与事物的过去状态无关,上述过程称为马尔可夫过程[13-14]。马尔可夫方法是一种研究随机变化过程的方法,依据训练得到的状态转移概率矩阵,预测状态未来变化趋势。马尔可夫链是时间离散值的马尔可夫过程,它依据状态转移矩阵,对预测对象未来所处状态进行预测。此处以标准马尔可夫链为例,介绍其预测流程[15],如图2所示。

图2 马尔可夫链预测流程图Fig.2 Flow chart of Markov chain prediction
1.4 改进灰色马尔可夫链预测方法
基于改进灰色模型的功率预测方法能够对负载功率中的主体变化趋势进行较好的预测,但无法跟踪快速变化的功率分量,预测功率残差序列呈现平稳随机变化特点;马尔可夫链缺乏对带有连续性和因果性的负载主体功率进行预测的理论支撑,但擅长处理无后效性的时间序列预测问题。对于非平稳趋势性负载功率,单项预测方法均难以产生较为理想的预测效果[16]。理论和研究实践表明,在多个单项预测模型各异的情况下,组合预测方法能够发挥不同预测方法的优势,减少预测的系统误差,显著改进预测效果。


图3 改进灰色马尔可夫链预测流程图Fig.3 Flow chart of improved grey Markov chain prediction
2 负载需求功率组合预测方法
2.1 数据预处理
灰色预测是一种中短期预测方法,建立灰色预测模型不需要很多数据,一般只需要4个数据,就可以解决序列完整性和可靠性低的问题。电传动装甲车辆负载功率预测面向实时应用场景,历史数据较少,但对预测精度和在线计算速度要求较高,适用于采用灰色预测方法进行功率预测。灰色预测方法需要依托灰色预测模型进行计算,在灰色预测模型一次累加结构确定之后,建模历史数据的增加对预测精度的提升作用将逐渐趋于饱和,但计算量却呈现较快增长趋势。在满足数据趋势性预测前提下,为降低计算量,将灰色预测模型参考历史数据取为4个,设k时刻临近4个负载功率序列p(0)为
p(0)={p(0)(k-3),p(0)(k-2),
p(0)(k-1),p(0)(k)},k≥3.
(1)
定义负载功率序列最大值和最小值分别为

(2)

(3)
(4)
式中:c为平移变换因子;p(1)(h)为p(0)(h)平移变换后的功率序列,
p(1)(h)=p(0)(h)+c.
(5)
在负载功率极端取值情况下,确定平移因子的约束条件:

(6)

(7)
在可行域内,平移因子取值不宜过大,否则将弱化原始功率序列的变化特征。因此,平移因子取值应尽量靠近可行域下限,最终可取为

(8)
2.2 标准灰色预测模型
原始功率序列经过级比检验和平移处理后,保证了灰色模型的可行性,据此,可进一步开展后续建模工作。由于灰色模型中仅包含负载功率变量,应建立负载功率的灰色预测模型。
为消除满足级比功率序列的随机性,首先对原始功率序列进行一次累加运算,生成新的功率序列:
p(2)={p(2)(k-3),p(2)(k-2),
p(2)(k-1),p(2)(k)},
(9)
(10)
一次累加生成功率序列呈现单调增长的变化特征,曲线变化特征符合指数变化规律,可以用指数函数进行拟合。但是,单纯指数函数无法推导得到函数系数的最优解析解,而1阶微分方程的通解为指数表达形式,具有明确的代数表达形式,能够利用最小二乘法推导最优的解析解,因此采用1阶微分方程对生成功率序列进行拟合,设1阶微分方程表达式为

(11)
式中:a为增益参数;b为内生变量。
(11)式的通解表达形式为
(12)
式中:C为常数,由函数的初始条件决定,C∈R.
由于微分方程只适合连续可微函数,而功率序列离散非连续,对(11)式进行近似处理,得到的灰微分方程如(13)式所示:
p(2)(k)+ap(3)(k)=b,
(13)
式中:p(3)(k)为均值生成序列,
p(3)(k)=0.5p(2)(k)+0.5p(2)(k-1).
(14)
(10)式代入(13)式,可得
(15)
记
(16)
以拟合误差平方和J=(Y-Bu)T(Y-Bu)为优化函数,采用最小二乘法进行求解,得到使优化函数达到最小的u估计值为
(17)
(16)式代入(17)式,可得
(18)
在最小误差平方和意义下得到微分方程的最优系数估计值,代入(12)式中,得到一次累加生成序列的多步预测方程为
(19)
为将预测结果还原为满足级比检验的数据,再进行一次累减处理,得
(1)(k+i)=(2)(k+i)-(2)(k+i-1)=
(20)
为得到随机变化的功率数据,参照(5)式的平移变换过程,对(20)式进行反向平移变换,可得
(21)
据此,建立了标准灰色负载功率预测模型,可用于对负载功率进行多步预测。
2.3 改进灰色预测模型
以标准灰色负载功率预测值为基准,假设驾驶员的踏板操控指令对未来负载功率变化趋势的影响以动态增益系数形式呈现,则有
(4)(k+i)=(0)(k+i)κ(k,i).
(22)
指数预测是一种车辆控制领域最为常用的预测方式,广泛应用于车速预测、交通状况预测以及排放特性预测等方面,具有计算量小、短期预测迅速等特点。本节将驾驶员踏板开度对负载功率的短期影响视为指数变化趋势,则动态增益系数表达形式为
κ(k,i)=eλ(k)i,
(23)
式中:λ(k)为k时刻指数调整系数,取值范围为[-0.05,0.05]。
由于当前踏板开度仅可表示当前时刻状态,不具有预测功能,当前k时刻的踏板开度变化率作为自变量,其离散化计算公式为
(24)
式中:α(k)和α(k-1)分别为k和k-1时刻踏板开度;Ts为离散采样时间。
引入tanh 双曲正切函数,对具有数量级差异的变化率进行非线性尺度调整,将输入变量通过映射后,标准化到[-0.05,0.05]区间,以增强对不同采样时间的适用性,踏板开度变化率的处理过程为
(25)
式中:λ1(k)为k时刻指数调整系数。
为保证幅值相同但符号不同的指数调整系数具有相同的影响力,未来不同时刻负载功率的动态增益系数可设置为
(26)
(26)式代入(22)式,可得改进灰色负载功率预测模型为
(27)
2.4 马尔可夫链预测模型
马尔可夫链预测模型的核心在于状态转移矩阵的选取,传统马尔可夫链的状态转移矩阵多取为固定数值矩阵,它根据特定工况离线训练得到,适用于在固定工况下进行调用[18-20],但由于状态转移矩阵一经确定就不再变化,灵活性和自适应性较差,难以在工况多变的复杂场景下应用。而电传动装甲车辆驾驶工况和路面特征复杂多变,固定参数的状态转移矩阵无法表征多种工况,负载功率预测适用性和灵活性较差。为解决上述问题,将固定状态转移矩阵改进为自适应状态转移矩阵,通过设定滚动观测窗口,实时提取临近功率信息,自适应更新状态转移矩阵;同时,针对状态转移概率计算公式分母累加过大的问题,引入遗忘因子设定,在线迭代更新参考状态转移矩阵[21]。马尔可夫链模型建立步骤如下:
步骤1状态栅格化处理。
设残差功率范围为[Pmin,Pmax],根据预测精度要求,对论域进行栅格化处理,
(28)
式中:Sq为第q个栅格状态;r为栅格数量。
采用最近邻域法对n个残差功率进行分类[22],
(29)

步骤2滚动窗口状态转移矩阵计算。
截取临近w个样本历史数据,计算该窗口空间内由状态Sq转移到Sg的概率pqg,
(30)
式中:Mqg为由栅格状态Sq转移到Sg的次数。
因此,可得第i个窗口的一步状态转移矩阵Pi为
(31)
步骤3自适应更新状态转移矩阵。
为实现多场景在线应用,采用遗忘因子方法,对历史数据赋予不同权重系数,以消除数据饱和现象,加强当前数据的影响[23]。
采用线性递减方式,设置遗忘因子权重系数:
(32)
式中:ρi为第i个窗口状态转移矩阵权重系数;γ为历史窗口状态转移矩阵数量。
更新得到下一时刻状态转移矩阵估计值:
(33)
该状态转移矩阵估计值的展开式为
(34)
步骤4状态多步预测。
由柯尔莫格罗夫- 开普曼定理可知,功率预测中用到的多步状态转移矩阵可通过一步状态转移矩阵连乘实现[24]。若当前时刻的栅格状态为Si,根据多步状态转移矩阵估计值,可对未来时刻状态进行多步预测:
(35)

对栅格状态进行清晰化处理,可得
(36)
3 算例分析
3.1 仿真实验环境
实验用到的硬件在环仿真平台结构如图4所示。

图4 硬件在环仿真平台Fig.4 Hardware-in-loop simulation platform
该仿真平台主要由驾驶舱、数字信号处理(DSP)中央控制器、集成显示屏及实时仿真器RT-LAB组成,实现了集控制、电气、机械等多领域于一体的电传动车辆实时仿真功能。各类功率预测算法在dSAPCE实时仿真器的上位机中编写完成后,可以自动生成C代码,经编译后下载到实车DSP中央控制器中,2台RT-LAB实时仿真器分别运算综合电力系统和驱动电机的仿真模型,Vortex实时仿真系统中主要运行车辆动力学模型,上述各主要节点通过Flexray通信总线进行数据交互,在实验室环境下实现对实车控制系统结构和通信方式的高置信度仿真。
3.2 直线行驶功率预测实验
为检验改进灰色预测模型对负载功率的预测效果,依托硬件在环仿真平台进行实时仿真实验。仿真中设置车辆在水泥路面上直线行驶,初始时刻车辆处于静止状态,踏板开度为0%,转向开度为0%;实车控制器离散采样时间为0.002 s,灰色预测模型离散采样时间为1 s,预测时域长度为5 s,设置初始状态转移矩阵为15×15的单位矩阵 。硬件在环仿真中踏板操控指令、车速信息以及功率预测结果如图5~图10所示。

图5 实际车速曲线Fig.5 Actual speed curve

图6 踏板开度曲线Fig.6 Pedal opening curve

图7 多步保持模型预测功率Fig.7 Power predicted by multistep hold model

图8 标准灰色模型预测功率Fig.8 Power predicted by standard grey model

图9 改进灰色模型预测功率Fig.9 Power predicted by improved grey model

图10 改进灰色马尔可夫链模型预测功率Fig.10 Power prediced by improved grey Markov chain model
由于灰色模型的建立过程需要依托4个历史数据,而在最初时刻,灰色模型尚未建立起来,因此在最初的4 s内预测功率没有输出,在第5 s时刻,灰色马尔可夫链模型开始输出第1个预测数据,并在后续时刻每隔1 s的采样步长,分别对未来5步的功率进行同步预测。由图7可知,多步保持模型仅以当前时刻实际功率为参考,进行多步外推预测,没有考虑工况变化因素和驾驶员操控指令影响,预测方式简单,计算量较小,但在负载功率大小和方向实时变化的场景下,存在较大的预测误差;由图8和图9可知,标准灰色预测方法和改进灰色预测方法均可对未来负载功率进行多步预测,且预测精度随着预测时域的增加逐渐降低。其中,标准灰色模型完全基于历史功率数据训练得到,在短期功率变化相对稳定的情况下预测趋势与实际功率变化趋势一致性较高,但在功率频繁变化情况下,尤其是在驾驶员操控指令在加速和制动之间切换时,负载功率预测精度较低。改进灰色预测方法在标准灰色预测方法基础上,考虑了驾驶员操控指令对负载功率变化的影响,在加速和制动踏板变化较迅速时,能够及时修正预测方向,负载需求功率预测精度更高。由图10可知,改进灰色马尔可夫链预测方法对于未来负载功率具有多步预测能力,尤其在负载功率变化较为剧烈时,仍然具有较高的自适应能力和较高的预测精度,定性验证了改进灰色马尔可夫链预测方法的有效性。值得注意的是,在部分离散采样点,模型预测功率数值变化趋势与实际变化趋势吻合度较差,甚至出现预测反向的情况,这种情况主要出现在功率的转折变化时刻,此时灰色模型参数更新以及状态转移矩阵元素更新存在一定滞后,使得转折时刻预测趋势不能及时调整方向。为进一步展示不同时刻的预测效果,计算得到不同时刻的预测误差,分别如图11~图14所示。

图12 标准灰色模型预测误差Fig.12 Predicted error of standard grey model

图13 改进灰色模型预测功率Fig.13 Predicted error of improved grey model

图14 改进灰色马尔可夫链模型预测误差Fig.14 Predicted error of improved grey Markov chain model
为定量评价不同模型的功率预测效果,以预测的均方根误差作为模型在特定时刻预测效果的评价指标,并以5个时刻预测均方根误差的平均值作为模型整体预测效果的评价指标。均方根误差将每个预测值的误差以其误差的倍数进行放大,使得单个较大误差的预测值就能够使预测均方根误差增加很多[25]。具有较小预测均方根误差的方法所产生的预测误差一般较小,这正是高精度预测所追求的结果。因此,预测功率的均方根误差能较好地衡量预测的准确度。
不同预测方法下的负载功率预测均方根误差如表1所示。
由表1可知:多步保持模型在第1步具有较高的预测精度,但在未来第2到第5步的预测精度显著降低,且整体预测精度偏低,这是因为第1步时间较短,负载功率通常不会发生较大变化,但随着预测时间的延长,负载功率的变化趋势逐渐显现,且通常与当前时刻实际功率具有较大差距,因而造成了多步保持模型预测精度前高后低的效果;标准灰色模型考虑了历史功率的影响,从中拟合数据变化规律,相对于多步保持模型,除在第1步预测精度偏低外,后续多步预测精度均高于多步保持模型预测精度,预测效果提升约7.2%;改进灰色模型在标准灰色模型基础上,考虑了驾驶员操控指令因素的影响,在负载功率变化较为剧烈的时刻,能够预先对功率变化趋势进行判定,具有较高的预测精度,相对于多步保持模型,预测效果提升了10.41%;改进灰色马尔可夫链模型在改进灰色模型的基础上,采用马尔可夫链模型对预测残差功率进行了多步预测,以此为依据,对改进灰色模型预测结果进行修正,进一步提升了负载功率多步预测效果,其预测精度相对多步保持模型提升了14.26%,验证了负载功率预测方法的有效性。

表1 不同预测方法的定量评价指标(直线行驶工况)Tab.1 Quantitative evaluation indexes of different prediction methods (straight driving condition)
3.3 转向行驶功率预测实验
为检验负载需求功率预测方法在其他工况下的预测效果,设置车辆在砂石路面上转向行驶,初始条件设置与3.2节相同,仿真时间为90 s,记录得到仿真实验结果分别如图15~图21所示。

图15 实际车速曲线Fig.15 Actual speed curve

图16 踏板开度曲线Fig.16 Pedal opening curve
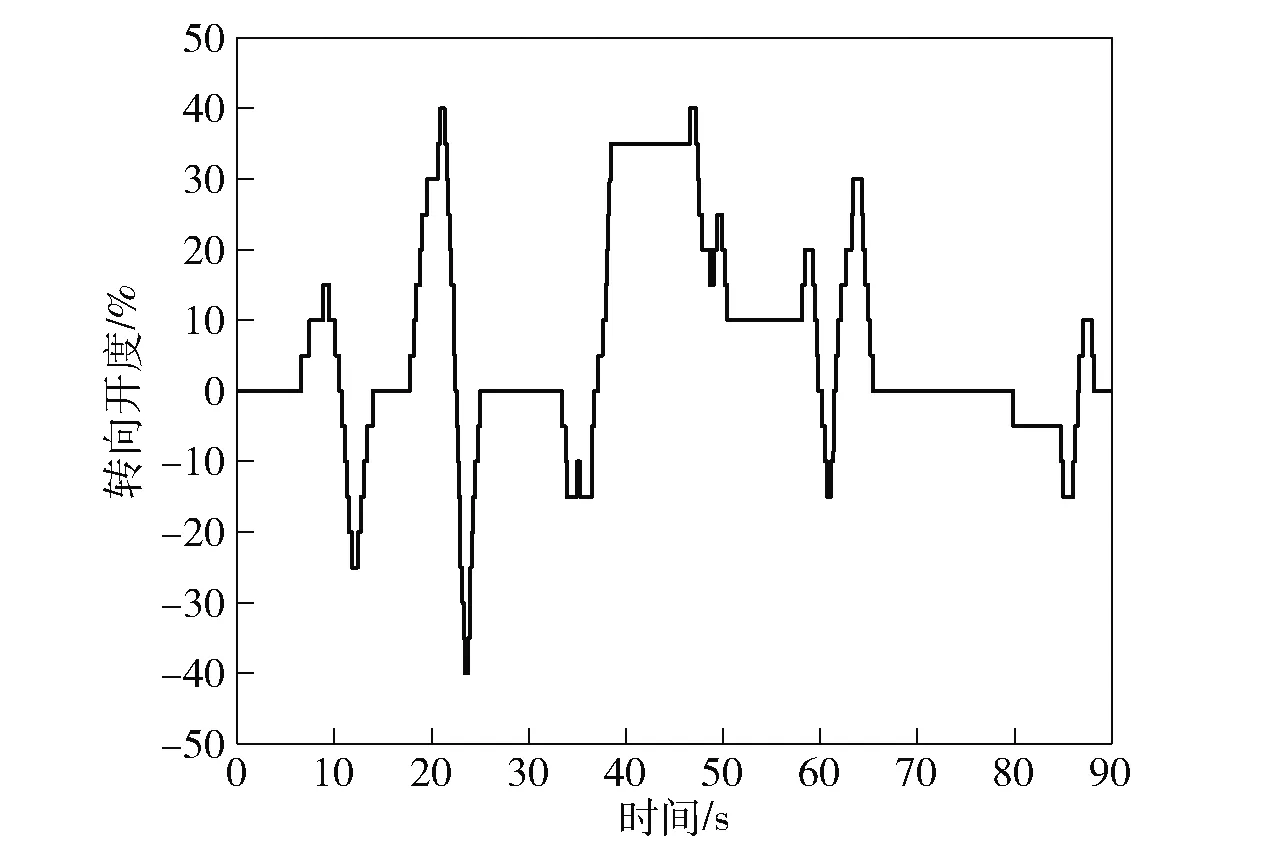
图17 转向开度曲线Fig.17 Steering opening curve

图18 多步保持模型预测功率Fig.18 Power predicted by multistep hold model

图19 标准灰色模型预测功率Fig.19 Power predicted by standard grey model

图20 改进灰色模型预测功率Fig.20 Power predicted by improved grey model

图21 改进灰色马尔可夫链模型预测功率Fig.21 Power predicted by improved grey Markov chain model
由图15~图17可知,驾驶员不断改变油门踏板和制动踏板开度及方向盘转向开度,车辆以中低车速转向行驶,使得车辆负载功率变化情况相较直线行驶更加复杂。由图18~图21可知,在不同负载功率预测方法下,功率预测效果存在较大差异。图18所示为多步保持模型的功率预测结果,未来5步预测功率值与当前采样时刻值始终保持一致,预测趋势不随踏板开度或转向开度变化,预测精度受到限制;图19所示为标准灰色模型的功率预测结果,未来功率预测趋势体现了短期历史功率数据的影响,相较多步保持模型预测方法,一定程度上提升了功率预测效果,但由于未考虑踏板开度等驾驶员操作指令的影响,预测精度提升幅度较低;图20所示为改进灰色模型功率预测结果,该方法考虑了驾驶员踏板开度和历史功率数据对未来功率变化的影响,未来5步预测功率与实际功率变化趋势较为接近,预测精度提升较为显著,但在功率转折时刻仍存在较大偏差;图21所示为改进灰色马尔可夫链模型预测结果,将预测残差功率无后效性的特点融入到预测建模过程中,在保持原有较高功率预测精度的前提下,进一步增强了功率转折时刻的预测精度,显著提升了复杂驾驶环境的功率预测效果。
分别记录未来5步各预测时刻的预测误差,结果如图22~图25所示。

图22 多步保持模型预测误差Fig.22 Predicted error of multi-step hold model
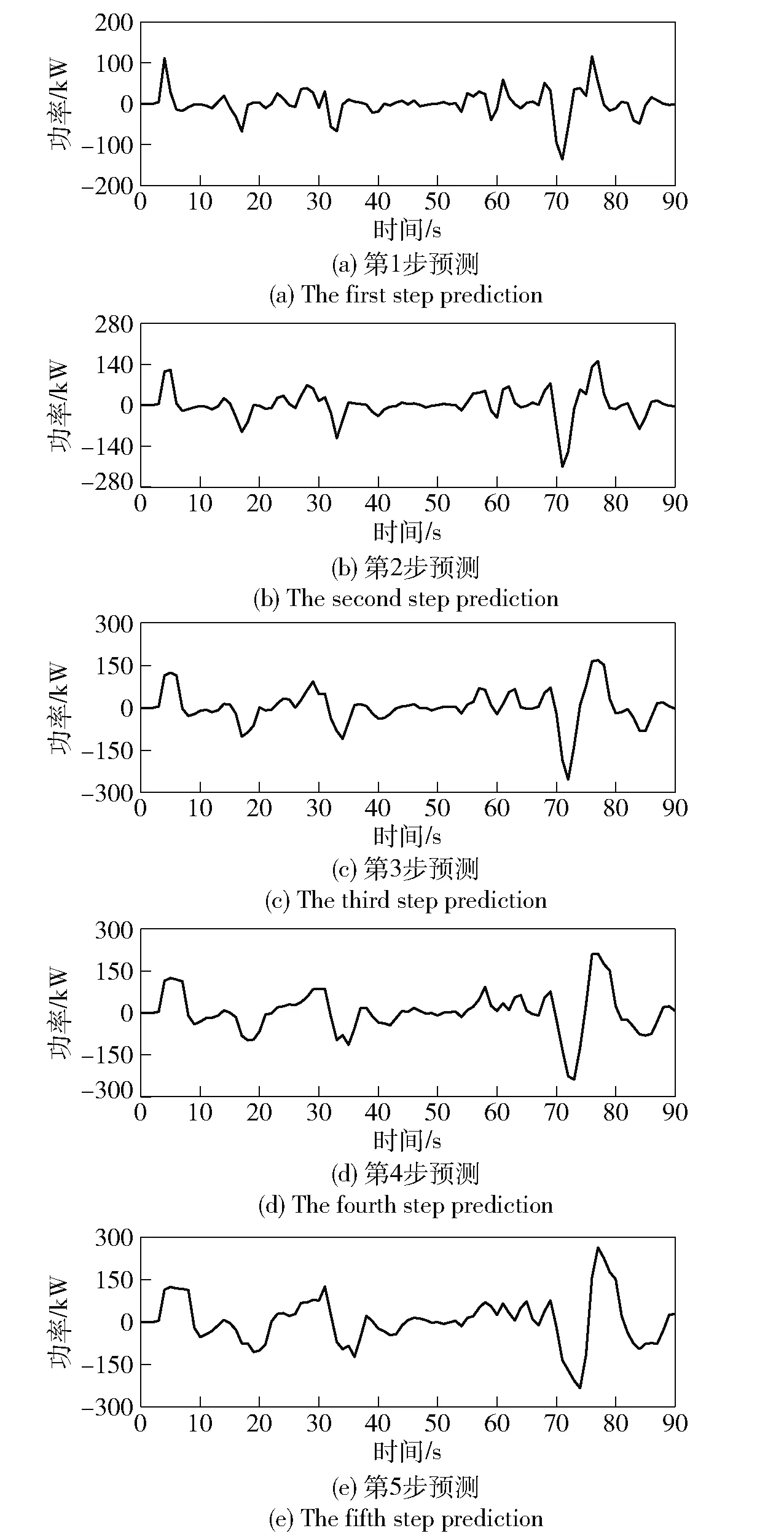
图23 标准灰色模型预测误差Fig.23 Predicted error of standard grey model

图24 改进灰色模型预测功率Fig.24 Predicted error of improved grey model
由图22~图25可知,随着预测步长的增加,预测误差呈现逐步增加趋势,但不同预测方法的预测误差大小存在一定差别。为定量评价不同预测方法的作用效果,根据记录的各步预测误差,计算得到不同预测方法下的均方根误差,结果如表2所示。
由表2可知:多步保持模型在第1步具有较高的预测精度,但在未来第2到第5步的预测精度显著降低,且整体预测精度偏低,这是由于第1步时间较短,负载功率通常不会发生较大变化,但随着预测时间的延长,负载功率的变化趋势逐渐显现,且通常与当前时刻实际功率具有较大差距,因而造成了多步保持模型预测精度前高后低的效果;标准灰色模型考虑了历史功率的影响,从中拟合数据变化规律,相较多步保持模型,除在第1步预测精度偏低外,后续多步预测精度均高于多步保持模型预测精度,预测效果提升约8.94%;改进灰色模型在标准灰色模型基础上,考虑了驾驶员操控指令因素的影响,在负载功率变化较为剧烈的时刻,能够预先对功率变化趋势进行判定,具有较高的预测精度,相较多步保持模型,预测效果提升了12.25%;改进灰色马尔可夫链模型在改进灰色模型的基础上,采用马尔可夫链模型对预测残差功率进行了多步预测,以此为依据,对改进灰色模型预测结果进行修正,进一步提升了负载功率多步预测效果,其预测精度相对多步保持模型提升了16.49%,验证了负载功率预测方法的有效性,能够为后续实时能量管理策略提供有效参考功率信息。

表2 不同预测方法的定量评价指标(转向行驶工况)Tab.2 Quantitative evaluation indexes of different prediction methods (steering driving condition)
4 结论
本文以电传动装甲车辆为研究对象,针对其需求功率呈现强随机性和多步预测困难等问题,采用改进灰色马尔可夫链组合预测方法,从历史功率数据中寻求内在变化规律,实现了对电传动装甲车辆负载需求功率的多步预测。得出以下主要结论:
1)电传动装甲车辆负载需求功率具有较强的随机性变化特征,传统单一预测方法难以实现多步精确预测,采用组合预测方法能够有效提升负载功率预测精度。
2)改进灰色马尔可夫链组合预测方法基于历史数据和驾驶员指令信息,可以实现对主体功率和残差功率的预测,完成对电传动装甲车辆负载需求功率的高精度预测。
3)未来负载需求功率是能量管理策略的重要参考输入信息,通过组合预测方法,实现功率预测时域和精度的同步增加,对于提升电传动装甲车辆能量管理控制效果将具有重要意义。

