车用双层内嵌式永磁同步电机转矩脉动抑制方法

孙承旭， 李琦， 范涛， 温旭辉， 李晔， 王艳艳， 谭平

(1.中国科学院 电工研究所， 北京 100190; 2.齐鲁中科电工先进电磁驱动技术研究院, 山东 济南 250100;3.江麓机电集团有限公司, 湖南 湘潭 411201)

0 引言

永磁电机以其高功率密度、高效率以及优良的动态性能，在车用电传动领域得到了广泛关注[1-4]。然而在实际的车用电传动应用中，永磁同步电机稳态运行时存在一定的转矩脉动，给驾驶员和乘员的舒适性带来负面影响，同时还会影响系统的控制精度，降低电驱动系统的可靠性和使用寿命。因此，转矩脉动成为衡量车用电传动电机性能的重要指标之一。针对永磁同步电机的转矩脉动削弱，国内外研究机构提出了许多切实可行的方法，主要分为以下两类：一类是从控制策略上对转矩脉动进行补偿[5-8]；另一类是从电机本体设计的角度出发，通过极槽配合选择、结构优化等手段降低转矩脉动[9-12]。

目前，由于双层内嵌式永磁体(IPM)转子结构能显著优化电机空载气隙磁密谐波，增加磁阻转矩与凸极效应，提升弱磁扩速能力，扩大恒功率运行范围，提高功率密度与转矩输出能力，近年来被广泛应用在车用电传动场合[13-15]。

相比采用有限元方法优化设计多层永磁转子，文献[16]采用解析磁路模型，将空载气隙磁密假设为双层阶梯梯形波，用以近似等效实际空载气隙磁密复杂的边缘波形，进一步提升了解析模型的计算精度，同时建立了多层永磁转子磁极参数与空载气隙磁密的关联，从而方便快速有针对性地进行转子磁极优化设计。

转子分段斜极技术是一种在工程实际中应用较为广泛的转矩脉动削弱方法。但实践经验表明，由于实际转矩波形的不对称性，转子分段斜极后，转矩谐波仍有较大残余。随着转子斜极段数增多，转矩脉动改善效果逐渐降低，但工艺难度及制造成本却逐渐增加。

本文在文献[16]基础上，针对一台车用电传动双层内嵌式永磁电机，采用解析法对其稳定运行时的转矩谐波进行分析，以揭示造成转矩脉动的谐波的主要特征阶次，并结合电磁有限元分析结果，验证解析推导的正确性。进一步，本文提出一种基于转矩波形对称性优化的转子两段斜极转矩脉动抑制方法。首先，在电机电磁性能不变前提下，以解析法为基础，提出一种通过优化双层内嵌式永磁电机转子磁极参数的方式，对转矩特定次谐波进行优化，以达到改善转矩波形对称性的目的。其次，在转矩波形对称性优化后的基础上，结合两段斜极的措施，对造成转矩脉动的转矩谐波进一步削弱。结果表明，本文提出方法有效降低了电机的转矩脉动。

1 转矩脉动分析

以一款电传动用永磁电机为基准，电机额定功率260 kW. 针对电机高额定效率的需求，采用双层内嵌式永磁转子增加磁阻转矩与凸极效应，提升弱磁扩速能力。电机定转子铁芯如图1所示。电机主要尺寸参数和指标如表1所示。

表1 基准电机主要尺寸参数和指标Tab.1 Main parameters and indexes of benchmark motor

图1 基准电机定转子铁芯Fig.1 Stator and rotor of benchmark motor

1.1 空载气隙磁密分析

图2所示为双层内嵌式永磁电机转子结构，主要由永磁体、磁障及隔磁磁桥三部分组成。图2中，p为电机极对数，b1、b2、b3分别为图2所示磁桥位置宽度，Wb,d为下层永磁体磁障厚度，Wb,u为上层永磁体磁障厚度，h1、h2、h3、h4、h5、h6、h7、h8分别为图2所示磁障位置宽度。

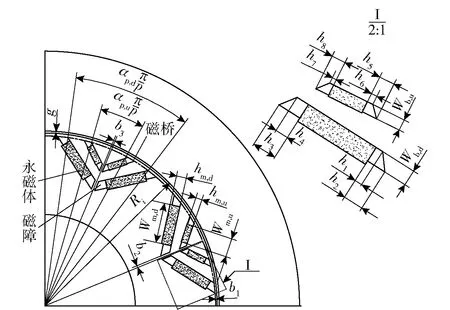
图2 转子结构示意图Fig.2 Structure of rotor

永磁电机的空载气隙磁密仅由永磁体产生，相邻磁极间构成闭合磁路，此时，实际电机中的闭合磁路示意图如图3所示，图中箭头方向为磁通流向。

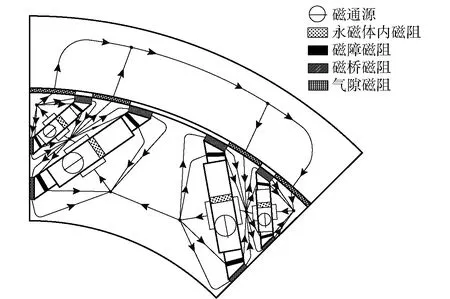
图3 空载磁路示意图Fig.3 Magnetic circuit under no-load condition

由于闭合磁路两侧是对称的，仅磁通流向相反，因此双层内嵌式永磁电机等效磁路可简化为如图4所示磁路模型[16]。

图4 双层内嵌式永磁电机等效磁路Fig.4 Equivalent magnetic circuit for double-layer IPM motor

图4中，Φr,d和Φr,u分别为下层永磁体和上层永磁体所产生的总磁通，Ro,d和Ro,u分别为下层永磁体和上层永磁体的总内磁阻，Rg,d为仅由下层永磁体产生磁通通过的气隙磁阻，Rg为上、下层永磁体产生磁通共同通过的气隙磁阻；Rb,d,b1为下层永磁体在尺寸为b1的隔磁磁桥处漏磁阻；Rb,d,b2为下层永磁体在尺寸为b2的隔磁磁桥处漏磁阻；Rb,u,b1为上层永磁体在尺寸为b1的隔磁磁桥处漏磁阻；Rb,u,b3为上层永磁体在尺寸为b3的隔磁磁桥处漏磁阻；Rl,d,L和Rl,d,R为下层永磁体两侧磁障处漏磁阻；Rl,u,L和Rl,u,R为上层永磁体两侧磁障处漏磁阻。

本文采用文献[16]所提出的双层内嵌式永磁电机空载气隙磁密等效模型，使用双层阶梯梯形波近似等效空载气隙磁密复杂的边缘波形。单极下空载气隙磁密波形等效为双层方波如图5(a)所示，等效为双层阶梯梯形波如图5(b)所示。图5中：B为磁感应强度，t为电机转子旋转时间；Ba,d为仅下层永磁体作用在气隙中的平均磁感应强度；Ba为上、下层永磁体共同作用在气隙中的平均磁感应强度；θe为0 s时刻与A相电枢绕组中心线的空间相对电角度；ωe为转子旋转的电角速度；θ′1和θ′2为空载气隙磁密等效为双层方波时，下层方波和上层方波直角边的空间电角度；θ1和θ2为空载气隙磁密等效为双层阶梯梯形波时，下层梯形波的下底边和上底边的空间电角度；θ3和θ4为空载气隙磁密等效为双层阶梯梯形波时，上层梯形波的下底边和上底边的空间电角度。

图5 双层内嵌式永磁电机空载气隙磁密等效波形Fig.5 Air-gap flux density distribution of double-layer IPM motor

由文献[16]的结论可知，将空载气隙磁密波形等效为双层阶梯梯形波更为接近空载气隙磁密实际波形，其前15阶谐波的总谐波失真与有限元计算结果的误差更小，计算精度更高，更有利于对空载气隙磁密谐波的准确分析。

假设初始时刻，电机转子磁极中心线与A相电枢绕组中心线对齐，根据图4所示等效磁路模型，结合磁路的基尔霍夫定律，可分别求取Ba,d和Ba[16].此时，图5(b)中双层内嵌式永磁电机空载时的气隙磁密可表示为

(1)

式中：Bg,μ为空载气隙磁密的第μ次谐波幅值，其表达式为

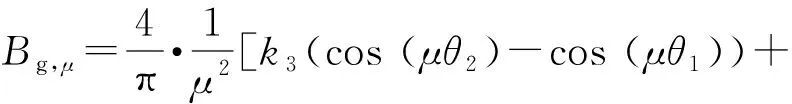
(2)

(3)

(4)

1.2 电枢反应气隙磁密分析

当气隙磁密仅由电枢反应产生时，假设基准电机通以三相对称正弦电流激励：

(5)

式中：iA(t)为A相电流激励；iB(t)为B相电流激励；iC(t)为C相电流激励；Im为电流幅值；φ为电流初相角。

以A相电枢绕组中心线为基准，可得三相绕组空间分布绕组函数[17]，如(6)式所示：

(6)

式中：NA(θe)为A相绕组空间分布绕组函数；NB(θe)为B相绕组空间分布绕组函数；NC(θe)为C相绕组空间分布绕组函数；h为绕组函数谐波次数；q为每极每相槽数；Nt为每槽导体数；a为电枢绕组并联支路数；kw,h为第h次谐波绕组系数。

由(5)式和(6)式可得三相绕组由电枢反应产生的气隙磁密为

(7)

式中：

(8)

μ0为真空磁导率。

1.3 转矩谐波分析

交流电机的转矩公式[18]为

(9)

式中：W′g为气隙内的磁共能；∂δ为转子虚位移。

当磁路不饱和时，气隙内的磁共能可表示为

(10)

式中：Wg为气隙内的磁能；V为气隙体积；b(θm,t)为气隙磁密表达式；θm为与θe对应的机械角度。

当气隙磁密由电枢反应和永磁体共同作用产生时，气隙磁密可表示为

b(θm,t)=ba(pθm,t)+bg(pθm,t).

(11)

联立(9)式、(10)式和(11)式，永磁电机转矩可表示为

(12)

式中：L为电机轴向有效长度。

由(1)式可知，永磁体产生的气隙磁密谐波次数μ为3、5、7、9等；由(7)式可知，电枢反应产生的气隙磁密谐波次数h为-5、7、-11、13等。因此，结合(12)式成立条件可知，永磁电机转矩谐波主要由永磁体产生的气隙磁密中5次和7次谐波，11次和13次谐波等形成的6及6的倍数次谐波构成，这是转矩脉动产生的主要原因。

2 转矩脉动成因及波形对称性优化

2.1 基准电机转矩脉动分析

采用有限元法对基准电机在额定工况下通以三相对称正弦激励电流时的转矩进行分析，转矩波形如图6所示，转矩波形频谱如图7所示。此时基准电机转矩谐波主要为6及6的倍数次，与解析所得结果一致。其中，6次及12次转矩谐波幅值最大，是基准电机转矩脉动的主要来源。图8所示为基准电机转矩6次谐波、12次谐波以及二者叠加后的波形。

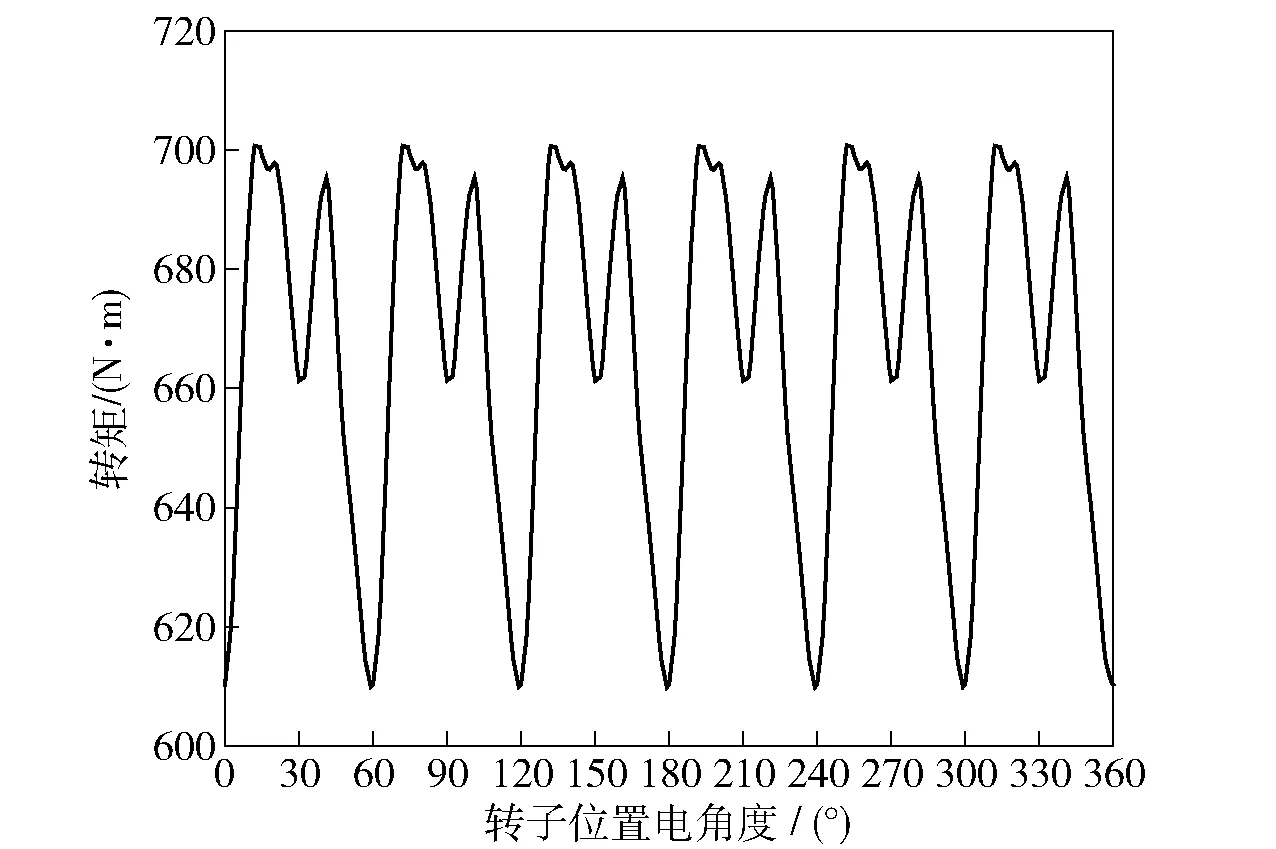
图6 基准电机转矩波形Fig.6 Torque waveform of benchmark motor

图7 基准电机转矩波形频谱分析Fig.7 Harmonic analysis of torque waveform

图8 基准电机主要转矩谐波波形Fig.8 Main torque harmonic waveforms of benchmark motor

由图8可见，基准电机转矩6次谐波和12次谐波叠加后的波形在一定程度上偏离6次或12次谐波的对称轴，这使得基准电机的转矩波形是非对称的。由于这种非对称性，导致在仅采用转子分段斜极的方法削弱电机转矩脉动时，仍然会有较大的残余。

以工程上常用的分段斜极方式对基准电机不同分段数下的转矩脉动和斜极系数进行分析，对比结果如图9所示。总斜极角度γP与转子分段数Nr之间的关系如(13)式所示：

(13)

式中：γτ为定子齿距角。

转子分段斜极后对反电势基波幅值的影响可用斜极系数表示，类比于绕组分布系数，斜极系数ks可定义为

(14)

式中：θs为相邻两段转子错开的电角度。

电机转矩脉动Tr定义为

(15)

式中：Tp为转矩峰- 峰值；Ta为转矩平均值。

图9的结果表明，随着分段数的增加，基准电机的转矩脉动虽然在逐步减小，但分段数超过3后削弱效果已经逐渐降低，工艺难度和制造成本不断增加。因此，结合实际的生产工艺水平，采用分段斜极的方法对电机转矩脉动进行抑制时，转子分段数不宜选择过多。

2.2 基准电机转矩波形对称性优化

2.1节中对基准电机额定运行时的转矩进行了分析，并对不同转子分段数斜极下的转矩脉动和斜极系数进行了比较，指出分段斜极抑制电机转矩脉动时，转子分段数不宜选择过多。因此本文选择采用两段斜极的方式对转矩脉动进行抑制。由图8可知，当转矩波形中只含有一种谐波时，即仅含有6次或仅含有12次谐波时，电机的转矩波形为理想的对称波形。此时，转子分为两段并斜过二分之一转矩谐波周期角度时，转矩谐波可完全抵消，如图10所示。

图10 理想对称转矩波形下两段斜极谐波波形Fig.10 Harmonics of double-segment rotor step-skewing in ideal symmetry torque waveform

显然，在采用转子分段斜极的方法削弱转矩脉动前，转矩波形的对称性越好，越有利于转矩脉动的优化。因此，为改善基准电机转矩波形的对称性，首先需要对6次或12次谐波进行抑制。本文选取对转矩的6次谐波进行抑制，转矩6次谐波的表达式为

(16)

空载工况下气隙磁密波形可等效为图5(b)所示的双层阶梯梯形波，在保证空载气隙磁密基波幅值Bg,1和总磁通不变情况下，以(16)式为基础，改变极弧系数αp,d和αp,u，以转矩6次谐波幅值最小为目标对基准电机转子磁极极弧系数组合进行寻优。

图11、图12所示为不同极弧系数组合下的转矩6次谐波幅值标幺后的分布情况。可见使转矩6次谐波幅值最小的极弧系数组合为αp,d=0.73,αp,u=0.36.

图11 不同极弧系数组合下转矩6次谐波分布情况Fig.11 Distribution of 6th order torque harmonics with different pole arc combination

图12 优化前后不同极弧系数组合下转矩6次谐波分布情况(图中数值为转矩6次谐波幅值的标幺值)Fig.12 Contour of 6th order torque harmonics with different pole arc combinations before and after optimization (the numerical values are the amplitudes of 6th order harmoinics after per-unit processing)

3 仿真验证及结果分析

3.1 转矩波形对称性优化仿真验证

为验证解析法优化转矩波形对称性的有效性，本文根据优化后极弧系数建立了有限元模型，并对优化后不考虑斜极时的电机转矩进行了分析。优化前后电机空载气隙磁密空间分布波形对比如图13所示，优化前电机空载气隙磁密基波幅值为1.083 7 T，优化后电机空载气隙磁密基波幅值为1.085 0 T.

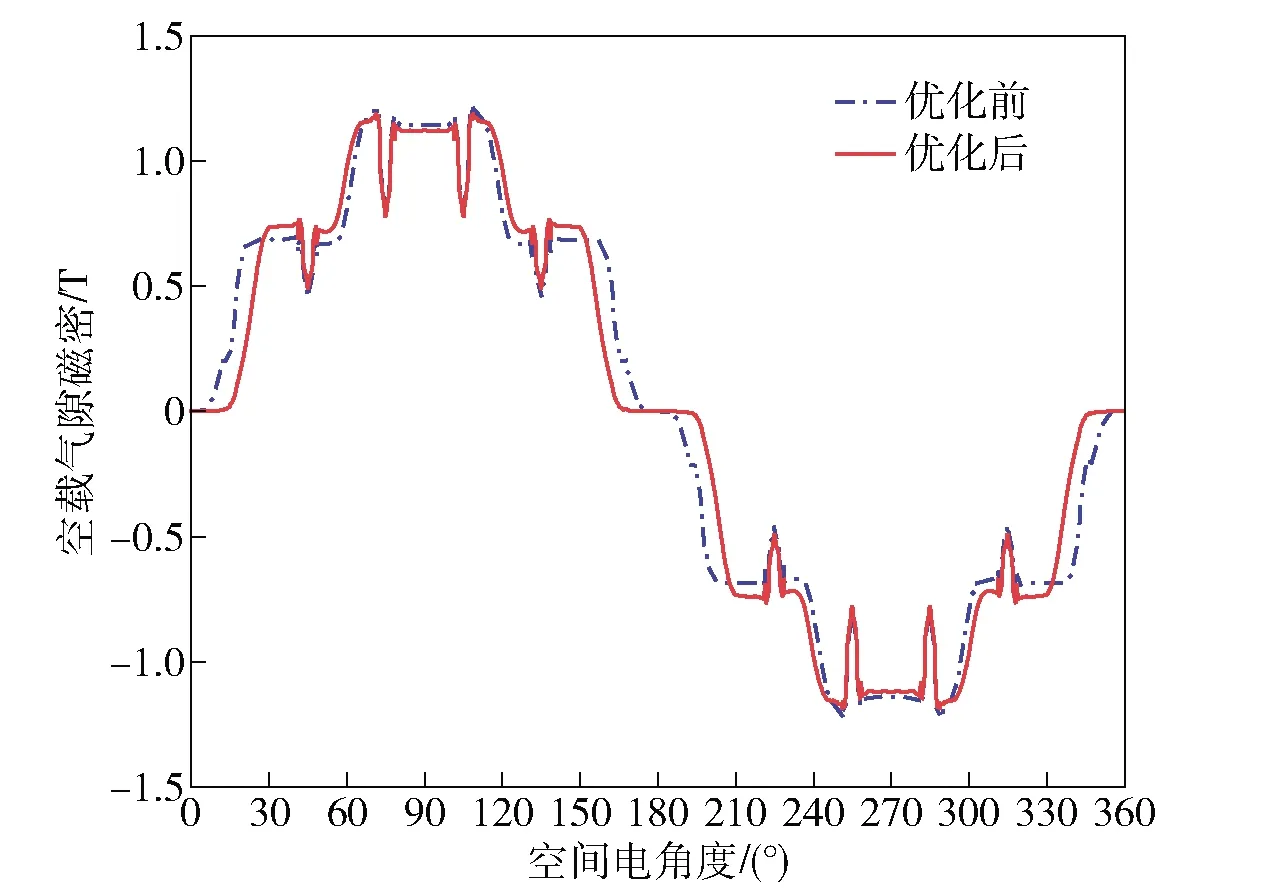
图13 优化前后电机空载气隙磁密空间分布Fig.13 Comparsion of air-gap flux densities before and after optimization

图14所示为优化后电机不考虑转子分段斜极时转矩波形。图15所示为优化后电机不考虑转子分段斜极时转矩6次谐波、12次谐波以及二者叠加后的波形。

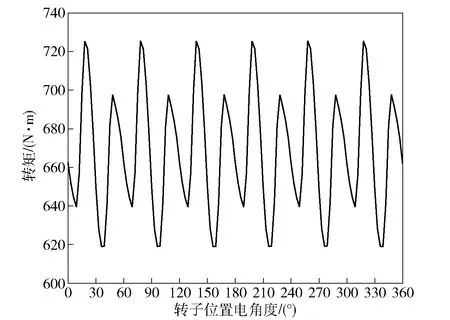
图14 优化后电机转矩波形(未分段)Fig.14 Torque waveform of motor after optimization (before rotor step-skewing)

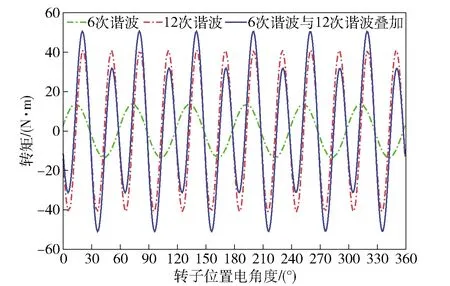
图15 优化后电机主要转矩谐波波形(未分段)Fig.15 Main torque harmonic waveforms of motor after optimization (before rotor step-skewing)

表2所示为优化前后不考虑转子分段斜极主要转矩谐波幅值对比。

图14、图15和表2的结果表明，不考虑转子分段斜极时的转矩6次谐波明显降低，转矩波形对称性优化后的电机转矩6次谐波为13.63 N·m，较优化前降低了54.9%，此时转矩12次谐波成为转矩脉动的主要谐波成分。表明转矩波形对称性得到了明显提升，验证了转矩波形对称性优化的有效性。

表2 优化前后主要转矩谐波幅值对比Tab.2 Comparison of main orders amplitudes of torque harmonics before and after optimization

3.2 分段斜极优化转矩脉动仿真验证

针对转矩波形对称性优化后的电机，再结合两段转子斜极的方式，对12次转矩谐波进行削弱。此时，两段转子间的斜极角度应为2.5°. 两段斜极后的电机转矩波形如图16所示，转矩波形频谱如图17所示。由图16和图17可见，电机转矩波形对称性优化后，再采用两段斜极的方法，转矩12次谐波被有效抑制，转矩脉动得到了有效改善。

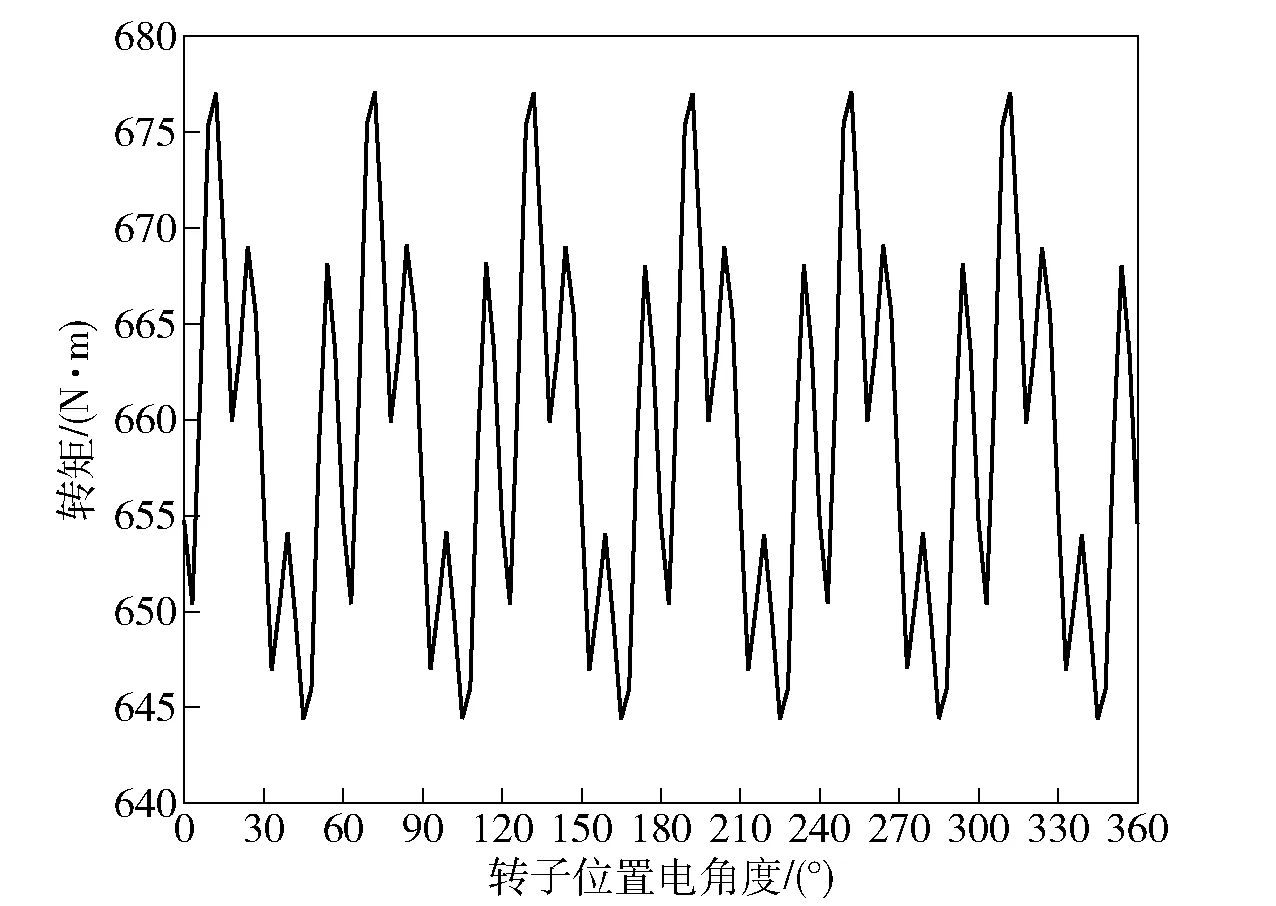
图16 优化后电机转矩波形(两段斜极后)Fig.16 Torque waveform of motor after optimization (after double-segment rotor step-skewing)

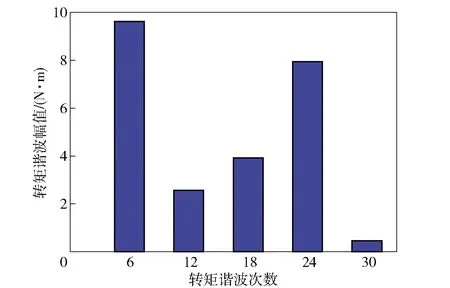
图17 优化后电机转矩波形频谱分析(两段斜极后)Fig.17 Harmonic analysis of torque waveform after optimization (after double-segment rotor step-skewing)

两段斜极后电机与基准电机的性能对比如表3所示。

表3 优化前后电机电磁性能对比Tab.3 Comparison of electromagnetic properties of initial and optimized motors

以上分析结果表明，电机优化前后基本性能保持不变，转矩脉动相比于基准电机降低了63.5%，得到有效抑制。采用转矩波形对称性优化并结合两段斜极方式抑制后的转矩脉动，相比于基准电机单纯采用多段斜极方法时的转矩脉动最小值，降低了22.3%. 进一步验证了本文提出的转矩脉动抑制方法的有效性。

4 结论

本文针对一台采用双层内嵌式永磁转子结构的电传动用永磁同步电机，以磁路解析模型为基础，对其稳定运行时的转矩谐波构成进行系统分析，并提出了一种基于转矩波形对称性优化的转子两段斜极转矩脉动抑制方法。得出主要结论如下：

1)造成电机转矩脉动的转矩谐波主要特征阶次为6及6的倍数次，电磁有限元分析结果验证了磁路解析模型的正确性。

2)采用转子分段斜极方法削弱转矩脉动前，转矩波形的对称性越好，越有利于转矩脉动的优化。利用解析法，优化双层内嵌式永磁电机转子磁极参数，对转矩6次谐波进行抑制，转矩6次谐波降低54.9%，转矩波形对称性明显提升。

3)转矩波形对称性优化后，结合两段转子斜极措施削弱造成转矩脉动的12次转矩谐波，转矩脉动相比于基准电机降低63.5%，相比于基准电机单纯采用分段斜极方法时的转矩脉动最小值降低22.3%.

4)相比于单纯采用转子分段技术抑制转矩脉动，本文提出方法具有制造工艺性好、生产成本低、质量一致性容易保证的优势，在实际的电机设计及生产过程中具有一定的参考意义。