永磁同步电机静止参数辨识及电流环控制器自动参数整定

孟柳， 章回炫，2， 范涛，2

(1.中国科学院 电工研究所， 北京 100190； 2.中国科学院大学， 北京 100049)

0 引言

永磁同步电机因其高功率密度、高效率、高可靠性和宽调速范围等优点，已经广泛应用于伺服系统、航空航天及电动汽车等领域。工程中常用的控制方法是基于数字PI控制器的双闭环矢量控制系统，其中电流环作为控制系统的最内环是整个控制系统的基础。

一般情况下，控制系统在匹配新的电机平台时需要进行控制器参数的调节，使电机平台能够顺利启动并初步达到稳定运行的能力，在此基础上再进行后续功能的开发及优化。此过程可以称之为控制系统的初始化过程，通常情况下该项工作需要有经验的工程师进行人工调节，尤其是当电机参数未知时，该过程可能需要工程师花费更多的时间和精力。

由于电流环控制器的控制参数主要依赖于电机参数，辨识出电机参数后结合电流环控制器参数整定方法可以实现控制器参数的自动整定。由此不仅可以节省控制系统的初始化时间，还能使控制系统在匹配不同电机平台时都能具有良好的控制性能[1-4]。因此对电机进行初始参数辨识显得尤为重要。

电流环设计用到的主要电机参数包括定子电阻和交直轴电感。定子电阻的传统测量方法包括交流静态法、直流暂态法、直接负载法等，这些方法通常需要借助电桥等外部仪器或电路进行人工电阻测量[5-6]，同时对实验人员也有一定要求，不利于提高系统的通用性及辨识效率。与此相比采用伏安法辨识电阻的实现过程较为简单方便，只需向转子方向注入一定幅值的电压，等待电流稳定后即可计算出定子电阻值[7]。但由于注入的电压值较小，受死区影响较大，因此本文采用两点式伏安法辨识电阻消除了死区带来的影响，提高了辨识精度[8-9]。

交直轴电感辨识常用的方法是电压阶跃响应法及高频注入法，其中电压阶跃响应法需要分别向交直轴方向注入恒定的电压，检测电流上升过程，此方法在辨识过程中可能会引起电机转动，且电感的辨识结果受电阻值影响会将电阻辨识结果中的误差带入电感值中[10-12]。本文采用的高频注入法由于注入的电压信号频率较高，且其电压平均值为0 V，不会引起转子转动，结合离散傅里叶变换检测电流幅值来计算电感值，使辨识算法较为简单易于实现[8，13-14]。

对于电流环控制器参数整定的方法，本文阐述了基于电流环零极点相消的控制器参数整定方法[15-18]。该方法在获得电机参数后，结合设定的期望开环截止频率即可实现控制器参数的自动整定。最后，通过实验验证了本文方法的有效性及通用性。

1 永磁同步电机静止参数辨识

1.1 定子电阻辨识

对永磁同步电机定子电阻辨识采用的是两点式伏安法。电机的直轴电压方程为

(1)

式中：Ud为直轴d电压幅值；R为定子电阻；id、iq分别为直轴d、交轴q的电流幅值；Ld、Lq分别为直轴、交轴电感值；ωe为同步角速度。

采用伏安法辨识电阻时，是对永磁同步电机的三相绕组施加一个较低的直流脉冲电压，当注入电压方向与电机直轴方向相同时，电机中不会产生旋转磁场，转子不会发生转动，也不会产生反电动势，此时的直轴电压方程可以表示为

(2)

受系统中电感的作用三相电流会经过一段时间后达到一个稳定值，当响应电流稳定后，根据指令电压值和响应电流值可以得到电阻的辨识值。

图1所示为静止参数辨识原理框图，其中虚线区域为定子电阻辨识部分。图1中，Uq为交轴电压幅值；dq表示两相旋转坐标系；αβ表示两相静止坐标系；SVPWM表示空间矢量脉宽调制；abc表示三相静止坐标系；ia、ib、ic为三相交流电流幅值。

实验中给定一个恒定的直流电压UDC，令Ud=UDC，等待电流稳定后记录响应电流稳态值idf，由此定子电阻可以表示为

(3)

由于逆变器无法提供恒定的直流电压，实际是通过给定恒定占空比对母线电压进行高频斩波获得的等效直流电压。永磁同步电机定子电阻一般较小，为了避免产生过大电流，通常所需的直流电压值较小，而直流母线电压较高，脉冲宽度调制(PWM)信号的占空比很小，此时由于死区时间带来的影响较为明显。

受死区影响，逆变器实际输出电压与期望输出电压之间存在一个误差Δu，由于输出电压是直流且稳定情况下系统模型是线性的，误差电压Δu可以认为是一个恒定值，因此采用两点式伏安法辨识电阻值为

(4)

式中：UDC1、UDC2分别为直轴注入的两次直流电压指令值；idf1、idf2分别为两次直轴响应的电流值；Ud1、Ud2分别为两次直轴注入的实际直流电压幅值。

由(4)式可知，通过注入两个幅值不等的直流电压，根据电压差值和响应电流的差值来辨识电阻，可以消除死区对辨识结果的影响。

伏安法辨识电阻时系统是开环状态且注入的电压为脉冲电压，考虑到不同的电机电阻值不同，注入同一个电压值得到的响应电流值也不同，过大的电流值可能对控制器及电机造成伤害，而过小的电流值可能影响辨识精度。因此本文为了提高系统的通用性及辨识效率，根据响应电流的实时值自动调整注入的电压值，确保最终辨识电阻时所用的响应电流值在一个合理的范围，辨识流程如图2所示，初始给定的两个电压指令中第1个电压指令大于第2个电压指令。图2中USD、USI分别表示电压指令减小和电压指令增大步长，Idmax、Idmin分别表示设定得电流上限值和电流下限值。

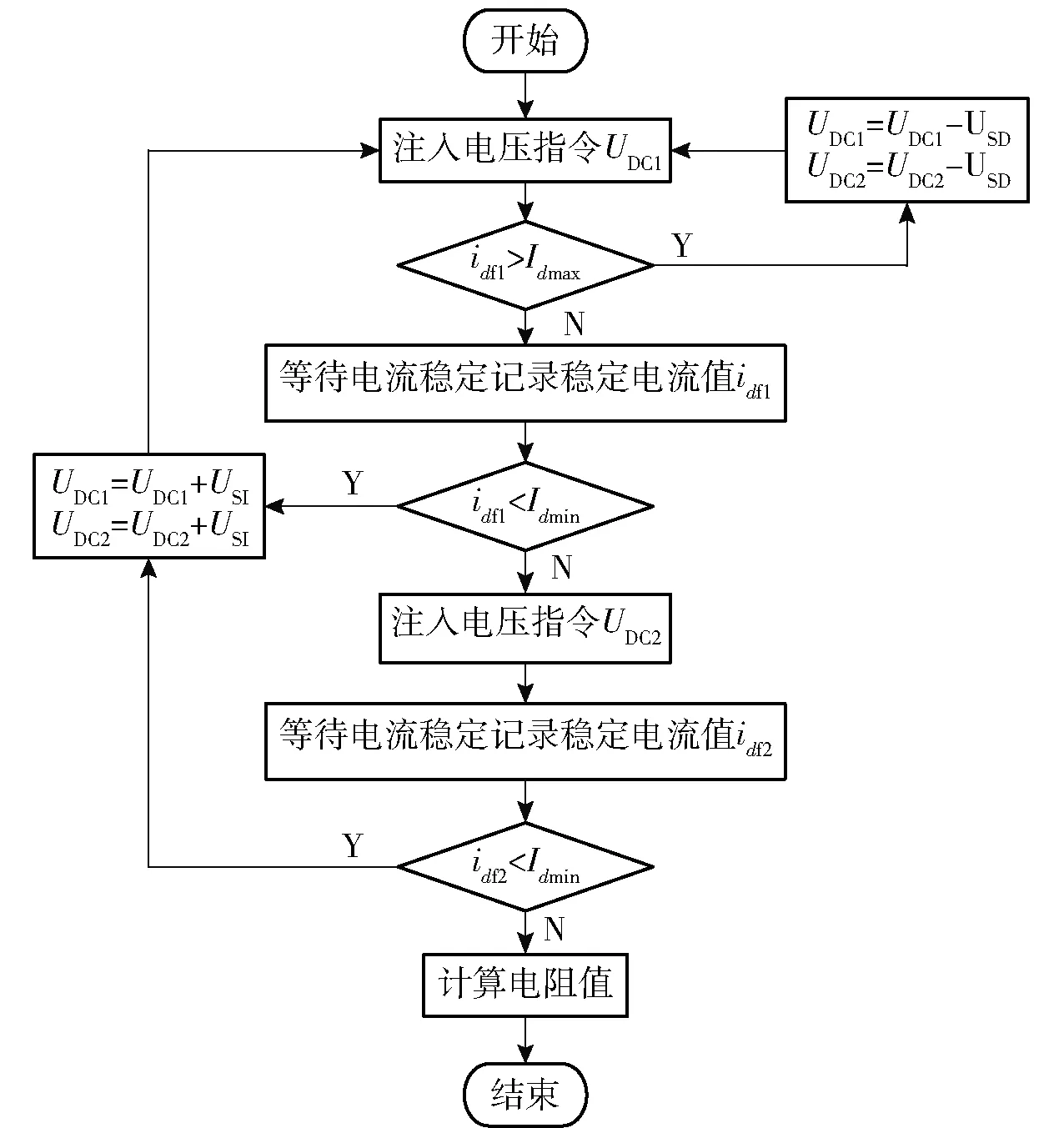
图2 定子电阻辨识流程图Fig.2 Flow chart of stator resistance identification

1.2 等效电感辨识

本文采用高频注入法辨识永磁同步电机的交直轴等效电感。辨识过程中分别向电机的交直轴注入高频电压信号，根据注入电压的幅值、频率和响应的电流幅值来辨识相应的电感值。永磁同步电机在两相旋转坐标系下的电压方程为

(5)

式中：ψf为永磁体磁链。

由于注入的高频信号频率较高且电流均值为0 A，辨识过程中电机保持静止，考虑到电阻项很小，在此可以忽略不记，因此电压方程可以简化为

(6)

以直轴为例，注入如下形式的高频电压信号

(7)

式中：Udh、ωdh分别为直轴注入高频电压信号的幅值和频率。得到的响应电流为

(8)

式中：Idh为直轴响应电流的幅值。

如图1中点横线区域为电感辨识部分，根据电压方程表达式，已知注入的电压幅值及频率只需获得响应的交流电流幅值即可直接计算电感值，由此直轴电感表达式为

(9)

同理，交轴电感表达式为

(10)

式中：Uqh、ωqh分别为交轴注入高频电压信号的幅值和频率；Iqh为交轴响应电流的幅值。

考虑到采样得到的电流值为离散量，本文采用离散傅里叶变换求得电流信号的基波幅值，对电流的一个周期进行N次采样，根据(11)式计算基波电流信号的实部a1和虚部b1，再通过(12)式来计算电流幅值M.

(11)

(12)

交轴电感的辨识流程与直轴类似，在交轴注入高频电压信号，根据离散傅里叶变换求得响应电流的基波幅值，再根据注入频率及电压和电流的幅值计算交轴电感值。

2 永磁同步电机电流环自动参数整定

2.1 电流环数学模型

永磁同步电机电流环系统通常包括电流环控制器、逆变器、电机模型以及电流滤波器。其中电流环控制器一般采用PI控制器，其传递函数为

(13)

式中：Kp为PI调节器的比例增益；Ti为积分时间常数；s为拉普拉斯算子。在工程设计中通常将PI控制器表达式等效为

(14)

式中：Ki为积分增益系数，Ki=Kp/Ti.

对逆变器环节作1阶惯性环节与比例环节直接串联处理，其传递函数为

(15)

式中：KPWM为逆变器的放大倍数，其定义为实际输出电压与给定电压的比值，当前的数字控制系统中通常采用SVPWM控制，逆变器输出电压与给定电压相等，故KPWM=1；TPWM为逆变器的控制周期。

根据(5)式所示电压方程，以交轴为例，永磁同步电机的传递函数为

(16)

为了提高系统的控制性能，电流环中的电流反馈还会经过一个滤波环节，滤波器的传递函数为

(17)

式中：Tcf为电流反馈滤波时间常数。

综上所述，永磁同步电机的电流环控制结构框图如图3所示。图3中，iq,r为交轴电流指令值。

图3 永磁同步电机电流环控制结构框图Fig.3 Block diagram of PMSM current loop control structure

此时系统的开环传递函数为

(18)

2.2 电流环控制器参数整定

由电流环开环传递函数表达式可知，当ω为开环截止频率ωc时，得

|Gcl(jωc)|=1,

(19)

式中：j为虚数。

由于系统中1/TPWM和1/Tcf的值远大于电流环的开环截止频率，故电流环中的逆变器和电流滤波器对系统中、低频段响应特性的影响可以忽略不计，此时电流环的开环传递函数可以简化为

(20)

电流环作为永磁同步电机控制系统的最内环，其控制性能直接影响系统最终的控制效果，为保证永磁同步电机的动态和静态性能，要求电流环在稳态时保证无静差，动态时对电流指令具有良好的响应速度。根据自动控制系统，典型Ⅰ型系统只要参数的选择能保证足够的中频带宽度，系统就一定是稳定的，且有足够的稳定裕量。同时由于电机的电气时间常数Tl=Lq/R通常较大，为了尽可能削弱大惯性环节对系统的影响，提高系统的动态响应速度，在工程设计中，通常用电流环控制器的零点对消掉被控对象中较大时间常数的极点，将电流环开环传递函数校正成典型Ⅰ型系统，则

(21)

再根据(19)式得到电流环控制器参数为

Kp=Lqωc,
Ki=Rωc.

(22)

由(22)式可知，已知电机参数后，只需要根据系统要求设定系统期望开环截止频率，即可实现电流环控制器参数的自动整定。

工程中通常取系统闭环带宽ωb近似为开环截止频率的1.1～1.4倍，同时为避免逆变器开关谐波对系统产生干扰，电流环的闭环带宽要小于系统开关频率的1/10[15]，因此

(23)

(24)

3 实验结果

为了验证本文控制算法的有效性及通用性，分别在两组不同的永磁同步电机平台上进行实验验证。图4和图5所示为25 kW永磁同步电机实验平台和20 kW永磁同步电机实验平台。两组实验平台均包括2台对拖的永磁同步电机，其中一台控制系统转速，一台控制系统转矩。

图4 25 kW永磁同步电机实验平台Fig.4 Experimental platform of 25 kW PMSM

图5 20 kW永磁同步电机实验平台Fig.5 Experimental platform of 20 kW PMSM

在两组实验平台上进行实验时，均将其中控制系统转矩的永磁同步电机作为被辨识和控制的对象。2台被辨识的电机参数分别如表1和表2所示，其中电机的定子电阻和交直轴电感值为电机的设计值，可作为辨识结果的参考，实验时系统的开关频率均为10 kHz.

表1 25 kW永磁同步电机参数表Tab.1 Parameters of 25 kW PMSM

表2 20 kW永磁同步电机参数表Tab.2 Parameters of 20 kW PMSM

首先在25 kW永磁同步电机实验平台上进行实验，先对电机的定子电阻进行辨识，整个辨识时间大致为2.5 s. 如图6(a)所示，实验中分别向直轴施加两次幅值不等的电压信号，初次给定电压信号UDC1=3.5 V，第2次给定的电压信号UDC2=3 V，两次注入电压持续时间均为0.3 s. 图6(b)为响应电流波形，等待电流值趋于稳定后，分别测量并记录两次电流幅值。如图7所示，根据两次注入的电压值和响应电流稳态幅值计算得被辨识电机电阻值为6.2 mΩ.

图6 25 kW永磁同步电机实验平台上辨识定子电阻时直轴电压和电流波形Fig.6 Direct-axis voltage and current waveforms for stator resistance identification on 25 kW PMSM experimental platform

图7 25 kW永磁同步电机实验平台上定子电阻辨识结果Fig.7 Identified results of stator resistance on 25 kW PMSM experimental platform

辨识等效交直轴电感时，分别向直轴和交轴方向注入高频电压信号。实验中注入电压信号的频率均为250 Hz，注入信号持续时间均为0.5 s，辨识直轴电感值时注入的电压信号幅值为20 V，辨识交轴电感值时注入的电压信号幅值为40 V. 图8为辨识直轴电感时向直轴注入的正弦电压波形和响应电流波形，辨识得到的直轴电感值为119 μH(见图9)；图10为辨识交轴电感时向交轴注入的正弦电压波形和响应电流波形，辨识得到的交轴电感值为394 μH(见图11)。

图8 25 kW永磁同步电机实验平台上辨识直轴电感时电压和电流波形Fig.8 Voltage and current waveforms for direct-axis inductance identification on 25 kW PMSM experimental platform

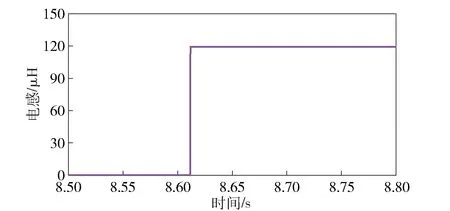
图9 25 kW永磁同步电机实验平台上直轴电感辨识结果Fig.9 Identified results of direct-axis inductance on 25 kW PMSM experimental platform

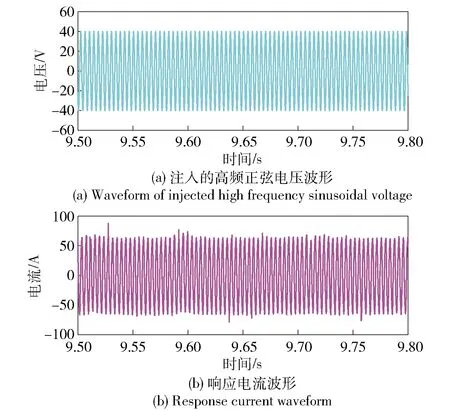
图10 25 kW永磁同步电机实验平台上辨识交轴电感时电压和电流波形Fig.10 Voltage and current waveforms for quadrature-axis inductance identification on 25 kW PMSM experimental platform

图11 25 kW永磁同步电机实验平台上交轴电感辨识结果Fig.11 Identified results of quadrature-axis inductance on 25 kW PMSM experimental platform

实验中为了增加辨识结果的准确性，通过离散傅里叶变换计算电流幅值时，随机选取4个电流周期分别计算电流幅值，再对这4个电流幅值求平均后，结合注入电压信号幅值及注入信号频率计算电感值。

在辨识得到电机的定子电阻和交直轴电感值后，采用电流环控制器参数整定方法对电流环所用PI控制器参数进行自动整定，为保证系统的稳定性，设置电流环系统的期望截止频率为200 Hz，结合辨识结果计算得到控制器参数Kp=0.32，Ki=7.75，这里用到的电感值为平均电感值。

图12所示为25 kW永磁同步电机运行于500 r/min时阶跃给定交轴电流指令50 A的电流响应波形，根据波形图可以看到响应电流的响应速度较快且基本无超调，响应值与指令值之间无静差。

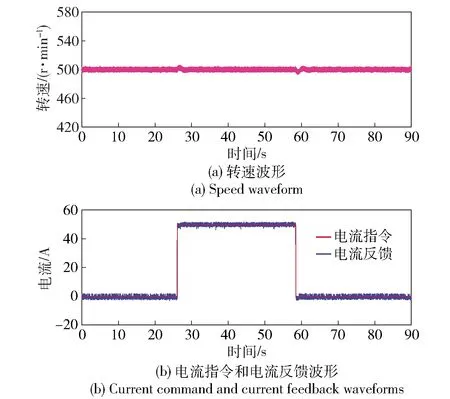
图12 25 kW永磁同步电机实验平台上交轴电流阶跃响应波形Fig.12 Quadrature-axis current step response waveform on 25 kW PMSM experimental platform

在20 kW永磁同步电机实验平台上进行重复实验，同样先进行定子电阻辨识。如图13所示，实验中初次给定电压信号UDC1=6.5 V，第2次给定的电压信号UDC2=6 V，两次注入电压持续时间均为3 s，辨识结果如图14所示，计算得到被辨识电机电阻值为13.2 mΩ.

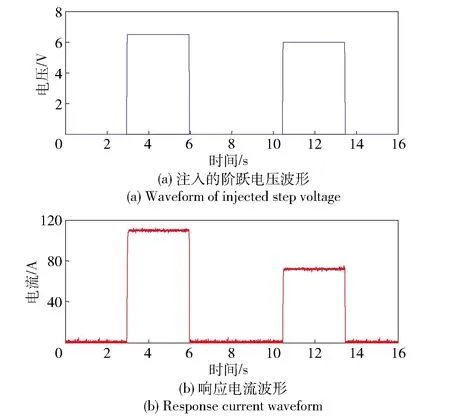
图13 20 kW永磁同步电机实验平台上辨识定子电阻时直轴电压和电流波形Fig.13 Voltage and current waveforms for stator resistance identification on 20 kW PMSM experimental platform

图14 20 kW永磁同步电机实验平台上定子电阻辨识结果Fig.14 Identified results of stator resistance on 20 kW PMSM experimental platform

图15～图18为辨识等效交直轴电感的实验波形。实验中注入电压信号幅值与频率均与25 kW永磁同步电机实验平台的实验相同，但由于两台被测电机的电感值不同，其对应的高频响应电流幅值也不同，计算可得20 kW永磁同步电机的交直轴电感辨识结果分别为170 μH和250 μH.

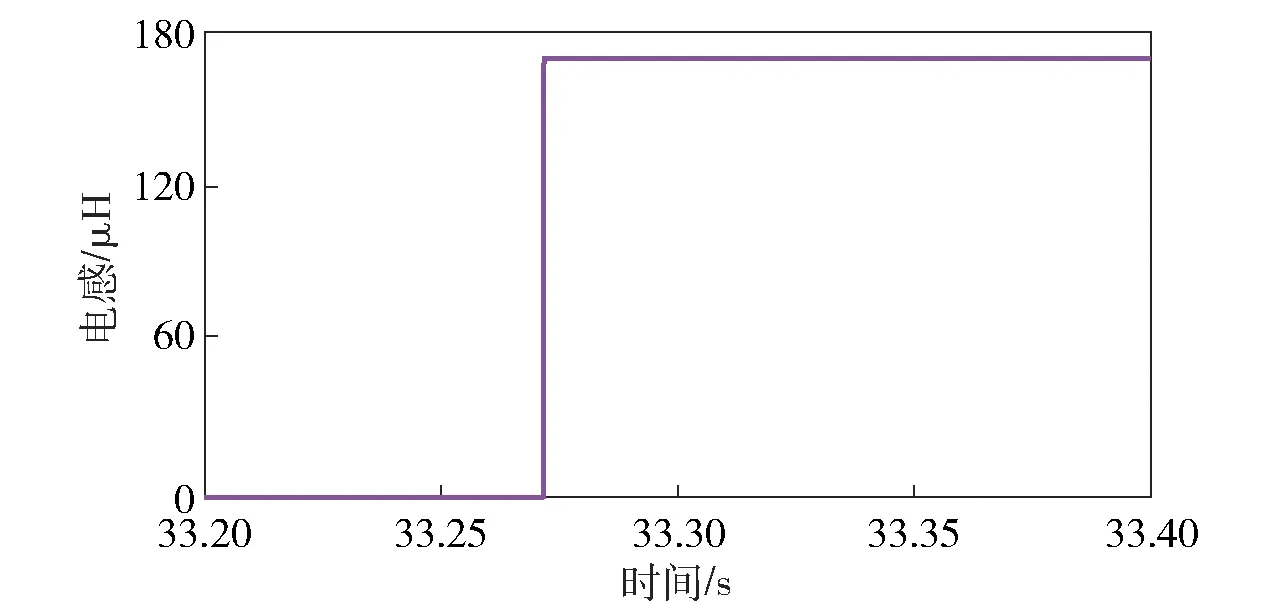
图16 20 kW永磁同步电机实验平台上直轴电感辨识结果Fig.16 Identified results of direct-axis inductance on 20 kW PMSM experimental platform

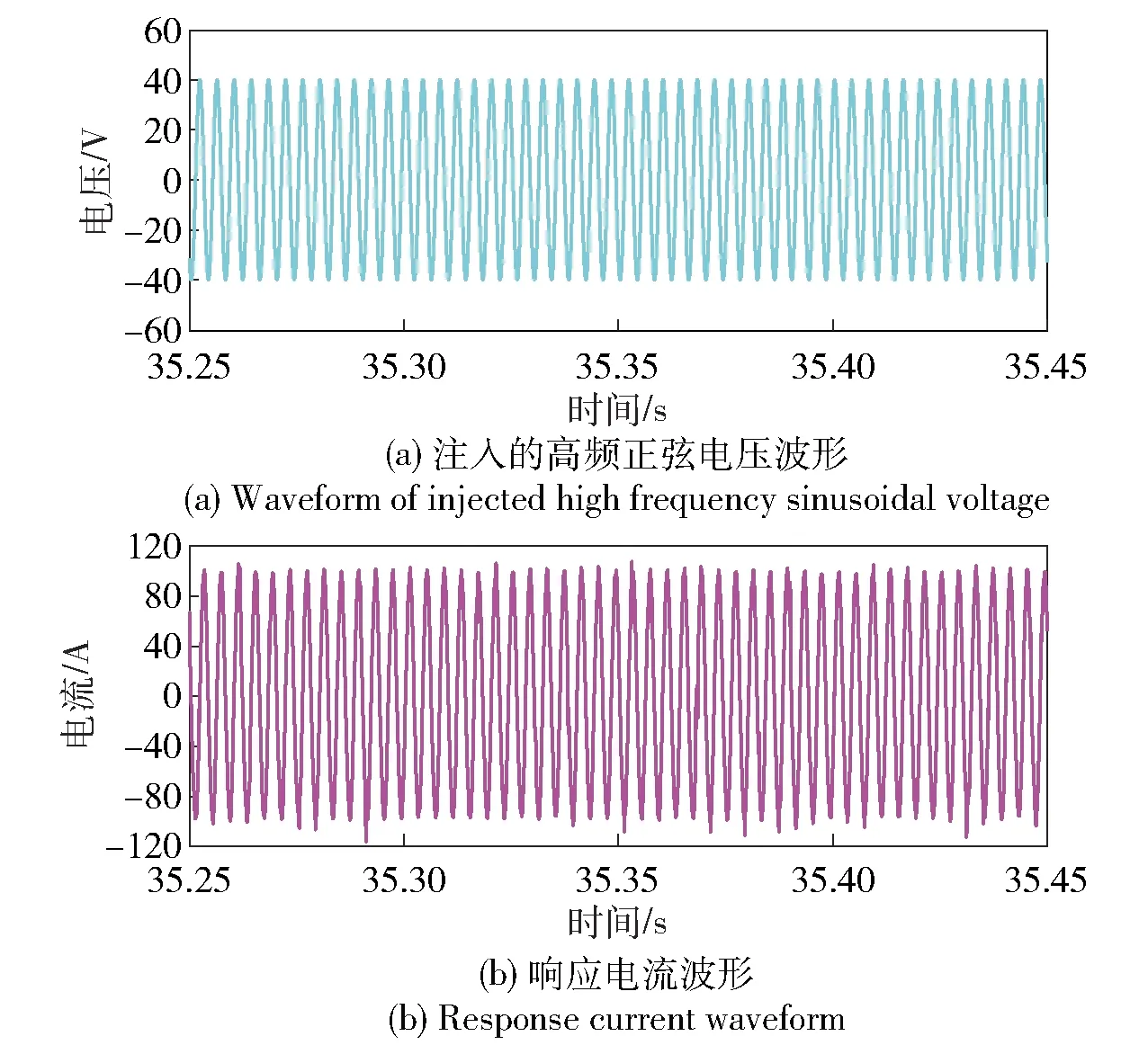
图17 20 kW永磁同步电机实验平台上辨识交轴电感时电压和电流波形Fig.17 Voltage and current waveforms for quadrature-axis inductance identification on 20 kW PMSM experimental platform

图18 20 kW永磁同步电机实验平台上交轴电感辨识结果Fig.18 Identified results of quadrature-axis inductance on 20 kW PMSM experimental platform

同样根据实验得到的电机参数进行电流环控制器参数的整定，电流环的期望截止频率设为200 Hz，得到控制器参数Kp=0.26，Ki=16.6. 如图19所示为20 kW永磁同步电机运行于400 r/min时，交轴电流指令从0 A升至20 A再升至40 A的电流响应波形，实验结果证明该方法同样可以使20 kW永磁同步电机具有较快的动态响应和良好的控制性能。

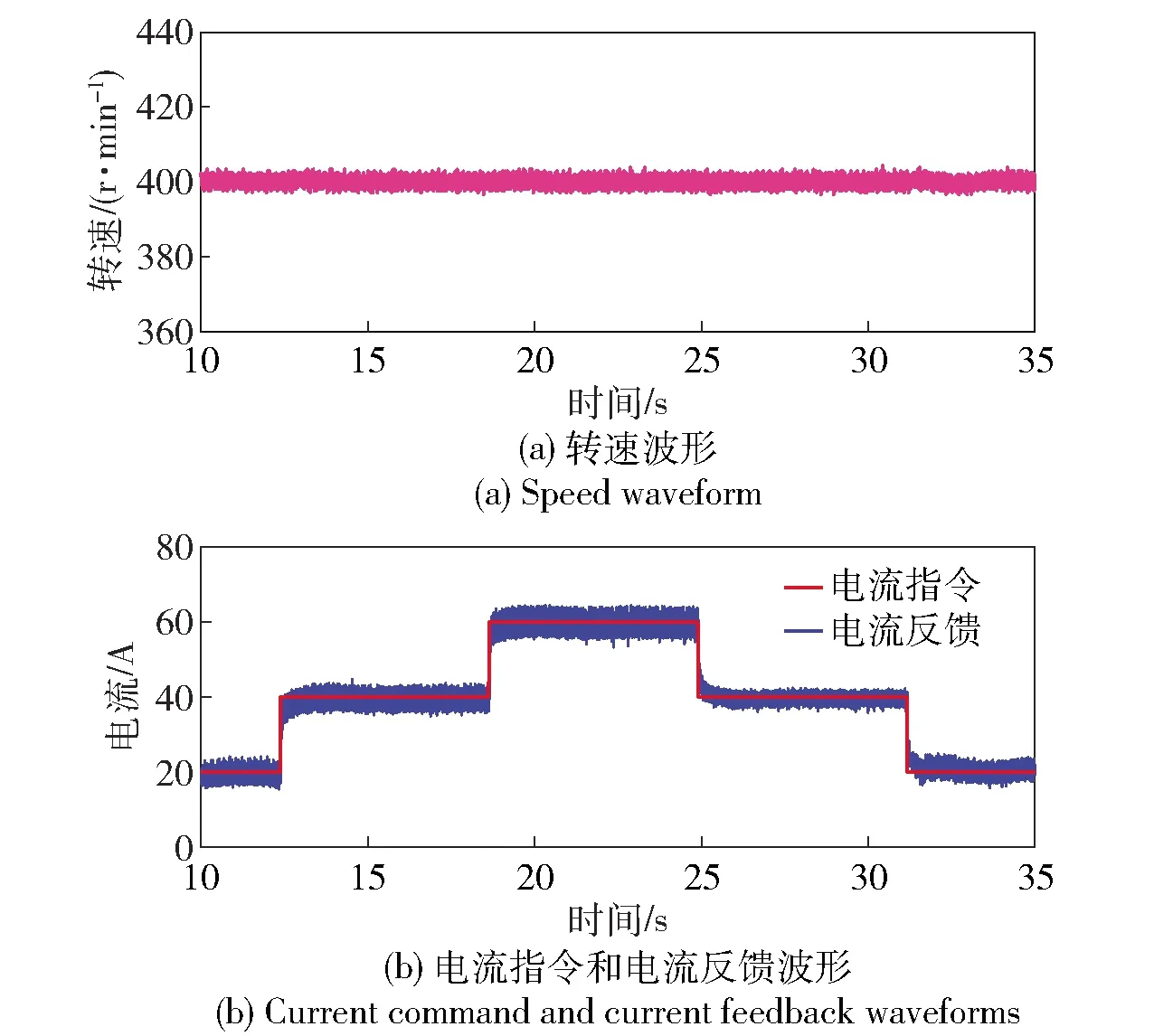
图19 20 kW永磁同步电机实验平台上交轴电流阶跃响应波形Fig.19 Quadrature-axis current step response waveform on 20 kW PMSM experimental platform

4 结论

本文结合电机静止参数辨识方法及电流环控制器参数自动整定方法，在电机静止条件下实现了对电机定子电阻及等效交直轴电感的辨识，并根据辨识得到的电机参数自动整定出可以直接用于电机控制的电流环控制器参数。得到主要结论如下：

1)本文方法逻辑清晰，实现过程较为简单，不需要额外的辅助工具。

2)采用本文方法可以实现当电机控制器应用于不同电机平台时都能够具有相对较好地控制效果，能更快更好地实现控制器的初始化。

3)实验分别在两个不同的实验平台上进行验证，实验结果证明了本文方法的有效性及通用性。