矿山法隧道复合式衬砌等效渗透系数计算及渗流分析

■马立铭

（三明莆炎高速公路有限责任公司，三明 365000）

复合式衬砌中排导系统对地下水渗流有着较大的影响，但复杂的排导系统在数值建模中往往难以精确地模拟，而通过将复杂的隧道防排水系统简化为具备相当渗透能力的透水衬砌可解决以上问题，所以衬砌等效渗透系数的求解则至关重要。 郑波等[1]通过引入虚拟的衬砌等效渗透系数k1*，将设置了防水板和排导系统的复合式衬砌的透水能力用等效渗透系数k1*表示， 并在此基础上利用整体式衬砌结构的水压力计算方法估算衬砌水压力，为复合式衬砌水压力的简化计算提供了有利条件。丁小平等[2]在前人研究的基础上，假定二次衬砌均匀渗水，并从隧道涌水量不变的角度出发，通过反演分析的方法得到复合式衬砌等效渗透系数的量化修正值k1*。 关振长等[3]提出基于防水密封垫失效的拼缝有效开度假定，进而推导出基于拼缝有效开度的盾构隧道渗流量及衬砌等效渗透系数的实用计算公式。 梁春雨等[4]通过理论与数值相结合的方法，研究了排水孔的参数对衬砌等效渗透系数的影响，为隧洞外水压的计算提供了参考。 另外，还有部分学者在应用轴对称解对隧道外水压力的计算[5-6]及隧道涌水量的预测[7]方面开展了一系列研究。

以上学者在对衬砌等效渗透系数进行解析求解的时候没有考虑初期支护的影响，对高压富水区的堵水限排复合式衬砌隧道而言，主要通过注浆圈和初期支护堵水[8]，故初期支护在衬砌等效渗透系数的求解过程中不容忽视。 依托莆炎高速公路三明境内的文笔山2# 隧道工程， 先利用理论公式计算透水二衬的等效渗透系数，并建立瞬态渗流模型分析隧道二次衬砌渗流流速的分布情况及涌水量的大小，最后通过比较实际隧道的渗流量与数值计算的渗流量大小，进一步验证理论公式的可靠性。

1 衬砌等效渗透系数

1.1 模型简化

以文笔山2# 隧道IV 级围岩复合式衬砌防排水系统断面为例（见图1），在应用退化的轴对称解计算隧道二次衬砌的等效渗透系数时，为保证隧道渗水面积不变，可利用“周长等效”原则将复合式衬砌隧道断面退化成圆形隧道断面进行求解（见图2），退化后的圆形隧道半径计算公式如下：

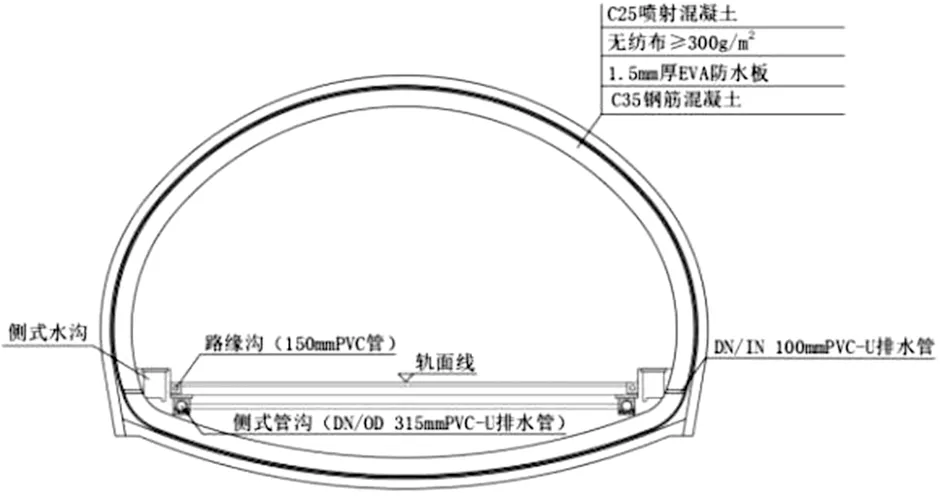
图1 IV 级围岩复合式衬砌防排水系统断面

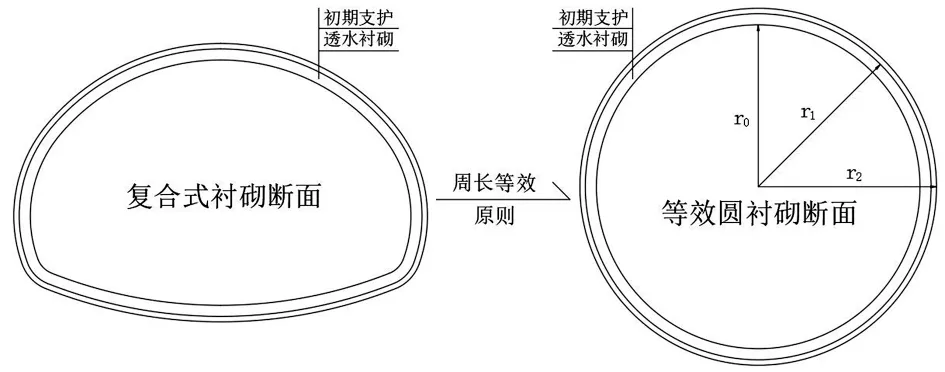
图2 复合式衬砌断面转换为圆形断面示意图

式中： r 为复合式衬砌等效半径； l 为复合式衬砌周长。

1.2 衬砌等效渗透系数

山岭隧道在施作初期支护、二次衬砌和注浆的情况下（见图3），利用退化轴对称解推导每延米隧道排水量的计算公式，推导过程如下：

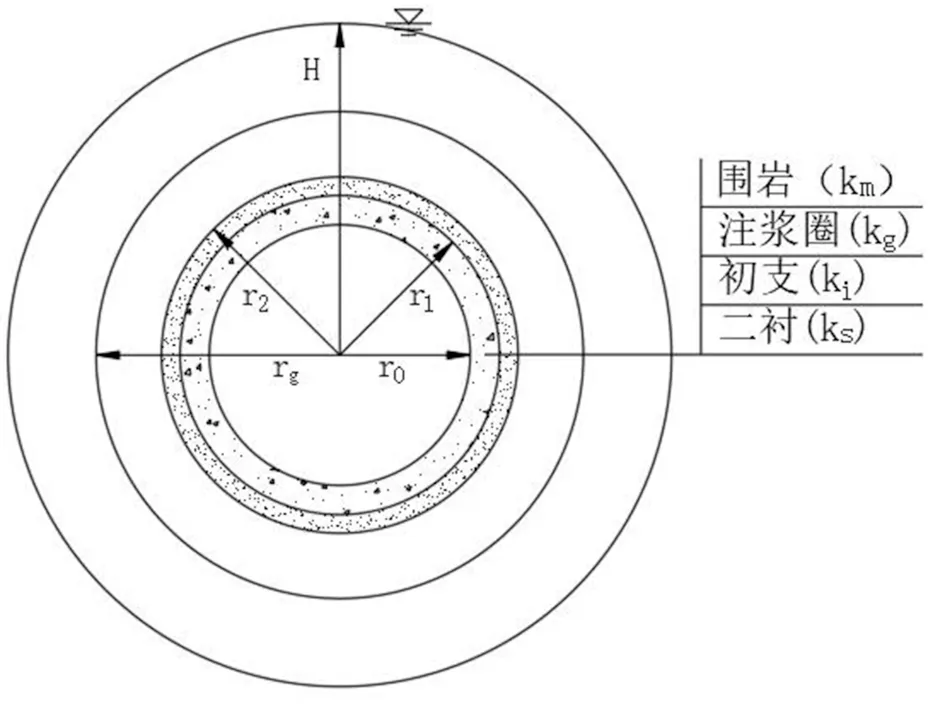
图3 轴对称圆形隧道简化图

式（2）～（9）中：Q3为二次衬砌施作后隧道的渗水量；h3s为二次衬砌范围内的水力势；h3i为初支范围内的水力势；h3g为注浆圈范围内的水力势；ks为二次衬砌的等效渗透系数；ki为初期支护的渗透系数；kg为注浆圈的渗透系数；km为围岩的渗透系数；r0为二次衬砌内半径；r1为二次衬砌外径；r2为初期支护外径；rg为注浆圈外径；H 为远场水力势， 即隧道中心位置处的地下水头。

2 工程实例

2.1 工程概况

文笔山2# 隧道进口位于东牙溪饮用水源保护区内，为双线分离式隧道，右隧起止里程为K223+375～K228+135，长4 760 m，属特长隧道，最大埋深670 m； 左隧起止里程为ZK223+394～ZK228+180，长4 786 m，属特长隧道，最大埋深660 m。

2.2 计算原型

从莆炎高速公路三明境 《工程地质详勘报告》中的隧道涌水量计算表（表1）可知：文笔山2# 隧道洞身在里程段K223+435～K223+730 范围内的围岩为中风化辉绿岩（岩脉），属于IV 级围岩，其渗透系数较大，隧道施工过程中的平常期涌水量、最大涌水量均为各个里程段中的最大值， 故选取K223+655.4 里程段的断面作为隧道计算原型。

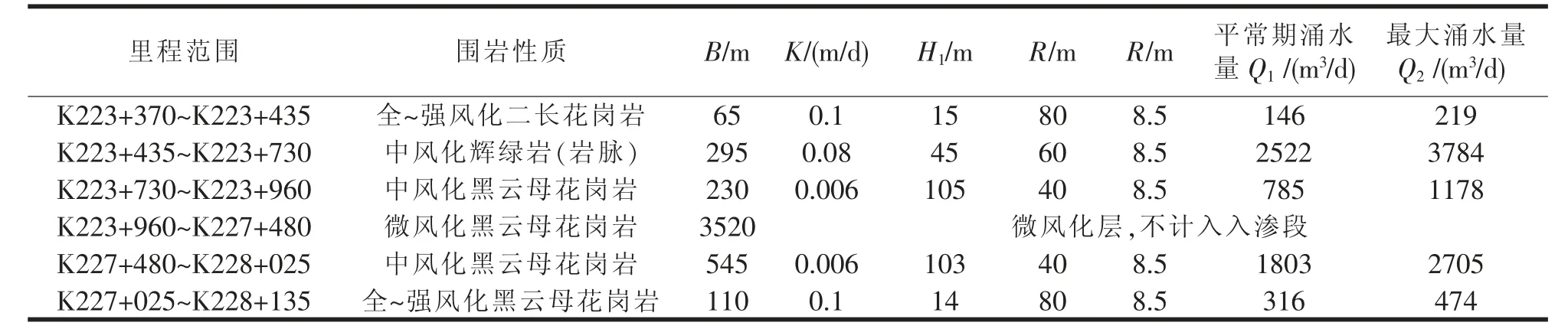
表1 隧道涌水量计算

2.3 计算参数

计算断面处的土层分布由上而下分别为：砂质粘性土、全风化辉绿岩、中风化辉绿岩，隧道洞身位于中风化辉绿岩层中， 地下水位位于地表以下67.5 m 处，具体的地质详情见图4。

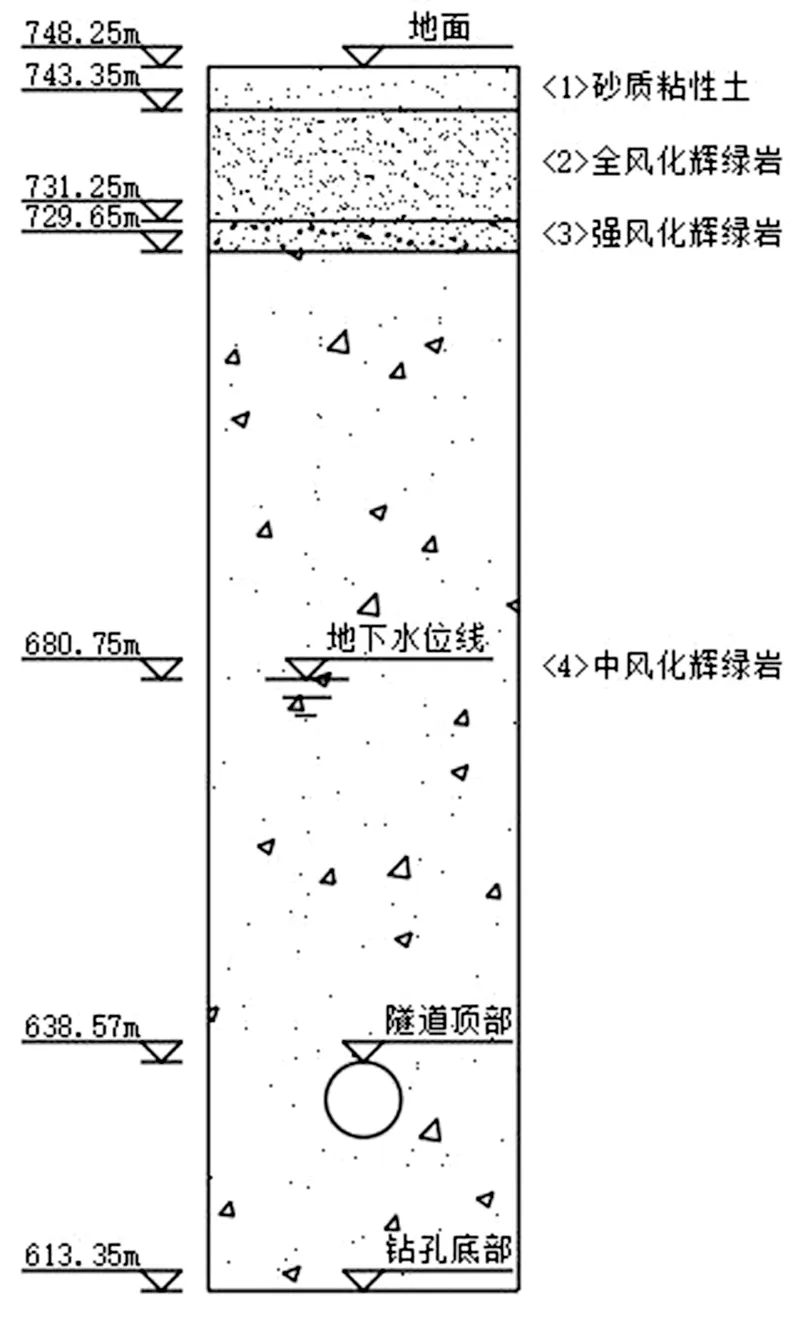
图4 计算断面钻孔柱状图

2.4 计算模型与边界条件

基于以上工程概况及相关参数，用ABAQUS 有限元软件建立平面应变模型。 从隧道开挖侧壁向两侧各取约8 倍洞径，模型横向共计300 m。数值模型顶部取地下水位线，隧道开挖面顶部至数值模型顶部的距离为42.18 m； 从隧道开挖面底向下取约10 倍洞高；模型竖向共计150 m。 其值大小具体的网格划分见图5。

图5 计算模型网格划分图

计算模型材料包括中风化辉绿岩、 注浆圈、初期支护及透水二砌，其中，中风化辉绿岩、注浆圈采用Mohr-Coulomb 本构模型，初期支护、二次衬砌采用弹性本构模型。

如图6 所示，模型的边界条件可分为力学边界条件、位移边界条件和渗流边界条件，具体如下：模型力学边界条件为：模型顶部施加与上覆土层相当的土压力，模型顶部的水压力为零，整个模型施加重力场。模型位移边界条件为：约束左右两侧。边界水平位移，约束底部边界竖向位移。 模型渗流边界条件为：隧道开挖后，毛洞边界为自由排水边界；施作初期支护后， 初期支护内边界为自由排水边界；施作二次衬砌后，二次衬砌内边界为自由排水边界。

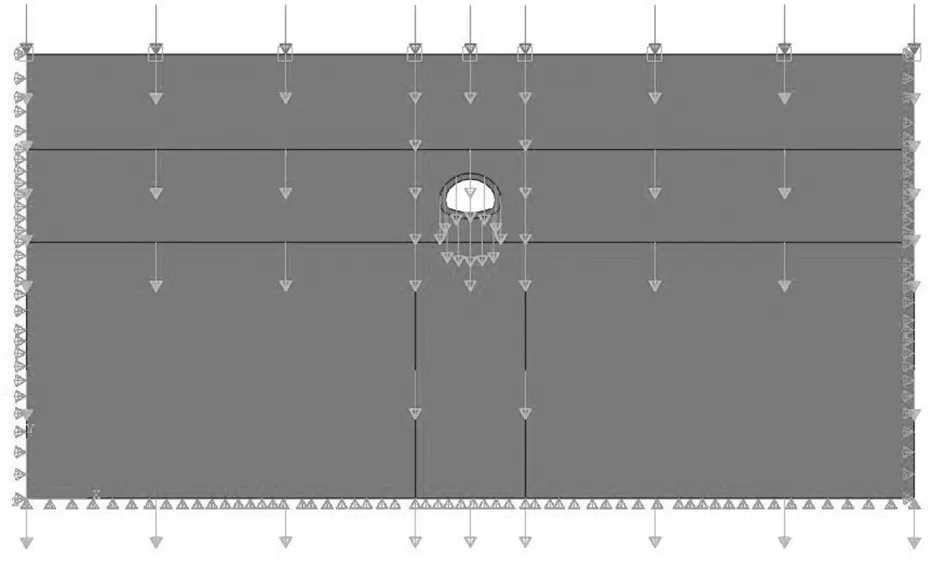
图6 边界条件图

2.5 计算结果

地下水渗流速度的变化能够较好地反映矿山法施工中隧道各个部位地下水的流动状况。 在隧道二次衬砌施作完成后， 地下水的渗流速度变化见图7， 可以发现隧道拱脚处的地下水渗流速度最大，其值vmax=0.3535 m/d。

图7 隧道流速矢量图

隧道渗流量的大小能够直接反映隧道施工造成的地下水资源流失状况。 透水二衬的节点流量云图及变化趋势图见图8， 从中可以发现隧道节点流量在拱顶A 处最小，其值RVFA=0.0381 m3/(m·d)；而后逐渐增大并在拱脚B 处达到峰值， 其值RVFB=0.0816 m3/(m·d); 最后又迅速降低， 在C 处其值RVFC=0.0416 m3/(m·d)。

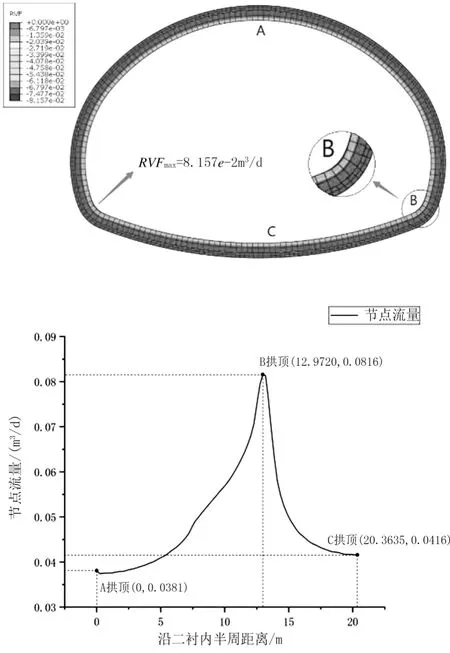
图8 透水二衬节点流量云图和变化趋势

由上述计算结果可知，拱脚处的地下水流速和节点渗流量是二衬内周中最大的，所以矿山法隧道复合式衬砌中的横向排水管宜设置在拱脚处，确保能够有效、迅速地排水，以降低二次衬砌背后的水压力。 另外，对二衬内周所有的节点流量进行求和得到渗流量Q=8.49 m3/(m·d)， 而实际隧道渗流量Q3=8.55 m3/(m·d)，两者相差0.7%，较为相近，故而可以验证1.2 节理论公式的可靠性。

3 结论

（1）对于设置了防水板和排导系统的复合式衬砌， 可以把排导系统和二次衬砌看作一个整体，即二次衬砌是透水的，从而应用退化的轴对称解对二次衬砌的等效渗透系数进行求解，起到简化数值分析过程的作用。

（2）在应用退化的轴对称解推导隧道二次衬砌的渗透系数时，为保证排水面积不变，可以利用“周长等效”原则将复合式衬砌断面简化为圆形隧道断面。 本研究在前人的理论基础上，进一步考虑复合式衬砌中初期支护的影响，并对隧道的渗流量和二次衬砌的等效渗透系数进行了理论推导。

（3）本研究基于文笔山2# 隧道的实际工程情况，结合二次衬砌等效渗透系数理论，建立了相应的隧道渗流耦合模型。 结果表明：数值模拟中隧道的渗流量Q=8.49 m3/(m·d)， 同计算的隧道渗流量Q3=8.55 m3/(m·d)相近，验证了理论公式的正确性。

（4）根据数值计算的结果显示：隧道的地下水流速大小和渗流量大小在拱脚处均达到了最大值，所以隧道的横向排水管宜设置在拱脚附近，从而达到迅速排水的目的，以降低二次衬砌背后的水压力大小。