地学统计学方法在辽河平原河谷渗透系数空间变化特性中的应用研究

赵振懿

(辽宁省营口水文局，辽宁 营口 115003)

平原河谷区由于地质地貌条件十分复杂，其渗透系数确定十分困难[1]。而对于平原河谷区而言，其地下水含量较为丰富，是区域水资源的重要组成部分[2]。平原河谷地区地下含水层渗透系数的准确确定对于分析其地下水资源量具有重要的意义。近些年来，平原河谷区的渗透系数研究取得一定的成果[3-6]，其中地学统计学方法[7-9]取得较好的成果。该方法结合变差函数的方法，在平原河谷地学分析的基础上，对平原河谷区的渗透系数进行时空变化分析。但是该方法还未在辽河平原河谷区得到应用。辽河平原河谷地下水较为丰富，近些年来，其渗透系数的确定一直是难点问题，为此本文结合地学统计方法，对辽河平原河谷的渗透系数空间变化特性进行分析，并对其渗透系数进行区划分析，研究成果对于辽河平原河谷区的渗透系数确定具有重要的参考价值。

1 研究方法

本文采用Box-Cox变换函数的方法来对样本数据的正态分布进行分析，其主要是对应变量y进行变换，其变换方程为：

(1)

式中，λ—变换参数。在提高样本正态分布后，结合变差函数理论来对区域的地学特征进行有效统计，变差函数的方程为：

(2)

式中，Z(x)—变量的二阶平稳变量观测值；h—相隔点距；Z(x+h)—相隔h下的观测值；E—数学期望值。对Z(x)进行实验变差，实验变差方程为：

(3)

式中，γ(h)—实验变差值；N(h)—统计样本数据对(Z(x)、Z(x+h))的对数。

2 研究结果

2.1 区域概况

本文以辽河平原区为研究实例，辽河平原为辽宁省最大的冲积平原，地貌类型十分丰富，从南向北，依次分布山前洪扇冲积平原以及山间斜坡冲积平原。地区降水从南向北逐步减少，区域地下水较为充沛，主要含水层为松散孔隙类的含水层组成结构，含水层质地主要为粗砂结构，含水层的厚度在6～18m左右。辽河平原的地下水系结构十分复杂，各含水层地下水相互补给，共同组成补给区以及排水区为一体的地下水循环系统。本文结合辽河平原区45处抽水站的实测数据，结合地学统计学方法，对辽河平原区的渗透系数时空变异性进行分析。

2.2 渗透系数统计特征值分析

结合区域抽水试验数据，对辽河平原区各含水层渗透系数的K值进行特征值的统计，统计分析结果见表1，并对其各含水层渗透系数直方图进行分析，分析结果如图1—2。

从表1中可看出，辽河平原区各含水层的渗透系数变化差异性较大，其含水层具有粗砂介质，也有类似黏土的细砂颗粒介质。承压含水层的渗透系数比潜层含水层渗透系数变化更为稳定。采用Box-Cox变换后渗透系数K值的离散差异减小，该方式可以有效降低样本数据的离散程度。从图1—2中可看出，初始K值渗透系数的直方图效果都较差，这主要是因为样本的离散程度较大，从直方图的变化可看出，正态概率下的K值稳定性较低。采用Box-Cox变换后其K值直方图都比其他2种方式有较为明显的改善，其中曲线性和正态概率分布情况均达到最优效果。

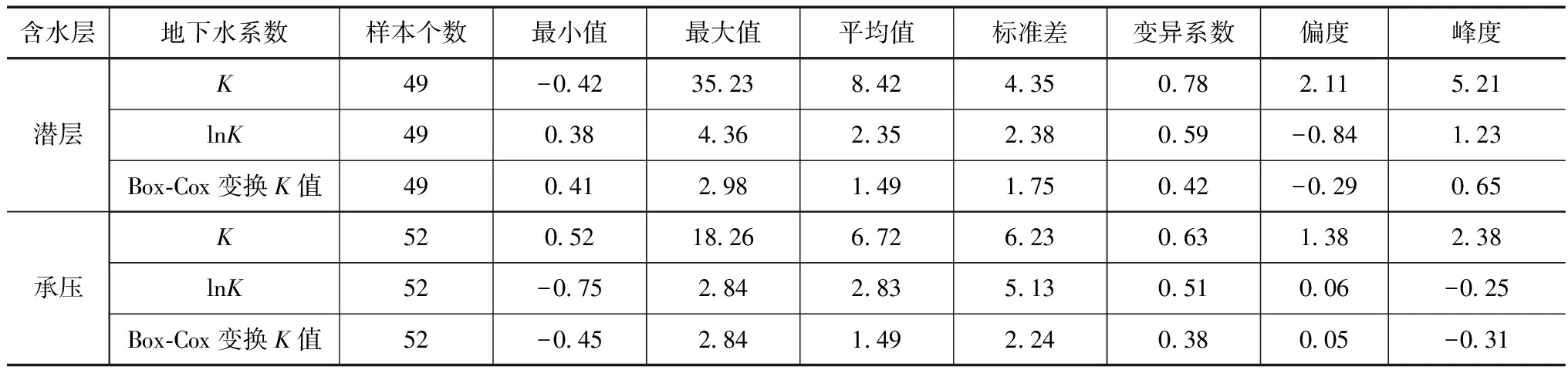
表1 各含水层渗透系数K值的统计结果

图1 潜水含水层渗透系数直方图

图2 承压含水层渗透系数直方图

2.3 渗透系数正态分布检验结果

采用2种方式对渗透系数各特征值参数的正态分布进行检验，检验结果见表2。

从统计检验结果可看出，采用Box-Cox变换后，其Sig值大于0.02，表明只有采用Box-Cox进行渗透系数样本数据的转换后，其样本数据才能在95%的置信水平下通过检验。通过渗透系数K值的变化统计分析可知，对于承压含水层而言，通过对数分布其承压含水层的渗透系数就可服从正态分布；而对于潜水含水层渗透系数而言，需要对其进行Box-Cox变化后才可服从正态分布，而对于承压含水层，采用对数变化后就可服从正态分布。

2.4 变差函数下渗透系数特征参数计算与拟合结果

通过上述分析后，采用变差含水方法对其渗透系数特征参数进行计算，并对其拟合结果进行分析，分析结果见表3。

从表3中可看出，通过变差函数对不同含水层的渗透系数进行转换后，其样本数据的平稳系列十分稳定，符合变差函数平稳随机系列的假设条件。从其拟合度上可看出，其指数拟合模型下的拟合程度最高，表明指数拟合模型在对各含水层渗透系数特征参数计算上具有一定的适用性。从其变程可看出，其空间滞后距离小于600m，表明在600m范围内其渗透系数的特征参数是具有空间相关性的。从2个函数层的基台值可看出，承压含水层的基台值较高，相比于潜水含水层，承压含水层的渗透系数K值的空间相关性更好。

2.5 渗透系数区划结果

对辽河平原区不同含水层的渗透系数进行区划分析，各含水层渗透系数区划分析结果如图3所示。

从各含水层渗透系数区划结可看出，辽河平原北部的渗透系数最低，潜水含水层渗透系数主要分布在0.5～8.9之间，而承压含水层的渗透系数主要分布在1.5～5.5之间。东南部渗透系数最大，承压含水层渗透系数总体从南向西逐渐减小变化。渗透系数空间变化，主要是受到区域水文地质的影响，北部区域水文地质主要为细砂颗粒，下渗量较少，而从北向南其主要从细砂向粗砂颗粒进行转变。此外各分区沉积物的厚度变化也是其渗透系数空间变化的主要原因之一，其区域沉积物的厚度越大，使得其南部的渗透系数明显高于其西部含水层的渗透系数。

表2 各含水层正态分布检验结果

表3 变差函数下渗透系数特征参数计算与拟合结果

3 研究结论

(1)辽河平原区河谷的各含水层渗透系数均表现出较为明显的空间相关性，其空间变异程度主要受到区域岩体结构的特性影响所致。

(2)对于潜水含水层渗透系数而言，需要对其进行Box-Cox变化后才可服从正态分布，而对于承压含水层，采用对数变化后就可服从正态分布。

(3)本文在进行渗透系数区划分析时，还未能探讨区域主要地貌类型对渗透系数的影响，在以后的研究中还应重点关注平原区河谷地貌类型变化对渗透系数空间变异度的影响。