路面寿命周期评价及养护决策探讨

■冯 雷

（河北交通投资集团公司，石家庄 050000）

目前我国公路行业正由建设期过渡到养护期，公路养护维修部门在面临养护决策时除了考虑降低总体维护成本外，还需要将路面状况对车辆燃油消耗和维护成本考虑在内，即路表较低的粗糙度水平会降低车辆燃油的消耗和车辆磨损，而且这对环境是有益的。 此外，为了保证道路运营通畅，路政部门往往需要进行更频繁的路面维护作业，以保持道路的服役性能，但在这一过程中通常会增加废气排放量且对环境产生不利影响。 但是，目前国内路面养护决策通常只考虑经济成本。

1 理论基础

Horvath 等[1]在选择路面类型（即水泥混凝土路面结构或沥青混凝土路面结构）时，认为必须要考虑可持续发展和环境的相关影响。Ekvall[2]认为LCA（全寿命周期评估） 技术是评估全寿命周期环境影响的基本技术。 迄今为止，许多研究人员[3-5]已将其应用于许多道路工程的建设中，其中包括高速公路等高等级路面。

由于交通荷载和老化引起的路面功能性退化，导致路面粗糙度（通常用国际平整度指数IRI 表示）增加，随后车辆运行速度降低，燃油消耗增加，最后导致二氧化碳排放量的增加。根据Yu 等[6]提出的模型，IRI 每增加1 m/km， 其相同状态下的平均速度就会降低0.84 km/h。 同样基于这一假设，提出了计算燃油消耗系数（FCF）的方法，以描述在老化路面上行驶车辆的实际燃油消耗[7]。 FCF 是一个取值大于1 的因子，提出了两个单独的方程：一个用于客车（公式1），一个用于卡车（公式2）。

式中，FCF—燃油消耗系数；IRI——国际平整度指数（m·km-1）。

Zhang 等[8-9]也提出了FCF 的计算公式，该公式也给出了IRI 和FCF 之间的简单线性关系，如公式（3）所示。Reger 等[10]认为，温室气体（GHG）排放与粗糙度引起的额外燃料消耗有关，同时也单独考虑了客车和卡车二氧化碳排放量的差异性。 假设油耗的变化与粗糙度呈线性关系，即每增加一个粗糙度单位（1 m·km-1），汽车的油耗增加1.05%，卡车的油耗增加0.725%。

本试验目的是研究使用阶段和养护阶段二氧化碳排放量与路面劣化程度之间的关系，同时确定路面劣化程度与加铺层厚度之间的关系。

2 计算模型

由二氧化碳排放水平决定的全球变暖潜能值（GWP），可以对路面维护活动（即各种厚度的热拌沥青覆盖层）和使用阶段的二氧化碳排放量进行评估。

2.1 二氧化碳排放量计算模型

为了研究道路使用阶段与建设阶段对环境影响的程度，可以通过计算两个过程的累积二氧化碳排放量进行表征，如公式（4）所示。

wn——加铺层厚度（mm）。

该公式假设是道路服役阶段的GWP 与路面的当前状况成正比，通过国际粗糙度指数（IRI）表示，而养护处理的GWP 主要取决于加铺层的厚度。

从公式（4）可以看出，通过以下两个方法可以使GWP 达到最小化：（1）在更加平整的沥青路面上行驶；（2）延长两次养护维修工作之间的间隔时间。

其中，路面养护阶段的改进程度取决于沥青加铺层厚度wn和处理前的路面状况s2n。因此，其改进模型如公式（5）所示。

2.2 路面劣化模型

1994 年，Tsunokawa 等[11]在提出了路面劣化模型，并在后续的许多路面设计和养护决策程序中得到了应用，如公式（8）所示。 该模型表征了随着路面使用时间的增长， 道面状况的变化遵循锯齿形轨迹；并且运用该模型的前提假设为检测率仅取决于路面的当前状况，该假设以公式（6）进行表示。

路面劣化模型如公式（8）所示：

式中，si——路面状态；F[s(t)]——基于当前路面状况的检测率；s(t)——在t 时刻的路面状态；f1——路面劣化过程的劣化因子，且劣化因子与道路所处的环境气候和交通条件有关；tn——路面使用时间。

上述公式所表征的含义为： 在经过时间tn之后，道路从状态s1劣化到状态s2。

3 路面状况与二氧化碳排放量关系研究

3.1 路面使用阶段二氧化碳排放量计算模型

HDM-4 模型通常用于计算路面使用阶段的CO2排放量。 该模型包含中型汽车和重型卡车的二氧化碳排放量模型。 基于数据模拟可以看出，对于重型车，当IRI 低于4 m·km-1时，粗糙度和CO2排放量之间存在着密切的线性关系。 然而，当粗糙度大于4 m/km 和5 m/km 时，在中型车和重型车模型中粗糙度和CO2排放量之间开始呈现出非线性行为，见图1 和图2。

图1 重型车二氧化碳排放量随粗糙度的变化

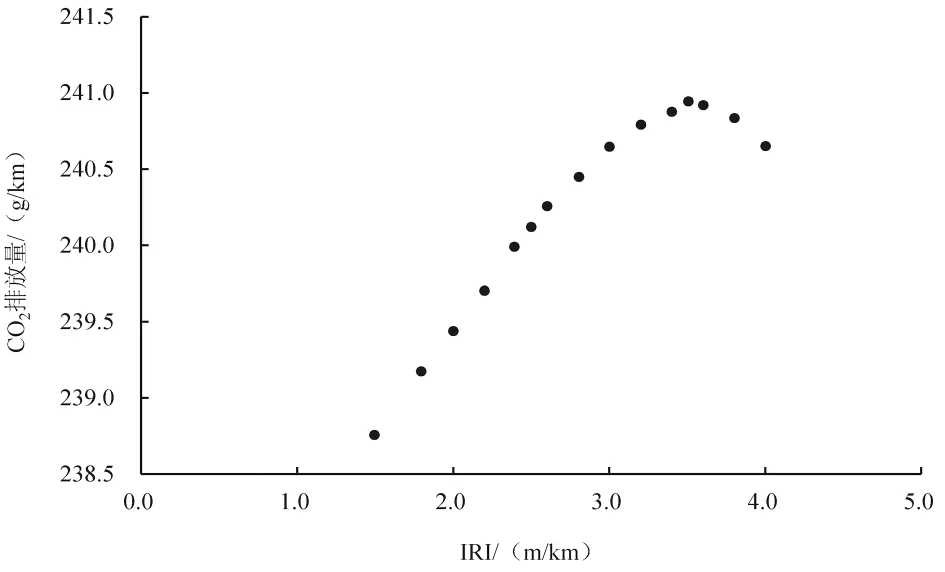
图2 中型车二氧化碳排放量随粗糙度的变化

表1 为中型车和重型车模型的回归参数。

表1 中型车和重型车拟合回归模型及回归参数

使用HDM-4 模型通过数据模拟获得的数据，可用于模型开发的线性和非线性回归。 中型车的线性模型回归系数R2等于0.869。 然而，二次多项式模型的回归系数R2等于0.986。 这说明非线性回归模型显示出比线性回归模型的结果更好。 因此，公式（9）给出了使用阶段二氧化碳排放量与路面状况（通过粗糙度指数）之间采用的关系。

3.2 路面养护维修阶段二氧化碳排放量计算模型

养护维修阶段实际上包括3 个独立的阶段，而在本研究中养护维修仅指在旧路面上加铺沥青罩面层，即不考虑生命周期的其他2 个阶段。 计算养护维修阶段二氧化碳排放量所采用的数据包括沥青混合料的体积组成（沥青与骨料的比例）、运输距离，以及用于运输和摊铺沥青混合料的设备等。 使用PaLATE 软件计算了二氧化碳排放量与加铺层厚度之间的关系，见图3。

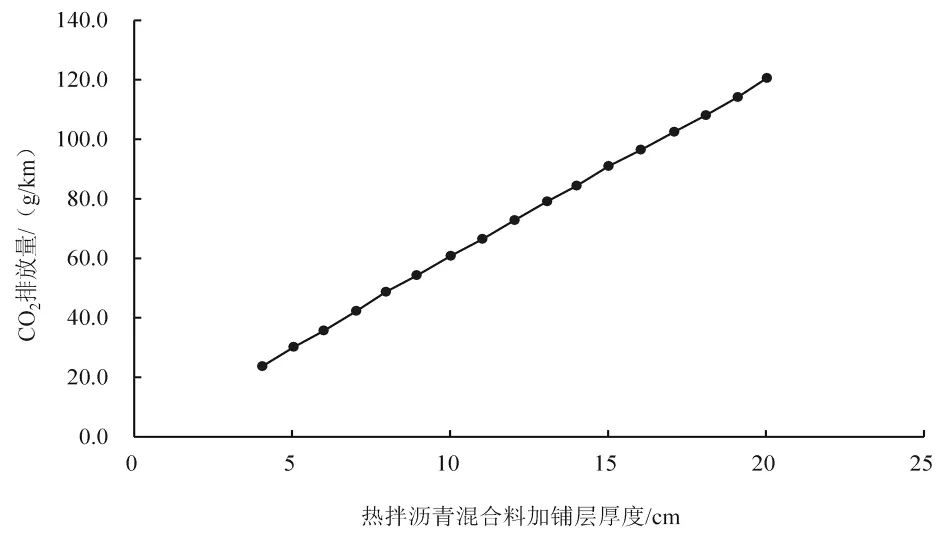
图3 养护维修阶段的二氧化碳排放量

从图中可以看出加铺层厚度与二氧化碳排放量之间呈现线性相关关系。 本研究建立了二者之间的线性回归方程，如公式（11）所示，其回归数R2为0.999。

4 路面劣化程度与加铺层厚度关系研究

为了进一步分析，本研究选取5 个现有的正常运营路段作为优化模型进行分析。 选取的5 个路段均为城市道路，路段1 为交通量相对较小的城市辅路，路段5 为交通量最大的主干道，而路段2～4 为交通量介于二者之间的城市交通联通道路。 优化模型以遗传算法为基础，利用上述模型，仅考虑IRI 值与二氧化碳排放量之间的关系。 该算法给出了一个最优解，即在先前定义的某个时间段内，使二氧化碳排放总量最小化。 另外，在计算前还需定义4 个约束条件：（1）分析期为30 年；（2）两个加铺层之间施工间隔的最短时间为4 年；（3）两个加铺层之间施工间隔的最长时间为12 年；（4）养护维修后路面的IRI 不大于2.0 m/km。

根据公式（8）可得试验结果如图4 所示，即根据路段的交通等级其路面养护维修的阈值也不相同。

图4 30 年分析期内5 个断面的国际粗糙度指数变化情况

在交通量较低的第1 路段中的分析期内，IRI的最大值为6.35 m·km-1，最佳的养护修复方案是采用厚度为7.0～8.0 cm 的加铺层。 然而，在交通量相对较高的第5 路段中的分析期内，需要对路面进行更多的定期养护；其IRI 的最大值是4.25 m/km，最佳养护方案是采用厚度为4.5～5.5 cm 的加铺层。

对于交通量适中的第3 路段，IRI 的最大值为4.33 m/km，最佳养护方案为铺设厚度为4.5～6.0 cm的加铺层。 其他2 个路段，即第2 路段和第4 路段，显示出类似的关系。

综上所述，在交通量较大的情况下，使用阶段产生的二氧化碳排放量远多于维护阶段二氧化碳的排放量。 因此，为了降低总体排放量，需要对其进行更为频繁的养护维修。

5 结论

（1）本试验研究了路面劣化程度与二氧化碳排放量之间的关系，对于路面使用阶段而言，重型车对路面平整度IRI 更为敏感，其二氧化碳排放量随IRI 值的增加呈线性增长。 中型车则对路面不平整度IRI 的敏感程度较低， 其二氧化碳排放量随IRI值的增加呈先增加后降低的一元二次多项式关系。

（2）在路面维修阶段，二氧化碳排放量与加铺层厚度呈线性关系。

（3）5 个实际路段的数值计算例子表明，沥青加铺层的厚度与IRI 之间有着密切的关系。 IRI 的最大值为4.25 m/km 时，加铺层厚度为4.5～5.5 cm，而IRI 的最大值为6.35 m/km 时， 加铺层厚度为7.0～8.0 cm；这说明为了使路面恢复合理的平整度，旧路面的IRI 值越高，其加铺层的厚度也相对较高。