悬灌法施工条件下超高墩连续梁稳定性分析

■田国伟

（永升建设集团有限公司，克拉玛依 834000）

1 引言

近年来， 随着国内外桥梁施工技术的不断完善，悬灌梁施工技术已逐渐完善，但在一些复杂恶劣施工工况下，该种施工方法仍存在一定的风险和挑战。 学者们就此进行了相应的探讨：鲁伟等[1]以某复杂山区悬灌梁施工为研究对象，对恶劣条件下悬灌梁的施工工艺进行了详细的介绍，研究结果可为类似工程施工提供一些参考；冯丽[2]对现浇预应力大跨度连续箱梁悬臂法施工中采用钢管混凝土柱临时支墩施工的设施设计进行了探讨；胡志华[3]以某连续梁临时支墩设计为研究对象，重点分析采用了钢管混凝土柱支撑时的稳定性，并依据数值分析方法对结构稳定性进行了验证分析；张茜[4]对悬灌法施工的连续梁、连续刚构0# 块托架的稳定性、安全性进行了优化设计；李林革[5]以某高墩大跨连续钢构桥为研究对象， 用有限元软件作为分析工具，重点分析了其在地震作用下的震动和破坏规律；丛义营[6]对高墩连续刚构桥悬灌段冬季施工技术进行了保暖措施的优化；丁凤臣[7]以某地区高墩连续刚构桥梁施工为分析对象， 通过对抽芯模板施工、空心墩垂直施工等关键施工技术的分析，并结合现场监测数据，给出了高墩连续刚构桥梁施工工程中的一些方法和建议。 综上所述，学者们对不同天气条件、施工环境下的悬灌梁的施工工艺都进行了一定的优化设计，本文在此基础上，以某地区超高墩悬灌法施工为研究对象， 通过采用大型有限元软件，重点分析了不同工况下结构的稳定性，并对相关影响参数进行了分析，研究结果可为类似工程设计和施工提供参考和借鉴。

2 工程概况

某大桥采用（64+122×2+64）结构布置形式，梁体为箱梁，长度为368.6 m，梁高在4.6 m～8.8 m，箱梁的顶板和底板宽度分别为8.4 m 和6.0 m。 桥墩高度最短的为96 m，最高的为114 m。 箱梁和桥墩分别采用C55 和C35 的混凝土，本文主要以高度为114 m 超高墩为研究对象，重点分析在最大悬臂状态时（此时的悬臂长度为60 m）和合拢状态下结构的稳定性，并分析相关参数改变带来的影响。

3 数值建模

3.1 模型建立

如图1 所示， 采用MIDAS 软件建立有限元模型，箱梁的顶板、底板宽度分别为8.4 m 和6.0 m，桥墩高度为114 m，最大悬臂长度为58 m，整个“T”型结构共划分为159 个节点和156 个单元，其中桥墩和箱梁分别为82 个和78 个。桥梁跨度为122 m，两端各取掉1 m，最终桥墩中心距离悬臂端为60 m（图1）。 箱梁和桥墩分别采用C55 和C35 的混凝土，箱梁、墩身和钢绞线的相关物理力学参数如表1所示。

图1 超高墩数值模型图

表1 超高墩结构物的物理力学参数

3.2 工况设置

如表2 所示， 本文共设置3 个不同计算工况，其中工程中采用的挂篮自重约780 kN， 外侧模、底膜、 箱梁内膜以及底膜防护的自重分别为55 kN、130 kN、60 kN、56 kN。 风荷载根据规范《公路桥梁抗风设计规范（JTG/T D60-01-2004）》进行计算，文中温差取10℃。

表2 工况设置

4 不同工况下结构稳定性分析

本文首先针对工况一， 对结构进行了一阶、二阶、三阶和四阶模态计算，经过计算可知，一阶、二阶、 三阶和四阶下的临界荷载系数分别为14.7、55.6、97.4 和146.2，对应的屈曲方向依次为纵向、横向、纵向和横向。 由此可知，工况一下一阶和二阶模态是控制结构稳定性的主要模态，且结构纵向稳定性和横向稳定性分别由一阶模态和二阶模态控制，由于一阶模态远小于二阶模态，因此，在工况一作用下，该结构主要失稳类型是纵向稳定性。 图2 给出了工况一时横、顺桥向的屈曲模态，规范规定纵向和横向临界荷载系数均为4.0，因此，该结构在工况一作用下均满足规范要求，处于稳定状态。

图2 工况一时屈曲模态

位移是反映结构、稳定最为直观和重要的数据，工况一时各关键点各方向位移如图3 所示， 可知悬臂端位移最大，其次是梁顶，最小的在桥墩1/3 处，表明结构越往上稳定性越差， 越接近桥墩底部稳定性越好，这与工况一所考虑的悬臂挂篮密切相关。

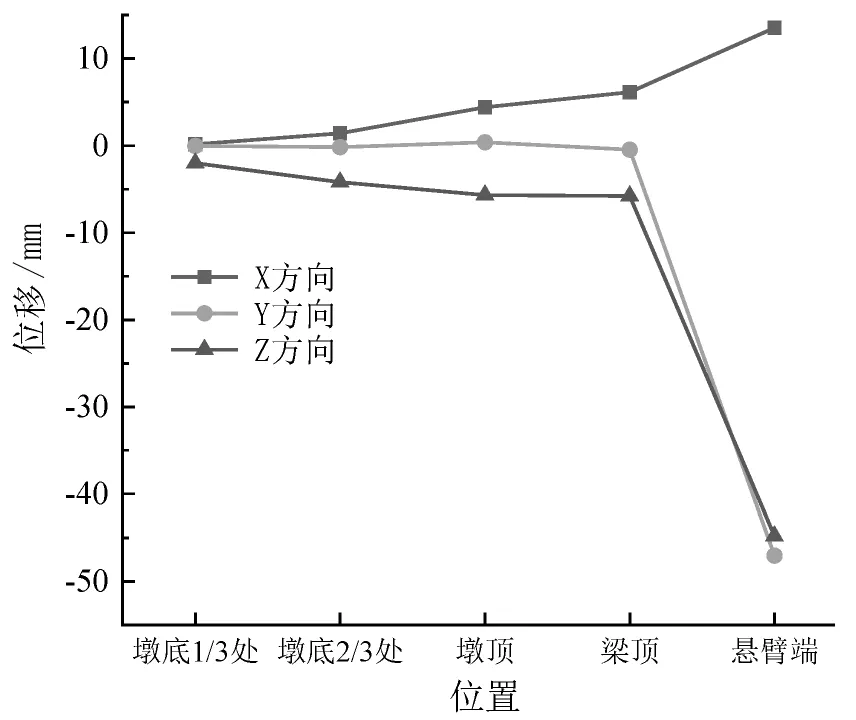
图3 工况一时各关键点各方向位移

由于一阶和二阶模态是控制结构稳定性的主要模态，针对工况二，对结构进行了一阶和二阶模态计算，经过计算可知，一阶和二阶下的临界荷载系数分别为13.8 和53.4，对应的屈曲方向依次为纵向和横向。由此可知，工况二下结构纵向稳定性和横向稳定性分别由一阶模态和二阶模态控制， 且由于一阶模态远小于二阶模态，因此，在工况二作用下，该结构主要失稳类型同样是是纵向稳定性。 图4 给出了工况二时横、顺桥向的屈曲模态，由于规范规定纵向和横向临界荷载系数均4.0，因此该结构在工况二作用下也均满足规范要求，处于稳定状态。

图4 工况二时屈曲模态

如图5 所示，给出了工况二时各关键点各方向位移，由图可知，在x、y 和z 方向，最大位移出现位置分别在梁顶、 梁顶和悬臂端， 最大位移依次为22.6 mm、100.4 mm 和55.9 mm。 工况二作用下的荷载形式为纵向风荷载， 在y 和z 平面内出现最大位移，且与工况一对比可知，y 方向位移增大将近20 倍，这表明纵向荷载会对结构的横向稳定性产生不利影响。

图5 工况二时各关键点各方向位移

针对工况三，对结构进行了一阶和二阶模态计算，经过计算可知，一阶和二阶下的临界荷载系数分别为14.5 和52.3，对应的屈曲方向依次为纵向和横向。 由此可知，工况三下结构纵向稳定性和横向稳定性分别由一阶模态和二阶模态控制，且由于一阶模态远小于二阶模态，因此，在工况三作用下，该结构主要失稳类型同样是是纵向稳定性。 对比工况一和工况二可知， 纵向临界荷载最大的工况一，最小的是工况二，即三种工况下，工况二时的结构纵向稳定性最差；横向临界荷载最大的工况一，最小的是工况三，即三种工况下，工况三时的结构横向稳定性最差。 综上可知，纵向风荷载同时对结构横向和纵向稳定性均有较大的影响，也说明了结构的稳定性主要由结构的纵向稳定性控制。 图6 给出了工况三时横、顺桥向的屈曲模态，由于规范规定纵向和横向临界荷载系数均为4.0， 因此该结构在工况三作用下也均满足规范要求，处于稳定状态。

图6 工况二时屈曲模态

如图7 所示，给出了工况三时各关键点各方向位移，由图可知，在x、y 和z 方向，最大位移出现位置均在悬臂端，最大位移依次为11.9 mm、201.8 mm和23.4 mm。 工况三作用下的荷载形式为横向风荷载，在y 和z 平面内出现最大位移，这表明横向荷载同样会会对结构的纵向向稳定性产生不利影响。

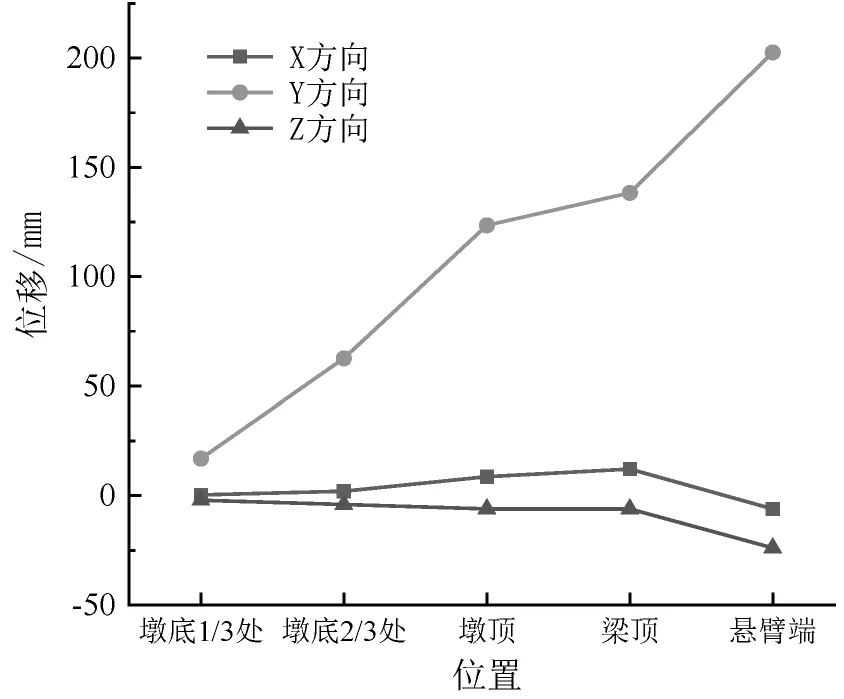
图7 工况三时各关键点各方向位移情况

5 结论

本文主要以某地区超高墩悬灌法施工为研究对象，通过采用大型有限元软件，重点分析了不同工况下结构的稳定性，并对相关参数的影响进行了分析，得到以下结论：（1）通过对结构的一阶、二阶、三阶和四阶模态进行计算，可知，各工况下一阶和二阶模态是控制结构稳定性的主要模态， 且结构纵向稳定性和横向稳定性分别由一阶模态和二阶模态控制，且由于一阶模态远小于二阶模态，结构主要失稳类型是纵向稳定性。 （2）根据各关键点位移曲线可知，结构越往上稳定性越差，越接近桥墩底部稳定性越好，三种工况下，工况二时的结构纵向稳定性最差，工况三时的结构横向稳定性最差。（3） 纵向风荷载同时对结构横向和纵向稳定性均有较大的影响， 也说明了结构的稳定性主要由结构的纵向稳定性控制。 （4）各工况下结构的纵向和横向临界荷载系数均大于4.0， 即结构三种工况作用下均满足规范要求，处于稳定状态。