基于虚拟同步发电机的惯量和阻尼自适应控制

孙宇新，王鹏，施凯，徐培凤

（江苏大学电气信息工程学院，江苏 镇江 212013）

伴随着工业革命的大浪潮，传统能源短缺问题成为我们急需面对的大挑战，与此同时，清洁无污染的可再生能源成为很好的替代品，于是以微电网为主的分布式电源的应用也越来越广泛[1-2]。传统的电力系统通常采用同步发电机作为主要电源，可以利用其转子的惯性，通过释放转子动能来维持系统稳定。由于大部分分布式电源不能直接并入电网使用，一般都需要用并网逆变器作为接口，但是传统的并网逆变器过载能力比较差，输出阻抗和惯性也都比较小[3-4]。为此，国内外学者提出采用VSG技术，通过改进控制方法模拟同步发电机（SG）的外特性，为电网提供惯性和阻尼，从而提高了逆变器抑制自身频率输出和功率波动的能力，增强系统的稳定性。

文献[5]提出了一种自适应旋转惯量的控制方法，通过在新的惯量控制环节加入低通滤波单元，抑制系统负荷变化造成的频率迅速波动，但是并未说明低通滤波单元的参数选取原则，且没有分析VSG并网功率发生扰动时系统的稳定性。文献[6]通过在功率侧加入由功率变化量和变化率的结合得到的辅助功率，从而实现强化惯量的控制，从结果可以看到系统的频率偏差明显得到改善，但是频率的变化率并未发生变化，且功率的偏差幅值变大。文献[7-8]都提出了一种自适应惯量的控制方式，分别构造了角速度变化率与虚拟惯性的关系，但是在拐点处角速度的变化率非常大，可能造成系统失稳，且忽略了阻尼的自适应作用。文献[9]提出了一种惯量阻尼自适应的控制策略，实现了惯量和阻尼的自适应交错控制，但是其控制策略设计的参数较多，且并未说明参数的确定原则。

针对以上问题，本文提出了一种自适应虚拟惯量和阻尼的协同控制策略，建立了虚拟转动惯量、阻尼系数与系统频率偏差量、频率变化率的关系，当系统发生功率扰动时，虚拟转动惯量和阻尼系数的大小会根据系统频率的偏差量和变化率而进行自适应地变化，从而有效减小了系统的超调，缩短了系统的暂态过程，提高了系统的稳定性。并通过仿真分析对控制系统中的自适应控制参数进行了确定。

1 VSG的基本原理

图1所示为VSG的结构模型与控制模型，其中结构模型中左侧的直流电压源代表微电网的电源，逆变控制系统等效替代同步发电机的作用。

图1 虚拟同步发电机结构Fig.1 Structure of VSG

通常情况下，为了方便分析，假设同步发电机的极对数为1，则同步发电机的机械角速度与电气角速度相等。根据传统SG的二阶模型，等效的转子运动方程如下式所示：

式中：J为同步发电机的转动惯量；D为阻尼转矩对应的同步发电机的阻尼系数；Tm，Te，TD分别为同步发电机的机械转矩、电磁转矩和阻尼转矩；θ等效为同步发电机的功角；ω，ωN分别为同步发电机的系统输出角速度和额定角速度，ωN等效为电网同步角速度；Pm，Pe分别为机械功率和电磁功率。

式（1）模拟了同步发电机的本体特性，VSG通过引入虚拟转动惯量J和阻尼系数D模拟SG的转子惯性和阻尼，这对于整个微网系统的频率稳定性具有非常大的改善作用。同时根据式（1）可以得到VSG的有功环，如图1中VSG的控制模型所示。

如图1中无功环所示，得到VSG控制的电压-无功控制环节如下式：

式中：Qm为参考无功功率；Qe为VSG输出无功功率；Dq为无功调节系数；K为积分系数；V为系统输出电压幅值；Vn为系统额定电压幅值；E为逆变器输出电压基波分量幅值。

2 自适应虚拟转动惯量和阻尼系数控制

2.1 转动惯量和阻尼系数对VSG的特性影响

本文研究的VSG控制均是在并网状态下进行的，因此忽略内环控制延时后，有功控制回路可以简化为如图2所示。其中，KP为简化的同步功率，大小为EU/Z，Z为VSG的虚拟阻抗、线路阻抗等其他零散阻抗之和。本文中为了便于分析，假设KP为固定的已知量。

图2 并网运行下的有功控制结构Fig.2 Structure of P control loop in grid-connected mode

由图2可以得到并网时有功控制回路的开环传递函数和闭环传递函数分别为

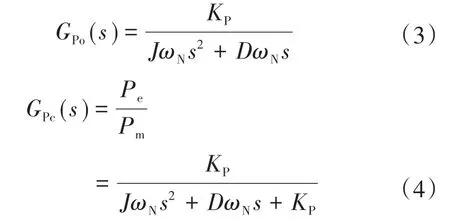
可以发现，有功回路对应的闭环传递函数为一个典型的二阶模型，则可以得到二阶模型对应的自然振荡角频率ωn和阻尼比ξ分别为

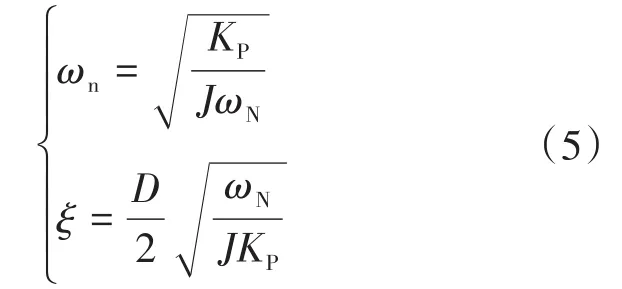
假设取0＜ξ＜1，误差带为±5%，则此二阶系统对应的最大超调量σ%和调节时间ts分别为

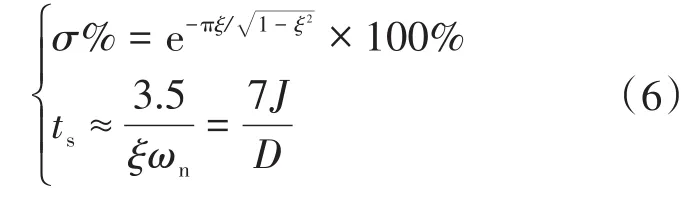
从式（6）可以得到，在有功功率以及无功功率都给定时，有功环对应的二阶模型的动态性能由转动惯量J和阻尼系数D来决定。其中惯量J主要对频率的变化率有较大的影响，阻尼D对频率的偏差量有较大的影响。

2.2 自适应控制原理

当VSG在并网条件下发生功率扰动时，功率与系统频率都会在扰动的瞬间出现衰减震荡，而震荡的超调量与趋于稳定的时间是评判系统稳定性的关键参数。如图3所示，当VSG的给定有功功率由P1突增为P2时，整个系统的稳定运行点也从A点切换到B点，在这个过程中，系统功率和频率变化均为衰减震荡。

图3 虚拟同步发电机的功角和角速度曲线Fig.3 Power angle curves and angular velocity curves of VSG

为便于进行分析，在转动惯量和阻尼均为固定值时，将衰减振荡的过程分为4个部分：①t1—t2；②t2—t3；③t3—t4；④t4—t5。如图 3 所示，在区间①内，发生扰动瞬间，频率会发生突增，即VSG的角速度大于电网的角速度，如图3d所示，且会持续增加，即角速度的变化率 dω/dt＞0，因此，此时应增大虚拟转动惯量J与阻尼系数D来抑制角速度的超调幅值以及角速度的变化率。此时Δω（dω/dt）＞0；在区间②内，转子角速度依然大于电网角速度，即Δω＞0，但是角速度处于减速阶段，转子角速度的变化率dω/dt＜0，因此应适当减小转动惯量，使角速度加速恢复到额定值；当转动惯量J不变时，阻尼D的增大同时会使dω/dt减小，因此应适当减小阻尼D，避免由于过大的阻尼D抵消转动惯量J的作用。此时Δω（dω/dt）＜0；区间③、区间④与区间①、区间②原理类似，不再详细分析。当系统恢复正常，功率从P2恢复到P1时，系统稳定点从B点切换到A点，其整个过程与上述分析一致，不再赘述。

根据分析结果可以得到表1所示的自适应虚拟惯量和阻尼系数的选取原则表。

表1 虚拟惯量和阻尼系数选取原则Tab.1 Selecting principle of J and D

由于ω=2πf，所以 Δω，dω/dt，Δω（dω/dt）的正负变化与 Δf，df/dt，Δf（df/dt）一致，因此根据表1所示的虚拟转动惯量与阻尼系数的选取原则，可以得到自适应控制策略为

式中：J0，D0分别为VSG稳定运行时的转动惯量和阻尼系数；KJ，KD分别为转动惯量和阻尼的调节系数；TJ，TD分别为频率的偏差速率阈值和频率偏差阈值。

根据表1和式（7）可以得到自适应控制原理图如图4所示。在区间①内惯量增大后值为J0+KJ|Δf（df/dt）|；阻尼系数增大为D0+KD|Δf（df/dt）|；在区间②内转动惯量应适当减小，恢复到恒定惯量J0即可，阻尼系数也适当减小，恢复到D0，使频率快速减小到稳定值；在区间③、区间④内，惯量和阻尼的变化情况与区间①、区间②类似。

图4 自适应控制原理图Fig.4 Adaptive control schematic

3 参数整定

一般情况下，VSG稳定运行时的转动惯量J0和阻尼系数D0都按照“最优二阶系统”的方法整定，使系统能够获得较快的响应速度和较小的超调量。

3.1 确定参数KJ和KD

根据第2节有功环传递函数式（3）、式（4）可以得到不同转动惯量J和阻尼系数D下有功环的根轨迹簇如图5所示。

图5 不同J和D下有功环的根轨迹Fig.5 Root locus with different J and D

从图5中可以看到，当J分别为0.01，0.05和0.08时，D从0增大到无限大的根轨迹。s1和s2是系统的一对共轭复根，按照图中箭头所示的方向运动，同时也是D从0缓慢增加的方向。可以发现，随着D的增大，s1和s2同时向复平面的左侧移动，说明此时系统的动态性能较好，系统处于欠阻尼状态，为衰减振荡，有一定的超调；但随着D的继续增大，s1和s2逐渐在实轴上会合，虚部变为0，此时对应的是系统的临界阻尼状态；如果D继续增大，s1和s2都将在实轴上沿相反方向运动，此时系统处于过阻尼状态，会造成系统的调节时间增加，因此阻尼系数D不能过大。另外一方面，从图中可以发现，随着J的增长，特征根s1和s2的分离点逐渐趋于0，即逐渐向虚轴移动，造成系统的响应速度变慢，因此转动惯量J也不能太大[10]。

文献[4]推导了惯量J和D之间的约束方程，并给出了J和D的选取范围。因此本文所提出的控制策略的自适应惯量和阻尼都应满足文献[4]中的参数选取范围，即可得Jmax，Dmax。

由式（7）可知惯量和阻尼调节系数范围为

代入数据可得KJ≤0.75，KD≤3.05，具体的调节参数大小通过仿真结果进行进一步的确定。

图6为系统发生功率扰动时的频率变化曲线。在对惯量和阻尼调节系数进行整定时，首先调节KD=0，分别选取KJ为0.25，0.50，0.75和1.00，系统发生功率扰动时的频率变化曲线如图6a所示。从图6a中可以发现，随着KJ的增大，频率的变化速度明显变缓，但是稳定时间却变长了，且当KJ=1.00，即超过确定范围时变化尤为明显；然后调节KJ=0，分别选取KD为1，2，3和4，系统发生功率扰动时频率变化曲线如图6b所示，从图6b中可以看到，频率的振荡幅值得到了明显的降低，但是当其调节参数超过确定范围时，震荡的周期变长了。因此分别根据其控制效果，按照取中的原则进行参数的确定。

图6 调节KJ及KD时系统频率变化曲线Fig.6 System frequency change curves when adjusting KJand KD

3.2 确定参数TJ，TD

VSG正常运行时，系统的频率会有较小的波动，但是频率的变化率并不能够忽略不计。TJ作为频率的偏差速率阀值，用来判断是否进行自适应惯量的切换开关，为避免正常运行时的误操作，TJ一定要大于VSG正常运行时频率偏差速率的最大值，同时为了提高自适应系统的精度，TJ也不能太大，因此只需要满足避免误操作即可。频率的偏差阈值TD同理可得。

4 仿真实验

为验证本文所提控制算法的正确性和有效性，本文在Matlab/Simulink仿真软件平台搭建了单台VSG并网的仿真模型。仿真系统的主要参数如下：直流侧电压Vin=800 V，电网电压Ug=220 V，额定频率fN=50 Hz，滤波电感L1=4 mH，网侧电感L2=0.8 mH，滤波电容C=10 μF，开关频率fK=10 kHz，J=0.07 kg·m2，D=4.62 N·m·s·rad-1，KD=2，KJ=0.5，TJ=2.5，TD=0.015。

本次仿真的模型为：VSG先进行预同步，在1.5 s左右进行并网后，分析有功功率发生扰动时系统的稳定性，仿真时长为3 s，其中2 s以前VSG给定输出有功功率都为10 kW，在2 s时有功功率突增为14 kW，在2.5 s又恢复为10 kW。

图7为不同控制策略下VSG的输出有功功率变化曲线。VSG在并网状态下，在2 s功率由10 kW突增为14 kW，此时功率会发生超调。传统惯量阻尼控制、自适应惯量控制与自适应惯量和阻尼协调控制的有功功率超调量分别为14.28%，10.86%和3.28%；再次恢复稳定所需时间分别为0.22 s，0.20 s和0.14 s。在第2.5 s功率恢复到10 kW时，同样可以看到自适应惯量和阻尼协调控制的有功功率振荡幅值和调节时间明显减小。因此可以得到结论：当功率发生扰动时，自适应惯量和阻尼控制可以有效抑制功率的振荡。

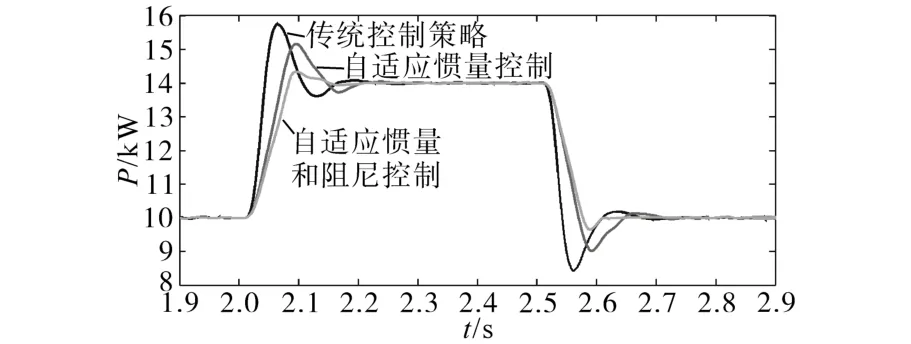
图7 虚拟同步发电机的有功功率变化曲线Fig.7 Active power curves of VSG

图8为不同控制策略下VSG输出频率的变化曲线对比。在第2 s功率发生突增后，传统惯量阻尼控制、自适应惯量控制与自适应惯量和阻尼控制的输出频率偏差分别为0.34 Hz，0.18 Hz和0.09 Hz。可以看到，自适应惯量控制能够有效地抑制频率的变换速度，减小超调范围，但在加入阻尼的自适应控制后，进一步减小了频率的偏差范围，并缩短了调节时间，完全满足国家的要求标准。

图8 虚拟同步发电机的频率震荡曲线Fig.8 Frequency oscillation curves of VSG

图9所示为VSG发生扰动后的虚拟转动惯量和阻尼系数变化大小，由于频率变化拐点处的df/dt变化较大，造成惯量和阻尼都在2.04 s左右有一个突刺，但都在系统稳定允许的范围内。

图9 VSG的惯量和阻尼变化曲线Fig.9 The variation curves of VSG parameters J and D

图10所示为VSG在不同控制策略下的输出电流波形对比，其中，图10b为图10a中虚线框部分的局部放大图。可以看到，当系统功率发生突变或者骤降时，传统控制的VSG输出电流也都会发生突增或者骤降，而本文提出的自适应控制策略能够有效地抑制电流的突增和骤降，使其平稳地过渡。

图10 不同控制时电流对比Fig.10 Comparation of current among different control modes

5 结论

针对分布式电源大量并网时由于功率扰动带来的稳定性问题，本文提出了一种新型的自适应虚拟惯量和阻尼控制策略，得到以下结论：

1）结合转动惯量和阻尼系数分别对系统稳定性的影响，并通过分析VSG的功角和角速度变化曲线，最终得到自适应惯量和阻尼的控制方案。

2）通过对仿真得到的波形图进行分析后可以得到结论：与传统的VSG控制方案相比，本文所提出的自适应控制策略不仅可以抑制频率的变化速度，还能够降低频率的偏差量。

3）本文只对单台VSG的功率扰动情况进行了研究，并未研究多台VSG并联时的情况，这也正是课题组接下来研究方向的重心。