寄生参数对高增益准Z源逆变器的性能影响

房成群，国珍，郝杨阳，李恺，李海滨，张民

（青岛理工大学信息与控制工程学院，山东 青岛 266520）

大功率电力电子装置在社会生产与日常生活中，从研究到实际工程应用，已取得较好的经济效益[1]。尤其在光伏并网中，高升压能力、高性能的变换器是必不可少的[2-4]，而Z源及其衍生拓扑因其引入直通状态大幅提高了变换器的电压增益与效率[5-7]。但是由于电路器件中不可避免的寄生参数，会对系统的可靠性造成无法忽略的影响[8]。

文献[9]提出了一种基于单相Z源逆变器的改进型PWM控制策略，并通过对开关管、二极管、电感的损耗计算进行了效率分析，但是其分析过程比较简单。文献[10]提出了一种新型准Z源拓扑，并对其进行了更为详细的损耗分析，但主要是对不同控制策略下的电路损耗对比。文献[11]提出了一种新型准Z源变拓扑结构并做了损耗分析，在前人的基础上非常细致地分析了IGBT与二极管的损耗，但对逆变器中的寄生参数影响考虑得不够全面。

传统的变压器型（准）Z源逆变器[12-13]的结构比较简单且具有高升压能力，但耦合电感的漏感在产生电压尖峰的同时会对逆变桥开关管造成冲击且影响逆变器的效率。一种高电压增益耦合电感准Z源逆变器（switched coupled-inductor quasi-Z-source inverter，SCIqZSI）切实解决了这类问题，其原理如图1所示，二极管D1的引入，使得耦合电感Np的漏感在电路非直通时产生的电压尖峰被电容C2钳位，降低了逆变桥上的开关管的电压应力，同时漏感能量得到重复利用，提升了逆变器的转换效率。开关管的低应力可以改善电路的可靠性，还可以选择廉价的低应力开关管，降低逆变器的成本[14-15]。

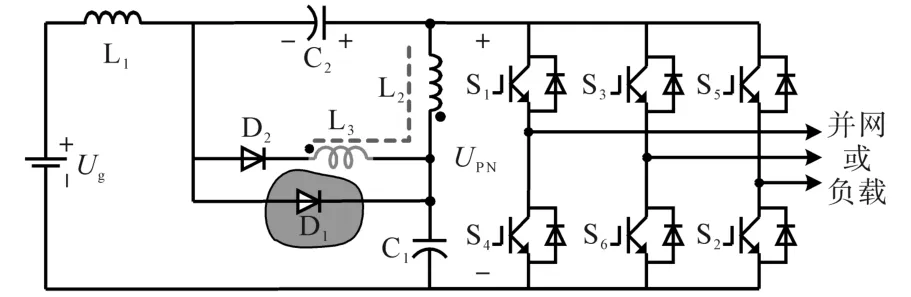
图1 高增益耦合电感软开关准Z源逆变器Fig.1 Switched coupled-inductor quasi-Z-source inverter with soft-switching condition

本文研究了SCIqZSI电路中寄生电阻及漏感对变换器的性能影响，通过研究寄生参数对变换器损耗和效率的定量分析，为改善SCIqZSI电路综合性能提供了理论依据。文章第1节研究了考虑寄生参数时电路的稳态运行情况，第2节详细量化了各寄生参数对变换器效率的影响，第3节根据前面理论推导对变换器性能进行了量化研究，第4节则是对变换器进行仿真并在实验室制作1 kW样机进行实验验证，最后得出了结论。

1 寄生参数条件下稳态分析

Z源逆变器有9个工作状态，分别是6个非零状态，2个零状态，1个直通零状态。为了便于分析，在文中，SCIqZSI的工作状态被简化为两种，分别是直通状态和非直通状态。输入电压为Ug，根据文献[5]可以得出变换器在理想状态下的电压增益B为

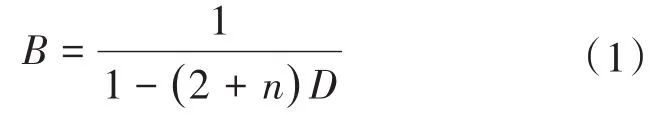
式中：n为耦合电感原边与副边匝数比；D为逆变器直通占空比。

SCIqZSI带有寄生电阻的工作过程图如图2所示。储能电感、耦合电感、电容以及开关管存在寄生电阻，各寄生电阻分别在图中标识为rL1，rLa，rLb，rC1，rC2，rs；Seq为三相逆变桥的等效开关。

图2 变换器在寄生电阻影响下的工作过程Fig.2 Working process of converter under the influence of parasitic resistance

有寄生电阻存在情况下，电路的电流分析与理想情况下相同，令输入电流为Iin，直通模式时，母线电压为0，流经逆变器的电流为ish，非直通模式时，直流母线电压为UPN，流向负载的电流为IPN，而理想状态输入输出功率相等，可得：

根据图2可知：

由电容安秒平衡定律可得：

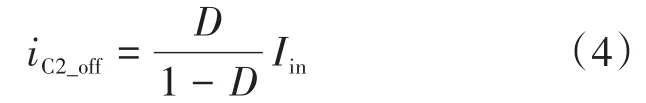
由图2b可以看出：

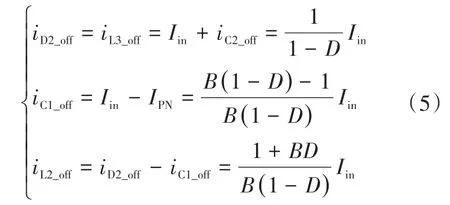
根据式（5）通过电容安秒平衡定律可得到电容C1直通时的电流：

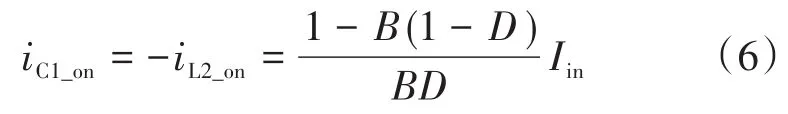
最后，可得：

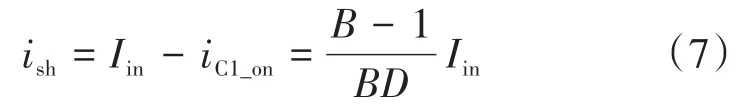
以上公式中“on”代表直通时流经相应器件的电流值，“off”代表非直通时流经相应器件的电流值。

从图2a可以看出，直通状态下的电路开关管处于导通状态，电路可等效为开关管将后级短路，此时电路内各路电压关系为

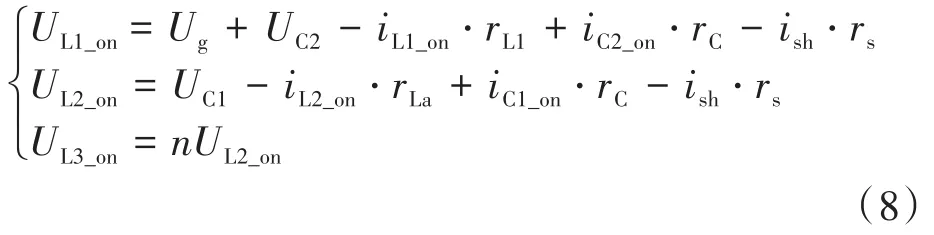
图2b为非直通工作状态下的等效电路，此时电路后级可用一个负载电阻来替代，则电路内电压关系为

式中：UL1_on，UL2_on，UL3_on，UL1_off，UL2_off，UL3_off，分别为直通、非直通状态下电感L1以及耦合电感L2，L3上的电压；UFD2为二极管D2导通压降。

此时，令有寄生参数存在情况下的电压增益为B*，理想情况下电压增益为B，电路输出电流为Io，输出端负载的等效电阻为R，且有寄生参数存在下电路电流关系不变，因此有：

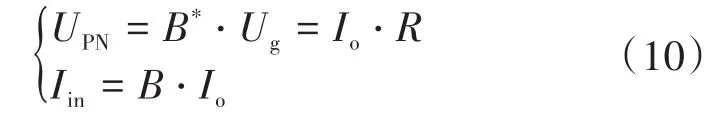
根据式（10）可得：

分别对电感 L1，L2，L3进行伏秒平衡计算，并将结果与式（2）～式（7）中各电流与输入电流关系和式（11）联立可得到：

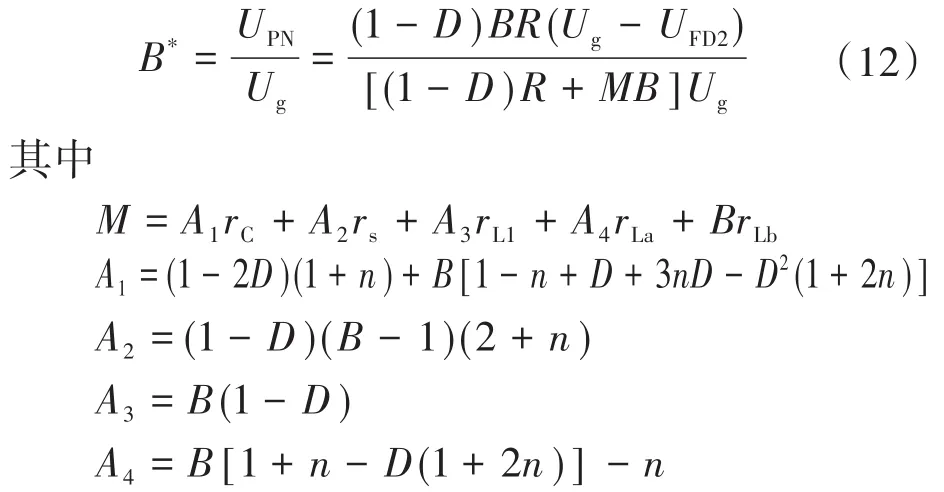
由于负载在逆变器直通工作状态下被短路，故非直通状态下的变换器输入、输出功率可以表示为

式中：Dsh为直通占空比；T为周期时间。

于是可以得到整个逆变器的效率为

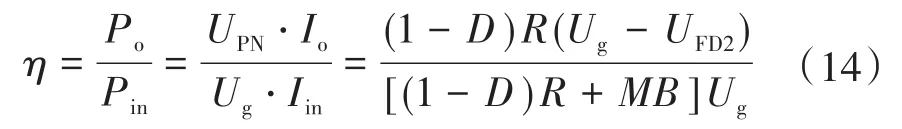
为了验证此变换器有寄生电阻影响下的电压增益的推导准确性，将式（12）中寄生电阻相关值忽略，可得到与理想状态下相同的电压增益，说明了公式推导的正确性。

2 寄生参数条件下效率分析

SCIqZSI带有寄生参数的等效原理图如图3所示。图中，电感 L1，L2，L3的寄生电阻分别是 rL1，rLa，rLb；电容 C1，C2的寄生电阻分别是 rC1，rC2，令rC1=rC2=rC；开关管的寄生电阻与寄生电容分别是rDs与Co；二极管的导通电阻和阈值电压为RF1，RF2，UFD1，UFD2；B为电路的电压增益；Seq为三相逆变桥的等效开关。在计算时我们假设输入电感电流纹波为零且等于输入电流Iin。

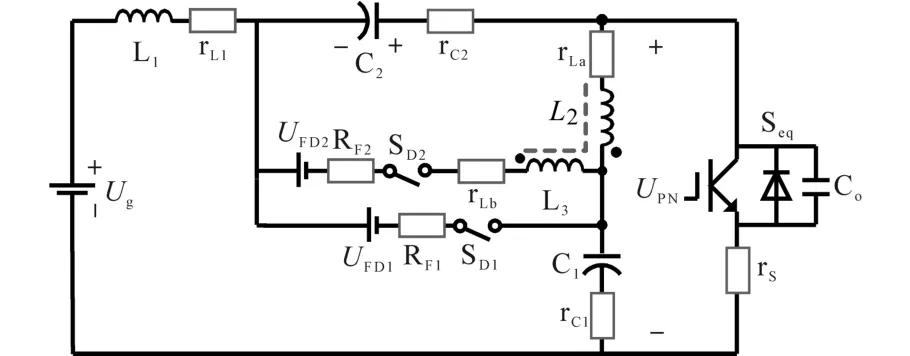
图3 有寄生参数下的等效电路Fig.3 Equivalent circuit with parasitic parameters

根据式（2）～式（7）计算的各电流与输入电流关系可得到各器件在直通与非直通状态下的电流。

2.1 开关管的功率损耗

开关管在直通和非直通的电流为

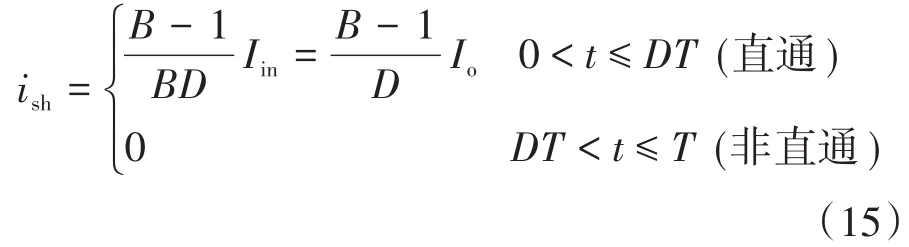
因此开关管在1个周期内的有效电流值为

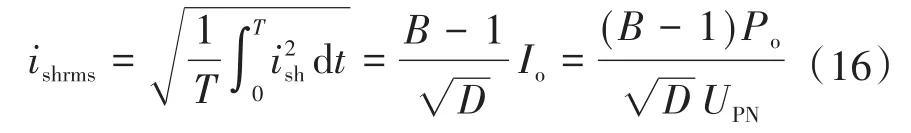
式中：Po为逆变器的输出功率。

由于逆变器有6个开关管，且直通时6个开关管处于同时导通状态，所以流经每相的电流等于1/3Ish，则逆变桥开关管总的导通功率损耗为

开关管关断损耗为

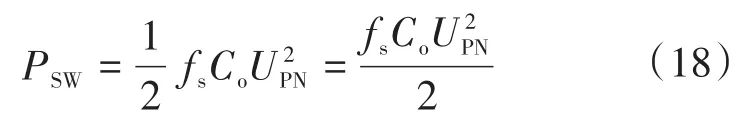
式中：fs为开关频率；Co为6个开关管的等效寄生电容总容值；CDE为逆变器中每个开关管的结电容。

于是可以得到开关管的总损耗为

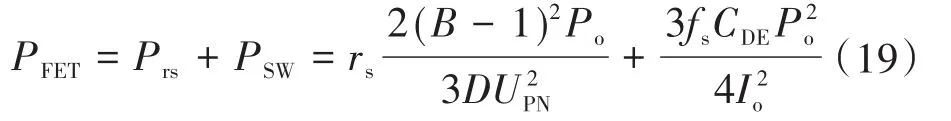
2.2 二极管的功率损耗

二极管在直通与非直通时电流值为

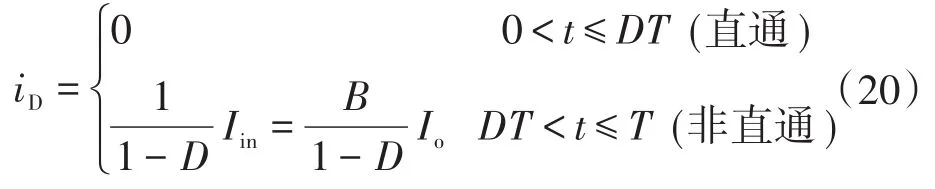
于是可以得到二极管在1个周期内的有效电流值IDrms和平均电流ID分别为

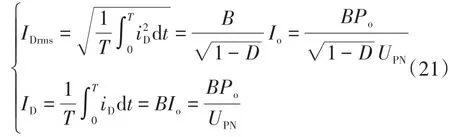
则二极管的导通损耗PRF和关断损耗PVF分别为

因此二极管的总损耗为

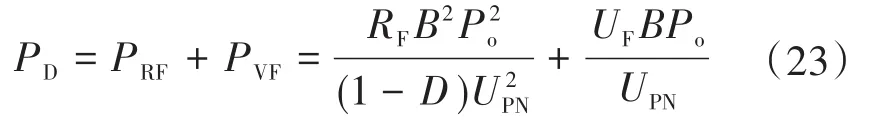
2.3 电感上的寄生电阻功率损耗

电感L1～L3直通和非直通时的电流值分别为

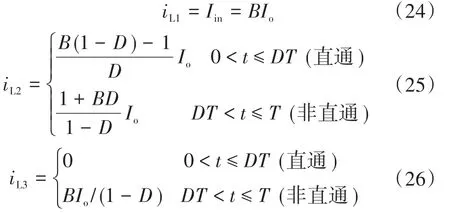
其中，电感L1两种状态下电流关系相同。由式（24）～式（26）可得到一个周期内电感上的电流有效值为

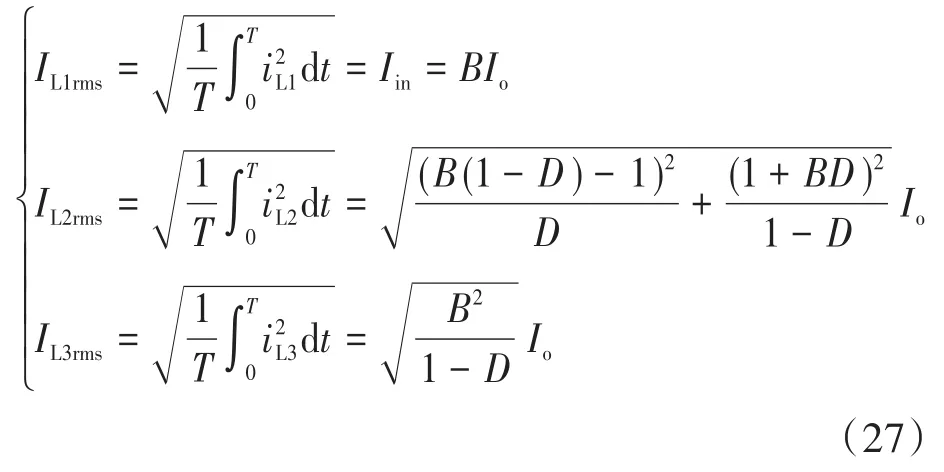
于是，电感上的寄生电阻功率损耗为

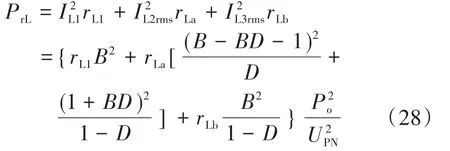
2.4 电容上的寄生电阻功率损耗

电容C1，C2上直通和非直通工作状态时的电流分别为

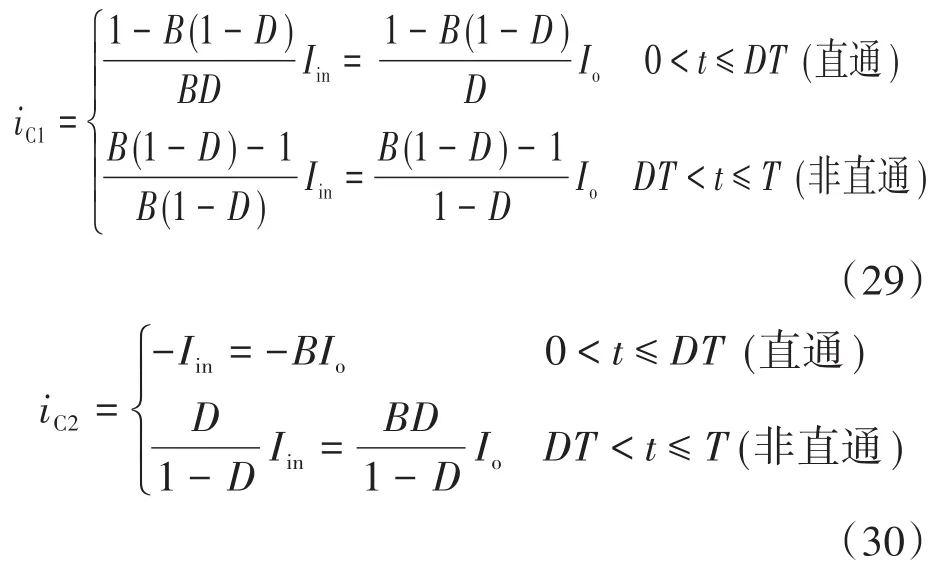
由式（29）、式（30）可以计算得到电容1个周期内的电流有效值为

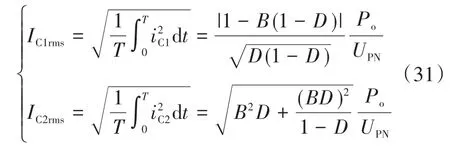
因此，电容上的寄生电阻功率总损耗为

2.5 电路总效率与分析

根据2.1～2.4节内容可得电路的总功率损耗为

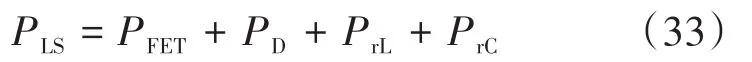
所以，有寄生参数影响下电路的效率可以表示为

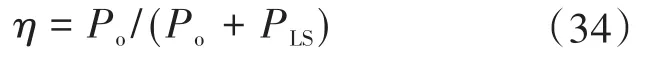
实验中实测的寄生参数值如表1所示，根据式（34）可以做出逆变器在有寄生参数影响下效率随输入功率变换的曲线图，如图4所示。图中选取耦合电感匝比N1∶N2=1∶2。

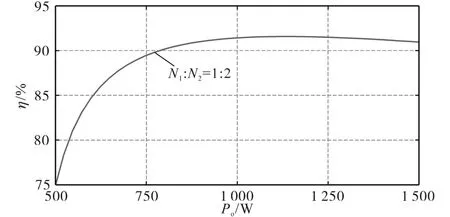
图4 效率分布曲线Fig.4 Efficiency distribution curve

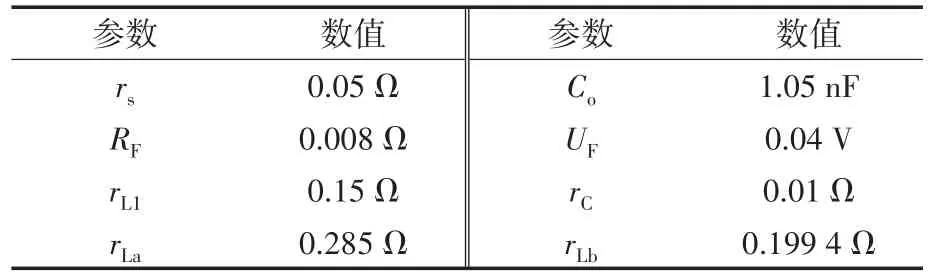
表1 器件寄生参数值Tab.1 Device parasitic parameter values

从图4可以看出，逆变器的效率随着输出功率的增大先增大又减小，在输出功率约为1 kW的时候效率会达到最大值。

根据本节推算出的各部分器件损耗可以作出其损耗饼图如图5所示，其中开关管损耗占了32%，二极管损耗占了10%，电感ESR损耗占了53%，电容ESR损耗占了5%。从图中可明显看出电感的寄生电阻对电路效率影响是最大的，其次是开关管的损耗，这就在提高电路效率方面有指向性的意义，即设计输入电感与耦合电感的时候从减小其寄生电阻入手，以及尽可能选择寄生参数小的功率开关管。

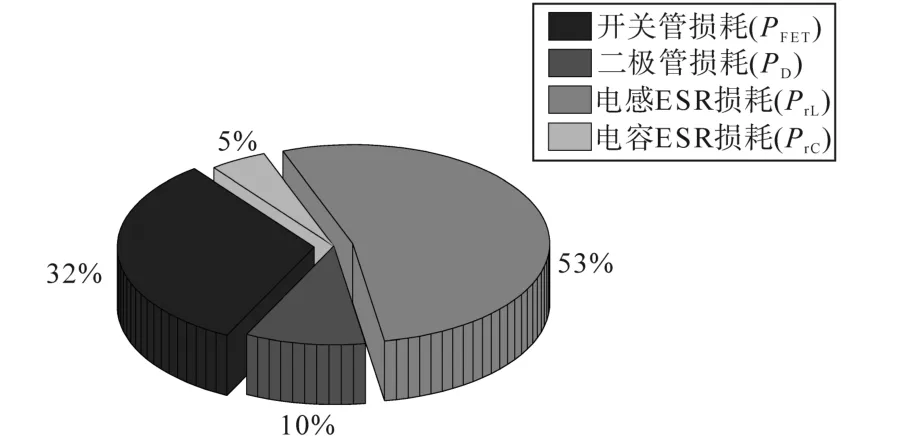
图5 效率损耗占比图Fig.5 Efficiency loss ratio chart

3 寄生参数条件下性能分析

由式（1）可知，理想情况下电路的电压增益B只与耦合电感的匝比n和逆变器直通占空比D有关，于是可以做出理想情况下升压因子分别与匝比、直通占空比的关系图如图6所示。

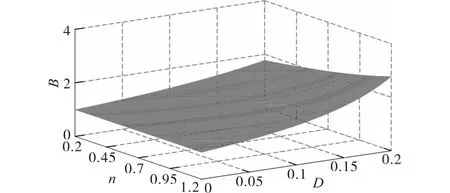
图6 理想条件下升压因子与匝比、占空比关系Fig.6 Relationship between the boost factor and the turns ratio，duty cycle under ideal condition

从图6中可以看出，电路理想情况下电压增益会随着匝比或者占空比的增大而增大，其中尤其以占空比在0.1～0.2之间时升压能力提升最为显著。

根据有寄生参数影响下电路增益表达式（12）可知，此时变换器电压增益不仅与占空比有关，还与各器件寄生参数值、负载等效电阻有关。图7为不同寄生参数下，电压增益与占空比的关系图，其中曲线（1）是将所有寄生电阻值设为0.1 Ω，匝比为2，负载等效电阻为30 Ω，剩下的曲线则是按图例逐一将一项寄生电阻值去掉，直至曲线（6）所有寄生电阻均为0。

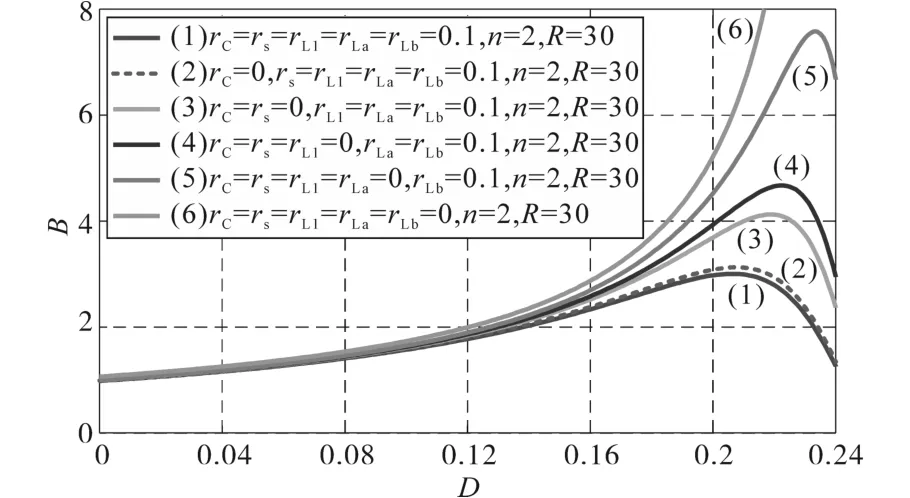
图7 不同寄生参数下电压增益与占空比的关系Fig.7 Relationship between voltage gain and duty cycle under different parasitic parameters

对比图7中曲线，可以得出：

1）理想情况下电压增益会随占空比增大到一定程度上出现极限升压倍数，占空比一定要在合适的范围内选取而避免这种情况出现，而在有寄生参数影响下，电压增益会在增大到一定程度后迅速被拉低。因此，电路设计时要确保其不会过大而引起系统性能降低以及发生安全隐患。

2）去掉电容寄生电阻值的曲线（2）与曲线（1）相比并无太大变化，可知电容寄生电阻对电路性能影响很小。

3）对比图中曲线的纵向差值，明显可以看出曲线（5）有最大的提升，其次是曲线（3），可知原边寄生电阻的减小对电压增益的影响最大，其次是开关管的寄生电阻。

根据式（14）可以绘制逆变器在有寄生参数影响下占空比与效率的关系图如图8所示。从图8中可以看出，电路效率在占空比小于0.12时降低的速度比较缓慢，大于0.12时效率加速下降，最后达到一定占空比之后就会急速下降，因此，选择占空比时不能超出一定范围以免影响效率。而从曲线纵向差值上来看，对效率影响最大的是原边电感的寄生电阻，其次是开关管的寄生电阻。

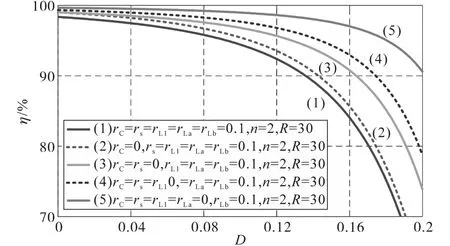
图8 不同寄生参数下效率与占空比的关系Fig.8 Relationship between efficiency and duty cycle under different parasitic parameters

4 仿真与实验结果分析

为了验证寄生参数对SCIqZSI电路的性能影响分析，用Saber软件分别在理想情况下和有寄生参数存在情况下进行电路仿真，并在实验室搭建功率达到1 kW的实验样机。实验及仿真过程中器件的寄生参数值见表1。表2为仿真与实验中变换器的各器件参数，其中L2k，L3k为耦合电感的漏感，fsh为开关频率，M为调制因子。为了方便操作，使用简单的SPWM控制策略对逆变器进行控制，实验样机使用TMS320F28335型数字信号处理器。

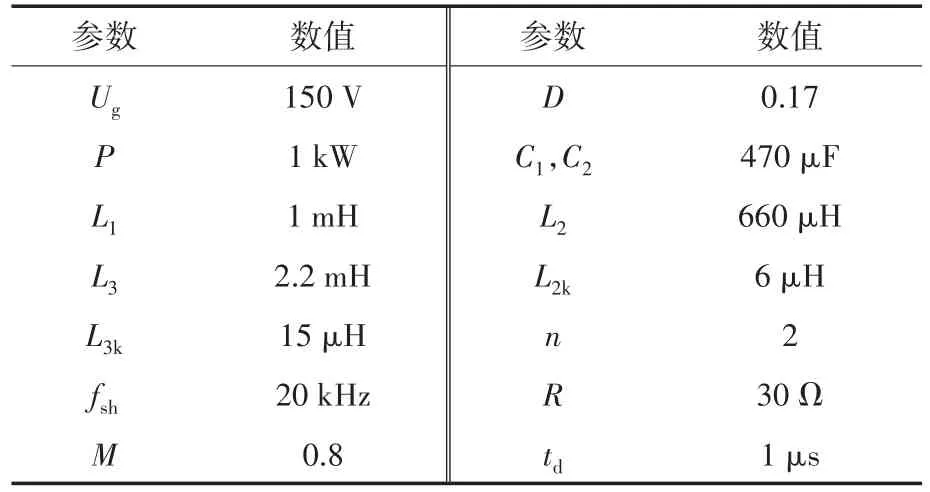
表2 样机仿真实验参数表Tab.2 Parameter table of prototype simulation experiment

图9为SCIqZSI电路在Saber中的电压增益仿真图，其中UPN1和UPN2分别为理想情况下与有寄生参数存在条件下电路的直流母线电压，Ug表示电路的输入电压。根据式（1）与表2中参数可知，理想情况下电压增益为3.125，UPN的值应该为468 V左右，而仿真结果中UPN1的值为457 V，这是由于仿真时使用的非理想器件造成的仿真结果存在一定误差，导致UPN1略低于理想状态下的值。而有寄生参数存在时的UPN2的值为405 V，此时的升压效率在86.5%左右，电压增益大幅跌落，可知寄生参数对电压增益有很大影响，验证了前面的理论分析。

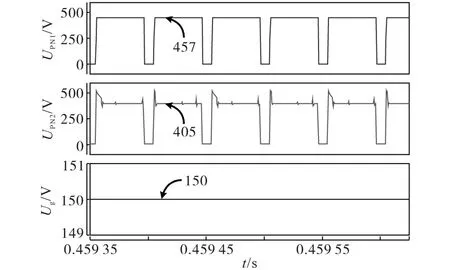
图9 SCIqZSI理想情况与有寄生参数存在情况下电压增益仿真图Fig.9 Voltage gain of SCIqZSI simulation in the ideal case and in the presence of parasitic parameters

在实验室对样机进行实验，变换器参数见表2，实验波形如图10所示，可以从图中看出样机的三相电压输出幅值在160 V左右，直流母线电压大约在400 V左右，与有寄生参数存在情况下电路仿真图及电路理论分析结果一致。

图10 SCIqZSI实验波形图Fig.10 Experimental results of SCIqZSI

分别进行了不同寄生参数下的实验验证。图11a是在不同输入电感和耦合电感寄生电阻rL1和rLa时的电压增益实测数据绘制图，验证了本文理论分析的正确性。随着占空比的升高，电压增益先升高到最高点后迅速下降。输入电感和耦合电感的寄生电阻降低了变换器的电压增益，而原边电感的寄生电阻的影响更严重。图11b则是在相同实验环境时对实验效率进行的实测绘制图。可以看出，电感的寄生电阻对变换器的效率影响很大，而耦合电感的原边电感寄生电阻对效率的影响更严重，与前面理论分析结果一致，验证了理论推导的正确性。鉴于此，在设计SCIqZSI电路时，对耦合电感要额外注意，尤其是耦合电感的原边绕组，在绕制的时候要采用优化的绕制办法以尽可能减少寄生电阻。

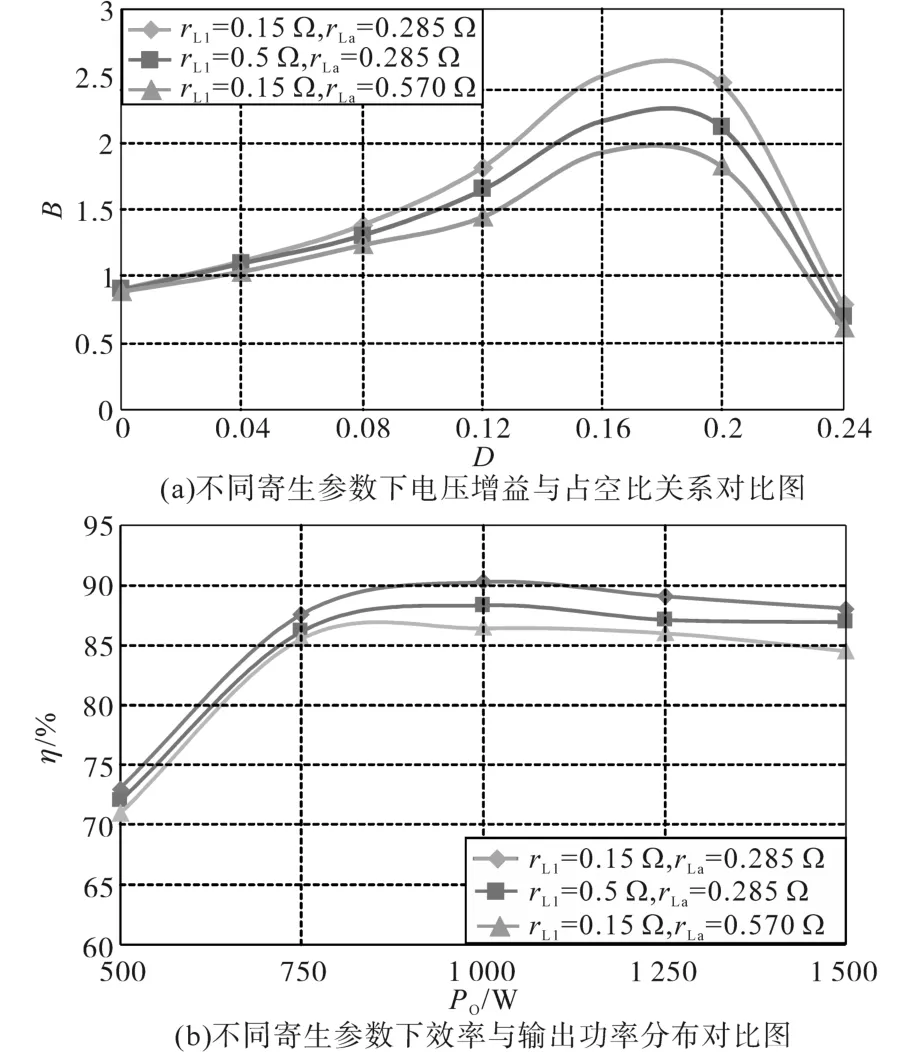
图11 SCIqZSI实验对比图Fig.11 SCIqZSI experiment comparison chart

根据实验结果可知，同等条件下，较大的寄生参数会对逆变器的效率产生负面影响，对该部分进行量化理论研究对逆变器的实际应用具有理论指导意义，可以从降低器件的寄生参数上来入手，提高逆变器的电压增益与工作效率，减小损耗，从而实现逆变器的最优化设计。

5 结论

文章对SCIqZSI逆变器电路中各寄生参数对系统效率的影响进行了公式推导与原理性计算，分析得到不同寄生参数对电路效率的不同影响程度，并在稳态下对含有寄生参数的电路进行研究，得到了有寄生参数情况下的电压增益和效率与直通占空比之间的关系。最后通过Saber对电路进行仿真并制作1 kW功率样机对理论分析进行验证，仿真与实验结果均验证了寄生参数对电路性能存在着极大的影响。新型变换拓扑的性能会随着拓扑中元器件寄生参数的适当减小而大幅提升，其中耦合电感、开关管的寄生参数效果最为明显。因此在样机的设计过程中，为了能够高效提升新型变换拓扑的综合性能，首选对电路影响程度比较大的元器件的寄生参数进行改良，比如用多股并绕及夹层绕法来制作耦合电感，选择寄生参数小的开关管等，为变换器性能优化与效率提升方面提供了方向。