基于VSG的直流侧混合储能自适应协调控制策略

丁权，王鲁杨，陈宇宁，黄河遥，余霄骏，白洪山

（1.上海电力大学电气工程学院，上海 200090；2.国网福建省电力有限公司泉州供电公司，福建 泉州 362000）

微网通过引入虚拟同步发电机（VSG）技术，使得传统逆变器具有同步发电机的惯性和阻尼，为大规模新能源友好并网、离网提供了新的技术手段[1-2]。

储能装置是微网不可缺少的部分，可减弱微网低惯性、抗干扰性差的劣势[3]。磷酸铁锂电池（后文简称锂电池）的能量密度高，但其功率密度较小；超级电容的功率密度较高，但其能量密度较小，结合这两种储能的优势，可提高储能系统的功率响应速度。文献[4]在不同惯性和阻尼参数条件下，分析了VSG的数学模型和控制策略，提出了可再生能源功率波动和储能系统功率分配的思路，同时给出VSG的储能单元优化配置的功率、能量和动态响应时间三大指标参数；但其仅给出单一的储能配置。基于大功率电池与超级电容组合的优势，文献[5]给出混合储能系统的功率分配控制策略，但未考虑到储能设备的荷电状态，可能会导致储能设备的过充过放，减少设备的使用寿命。文献[6]给出直流侧超级电容SOC和微网系统输出协调的控制策略；但其主源是柴油发电机，只限用于以孤岛运行为主的偏远地区且并未考虑分布式发电。

通过采用独立微网拓扑结构，以分布式发电为主电源，储能系统采用锂电池和超级电容组合，在VSG为微电网系统提供的惯性基础上提升了虚拟同步机的调频速度，同时引入自适应协调系数λ，实现超级电容SOC稳态工况下恢复其指令值（充放电裕度相等），保证了储能系统的安全、稳定运行；搭建仿真实验平台，通过对比分析验证了所提方案的可行性。

1 独立微网拓扑结构

仿真实验中采用的独立微网拓扑结构如图1所示。直流侧采用锂电池和超级电容混合储能装置，经双向DC/DC接至直流母线；可再生能源发电（renewable energy sources，RESs）在文中仅包括风力、光伏，两者均以MPPT控制经变流器接至直流母线；直流电经逆变器给负荷供电。

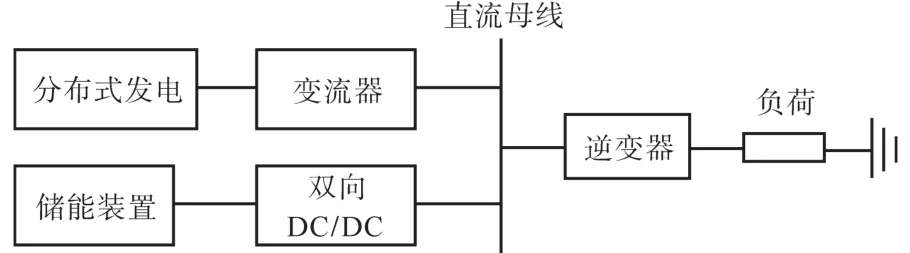
图1 独立微网拓扑结构图Fig.1 Topology structure diagram of independent microgrid

2 微电网内各单元模型建立及控制

2.1 VSG模型的建立及控制

同步发电机在任意时刻有转矩平衡方程如下：

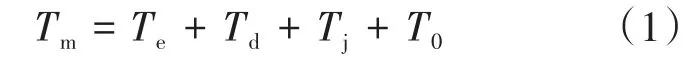
式中：Tm为机械转矩；Te为电磁转矩；Td为阻尼转矩；T0为空载转矩；Tj为转子变速转矩。

T0对应的空载损耗包括定子铜损、铁损、机械摩擦损等，其中一般主要指铁损。当Tm供以上各转矩仍有不足或余量时，则同步发电机的转子将加速或者减速，此差值为转子变速转矩Tj。虚拟同步机技术是通过数学建模模拟同步发电机的电气、转子机械特性。

主电路结构如图2所示，RESs可看作为原动机，混合储能系统可看作为同步发电机的转子部分。考虑虚拟同步机本身不存在铁损，可得VSG的机械方程如下：

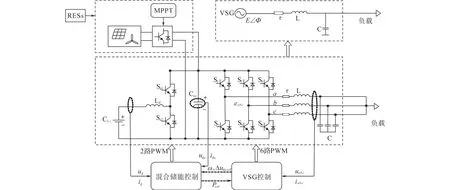
图2 含混合储能系统控制的VSG主电路结构图Fig.2 Main circuit configuration of VSG with modified control of hybrid energy storage system

式中：J为转动惯量；当转子极对数为1时，ω为系统电气角速度；ω0为微网的额定角速度；D为阻尼系数；Pe为VSG的电磁功率；Pm为机械功率。

Pm由有功给定值Pref和频率偏差响应指令值组成：

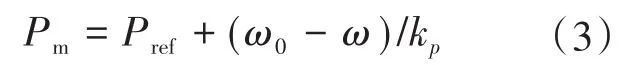
式中：kp为有功频率下垂调节系数。

图2中，eabc，uabc分别对应同步发电机的感应电动势和端子电压，L，r分别对应定子电抗、电阻。基于KVL定律可得VSG的电磁方程如下：

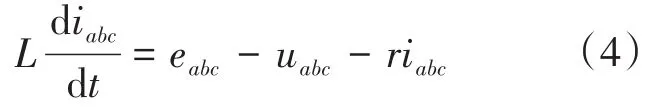
式中：iabc为同步发电机端子电流；eabc为由暂态电势E、输出功角ϕ构成的三相内电势。

暂态电势E包含VSG的空载电压E0与其无功调节输出Eq两部分：

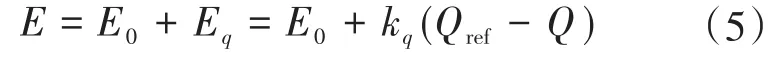
式中：kq为电压无功下垂调节系数；Qref，Q分别为逆变器输出无功功率的参考值和平均值。

结合式（1）～式（5）可得VSG控制策略如图3所示，通过采用电感电流内环和电容电压外环双环控制输出调制电压，并经过SVPWM调制输出6脉冲PWM信号。

图3 VSG控制结构框图Fig.3 Control structure block diagram of VSG

2.2 直流侧混合储能控制

将ΔPe定义VSG输出的电磁功率波动，即

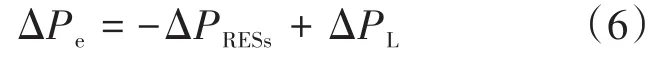
式中：ΔPRESS为分布式发电的出力波动；ΔPL为负载波动。

当∣ΔPe∣＞0时，微网系统频率会发生相应的波动，在逆变器上引入虚拟同步机技术可以快速、有效地实现频率偏差调节；同时通过对直流侧的控制，使得混合储能系统增发或吸收相应差值功率，实现微网系统功率平衡。锂电池、超级电容通过双向斩波构成的混合储能系统可实现差值功率的合理分配。

以下论述差值功率合理的分配问题。由式（2）可得[7]：

式中：Δω为电气角速度差。

等式左侧DΔω对应的是负荷调节功率，阻尼系数D的含义可表现为随频率升降单位负荷消耗功率变化的大小。等式右侧对应着储能系统的功率变化，其中ΔPm=-Δω/kp，由于调速器和系数kp的作用而变化较为平缓，故在文中称其为慢频功率；-Jω0·dΔω/dt为VSG虚拟转动惯量J引起的功率波动，正比于频率波动的变化率，该功率变化较为频繁，故在文中称其为快频功率。结合锂电池和超级电容特性可得功率分配公式如下：

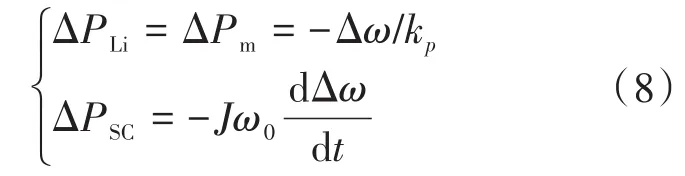
式中：ΔPLi，ΔPSC分别为锂电池、超级电容的功率波动。

当∣ΔPe∣＞0时，瞬间由超级电容释放或吸收差值功率，随后，锂电池CLi较为缓慢地对该差值功率进行吐纳，同时超级电容CSC减弱其缓冲作用，当系统达到稳态后，锂电池完全承担该部分差值功率，此时超级电容不参与功率交换。

图4为直流侧电压控制框图。

图4 直流侧电压控制框图Fig.4 Control block diagram of DC-side voltage

由图4可以看出，此控制是以直流侧电压为外环、以锂电池电流id为内环，构成电压电流双闭环，之后通过PWM调制得到2路PWM波。图4中udcref为直流侧电压指令值，为论述直流侧电压与系统之间的关系，引入直流侧电压波动指令值Δudcref，其定义公式如下：

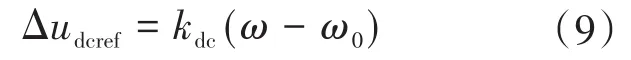
式中：kdc为直流侧电压调节系数。

微网系统频率会随ΔPe变化，当ΔPe＞0时，Δudcref随频率下降而下降，导致直流侧电压下降，进而CSC瞬时输出功率，待系统进入稳态时，CSC出力逐渐减小，锂电池出力逐渐增大，直至系统或直流侧电压完全稳定后，ΔPe差值功率由CLi补偿；当ΔPe＜0时，同理。

由电容能量计算公式，可得ΔPSC与直流侧波动电压的关系式如下：

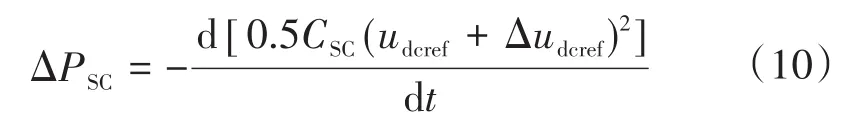
结合式（9）可得下式：

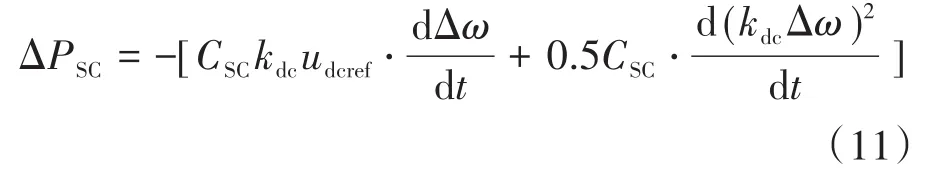
出于对VSG逆变的直流母线电压的稳定性和IGBT的耐受电压考虑，文中直流母线波动不应超过8%，即Δudcmax%=8%。从数值上比较，式（11）中的第1部分所占ΔPSC比重超过92%，可得结论：超级电容的交换功率差值与微网频率的变化率近似成正比，表明超级电容承担相应快频功率波动。

再结合式（7），可确定直流侧电压调节系数kdc的范围，如下：

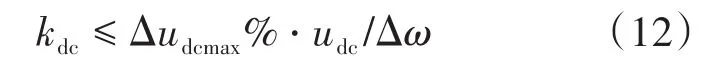
超级电容CSC的荷电状态SOC计算公式如下：

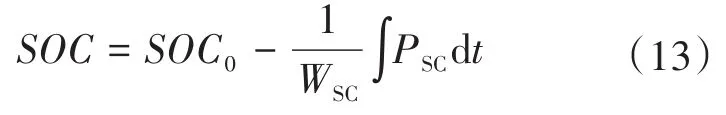
式中：PSC为CSC的放电功率；WSC为CSC的额定容量。

初始荷电状态SOC0计算公式如下：

式中：VSC，VSC_max分别为CSC的初始工作电压和最大允许工作电压。

实时SOC取值可根据式（13）、式（14）计算。

超级电容荷电状态的指令值计算如下式：

式（15）是取其工作允许的上限SOCmax、下限SOCmin的平均值，在SOC=SOCref时，CSC具有同等的充放电裕量。SOCmax，SOCmin的取值是由逆变器直流侧电压需求和CSC的额定电压决定的，结合某型号超级电容，取值为：SOCmax=80%，SOCmin=40%，即SOCref=60%。仿真实验采用5个该型号超级电容串联模块，单个具体参数如表1所示。

表1 超级电容参数Tab.1 Parameters of Cscmodel

3 VSG协调控制技术

考虑到锂电池的能量密度比超级电容的大得多，所以文中仅对频繁参与功率交换的CSC进行协调。

当ΔPe变化较大或者一直处于正、负增长时，超级电容的荷电状态SOC可能会处于不佳状态，甚至会处于过充过放的状态，不利于微网平滑过渡下次功率波动。参考电力系统一次调频原理，有功功率可根据频率偏差逆向补偿，进而改善微网电能质量[8]。为此引入协调系数λ，协调控制微网输出与超级电容的荷电状态，构成改进混合储能系统。协调控制策略表达式如下：

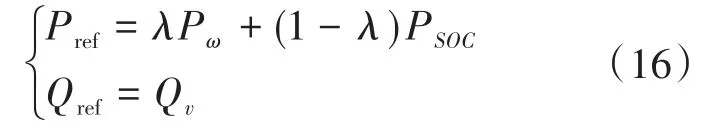
式中：Pω，PSOC，Qv分别为频率协调有功、SOC协调有功、电压调节无功。

由上段所述内容可得该三者的控制方程如下式：

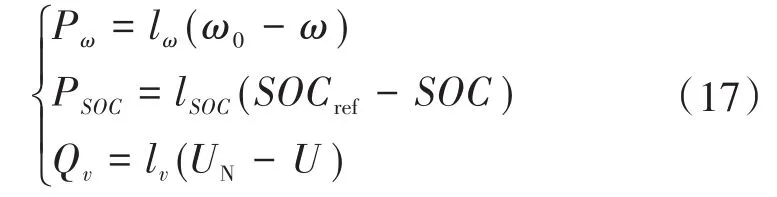
式中：lω，lSOC，lv分别为频率协调系数、SOC协调系数、电压调节系数；UN，U分别为VSG的额定电压幅值和端口电压幅值。

式（16）中协调系数λ的大小体现了VSG对微网输出与超级电容的荷电状态的协调偏向性，即对Pω，PSOC两者的协调能力是此起彼落的关系，其中VSG协调微网频率能力与λ取值成正比。自适应协调系数λ与SOC的关系表达如下：

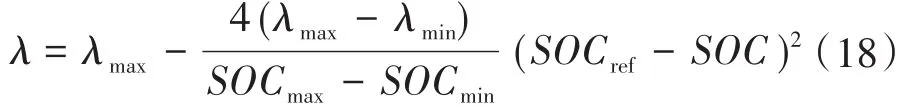
式中：λmax，λmin为自适协调系数的限值。

通过该算法，可实现：1）当超级电容SOC接近SOCref时，VSG可更多参与微网频率协调，快速恢复微网系统频率；2）当超级电容SOC接近SOCmax，SOCmin时，VSG需牺牲一定的频率协调能力，进行协调SOC，避免超级电容处于不佳状态，不利于平滑渡过下次ΔPe较大波动，甚至处于过充过放。λ与SOC的二次函数关系如图5所示。

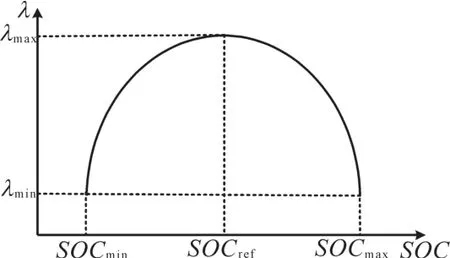
图5 自适应协调系数函数Fig.5 Adaptive coordination coefficient

为确定λ的取值范围，主要考虑该值和VSG的控制性能的关系。不计VSG无功和负载的影响以简化小信号模型，再结合式（2）、式（13）、式（17），可得该控制下的小信号模型，进而可得其特征方程如下：

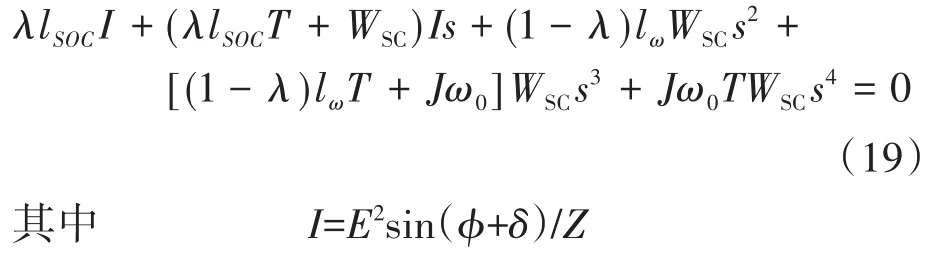
式中：Z∠δ为线路阻抗；T为滤波器时间常数。

通过分析系统的特征方程的根轨迹，综合微网系统动态响应速度和稳定性考虑，λmax，λmin两者取值分别为0.8，0.4，则λref=0.6。

4 系统仿真验证及分析

为了验证文中提出的控制算法，利用Matlab/Simulink搭建图1所示拓扑结构和控制算法的仿真平台。其中VSG额定功率为30 kW，开关频率5 kHz，仿真试验中所用重要参数如表2所示。

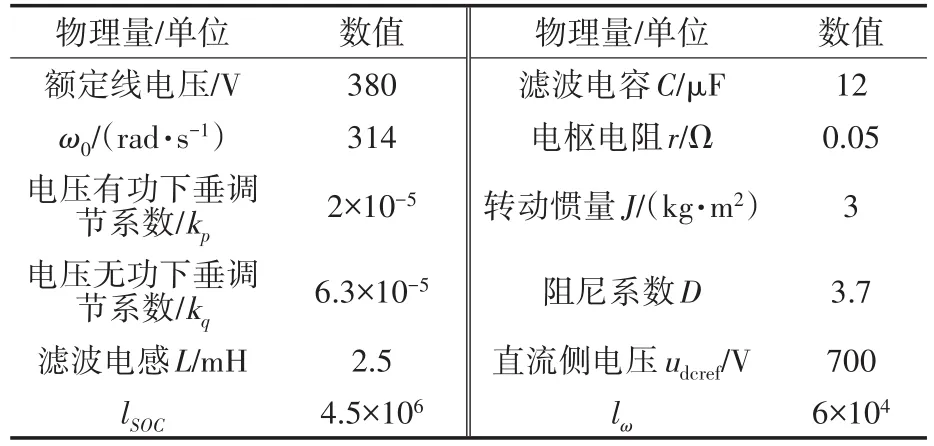
表2 仿真系统参数Tab.2 Parameters of simulation system

分别对ΔPe=0，ΔPe阶跃变化和ΔPe连续变化三种工况进行仿真并加以分析。

条件一：ΔPe=0。负载PL=5 kW，经VSG滤波输出的交流电压波形如图6所示，可见其峰值稳定在311 V，频率为50 Hz，可得出结论：提出的控制策略在负载恒定工况下适用性良好。

图6 交流侧电压波形Fig.6 AC output voltage waveform

条件二：ΔPe阶跃变化。t=4 s时，ΔPe=10 kW；t=8 s时，ΔPe=-10 kW。分别对A，B，C三组不同控制策略进行仿真分析，主要控制策略如表3所示。

表3 A，B，C三组主要控制策略Tab.3 Control strategy of paltform A，B，C

A，B，C三组的频率变化情况如图7所示，B组频率升降最小，Δf=0.1 Hz，且频率调节时间最短，Δt=0.68 s；C组下频率跌落差值为0.21 Hz，且频率调节时间为0.8 s；A组频率升降波动控制效果是三者中最差的，Δf=0.38 Hz。

图7 A，B，C三组的频率变化波形Fig.7 Frequency fluctuation of A，B，C

由于超级电容可瞬时平滑ΔPe波动，所以A组的Δf高于B组；对于C组，在超级电容瞬时平滑ΔPe波动的同时消耗了部分频率调节功率去协调超级电容的SOC，由上所述可得C组的Δf高于B组，且小于A组，三组Δf排序即A组＞C组＞B组。

图8为B组下的PLi+PSC+SOC变化波形。

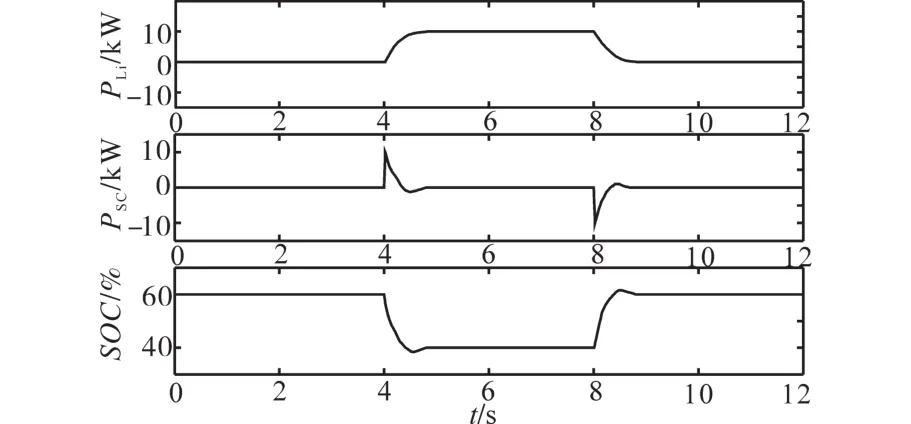
图8 B组下的PLi+PSC+SOC变化波形Fig.8 PLi+PSC+SOC fluctuation of situation B

观察图7和图8中第2栏的功率变化波形，在t=4 s和t=8 s时，可看出超级电容在0.06 s后出力达到10 kW、锂电池在0.6 s出力达到10 kW；对于A组来说，ΔPe阶跃变化时，由于锂电池的功率密度较小的特性，无法瞬时跟随功率变化，使得微网系统频率升降最大。

图9为C组下的PLi+PSC+SOC变化波形。

图9 C组下的PLi+PSC+SOC变化波形Fig.9 PLi+PSC+SOC fluctuation of situation C

结合图8和图9超级电容的出力、SOC变化情况，对比分析B，C两组。t=4 s时，超级电容瞬时出力后，C组出现一段负值功率，峰值为2.8 kW；t=8 s时，超级电容瞬时吸收功率后，C组出现一段正值功率，峰值为2.8 kW，这是由于C组在B组基础上引入了自适应协调系数，对系统频率和超级电容的荷电状态进行了“此起彼伏”的协调。

微电网采用C组控制策略下的具体情况为：∣ΔPe∣=10 kW的瞬间，CSC的SOC在SOCref附近波动，此时协调系数λ取值较大，系统更多参与到频率协调；当CLi输出功率变化跟踪上ΔPe时，SOC偏离SOCref较远，差值约为19%，此时协调系数λ取值较小，系统更多参与到SOC协调，与图9中超级电容出力瞬时变化后出现负值、正值的现象相吻合。另一方面也表明了系统是牺牲了一定的频率协调能力，因此系统频率调节时间会比B组更长，如图9中所示，当系统稳定后，C组超级电容荷电状态会恢复稳定在SOCref=60%，与理论分析一致，保证系统在稳态时超级电容具有相等充放电裕度。

条件三：ΔPe连续波动。为了检验该文提出的控制策略的适用性，在功率连续波动的工况下进行仿真与分析。

图10为C组下的ΔPe+PSC+PL变化波形。由图10可知：从t=2 s开始，ΔPe连续变化；超级电容承担快频功率波动（能快速的响应功率波动），锂电池在0.6 s延时后，跟踪上慢频功率。

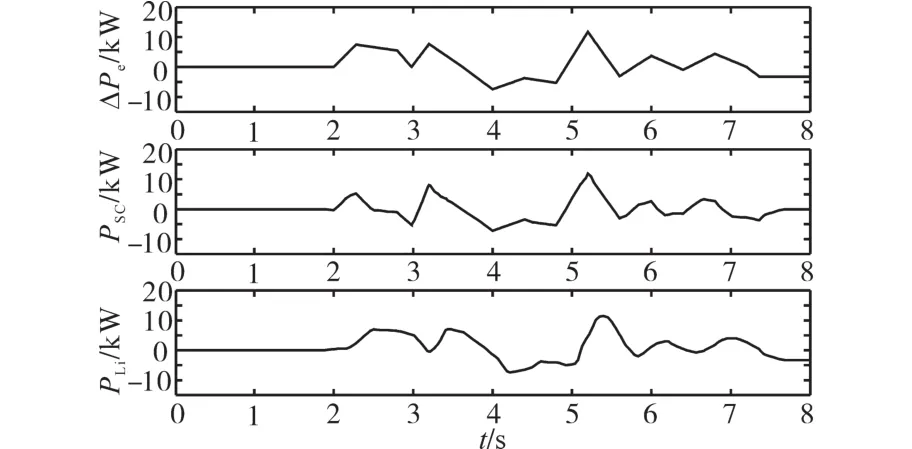
图10 C组下的ΔPe+PSC+PLi变化波形Fig.10 ΔPe+PSC+PLifluctuation of situation C

图11为C组下的SOC+udc变化波形。由图11可知，t=8 s时，ΔPe=0，超级电容SOC能快速的稳定在指令值上，与理论分析相吻合；第2栏所示为直流侧电压波动，在指令值700 V上下波动，ΔPe=0时，稳定在指令值，说明直流侧电压控制效果良好。

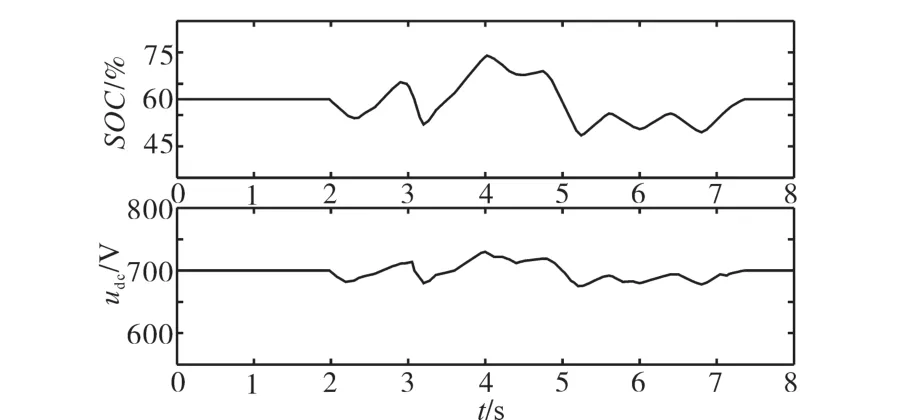
图11 C组下的SOC+udc变化波形Fig.11 SOC+udcfluctuation of situation C

5 结论

针对以新能源发电为主源的独立微网中，直流侧采用锂电池和超级电容混合储能的VSG控制策略进行了深入研究和仿真验证，得出如下结论：

1）文中将锂电池和超级电容的优点与VSG转子运动特性结合，通过控制直流母线电压且不依赖传统的高通、低通滤波器实现快、慢频功率的合理分配，有效地抑制了∣ΔPe∣变化时引起的微网系统频率波动，使微电网系统具有功率响应速度快的优点。

2）通过引入自适应协调系数λ，改进了VSG的指令功率，进而新增对超级电容SOC的协调控制，避免储能装置处于较差的运行状态；使微电网系统具有功率自适应协调能力，稳定性强的优点。