基于ZVS负载范围的移相全桥变换器参数优化设计

何俊鹏，张润泽，白旭峰，郝帅，曹虎

（中车青岛四方车辆研究所有限公司技术中心，山东 青岛 266000）

移相全桥变换器由于其超前和滞后臂的IGBT可实现零电压开通（zero-voltage-switch，ZVS），使其降低了开关管的导通损耗，提高了开关频率，减小了系统的体积和重量，提高了系统的转换效率[1-6]。因此，移相全桥ZVS变换器被广泛的应用于直流电源中。

然而在实际工程应用中，移相全桥ZVS变换器的参数设计却存在很大的困难。移相全桥参数设计的不合理将会导致ZVS软开关负载范围窄、工作效率低、占空比丢失严重等一系列问题，这都将影响系统的整体性能。因此，移相全桥ZVS变换器关键参数的优化设计十分重要。

目前国内外大部分学者更多的是侧重于研究移相全桥ZVS变换器的电路拓扑以改善其本身的缺陷，但针对其复杂的参数设计，大部分文献并没有系统地研究与分析[7-15]。文献[7]和文献[8]均是通过增加辅助谐振网络，使变换器的滞后臂可以实现更宽范围的ZVS。文献[9]提出了一种用耦合电感实现零电压零电流开关的移相全桥变换器，通过一个双绕组的耦合电感和两个二极管实现滞后臂开关管在宽负载范围的零电流关断。文献[11]提出了一种辅助电流可控的移相全桥零电压开关PWM变换器，可以在宽电压输入和全负载范围内实现一次侧开关管的ZVS。文献[13]和文献[14]在主电路拓扑结构上增加了一个磁芯，拓宽了变换器零电压软开关的实现范围，大大提高了轻载状况下的电源效率。这类方法既增加了电路的复杂性，同时也降低了系统可靠性。文献[15]针对移相全桥ZVS变换器，介绍了其工作原理并详细设计了谐振主电路关键元件参数，但是并没有定量分析谐振电感、IGBT死区时间等影响滞后臂ZVS的关键参数。

本文通过深入分析移相全桥ZVS变换器工作原理，推导出系统占空比丢失以及ZVS负载范围的数学表达式，并提出了一种基于ZVS负载范围的移相全桥变换器的参数优化设计方法。该方法将对移相全桥电路的设计具有十分重要的指导意义。

本文第1部分介绍移相全桥ZVS变换器的工作原理；第2部分基于ZVS负载范围，针对其关键参数进行优化设计，详细地介绍隔直电容、输出滤波电感、谐振电感以及IGBT死区时间的设计方法；第3部分通过搭建实验样机验证理论分析的正确性；最后对全文做出总结。

1 移相全桥ZVS变换器工作原理

图1为移相全桥ZVS变换器主电路结构图，其中，Q1～Q4为4个开关管，D1～D4和C1～C4分别为4个开关管的寄生二极管和寄生电容。Lr为谐振电感，Cb为隔直电容，Da～Dd为整流二极管，Lo和 Co分别为输出滤波电感和滤波电容。同一桥臂的两个开关管以180°互补导通，这里称Q1，Q3为超前臂，Q2，Q4为滞后臂。图2为移相全桥ZVS变换器的主要波形图。

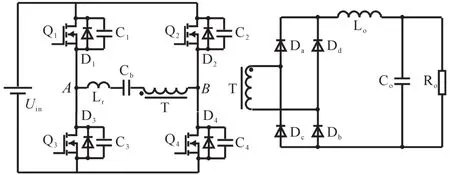
图1 移相全桥ZVS变换器主电路结构图Fig.1 Main circuit structure of phase-shifted full-bridge ZVS converter

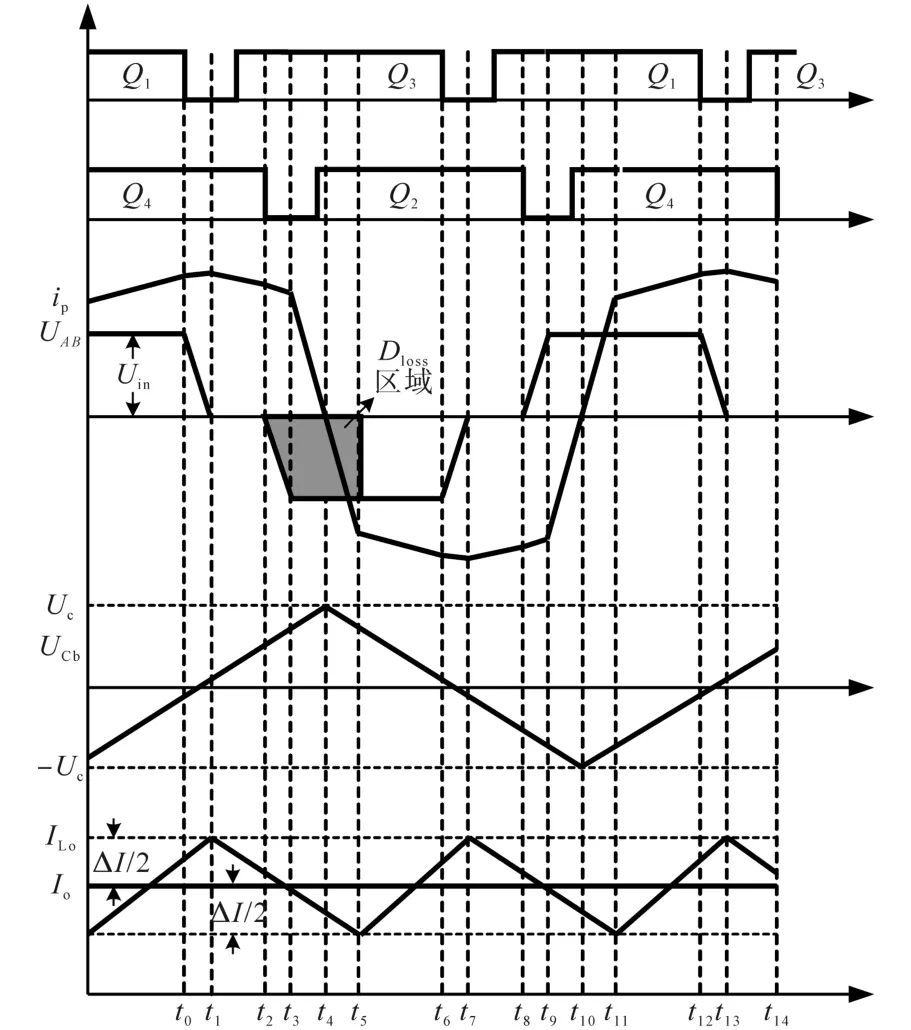
图2 移相全桥ZVS变换器的主要波形图Fig.2 Main waveforms of phase-shifted full-bridge ZVS converter

在1个开关周期内，变换器共有12种开关模态，由于其正负半周的对称性，这里只分析正半周6种模态。图3～图9为这几种模态下的等效电路，假设：1）所有器件为理想器件；2）C1=C3=Clead，C2=C4=Clag，其中Clead为IGBT超前臂并联电容，Clag为IGBT滞后臂并联电容。

模态0（0—t0）：如图3，Q1，Q4导通，原边电流ip流经变压器T、整流二极管Da和Db为负载供电。

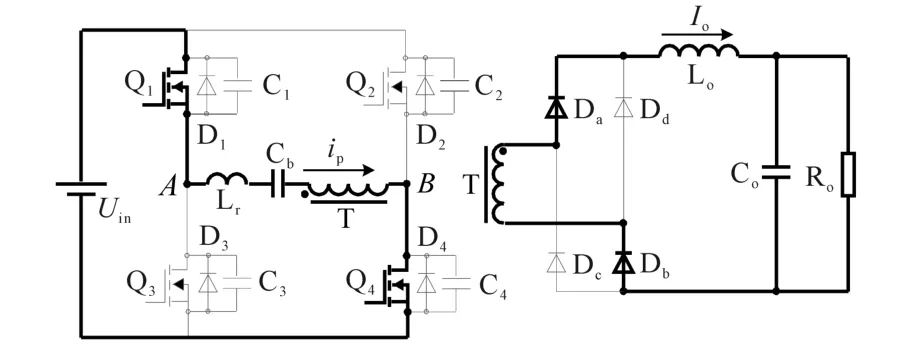
图3 移相全桥ZVS 0—t0时刻等效电路图Fig.3 Equivalent circuit of phase-shifted fullbridge ZVS converter in 0—t0

模态1（t0—t1）：如图4，t0时刻，关断Q1，此时C1充电而C3放电。电容C1电压从0上升至Uin，而C3电压从Uin下降至0。当C3电压下降至0时，D3自然导通。该模态内近似认为ip不变。

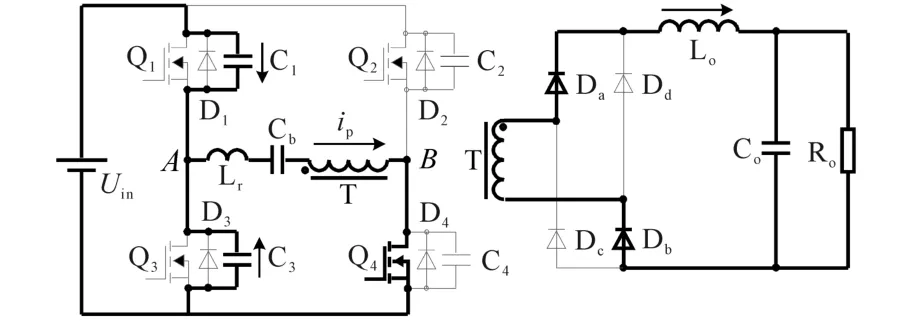
图4 移相全桥ZVS t0—t1时刻等效电路图Fig.4 Equivalent circuit of phase-shifted fullbridge ZVS converter in t0—t1

模态2（t1—t2）：如图5，D3导通后，Q3的漏源极电压被钳位在0，此时开通Q3实现零电压开通。但是由于ip方向未变，所以电流仍然流经D3。Q3实现零电压开通的条件为：Q1，Q3的死区时间必须大于模态1持续的时间，则有：

图5 移相全桥ZVS t1—t2时刻等效电路图Fig.5 Equivalent circuit of phase-shifted fullbridge ZVS converter in t1—t2

模态3（t2—t3）：如图6，在t2时刻关断Q4，此时C4电压从0上升，C2电压从Uin下降。原边电流ip减小，不足以提供负载电流。此时，变压器副边4个整流二极管均导通进入续流阶段。该模态内近似认为ip不变。

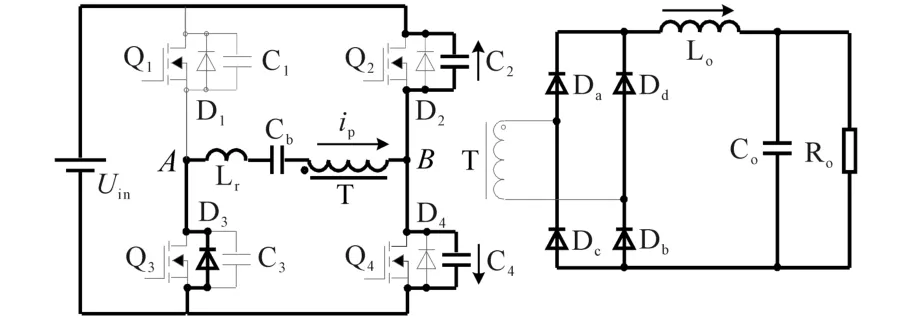
图6 移相全桥ZVS t2—t3时刻等效电路图Fig.6 Equivalent circuit of phase-shifted fullbridge ZVS converter in t2—t3

模态4（t3—t4）：如图7，在t3时刻，由于D2的导通，Q2的漏源极电压被钳位在0，此时开通Q2，实现零电压开通。但是由于ip方向未变，所以电流仍然流经D2。此时，变压器原副边并没有耦合，Uin电压全部加在Lr上，ip线性减小。当原边电流下降至0，D2和D3自然关断。

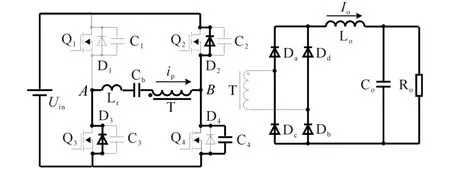
图7 移相全桥ZVS t3—t4时刻等效电路图Fig.7 Equivalent circuit of phase-shifted fullbridge ZVS converter in t3—t4

模态5（t4—t5）：如图8，t4时刻，ip过0并流过Q2和Q3，由负方向线性增大。t5时刻，ip增大至-Io（t5）/n，其中Io为输出滤波电感的平均电流，n为变压器原副边匝数比。此时变压器原副边耦合。Da和 Db截止，Dd和 Dc继续导通。

图8 移相全桥ZVS t4—t5时刻等效电路图Fig.8 Equivalent circuit of phase-shifted fullbridge ZVS converter in t4—t5

模态 6（t5—t6）：如图 9，在此阶段，Q2，Q3导通，ip反向线性增大，与输出电感电流Io呈匝数比关系。

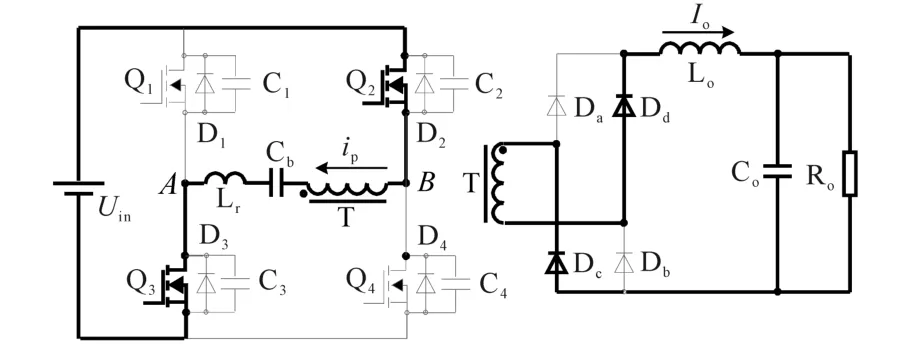
图9 移相全桥ZVS t5—t6时刻等效电路图Fig.9 Equivalent circuit of phase-shifted fullbridge ZVS converter in t5—t6

2 移相全桥ZVS变换器的参数优化设计

本节将基于ZVS负载范围对移相全桥变换器的关键参数进行优化设计，首先定义如下变量：系统容量P，输入电压Uin，输出电压Uo，开关频率f，IGBT超前臂并联电容Clead，IGBT滞后臂并联电容Clag。

2.1 变压器匝数比

移相全桥ZVS变换器输入输出电压关系可以表示为

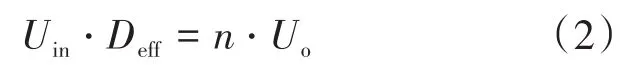
式中：Deff为系统有效占空比；n为变压器原副边匝数比。

在网压最低的情况下，系统的占空比丢失最严重，考虑系统能够接受的最大占空比丢失为Dloss，令此时Deff+Dloss=1，则变压器匝数比可以根据下式求出：

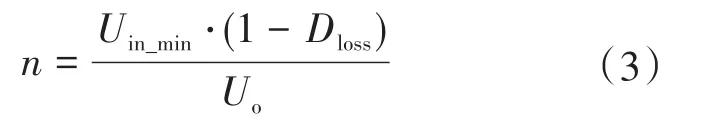
2.2 隔直电容

移相全桥ZVS变换器中隔直电容Cb的作用主要是防止变压器偏磁饱和，因此隔直电容的引入必须尽量减小对电路的干扰，一般取其电压峰值小于输入电压的5%。

由图2可知，变压器一个开关周期的正负半周原边电流会对隔直电容进行充放电。以原边电流的正半周为例，隔直电容电压从-Uc减小至0，又反向增大至Uc，原边电流的平均值可以根据变压器副边输出电流通过匝数比等效计算。因此，根据隔直电容上电荷变化量等式，则有：

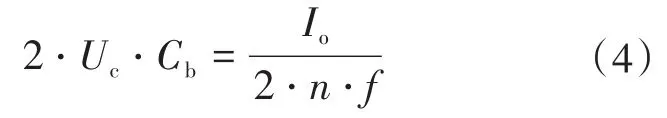
因此根据式（4），隔直电容可以求得：

2.3 输出滤波电感

输出滤波电感Lo的主要作用为与输出电容构成LC低通滤波器，可以滤除前端开关器件中的高频谐波。

如图2可知，在t1—t5时间段内，输出电感电流从Io+ΔI/2下降至Io-ΔI/2，输出电感电压近似为Uo，该阶段的持续时间可以表示为（1-Deff）/2f。根据输出电感的伏秒平衡原理可得：

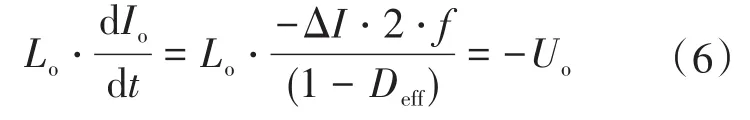
因此，输出滤波电感可以根据式（6）计算求出：

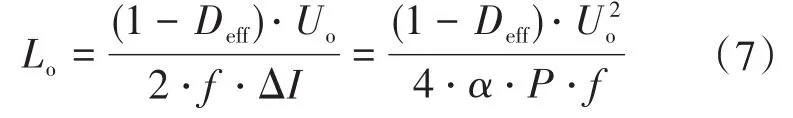
式中：Io为输出滤波电感的平均电流；ΔI为纹波电流峰峰值；α为纹波系数，认为ΔI=2αIo。

2.4 谐振电感

移相全桥电路中谐振电感Lr的主要作用就是配合滞后臂的死区时间，实现滞后臂的ZVS。但是，谐振电感的设计十分复杂，较小的谐振电感将导致系统滞后臂软开关范围窄、工作效率低；过大的谐振电感又将使得系统占空比丢失严重，变换器的输出电压不能得到保证。

由前文分析可知，在1个开关周期内，移相全桥电路占空比丢失时间即为t2—t5时间段。在此阶段内近似认为变压器原边电流ip呈线性变化，则有如下关系：

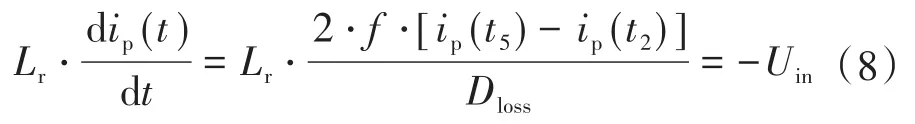
由于在t2，t5时刻，变压器原副边仍然存在耦合关系，因此这两个时刻的电流值可以根据输出电感的电流值折算至原边求得。

在t5时刻，ip所对应的变压器副边电流即为输出电感的波谷电流，其可以表示为

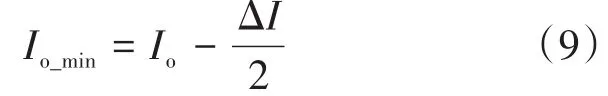
根据式（2）、式（7）和式（9）可以求得ip（t5）为

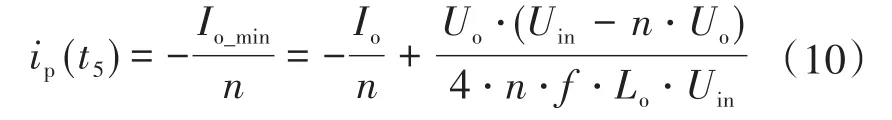
t2时刻输出电感的电流值仍然可以根据电流下降阶段的伏秒平衡原理求得，此时电流下降时间为占空比丢失时间，则有如下关系：

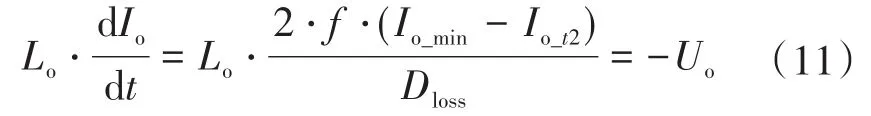
根据式（7）、式（9）和式（11）可求出ip（t2）为

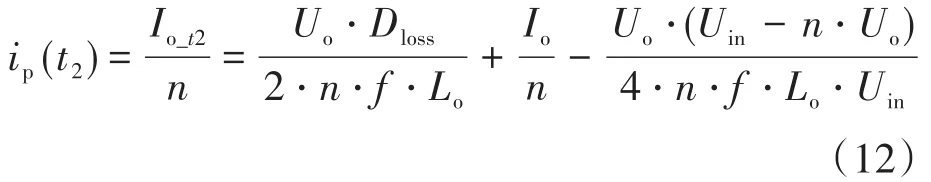
因此根据式（8）、式（10）和式（12），占空比丢失可以进一步求得：

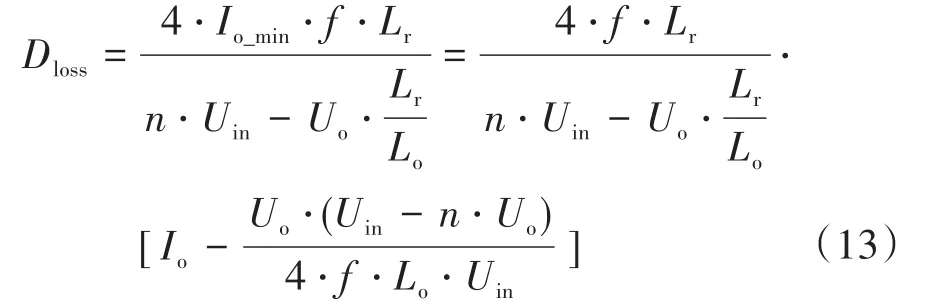
由式（13）可知，占空比丢失Dloss随负载电流Io的增大而增大，随输入电压的增大而减小。因此占空比丢失最严重的情况即为负载最大且输入电压最低工况下。在占空比丢失最恶劣情况下，系统若想仍然保证所需的输出电压就必须满足如下关系：

根据式（13）可以求得谐振电感的表达式，如下所示：

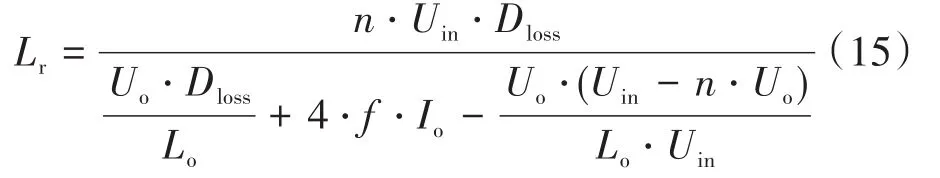
由前面的理论分析可知，滞后臂实现ZVS的条件为：t2时刻谐振电感存储的能量必须大于等于滞后臂并联电容完成换流过程所需要的能量，因此有如下关系式：

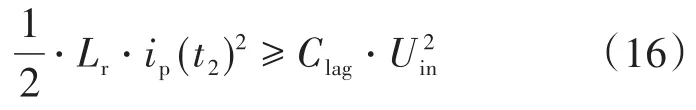
考虑能量相等的临界情况，将式（12）代入式（16），可求出谐振电感的表达式为

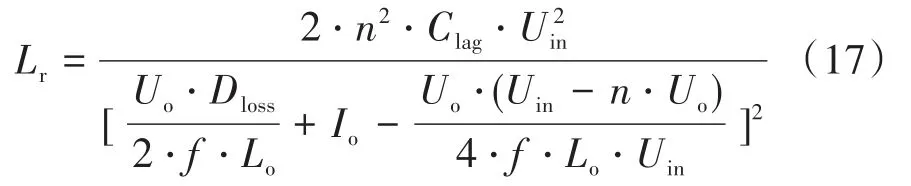
假设λ为负载系数，取值范围为0～1（例如：半载情况λ=0.5），Io代表满载时的负载电流，则在某一负载情况下，将式（15）和式（17）写成两个函数的形式，则有：

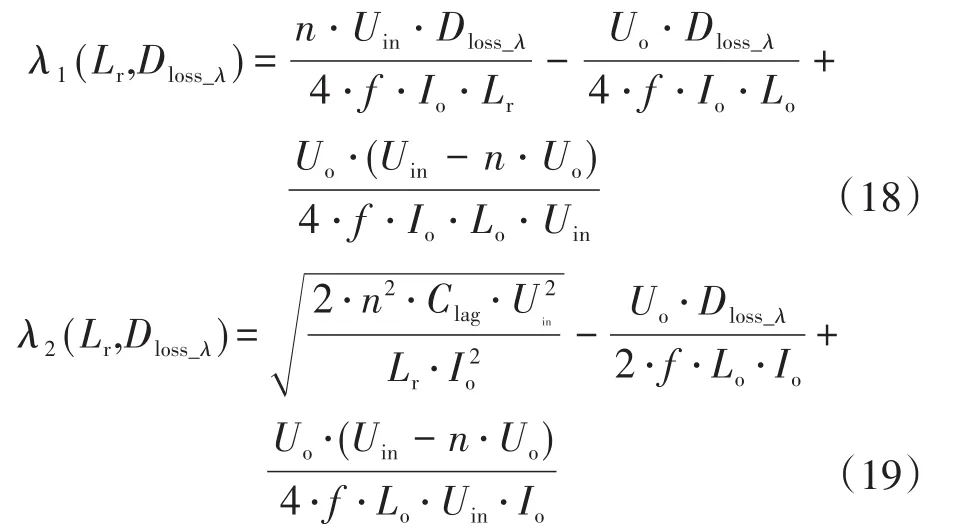
式中：λ1，λ2为因变量；Dloss_λ，Lr为自变量；Dloss_λ为λIo情况下的占空比丢失。

根据式（18）和式（19），画出λ1，λ2两个函数的曲面图，这两个曲面的交集即为该系统满足临界软开关条件所有点的集合，记为M（λ，Dloss_λ，Lr）。该集合表示的意义为：在已知参数条件下，当谐振电感选为Lr时，滞后臂实现ZVS的范围为（λ～1）Io，在λIo负载条件下的占空比丢失为Dloss_λ。

根据系统的散热能力，确定本系统实现ZVS软开关负载范围λ，在集合M（λ，Dloss_λ，Lr）中将该点提取出来。值得注意的是：在选取M（λ，Dloss_λ，Lr）集合中某一个点之后，需要验证在该谐振电感Lr的情况下，总占空比是否小于1，即式（14）是否成立。若不成立，需要适当减小谐振电感值进行重新选择，直至满足式（14）条件为止。

2.5 IGBT死区时间

为了使超前臂实现ZVS，需要使超前臂的死区时间满足式（1），to时刻的原边电流可以通过输出滤波电感波峰值折算值原边计算，因此超前臂死区时间可以根据下式选取：

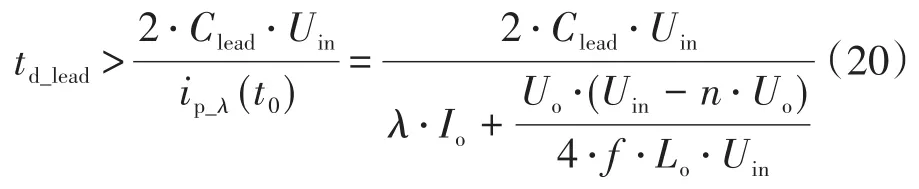
式中：ip_λ（t0）为λIo负载情况下t0时刻的原边电流。

滞后臂死区时间必须大于Q4断开后其并联电容Clag完成换流过程所需要的时间，则有：

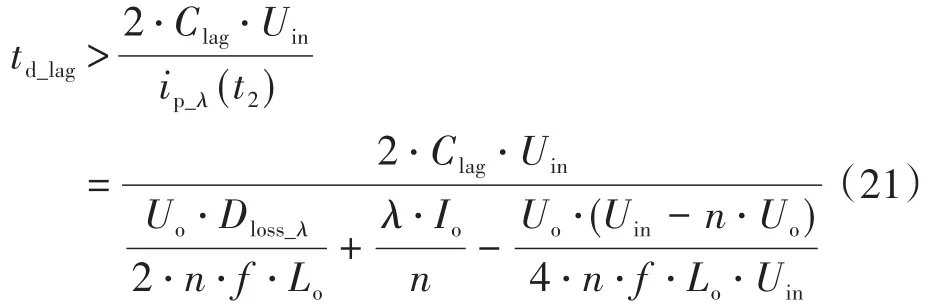
式中：ip_λ（t2）为λIo负载情况下t2时刻的原边电流。

同时，Q2应该在原边电流ip下降至0前开通，即Q2和Q4的死区时间应该小于原边电流ip下降至0所需的时间。原边电流ip下降至0所需的时间可以表示为

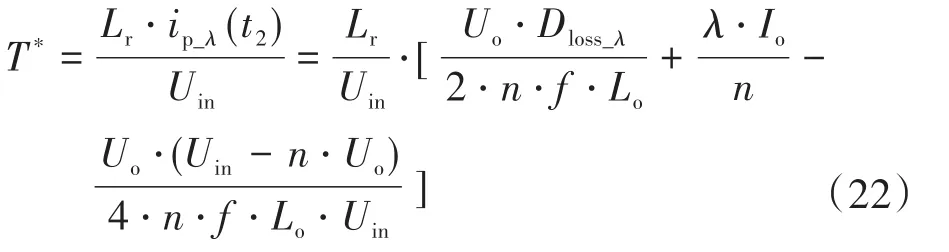
因此，根据式（21）和式（22）可知，滞后臂死区时间应该满足如下条件：

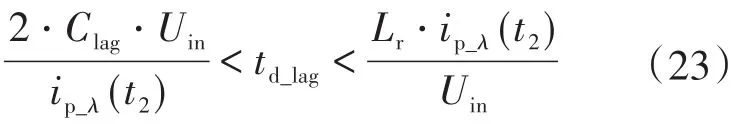
2.6 参数设计流程

综上分析，绘制移相全桥ZVS变换器关键参数优化设计流程框图，如图10所示。

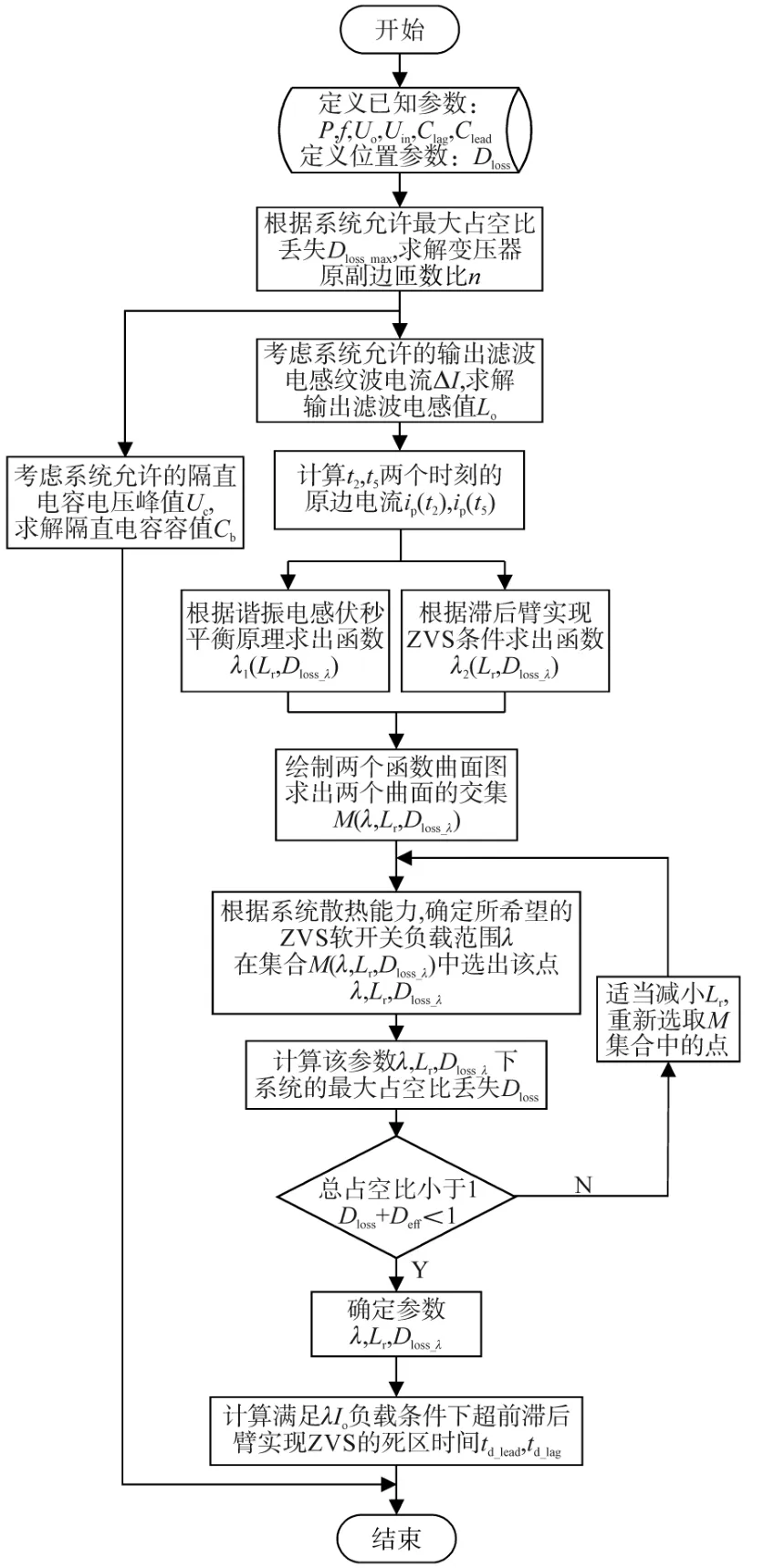
图10 移相全桥ZVS变换器关键参数优化设计流程框图Fig.10 Optimized design flow diagram of main parameter based on phase-shifted full-bridge ZVS converter

3 实验结果与分析

根据前文的理论分析，本小节将通过搭建45 kW的实验样机，验证其正确性。

表1为系统的电气参数。

表1 系统电气参数Tab.1 System electrical parameters

下面根据图10所示流程框图进行本系统的关键参数设计。

3.1 变压器匝数比

考虑在网压最低DC 500 V时，系统能够允许的最大占空比丢失为15%，则根据式（3）可以求得变压器原副边匝数比为0.7。为了降低副边整流二极管的电压应力，这里采用变压器副边双绕组型式，匝数比取4：3：3，等效匝数比为n=2/3。

3.2 隔直电容

考虑隔直电容的峰值电压Uc为输入电压的3%，则根据式（5）可以计算出隔直电容容值为84 μF，这里取Cb=80 μF。重新计算隔直电容电压峰值Uc=16.7 V。

3.3 输出滤波电感

考虑额定输入电压、10%满载条件下，输出滤波电感电流呈临界连续模式状态，即电感电流纹波系数α=0.1，则根据式（2）和式（7）可以计算出输出滤波电感值为485 μH，这里取Lo=400 μH。重新计算输出滤波电感电流纹波为ΔI=17.3 A。

3.4 谐振电感

系统的额定输出电流Io可以根据输出功率和输出电压求得：Io=P/Uo=71.4 A。将表1中的已知参数以及前文计算的n，Lo，ΔI代入式（18）和式（19），同时令Lr单位为μH，可以求得：

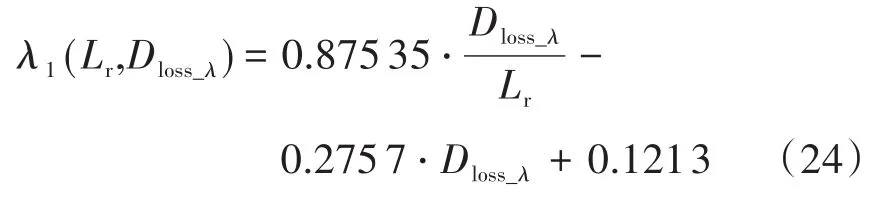
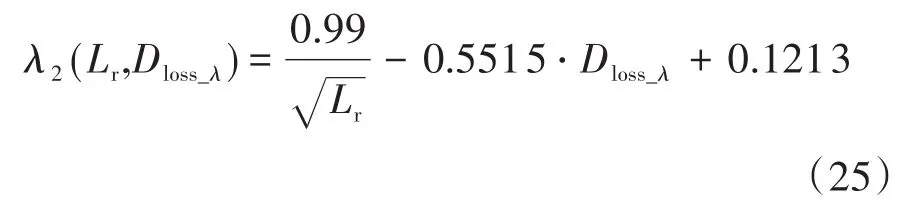
根据式（24）和式（25）绘制出两个函数的曲面图如图11所示。图11中深黑色空间曲线即为两个曲面的交线。根据本系统的散热能力，这里考虑ZVS软开关负载范围为40%，即λ=0.4。在空间曲线上选出相应的参数点M（0.42，10，0.03），该点的意义为：在已知参数下，谐振电感Lr选取10 μH时，系统可以实现0.42倍满载以上的ZVS，此时的占空比丢失为0.03。

图11 λ1和λ2函数的曲面图Fig.11 Surface plot of λ1and λ2function

最后通过计算在此谐振电感条件下系统的总占空比是否小于1，来验证参数选取的合理性。根据式（2）、式（13）以及式（14）可以求得有效占空比Deff、占空比丢失Dloss分别为 0.79，0.14，总占空比为0.93，满足小于1的条件，因此谐振电感参数设计合理。在此参数条件下，系统滞后臂实现ZVS的临界负载为45 kW×0.42=19 kW。

3.5 IGBT死区时间

为了使超前臂实现ZVS，需要使超前臂的死区时间满足式（20），可以通过求出不等式右侧的最大值来确定超前臂死区时间的范围。根据式（18）和式（19），当Lr=10 μH时，可以求出：DC 500 V输入电压条件下的λ=0.26；DC 750 V输入电压条件下的λ=0.42；DC 900 V输入电压条件下的λ=0.5。因此，不等式右侧的最大值可以计算为0.47 μs，这里取超前臂死区时间td_lead=1 μs。

滞后臂死区时间可以根据式（21）～式（23）进行选取计算。将已知参数代入式（21）求得其最小值为0.42 μs；同理，根据式（22）可以计算其最大值为0.56 μs。这里取滞后臂死区时间td_lag=0.5 μs。

综上分析，该系统的关键参数如表2所示。

表2 系统关键电气参数Tab.2 Key electrical parameters of system

下面搭建45 kW移相全桥电路实验平台，实验参数如表1和表2所示，实验结果如下：

1）在网压DC 750 V、输出功率40 kW工况下，观察系统隔直电容电压Uc和输出滤波电感电流ILo的情况，如图12所示。

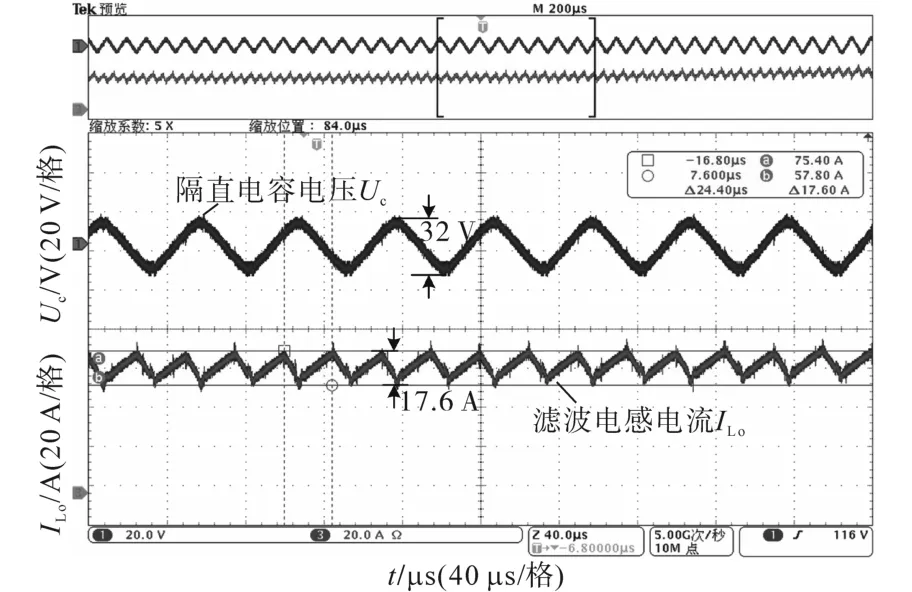
图12 网压DC 750 V、输出功率为40 kW工况下，隔直电容电压Uc和输出滤波电感电流ILo的实验波形图Fig.12 Test waveforms of Uc，ILounder the conditions of Uin=750 V and P=40 kW

由图12可知，隔直电容电压峰值Uc为16 V，输出滤波电感纹波电流ΔI=17.6 A。

2）在网压DC 750 V，输出功率40 kW、19 kW以及10 kW三种工况下，观察移相全桥滞后臂实现ZVS的情况，如图13所示。

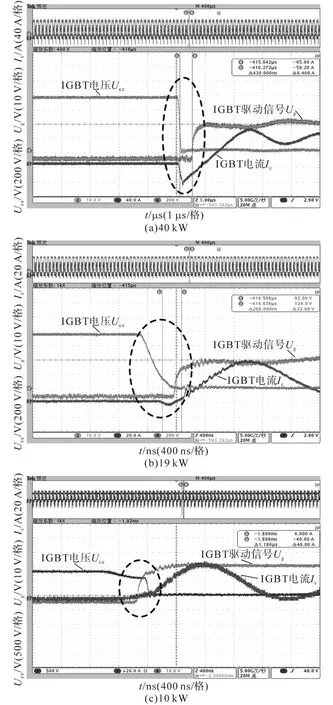
图13 不同负载下滞后臂驱动信号及电压电流实验波形图Fig.13 Test waveform of lag arm gate signal，voltage and current in different load

由图13可知：在负载40 kW时，滞后臂的并联电容电压下降至0后，经过一小段时间滞后臂开通，很好地实现了ZVS软开关；同理，在负载19 kW时，滞后臂的并联电容电压下降至0的时刻与滞后臂开通时刻基本重合，可以近似判断该工况下系统滞后臂处于临界ZVS软开关状态；在负载为10kW时，滞后臂在其并联电容电压下降至0之前就已经导通，因此该工况下滞后臂没有实现ZVS软开关。

3）在网压最低DC 500 V、输出功率40 kW时，观察移相全桥输出电压及占空比丢失情况，如图14和图15所示。

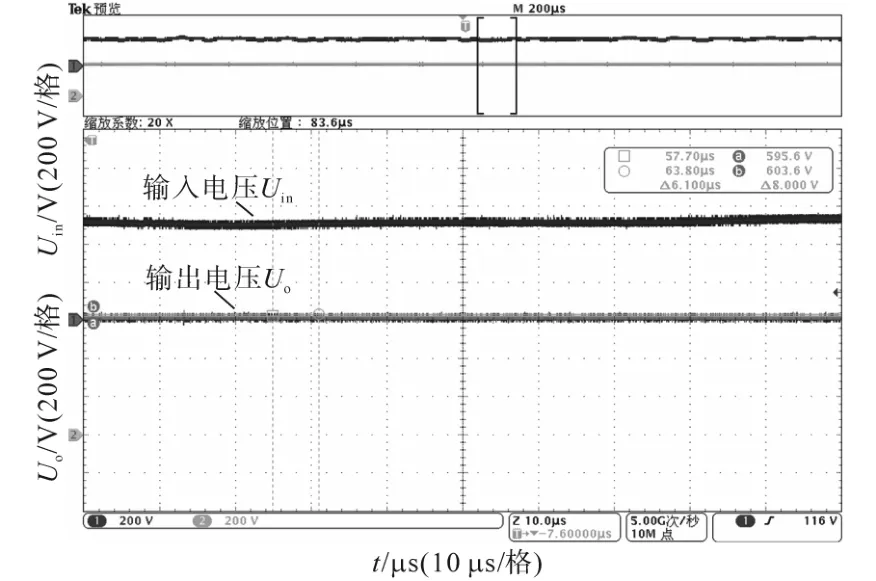
图14 输入电压为500 V、输出功率为40 kW工况下的输入、输出电压实验波形图Fig.14 Test waveforms of input and output voltage under the conditions of Uin=500 V and P=40 kW

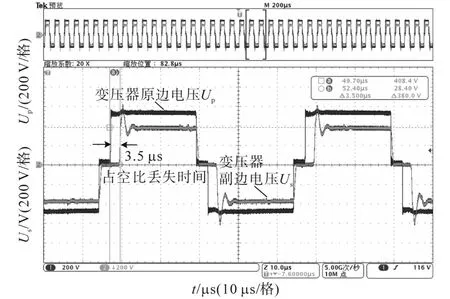
图15 输入电压为500 V、输出功率为40 kW工况下的变压器原副边电压实验波形图Fig.15 Test waveforms of primary and secondary voltage of transformer under the conditions of Uin=500 V and P=40 kW

由图14和图15可知，在输入电压为DC 500 V、输出功率为40 kW工况下，输出电压可以达到DC 600 V；同时占空比丢失时间为3.5 μs，占空比丢失为0.14。

综上分析，实验结果与理论分析基本保持一致，验证了理论分析的正确性。

4 结论

本文针对移相全桥ZVS电路复杂的参数设计问题，提出了一种基于ZVS负载范围的移相全桥变换器的参数优化设计方法。实验结果表明，该方法可以根据系统所希望实现的软开关负载范围，确定谐振电感、IGBT死区等关键参数的最优解，这将为实际工程应用中移相全桥的参数设计提供十分重要的指导与帮助。