隧道衬砌排水系统单元排水状态评价方法研究

魏晨茜， 蒋雅君, *， 刘世圭， 林利达， 肖华荣

(1. 西南交通大学土木工程学院， 四川 成都 610031； 2. 成都扬华源动新材料科技有限公司， 四川 成都 610213)

0 引言

近年来，我国隧道的发展速度不断加快，截至2020年底，全国铁路运营隧道里程为19 630 km[1]。由于地质水文条件复杂、设计施工规范性较差等原因，运营隧道中多数存在渗漏水现象[2]，影响隧道内人员行车与衬砌结构性能的安全。此类现象多数是由隧道衬砌排水系统出现病害后地下水无法顺畅排放所导致，进而影响其预期排水功能的实现[3]。

现阶段针对隧道衬砌排水系统及其病害的研究，主要集中在以下2方面。一方面是对运营隧道衬砌排水系统的病害类型及成因分析。蒋雅君等[4-5]总结出隧道排水系统的常见病害，划分为结构性病害与功能性病害2种类型并初步提出定性评估方法。蒋雅君等[6]、叶飞等[7]、郭小雄[8]从产生机制、处理措施等角度分别研究了国内隧道衬砌排水系统的结晶堵塞现象。另一方面则着重讨论隧道衬砌排水系统的优化构造，以期减少病害对排水功能的负面影响。黄骤屹等[9]建议设计管道时应充分考虑管道的抗压、抗变形等力学性能及管道内壁粗糙度等材料属性。肖明清等[10]建议增设仰拱底部排水系统、泄水管联通侧沟，通过横向排水盲管将侧沟与纵向排水盲管和中央排水盲沟联通。马伟斌等[11]设计出一种装配式衬砌排水系统，将纵向排水管、填充层排水盲管、仰拱底部排水盲管和检查井做成可拆卸的预制构件并相互连接。

上述研究均在不同程度上深化了对隧道衬砌排水系统的认识，前者分析了衬砌排水系统的病害类型及成因，后者引申出减缓病害、提高网络联通程度的构造措施，但总的来讲仍然缺乏有效的量化方法来阐述隧道衬砌排水系统的网络构造、病害影响以及与排水状态之间的互动关系，继而无法准确判断病害与优化措施各自对隧道衬砌排水系统的损伤或提升程度。

本文通过将隧道衬砌排水系统进行网络分层，并将隧道衬砌排水系统常见病害进行抽象处理，以衬砌排水单元为研究对象进行理论分析，旨在构建隧道衬砌排水系统单元排水状态评价方法，以期为隧道衬砌排水系统的优化提供参考。

1 隧道衬砌排水系统网络的基本概念

1.1 隧道衬砌排水系统的网络分层

常见的铁路、公路隧道衬砌排水系统主要由环向排水盲管、纵向排水盲管、横向导水管以及中央排水沟(管)等构件连接[12]，在隧道初期支护和二次衬砌之间形成排水网络空间，对地下水进行有组织的排放(见图1和图2)。

本文基于管道存在的空间位置、相互关系，将隧道衬砌排水系统网络按照结构分布和功能状态划分为宏观、中观、微观3个层面。

宏观层面主要包括能够承担完整排水功能的排水单元和排水系统，确保其综合多个组成构件最终形成相对独立的排水效果(见图3)。其中，排水系统由多个独立排水单元串联而成，而排水单元则是系统实现预期排水功能的最小有机整体。

中观层面主要由单元内各部分排水管段组成，表征完整网络与细部构造之间的承接关系(见图4)。单元排水功能的实现基于内部承担不同具体功能的多个管段。管段是单元内部细化后具有次级独立功能的完整个体，在整个排水管网中起到承上启下的重要作用。

微观层面主要是将单元内各管段细分为管节，认为一段完整管段是由若干管节组成，每个管节实体可抽象表示为由“节点-边”构成的数学模型(见图5)。这种划分方式的目的是将具有一定长度的管段做微分处理，以节点函数形式承载实体管节的排水信息。

图5 衬砌排水系统微观层面

1.2 隧道衬砌排水系统的网络属性

隧道衬砌排水系统的网络属性主要包括几何/材料属性、拓扑属性和水力属性。

1)几何/材料属性。隧道衬砌排水系统的几何属性主要包括管道坡度、管径、管段空间间距、管道长度、管道截面形式等参数；材料属性主要指各管段选用的具体材料的性能参数。可以说这2种属性共同决定了衬砌排水系统网络的实体特征，构成地下水流动疏排的实际载体。

2)拓扑属性。网络中不同节点与边之间的连接状态表征着节点之间关于地下水流动行为的传递关系。不同节点在网络中承担的作用不同，复杂程度更高的节点对网络整体功能的实现具有更大的重要度，因此可以用权重的形式加以描述。

3)水力属性。围岩中的地下水自围岩裂隙、缝隙渗入隧道衬砌排水系统网络，其分布路径类似河流，呈树枝状。地下水在排水系统网络中的流动一般依据高差，在重力作用下从高向低流动，可认为管道内部不承受压力(管道完全堵塞情况除外)，可通过研究网络内节点流量描述其水力属性。地下水作为悬浮物质极少的溶液，可认为其服从一般水流流动规律。因此，假定地下水为无压恒定均匀流或非均匀流。

1.3 隧道衬砌排水系统的病害类型

根据相关研究[4-5]，隧道衬砌排水单元的病害可分为结构性病害和功能性病害。结构性病害主要针对管道结构产生损伤或破坏，导致地下水流出管道；功能性病害主要指管道内过水断面受到影响的病害，该类病害并不破坏管道结构。

上述定义指出了2类病害的本质区别，但未提出规范的量化形式。为此，本文在结构性病害/功能性病害[6-7]的基础上将其典型病害划分为漏损和堵塞2类，部分调研实物图分别见图6和图7。

图6 漏损病害

图7 堵塞病害

2 衬砌排水单元的初始排水状态

衬砌排水单元的初始排水状态是指单元内部尚未发生病害时的完好网络所具有的排水状态，由排水功能阈值及其利用率表征。

2.1 排水功能阈值

作为衬砌排水单元的初始排水状态指标之一，单元层面关注的是平均排水功能阈值。而单元平均排水功能阈值可通过各节点的排水功能阈值加权得到，其间管段层面作为过渡阶段。

节点按照其几何属性的不同可分为直边圆管节点、直边方管节点和曲边圆管节点等形式，分别对应纵向/横向排水盲管、中央排水沟和环向排水盲管。

1)直边圆管节点。如图8所示，根据无压重力均匀流，代入谢才-曼宁公式可得其流量函数如式(1)所示。

(a) 直边圆管节点

(b) 圆管无压均匀流

(1)

式中：d为管径；i为管道坡度；n为管道内壁粗糙度；θ为过水包角；A为过水面积；R为水力半径。

求解式(1)极值可得θmax=1.68π，代入后得该节点排水功能阈值(最大理论流量)为6.76M(M为d、i、n组成的非水力系数，取值视实际设计参数而定)。

2)直边方管节点。如图9所示，根据无压重力均匀流，代入谢才-曼宁公式可得其流量函数如式(2)所示。

(2)

(a) 直边方管节点

(b) 方管无压均匀流

3)曲边圆管节点。如图10所示，环向盲管所处基底线型为隧道外轮廓多段弧线，管内虽未达到满流状态，但地下水的流动方向不断变化，底坡线、水面线与总水头线彼此互不平行，故可将曲边圆管内地下水视为恒定无压非均匀流体。

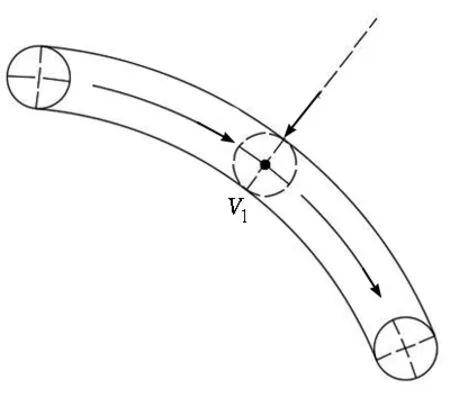
(a) 曲边圆管节点

(b) 圆管无压均匀流

假设环向排水盲管所处的隧道外轮廓线为对称圆形，取半径为R0。隧道纵向中线处为坐标原点，以水平向右、竖直向上为正方向建立坐标系，并取右半部分分析，如图11所示。设环向线上任意点与原点的连线与竖直z轴夹角为θ，取一微分弧段ds，对应微分角度为dθ，则有ds=R0dθ。设原点所在水平面为水位零点，现将微分弧段上按照明渠恒定非均匀流的特性构建水力模型，如图12所示。

图11 环向排水盲管右部坐标系

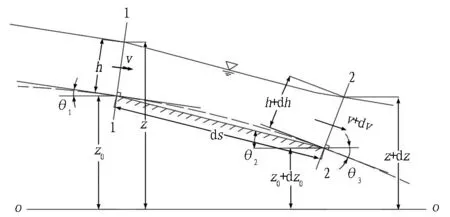
取断面1为上游断面，z0为该处基底水位，z为其实际水位，h为该处平均深度，v为其平均流速，θ1为断面1基底与水平面所夹锐角。θ2为所选弧段折线基底与水平面所夹锐角，ds为该弧段折线基底长度。取断面2为下游断面，z0+dz0为该处基底水位，z+dz为其实际水位，h+dh为该处平均深度，v+dv为其平均流速，θ3为断面2基底与水平面所夹锐角。

对该微分弧段列能量方程，如式(3)所示。其基本微分表达式如式(4)所示。

(3)

(4)

式(3)—(4)中：pa为管道内自由水面的大气压强；ρ为流体密度；g为重力加速度；α1、α2分别为断面1和断面2的动能修正系数，可令α1≈α2=α；hf为沿程水头损失；hj为局部水头损失；Q为管内中心节点的流量；K为流量模数；ζ为管道局部阻力系数。

根据水力学[13]可将式(3)—(4)处理后得式(5)，并以差分形式表示，则式(5)为隧道环向排水盲管曲边圆管节点内非均匀渐变流的排水功能阈值计算式。

(5)

式中Qj为环向排水管分节后任一节点排水功能阈值。

2.2 网络节点权重计算

传统衬砌排水系统单元有向网络如图13所示。此类网络节点的权重源于单元网络自身结构和功能方面的2种特性，因此,定义单一节点的权重由结构重要度和功能重要度构成[14]。

图13 传统衬砌排水系统单元有向网络

1)结构重要度。选取“介数”进行描述。介数是指所有经过该节点的最短路径占整个网络的有效路径之比，反映的是节点对整个有向网络的影响力，该值越大，表明节点在网络结构中的位置越重要。其计算公式如式(6)所示。

(6)

式中：i为管段编号；j为管段内节点序号；cij为经过i管段j节点的有效路径数量；c为单元内所有有效路径数量。

2)功能重要度。定义“出入数”进行描述。出入数是指某节点的所有入流功能阈值与其所有出流阈值之比，反映的是节点与周围直接连接的节点之间的流量聚散状况，该值越大，表明该节点在网络中起到的流量汇聚能力越大，反之则表明其分散能力越大。其计算公式如式(7)所示。

(7)

式中： ∑Qij,in-max为i管段j节点的入流阈值之和； ∑Qij,out-max为i管段j节点的出流阈值之和。

单元网络节点的权重γij可由节点介数uij与节点出入数λij相乘来表示：

(8)

2.3 功能利用率

排水管道的功能利用率是指当前实际汇入管道内的地下水流量对管道排水功能阈值的利用率，表征对管道预期排水功能的使用情况。

假设某排水单元共m个管段，每个管段划分n节，则节点功能利用率可由pij=qij/Qij,max表示。管段功能利用率如式(9)所示，单元功能利用率如式(10)所示。

(9)

(10)

3 衬砌排水单元的综合排水状态评价

衬砌排水单元的综合排水状态是指单元内部(可能)发生病害时的网络所具有的排水状态，由排水功能阈值、综合利用率和综合损失率表征。

3.1 病害的抽象形式与基本假定

隧道衬砌排水单元的病害主要表现为漏损和堵塞2类。由于排水管道的截面有圆形和矩形2种形式，同时管道具有一定长度，因此,病害的表现形式也与管道截面的几何形式有关。

1)漏损。漏损与管道截面形式之间关联不大，且由于沿长度发展的裂纹外形随机无规律，本文不展开具体讨论，参考SWMM流量分配原则使用等效替代作为抽象表示，如图14和图15所示。

Aij为节点ij截面的初始面积； Sij为节点ij截面发生的漏损等效面积。下同。

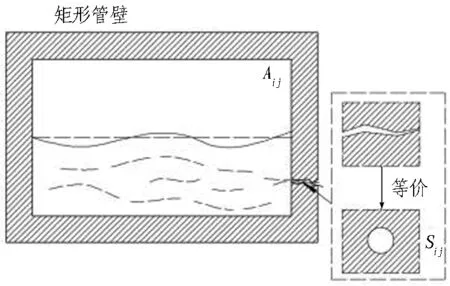
图15 方管节点漏损

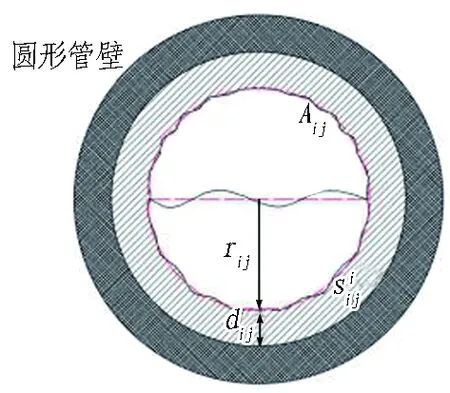
2)堵塞。堵塞与管道截面形式之间关联较大，且沿长度发展的堵塞形式有所不同，需要具体讨论。圆管和方管中按照堵塞产生形式和发育范围均可分为单点或多点离散堵塞(见图16和图17)以及多点连续堵塞(见图18和图19)。

(a) 剖面图

(b) 截面图

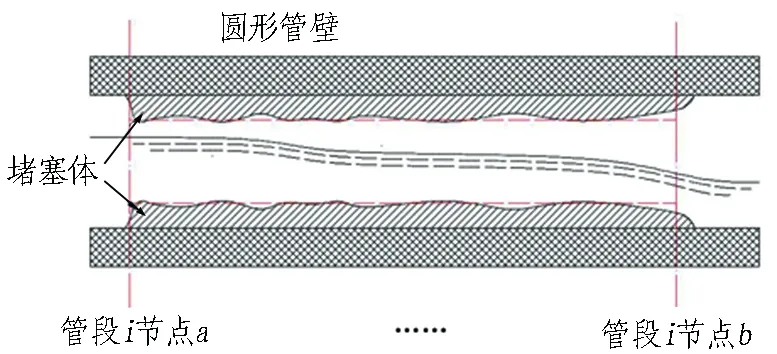
(a) 剖面图

(b) 截面图

(a) 剖面图

(b) 截面图

单点或多点离散堵塞体可使用无侧收缩矩形或月牙形薄壁堰假设。圆形管道内的多点连续堵塞体可使用环形堵塞体假设；矩形管道内的多点连续堵塞体可使用无侧收缩矩形宽顶堰假设。二者可通过改变排水功能阈值公式中的水力要素产生影响。

3.2 病害节点的排水功能阈值及利用率

(11)

(12)

式中：Qij,out-max为该节点的出流阈值之和，若为非交叉节点，则仅为该病害发生点所在的管道流量阈值；若为交叉节点，则为该节点所有出流管道的流量阈值之和。

由于漏损量与具体的漏损形式有关，预测难度极大，因此多依赖于实测数据。而堵塞造成的功能损失量正相反，很难实测，但可以通过理论公式进行推测。故对堵塞病害做进一步深化研究。

1)单点或多点离散堵塞[15]。矩形管和圆形管存在堵塞病害时的排水阈值计算分别如式(13)和式(14)所示。

(13)

(14)

式中：m0为流量系数，可取0.42～0.50；b为堵塞体的等效宽度；H为堵塞体等效高度；η0为管径修正系数，可取0.6～1.0；α和β为月牙形堰流经验系数，可根据CJJ 181—2012《城镇排水管道检测与评估技术规程》中划分的4级障碍物标准按表1取值，当实际障碍物处于两等级之间时，取更高级。

表1 月牙形堰流经验系数取值

2)多点连续堵塞。此时仍为明渠无压恒定均匀流假设，圆形管内可令现有实际管径rij=ηRij，现有粗糙度n′=n/τ，则功能损失量如式(15)所示，损失率同上。

(15)

矩形管可令现有过水面积Aij′=η1Aij，现有水力半径rij′=η2Rij′，现有粗糙度n′=n/τ，则功能损失量如式(16)所示，损失率同上。

(16)

3.3 综合排水状态的评价指标

衬砌排水单元的综合排水状态评价具有3个因子： 排水功能阈值、综合利用率和综合损失率。

1)排水功能阈值是指单元内所有节点的实际排水功能阈值在单元层面的加权求和值，表征现有单元排水功能的上限。

2)综合利用率是指单元内所有管段沿程的实际流量在整个单元全部管道范围内最大阈值中的占比情况，表征现有单元的使用充盈程度。

3)综合损失率是指单元内因病害导致的功能损失量在整个单元范围内初始功能阈值中的占比情况，表征管道内病害对单元排水功能造成的损失程度。

本文选用归一处理后的反正切函数综合3个指标因子，如式(17)所示。

(17)

4 算例说明

本文选用传统衬砌排水单元作为算例进行说明。纵、横向排水管均为φ110 mm HDPE双壁波纹管，坡度分别为0.3%和2%；环向排水管为φ50 mm HDPE双壁波纹管；中央排水沟为600 mm×600 mm钢筋混凝土矩形管，坡度为0.3%。病害单元算例如图20所示，其中每个管段划分5节，各节点、管段编号及实体位置对应关系如表2所示。

图20 病害单元算例

将传统构造单元的地下水流动路径以节点指向的形式表示： 1)N1→N4→N7； 2)N1→N4→N10→N8；3)N2→N10→N8； 4)N3→N6→N9；5)N3→N6→N10→N8； 6)N5→N4→N7；7)N5→N4→N10→N8； 8)N5→N6→N9；9)N5→N6→N10→N8。

传统结构单元节点重要性和权重计算结果如表3所示。

表2 传统构造单元有向图节点序号、段号与实体对照表

表3 传统结构单元节点重要性和权重计算结果

4.1 各管段排水功能阈值

1)纵向管：Qmax=0.001 3 m3/s。

2)横向管：Qmax=0.003 3 m3/s。

3)中央沟：Qmax=0.518 7 m3/s。

4)环向管： 根据水力学与水工学等知识[13]，可取(α+ξ)/2g≈0.1，并设环向盲管上节点过水断面面积以j2/n2的非线性形式变化，则右侧排水盲管各节点局部坐标及管节弧长如表4所示。

4.2 病害影响

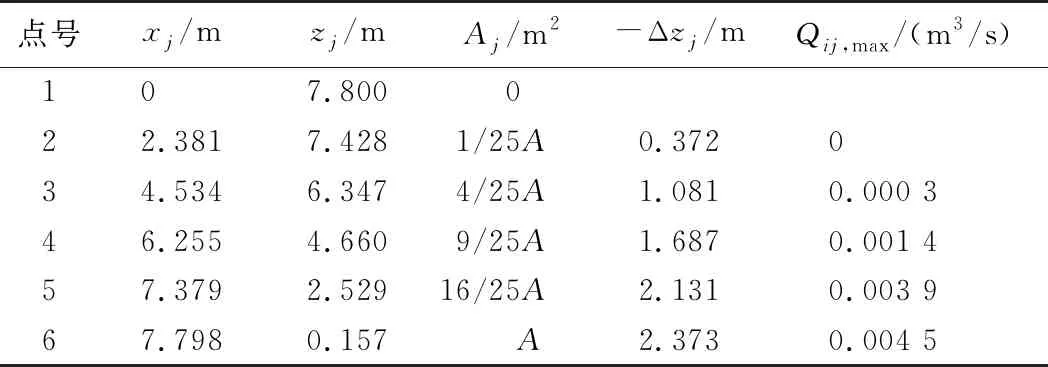
表4 右侧排水盲管各节点局部坐标及管节弧长

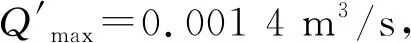
4.3 病害管段的综合排水状态指标

1)N1—N4(D1-4)段： 该段平均排水功能阈值Qmax=0.001 6 m3/s；管段综合损失率l=0.560×21.7%/5=2.4%；假设纵管平均利用率p1=100%，其综合排水状态指标s1=0.001 6。

2)N4—N10(D4-10)段： 横管的平均排水功能阈值Qmax=0.002 8 m3/s，此部分横向排水管段的综合损失率l=(0.560+0.222×4+0.563)×57.7%/5=23.2%，假设纵管平均利用率p1=100%，其综合排水状态指标s2=0.002 3。

由此可见，在此种情形下，横向排水管段的综合排水状态好于纵向排水管段。

4.4 单元的综合排水状态指标

经计算，各段平均排水功能阈值如下。

1)上游左侧纵管：Qmax=0.001 6 m3/s。2)上游右侧纵管：Qmax=0.002 2 m3/s。3)下游左侧纵管：Qmax=0.001 4 m3/s。4)下游右侧纵管：Qmax=0.001 4 m3/s。5)左侧横管：Qmax=0.002 8 m3/s。6)右侧横管：Qmax=0.006 6 m3/s。7)左侧环管：Qmax=0.004 m3/s。8)右侧环管：Qmax=0.004 m3/s。9)中央水沟：Qmax=2.021 9 m3/s。则单元整体的排水功能阈值为：Qmax=0.041 m3/s。而单元的综合损失率l=[0.560×21.7%+(0.560+0.222×4+0.563)×57.7%]/(10×5)=(0.121 5+1.160 3)/50=2.6%。

假设该单元各管段、节点均完全利用，即p均为100%，则该单元的综合排水状态指标s=0.040 3。

5 结论与展望

本文通过调研及理论分析，将隧道衬砌排水系统单元网络的病害形式、排水状态实现量化评价，并设置算例加以说明，得到以下结论：

1)隧道衬砌排水系统网络可按结构分布和功能状态划分为宏观(单元/系统)、中观(管段)、微观(节点)3个层面。该网络具有几何/材料、拓扑和水力属性。管道内地下水的流动状态视管道几何属性可选无压恒定均匀流或渐变流假定。

2)提出了排水功能阈值、综合利用率等的概念及计算方法，量化了初始排水状态的理论最大功能和管道排水功能的实际利用程度；提出漏损/堵塞病害的抽象形式，给出排水功能损失率的定义及计算方法，量化了管道受病害的影响程度。

3)提出了适用于隧道衬砌排水单元网络的权重计算方法，并构建综合排水状态评价指标s的概念及其计算方法。设置算例进行阐述，结果表明此种病害情况下该单元综合排水状态指标s=0.040 3，实现了衬砌排水单元综合排水状态的量化评价。

当前隧道衬砌排水系统量化评价方面的研究处于起步阶段，虽然本文构建出衬砌排水单元的量化评价模型，但还需要在下一步研究工作中继续讨论不同构造设施及维护措施对其排水功能及排水状态的量化影响，进而完善隧道衬砌排水系统的量化评价体系。