环状给水管网自动生成树的研究

赵星明，王 萱

(山东农业大学水利土木工程学院，山东 泰安 271018)

城镇给水管网的投资占整个给水工程比例较大，因此其最优化设计一直受到重视。最优化设计的前提是对环状给水管网的管段流量确定初分配方案，若给水管网的规模较小，可通过分析控制点位置以及大用户的分布，确定主干管供水路线，较合理地分配管段流量。对于中等以上的城市，仅依靠主观判断分配给水管网的管段流量会造成较大误差，不能满足用户的实际用水量，也不能实现最优化设计。

初始流量分配可以采用最小平方和的流量分配法和截面法等，最小平方和法分配的管段流量比较均匀而使管道主次不分，截面法分配的管段流量不能满足节点流量平衡的条件。若采用图论理论把环状给水管网中的若干条管段删除，生成树后再进行初始流量分配，可符合节点流量连续性方程。把管网图化为生成树，须按照欧拉公式删除与基环数一样多的管段来破坏所有的环，并保持原管网的连通性，对一个规模较大的环状给水管网，仅靠主观判断生成树需花费很多时间。

本文根据Kruskal算法对环状管网生成树问题进行研究，利用带权重的邻接矩阵得到了最小生成树，并在AutoCAD平台上运用深度优化搜索方法，实现了删除连枝自动生成树，可方便管段初始流量的计算，提高环状给水管网的设计计算效率和准确度。同时，通过人工干预保留一些管段流量易确定的连枝，以优化环状给水管网布局。

1 环状给水管网生成树的方法

一个连通管网图G(V，E)，由N节点和M管段构成，V和E为节点和管段的集合，根据图论理论计算其内环数L=M-N+1。若想把G(V，E)生成一棵树需删除与内环数相等的L条管段，删除的管段称为连枝，保留下来的管段称为树枝。在环状给水管网的工程设计中，连接管和末端管主要承担本段沿线流量的分配，流量容易确定，可作为连枝删除掉，一部分管段流量不易确定的主干管和转输管等作为树枝保留下来，这些树枝的管段流量可在生成树管网图上通过节点连续性方程求出。为了保留重要的主干管和转输管，把管网图G(V，E)转化为一个加权图G(V，E，W)，W为管段权重Wij的集合，在此假设想保留下来管道的Wij=1，其权重最小，而其他管道的Wij>1，管道的权重越大越容易被删除。需注意的是权重大于1的管道比需删除的管段数L要多，所以权重大于1的管道不会全部删除，也要保留一部分，哪些管道保留下来或被删除掉是根据Kruskal算法确定的。

设T为G的一棵生成树，管段eij的权为Wij，则T的权定义为:

(1)

所有生成树中权重最小的是G的一棵最小生成树，可以采用Kruskal等算法求得，剪枝环状管网生成一棵最小树。

2 Kruskal算法生成树的实现

2.1 Kruskal算法的基本思想

含有n个节点的管网连通图G(V，E，W)和其生成树T的节点V集合相同，定义生成树T(V，E，W)的初态为空集，即生成树只是由n个节点构成而无任何边的n个非连通图T=(V，{φ}，{φ})，因节点之间没有管段，故每个节点自成1个连通分量。先对环状管网图G中的管段进行分析和分类，人工赋予不同的权重。对管网图G中的所有管段进行第1次遍历，若遍历到的管段的权重最小，即为保留管段，则将此管段直接加入到最小生成树T中的E集合。再对权重较大的管段进行第2次遍历，如果管段的2个节点依附于T的2个不同的连通分量，则将此管段加入最小生成树T中的E集合，同时把2个连通分量连接为1个连通分量；若被遍历到的2个节点同属1个连通分量，说明连接此管段后会造成回路，故不连接这2个节点。遍历所有管段后，可使T只有1个连通分量，便构建了1棵连通的生成树，可用于管段流量的初分配。

2.2 Kruskal算法的实现方法

根据环状给水管网图构建带权的邻接矩阵M，邻接矩阵M由4个元素组成，其格式为：

管段编号，管段的起点，终点，管段权值

以图1的环状给水管网为例，其邻接矩阵保存格式及数据如表1所示，管段1、2、3、10和12的权值最小，属保留的管段，其他管段按照Kruskal算法删除连枝以生成树。

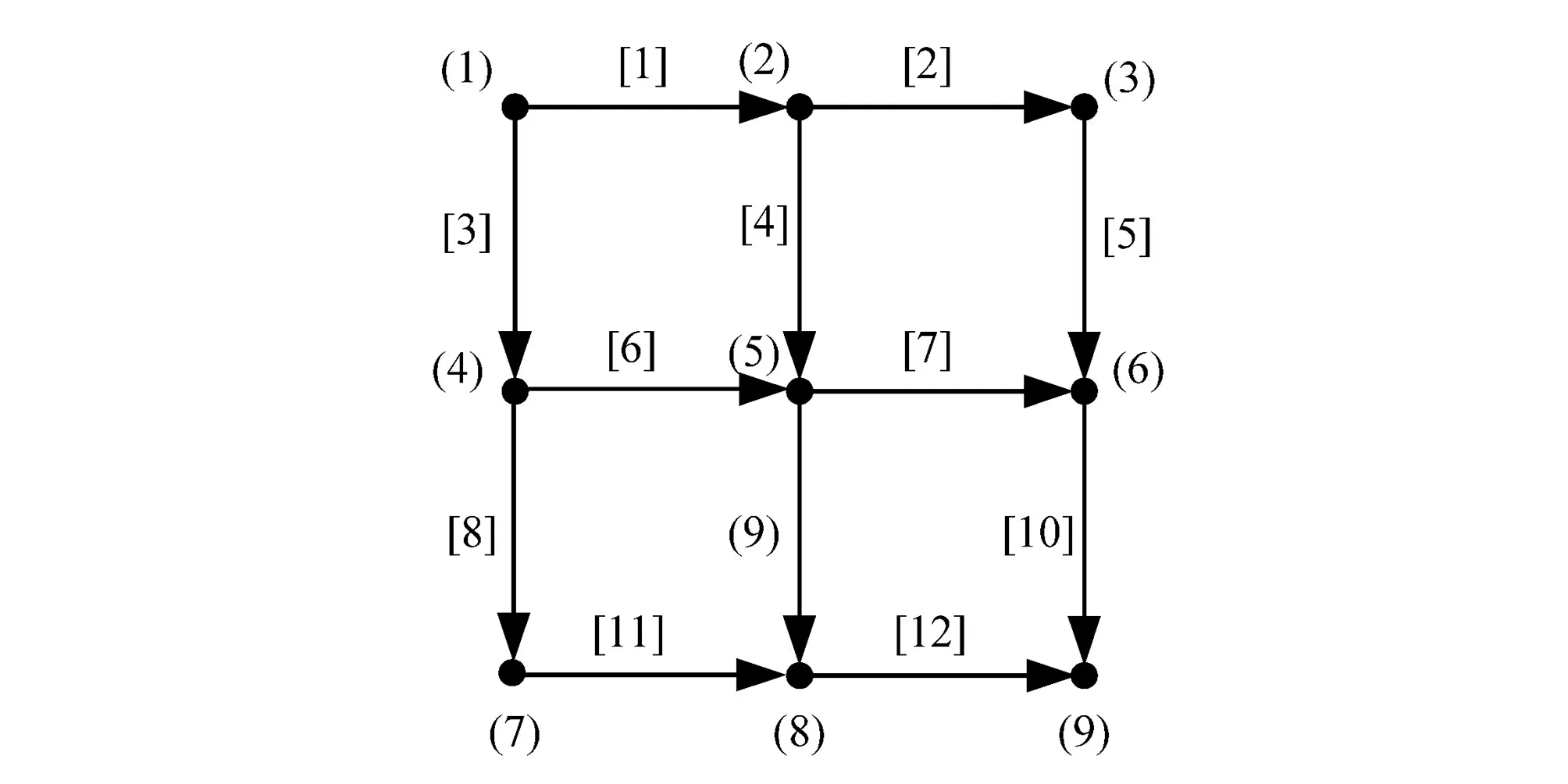
图1 环状给水管网图Fig.1 The looped pipe network of water supply

在使用Kruskal算法对环状连通管网图生成树的实现过程中，根据邻接矩阵的格式，构建一个加权的2维管段数组Looped(Edge, 4)，分别储存每个管段的编号、起点、终点和权值这4个元素，Edge为环状管网的管段编号。还设置一个Root(VertexNum)数组，使用自定义函数Search搜索每个管段的起

表1 邻接矩阵格式及数据Tab.1 Fortmat and data of adjacency matrix

点和终点所属的连通分量，VertexNum为节点编号。Root(VertexNum)数组中每个节点VertexNum的初值为0，表示管网的各个节点在不同的连通分量上，遍历到一条管段后，读取管段的起点(StartVertex)和终点编号(EndVertex)，用Search自定义函数搜索2个节点所在树的根结点，也就是在Root(VertexNum)数组中的序号。若StartVertex和EndVertex的根结点不同，表示所对应的管段不在同一连通分量上，则将这条管段存储在生成树Tree数组中，并把StartVertex的值赋给终点数组Root(EndVertex)，合并2个节点所属的连通分量为1个连通分量。

邻接矩阵的排列顺序影响着生成树过程中连枝的选择，可以对邻接矩阵的权值从小到大进行排序，仅遍历一次便可构建最小生成树。因在环状管网生成树过程中，只有人工干预保留部分管段，所以管段的权值只有1和2，权值为1的管段优先保留下来，权值为2的管段根据生成树的算法再确定是否保留或删除，为此可以对邻接矩阵的权值不进行排序，只是对管段进行2次遍历，第1次遍历只把权值为1的管段直接存储到Tree数组中，然后进行第2遍历，把权值为2的管段根据Kruskal算法存储到Tree数组。

用Kruskal算法实现的过程中，首先把邻接矩阵的元素以文本文件形式保存，程序读取所有管段的编号、起点、终点和权值到Looped(Edge, 4) 数组，然后根据优化搜索算法判断每个管段是否在同一连通分量上，最后得到环状管网图的最小生成树，以数组Tree(Edge, 4)的形式存储并写入交换格式文件中。

对于图1管网图按照表1的邻接矩阵，用Kruskal算法构建最小生成树T，则会完全保留权重为1的管段1、2、3、10和12，删除权重为2的部分管段6、7、9、11。得到的生成树T的管段集合M={1，2，3，10，12，4，5，8}，节点集合V与管网图G相同。若对得到的生成树不是很满意，可修改管段的权重，也可增加管段权重的级数为3级或更多，权值改为1、2和3，把最想删除的管段权重设置为3，再通过程序生成最小树。Kruskal算法的主程序代码如下：

Option Base 1

Sub main()

Dim Root() As Integer

Dim i As Integer, j As Integer, k As Integer

Dim StartVertex As Integer, EndVertex As Integer

Dim VertexNum As Integer, Edge As Integer

Dim Looped() As Integer, Tree() As Integer

Open ActiveDocument.Path & "in.csv" For Input As #1

Input #1, VertexNum, Edge ‘读取管网图的节点总数和管段总数

ReDim Root(VertexNum)

ReDim Looped(Edge, 4)

ReDim Tree(Edge, 4)

For i = 1 To Edge

Input #1, Looped(i, 1), Looped(i, 2), Looped(i, 3), Looped(i, 4)

Next i

Close #1

For i = 1 To VertexNum

Root(i) = 0

Next i

Open ActiveDocument.Path & "out.csv" For Output As #2

Write #2, "管段编号", "起始节点", "终止节点", "管段权重"

For k = 1 To 2

For i = 1 To Edge

StartVertex = Search(Root, Looped(i, 2))

EndVertex = Search(Root, Looped(i, 3))

If (StartVertex = EndVertex) And Looped(i, 4) = 2 Then

Debug.Print Looped(i, 1) '删除的连枝

End If

If (StartVertex <> EndVertex) And Looped(i, 4) = k Then

Root(EndVertex) = StartVertex

For j = 1 To 4

Tree(i, j) = Looped(i, j)

Write #2, Tree(i, j),

Next j

Print #2,

End If

Next i, k

Close #2

End Sub

自定义函数Search的代码：

Function Search(Root() As Integer, VertexNum As Integer) As Integer

Dim i As Integer

i = VertexNum

Do While Root(i) > 0

i = Root(i)

Loop

Search = i

End Function

3 在AutoCAD平台上搜索环状管网生成树的实现及算例研究

3.1 工程条件

某市区供水管网如图2所示。在AutoCAD平台上，假如所有管道的图层为“铸铁管”，可采用遍历技术对管段和节点进行自动编号，形成不带权的3元素邻接矩阵，以.csv交换格式文件形式保存[1,5]。对需保留的管道，手动选择并改变其图层为“Tree”。为表示管道的不同权重，设定“Tree”图层的线宽为0.35 mm，定义在该图层的管道权值为1，设定“铸铁管”图层的线宽为0.2 mm，表示管道权值为2。用Excel修改3元素邻接矩阵，增加每条管道的权重元素，形成带权的4元素关联矩阵，即其矩阵元素仍按表1的格式存储，数据内容见表2。

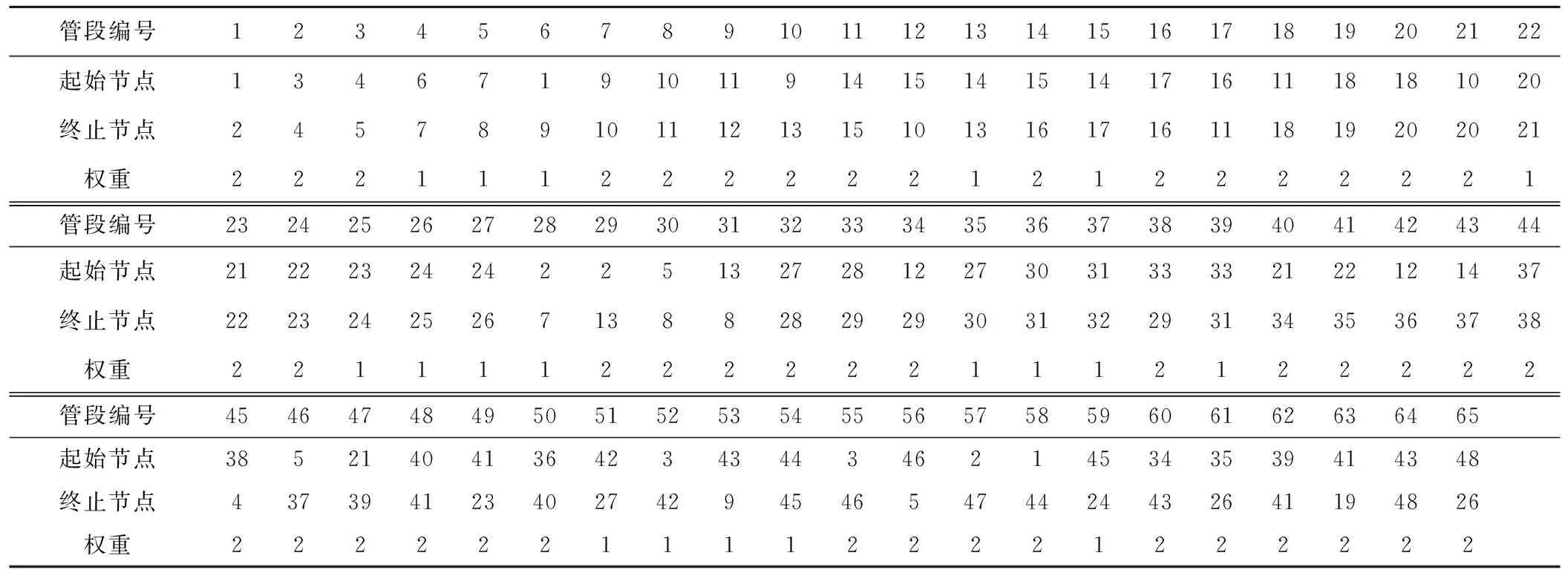
表2 某市区供水管网邻接矩阵Tab.2 The adjacency matrix of water supply pipe network

图2 某市区供水管网现状图Fig.2 The water supply pipe network

3.2 在AutoCAD平台上生成树

首先使用前面的Kruskal算法程序，读取某市区供水管网的邻接矩阵，即表2的数据，判断管段的2个节点的根结点是否相同，若相同则为应删除的连枝。根据欧拉公式，本算例有18个环，所以产生的连枝数也为18，具体删除的管段见表3。

表3 删除的管段Tab.3 The deleted pipe section

然后在AutoCAD平台上遍历搜索环状给水管网的所有管段，用选择集的方法识别管段编号，若遍历的管段为表3中应删除的管段，则修改该管段到“0”图层，也可直接删除，非常直观地实现了把环状管网自动生成树，生成的树状管网如图3所示，程序代码如下：

Sub 删除连枝()

Dim Linea As AcadLine

Dim Obj As AcadEntity '遍历图形对象用

Dim SSetColl As AcadSelectionSets '定义选择集集合

Dim ssetObj As AcadSelectionSet '选择集对象

Dim name As String '选择集名称

Dim Textobj As AcadText '写直线编号用的文字对象

Dim Sp As Variant, Ep As Variant '直线两端点

Dim Cp As Variant '直线中点坐标，要计算

Dim Lp As Variant, Rp As Variant '为形成一个选择框，定义左上角和右下角坐标

Dim TextHeight As Single '定义管段编号的文字高度

ReDim Cp(0 To 2) As Double

ReDim Lp(0 To 2) As Double

ReDim Rp(0 To 2) As Double

Dim gpCode(0) As Integer

Dim dataValue(0) As Variant

Dim groupCode As Variant, dataCode As Variant

gpCode(0) = 0

dataValue(0) = "TEXT"

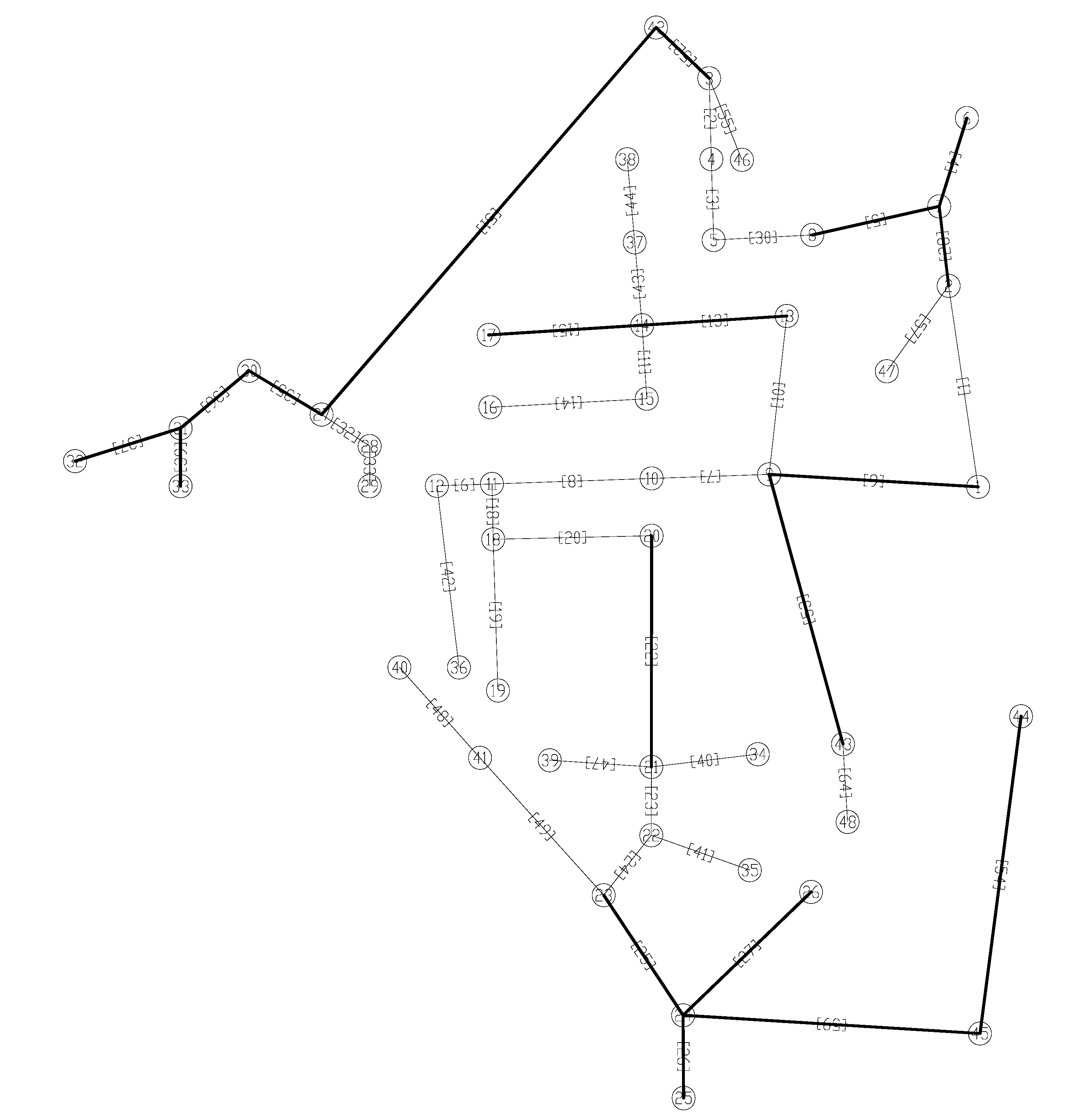
图3 某市区供水管网自动生成树Fig.3 Automatic spanning tree of the water supply pipe network

groupCode = gpCode

dataCode = dataValue

TextHeight = 100 '管段编号和节点编号的文字高度

name = "SSET" '选择集名字

Set SSetColl = ThisDrawing.SelectionSets

On Error Resume Next

For Each Obj In ThisDrawing.ModelSpace

If Obj.ObjectName = "AcDbLine" Then

Set Linea = Obj

Sp = Linea.Startpoint: Ep = Linea.Endpoint

Cp(0) = (Sp(0) + Ep(0)) / 2: Cp(1) = (Sp(1) + Ep(1)) / 2: Cp(2) = (Sp(2) + Ep(2)) / 2 '直线中点，即管段编号插入点

'以下为选择集定义容错处理的代码

If Not IsNull(SSetColl.Item(name)) Then

Set ssetObj = SSetColl.Item(name)

ssetObj.Delete

End If

Set ssetObj = SSetColl.Add(name)

Lp(0) = Cp(0) - TextHeight: Lp(1) = Cp(1) + TextHeight: Lp(2) = Cp(2) '在直线中点形成一个矩形选择框

Rp(0) = Cp(0) + TextHeight: Rp(1) = Cp(1) - TextHeight: Rp(2) = Cp(2)

ssetObj.Select acSelectionSetWindow, Lp, Rp, groupCode, dataCode

If ssetObj.Count = 1 Then

Set Textobj = ssetObj.Item(0)

If InStr("[12][16][17][21][29][31][34][38][45][46][50][56][58][60][61][62][63][65]", Textobj.TextString) Then

Debug.Print Textobj.TextString

Linea.Layer = "0" '修改连枝到“0”图层，也可直接删除

Textobj.Layer = "0"

End If

Else

MsgBox "节点编号错误" '可能没有编号，或者编号字体太大或者矩形选取框太小等原因

Exit For

End If

End If

Next Obj

End Sub

4 结 语

本文根据Kruskal最小生成树算法的基本思想，对环状给水管网的邻接矩阵进行深度优化搜索，筛选出连枝而实现了自动生成树的目的。在AutoCAD平台上遍历所有管段可自动生成带权重的邻接矩阵，根据Kruskal算法筛选出应删除的管段，使环状管网直观地生成树。程序能够根据每个管段的权重，识别人为保留的管段，生成的树得到优化，有助于提高大规模环状管网的设计效率。

在节点流量和连枝流量已知的情况下，满足节点流量平衡的条件，利用Kruskal算法自动生成树，使管段流量初分配很容易实现。

□

参考文献：

[1] 赵星明,王 萱.环状给水管网关联矩阵的建立[J].中国农村水利水电,2012,(11):129-131,135.

[2] 严煦世,刘遂庆.给水排水管网系统[M]. 3版. 北京:中国建筑工业出版社,2014:79-80.

[3] 唐策善,李龙澍,黄刘生.数据结构[M]. 北京：高等教育出版社,2000:123-135.

[4] 卢有杰, 吴炜煜.C语言高级程序设计[M]. 北京:清华大学出版社, 1991:19-86.

[5] 赵星明,王 萱.基于扩展数据的给排水管网拓扑关系的构建[J].山东农业大学学报(自然科学版),2012,43(4):549-554.

[6] 宋 芹,赵星明,艾典胜.输水管道水锤分析与防护技术[J].山东农业大学学报(自然科学版),2017,48(1):84-87.

[7] SeijiKataoka,TakeoYamada.Algorithms for the minimum spanning tree problem with resource allocation[J].Operations Research Perspectives, 2016,(3):5-13.