管片接缝密封垫接触面泄漏率的数值模拟研究

肖明清， 张超勇， 薛光桥， 虞雄兵

(1. 中铁第四勘察设计院集团有限公司， 湖北 武汉 430063； 2. 水下隧道技术国家地方联合工程研究中心， 湖北 武汉 430063； 3. 华中科技大学， 湖北 武汉 430074)

0 引言

盾构法隧道采用管片拼装式衬砌，接缝采用密封垫防水，密封垫常用材料为三元乙丙橡胶(EPDM)和遇水膨胀橡胶，或者由二者复合的橡胶材料。国内外许多学者做了密封垫防水性能以及耐水压力的研究。文献[1]对密封条进行了防水试验，发现管片接触面与密封条间有泄漏的可能。文献[2]针对影响密封垫防水能力的闭口及载荷形式等因素进行了一系列密封垫防水试验，并做了系统的研究。文献[3]认为弹性密封垫的防水能力与其孔洞率和断面形式有关,其中断面形式对防水能力的影响较为显著。文献[4-5]采用数值模拟的方法，对接缝张开及错开工况下密封垫失效机制进行了分析。文献[6-8]采用自主设计的新型弹性密封垫耐水压测试装置，进行了一字缝、T型缝的防水试验。文献[9]采用数值模拟的方法，对压缩情况下密封垫孔洞的合理变形、薄弱处应力集中、最大张开量下接触应力的大小及其分布等多因素进行综合分析。文献[10]从防水机制出发，结合管片拼装的需要，以有限元为工具分析并提出了密封垫断面的主要设计参数。文献[11-12]进行了考虑水压、气压作用下的数值模拟，研究了密封垫在这些情况下的防水机制。文献[13]提出由于密封垫接触面凹凸不平，存在极细微渗漏孔洞，防水能力受接触面最大接触应力和接触面细微孔洞的水流阻力双控制，通过提高密封垫接触面的平整度进而减少细微孔洞的数量与大小，是加强防水能力的关键因素。

从上述研究可以看出，目前的研究主要是使用数值模拟和试验2种手段，防水性能通常考虑密封垫接触应力、压缩力、接缝张开量与错台量、防水数值等指标，但从微观角度对密封垫的防水性能研究较少。此外，笔者在一些穿越含沼气地层的工程案例中发现，尽管管片接缝不漏水，但存在漏气现象，也需要从微观角度进一步研究防水防气机制。本文在前人研究的基础上，从弹性密封垫表面微观形貌着手研究，基于Roth模型建立盾构管片间密封垫在压缩状态下的微观泄露通道模型，推导密封垫间流体的泄露率公式；借助ANSYS有限元工具对不同工况下的密封垫模型进行数值模拟，建立微观下密封垫表面的粗糙峰有限元模型，研究粗糙度的变化对密封性能和泄露率的影响；最后，对不同影响因子进行灰色关联度分析，得到影响密封垫密封性能的主次因子排序，以期为改善盾构隧道密封垫防水性能提供技术支撑。

1 密封垫间泄露通道建模

1.1 微观接触模型分析

粗糙度指加工表面上具有的较小间距峰谷所组成的微观几何形状特性，一般可用轮廓算术平均偏差Ra表示，单位为μm。从微观上看，密封垫的表面是由众多服从Gauss分布的随机波峰或波谷组成，波峰也称为粗糙峰。粗糙峰具有充分的随机性，其形貌受包括粗糙度在内的一些参数的影响，用Fourier变换及其逆变换在计算机上生成随机粗糙表面如图1所示。

(a) 粗糙度Ra=0.5 μm

(b) 粗糙度Ra=1 μm

(c) 粗糙度Ra=1.5 μm

由图1可知，粗糙峰会随着粗糙度的增大而变得陡峭。密封垫的防水机制从根本上说，是密封垫相互挤压，其表面微观波峰或波谷相互接触、挤压和填充，缩小密封间隙，进而达到防水的目的。

密封垫的粗糙表面接触常用的接触模型有圆柱-平面接触、圆锥-平面接触和球体-平面接触。本文通过表面轮廓仪的观察，选用更符合实际情况的圆锥-平面接触模型，如图2所示。随机粗糙表面模型过于复杂，不便于计算和分析。Roth模型是用连续相同的等腰三角形去简化随机粗糙峰，该模型结构简单，能直观地反映微观表面的接触情况，便于计算和分析流体在接触面间的泄漏情况。两密封垫相互接触的Roth模型如图3所示。

图2 圆锥-平面接触模型

图3 两密封垫相互接触的Roth模型

1.2 泄露率公式推导

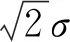
图4 光滑的刚性表面和粗糙度为的弹性表面相接触的Roth模型

假设密封垫间液体为均匀牛顿流体，根据雷诺数可判断其流动状态为层流，液体流动的Navier-Stoks(纳维-斯托克斯)方程为：

(1)

式中：ρ为流体密度；u,v,w为流体在t时刻、点(x,y,z)处的速度分量；p为压力；f为单位体积流体所受外力；μ为黏性系数。

(2)

将边界条件y=0,u=0和y=h,u=0代入，可得速度分布函数

(3)

对单个泄漏通道积分，可得其体积泄露率

(4)

式中：h为峰高； Δp为密封界面内外两侧压差；B为密封宽度。

(5)

1.3 泄露率参数计算

表1 不同粗糙度下锥形峰初始参数

图5 微观接触模型

2 密封垫数值模型建立

2.1 数值模型

本文采用的密封垫尺寸及沟槽尺寸如图6所示，其在有限元软件上建立模型如图7所示。由于混凝土管片的刚度远大于弹性密封垫，所以可以将沟槽设置为刚体，密封垫则选用超弹性材料。由于2D模型不适用于显式动力学，3D模型又过于占用计算资源，所以建立2.5D模型，即用1层网格覆盖所有实体；下沟槽设置固定约束，沟槽与密封垫间设置面接触，并采用罚函数减少穿透，密封垫间设置自接触；限制全部实体在非x、y方向上的自由度，并对上沟槽的所有面施加位移约束以完成密封垫的压缩过程。

(a) 橡胶密封垫断面图

(b) 沟槽示意图

图7 弹性密封垫和沟槽有限元模型

三元乙丙橡胶材料是超弹性体，具有材料、几何和接触上的非线性。表征橡胶材料本构关系的模型较多，本文采用的模型是应用较多的Mooney-Rivlin参数模型[15]，其满足的应变势能函数关系为：

W=C10(I1-3)+C01(I2-3)。

(6)

式中：W为应变能函数；I1、I2为应变张量不变量；C10、C01为模型中的2个重要参数，其数值由拉缩试验数据拟合得到。

橡胶材料的弹性模量E与橡胶硬度(邵氏硬度)Ha以及参数C10、C01满足如下关系：

E=6(C10+C01)=(15.75+2.15Ha)/(100-Ha)。

(7)

C10=4C01。

(8)

本文选取4组不同硬度的橡胶材料，其Mooney-Rivlin模型参数值如表2所示。

表2 4组不同硬度的橡胶材料的Mooney-Rivlin模型参数值

2.2 模型验证

为了验证材料参数选取、接触设置、网格划分等步骤是否合理，对本文建立的密封垫沟槽接触模型和微观锥型峰接触模型进行对比验证。文献[16]使用ANSYS有限元软件对密封垫进行了压缩模拟，在张开量为6 mm工况下提取出其表面应力分布，本文在同样张开量下得出的数值模拟结果与文献[16]对比如图8所示。

图8 数值模拟计算结果对比

可以看到，本文模型计算结果与文献[16]计算结果有着很高的相似性，大体趋势相同，但由于密封垫表面宽度不同，波峰略有延迟，另外局部上数值略有差距。造成差距的原因主要是密封垫的大小以及横截面形貌上的差异，但是差距并不大，平均误差都能保持在15%以内。通过以上对比，验证了模型的准确性和合理性，为下一步各因素对防水性能的敏感性分析奠定了基础。

3 数值模拟结果与分析

3.1 不同参数下微观泄露率分析

3.1.1 粗糙度对泄露率的影响

从微观角度看，不同粗糙度的密封垫表面锥型峰具有不同的初始高度和锥角，进而泄漏通道尺寸和泄漏率不同。在上述沟槽密封垫数值模型中，将硬度67 HA(邵氏硬度)对应的参数赋给橡胶密封垫，并设置0 mm错台量、8 mm张开量，压缩完成后在密封垫一侧施加2 MPa均布载荷以模拟水压作用，加载完成后得出接触面上的平均正压力为1.34 MPa。用不同粗糙度对应的参数建立微观锥型峰数值模型，将此正压力加载在圆锥的顶面，结果如图9所示。

(a) 粗糙度Ra = 0.2 μm

(b) 粗糙度Ra = 0.4 μm

(c) 粗糙度Ra = 0.8 μm

从图9可以看出，当粗糙度较小时，在密封垫压缩和水压作用下锥型峰的高度明显降低，泄露通道尺寸更小，有效地抑制了泄露发生。因此，在一定的外界水压作用下，较小的表面粗糙度有可能提升密封性能。假设密封长度为1 m，由公式计算出不同粗糙度对应的泄露率如表3和图10所示。

表3 不同粗糙度对应的泄露率

图10 泄露率与不同粗糙度的关系

由图10可知，随着粗糙度的增大，泄露率逐渐增大，尤其是当粗糙度大于0.8 μm时，泄露率几乎呈指数型增长。因此，控制密封垫表面的粗糙度对密封性能至关重要，但降低粗糙度意味着增加成本，所以建议粗糙度控制在0.4～0.8 μm。

3.1.2 正压力对泄露率的影响

既有研究表明，密封垫表面的正压力会直接影响其防水能力，正压力越大，微观上锥型峰会被压缩得越低，泄露通道尺寸缩小，进而泄露率减小。对粗糙度为0.8 μm对应的锥峰模型进行数值模拟研究，在橡胶材料邵氏硬度设置为67 HA时用不同正压力进行加载，计算出泄露率如表4和图11所示。

表4 橡胶材料邵氏硬度设置为67 HA时的泄露率

图11 泄露率与正压力关系

由图11可以看出，泄露率随正压力增大呈负指数下降，且当正压力超过2 MPa时，正压力继续增长对泄露率减小的效果并不显著。因此，不能一味地增加正压力来提升密封垫防水能力，并且考虑过大的压力对混凝土管片的潜在威胁，正压力不能过大。

3.2 防水性能各影响因素灰色关联度分析

各影响因素对密封垫防水性能均有影响，但影响程度不明确，为此本节采用灰色关联度对各影响因子进行分析，以评价其相关影响程度。

3.2.1 防水性能各因素正交试验

正交试验是研究多因素多水平的一种设计方法，为分析包括粗糙度、橡胶硬度、张开量、错位量等因素对密封垫防水性能的影响规律，以泄露率为主要评价指标、平均正压力为辅助评价指标，对上述因素设计4因素4水平的正交试验。试验共16组工况，试验结果如表5所示。

3.2.2 各因素相对关联度计算与分析

在灰色关联分析中，首先确定评价单元序列。设有m个评价指标、n个样品，本文单元序列分别为粗糙度、张开量、硬度和错位量，目标序列为平均正压力和泄露率。在多指标评价中，因各指标单位、量级不同，无法进行直接评价，故需对原始数据进行无量纲化处理，即用原始数据除以该组数据的算术平均值，得到初始数据xik、yik，再由相关度公式计算其相关度：

ξi(k)=

(9)

式中:ξi(k)为xi对y(k)在k点的关联系数；|y(k)-xi(k)|为第k点y与xi的绝对差；minimink|y(k)-xi(k)|为y数列与xi数列在k点的二级最小差绝对值； maximaxk|y(k)-xi(k)|为y数列与xi数列在k点的二级最大差绝对值；ρ为灰色分辨系数，取值范围0～1，一般取0.5。

将各因素关联系数代入式(9)，可求出xi与y(k)的关联度，再由式(10)即可计算评价因素对目标序列的关联度：

(10)

由此可得出各因素之间的关联度如表6所示。

表5 4因素4水平正交试验

表6 各因素之间的关联度

由表6可以得出,影响平均正压力的主次因素顺序为： 硬度、张开量、错位量、粗糙度。其中，硬度和张开量的影响明显，错位量的影响较小，粗糙度不参与对平均正压力的影响。而且，通过同一因素组内的均值比较可知，硬度越大，平均正压力越大，这与以往的认知基本一致；错位量对平均正压力的影响并不是线性的，而是高低起伏的，但显而易见的是，0 mm错位工况下平均正压力最大，所以在实际工程中，控制错位量对防水也至关重要。

影响泄漏率的主次因素顺序为： 粗糙度、硬度、张开量、错位量。其中，粗糙度的影响尤其显著，因为粗糙度直接决定了微观锥形峰的初始高度。由于泄漏率公式中没有与张开量和硬度直接相关的参数，所以这2个因素的影响稍弱。错位量对泄漏率的影响排在第4位，但显然错位量越大，泄漏率也会随之增大。一方面是因为错位量影响了正压力，进而间接影响锥形峰高度；另一方面，错位量增大会造成密封宽度减小，由泄漏率公式可知泄漏率增大。外界水压是正交试验中未包含的因素，但外界水压作用于密封垫一侧，一方面，通过挤压密封垫，增加密封垫接触应力进而缩小泄漏通道高度；另一方面，作为泄漏率公式中的参数正比例影响泄露率。

4 结论与讨论

本文基于Roth模型建立了密封垫接触面的泄漏通道模型，推导出了泄露率的计算公式，通过建立宏观密封垫数值模型和微观锥型峰数值模型，完成了以粗糙度、张开量、错位量和硬度在内的4因素、以泄露率和平均正压力为评价指标的正交试验，得出结论如下：

1)本文基于Roth模型建立了密封垫接触面的泄漏通道模型，推导出了泄露率计算公式，泄露率可以作为评价密封垫防水性能的一个重要指标。

2)随着粗糙度的增加，泄露率逐渐增大，尤其是当粗糙度大于0.8 μm时，泄露率几乎呈指数型增长。所以控制密封垫表面的粗糙度对密封性能至关重要，但降低粗糙度会增加工程造价，建议粗糙度控制在0.4～0.8 μm。

3)在粗糙度、硬度、张开量、错位量几个因素中，粗糙度对于泄露率的影响最为显著，因为粗糙度直接决定了初始泄漏通道的尺寸，所以控制粗糙度的数值显得尤为重要；同时，研究降低密封垫表面粗糙度的方法，对提升防水能力和防气能力具有重要意义。

微观泄露通道模型较多，具体采用哪一种模型更为合适，有待今后进一步研究；此外，通过降低密封垫表面粗糙度的方法可以提升防水防气能力，但具体方法有待进一步研究。