基于Matlab的液压系统可靠性仿真研究∗

胡立明 李建华 王 涛

（中国人民解放军陆军炮兵防空兵学院 合肥 230031）

1 引言

液压系统模型的动态仿真最接近于实际的液压系统，其可靠性和准确性直接决定着控制器的优劣性，并且对液压系统的设计、制作以及优化都会产生很大的影响，因此增强其可靠性具有重要的理论意义和现实意义［1］。随着液压系统的发展和对被执行对象和控制算法精度要求的不断精细，常规的微分方程或者差分方程建立的简单模型显然已满足不了当前对控制和仿真的需要［2］。

针对此问题，本文对其整个液压系统结构进行了分析和动态建模，在建立的动态模型基础上，分别以设定的普通PID控制和模糊PID控制策略对液压系统进行控制，在Simulink中建立液压系统仿真模型，通过修改动态参数对其液压系统进行仿真。仿真结果表明：本文设计的模糊PID控制策略能够较精确地反映出动态响应特性和稳态特性，从而验证了所设计的模糊控制策略的正确性和可行性，并为液压系统的控制研究提供基本的理论依据。

2 液压系统动态建模

一个完整的液压系统由液压泵、液压阀、液压缸、箱体等组成，如图1所示。对于常见的开关型阀控缸系统，泵出的油经开关阀进入液压缸，并通过开关阀控制液压缸进油，从而实现活塞运动［3］。

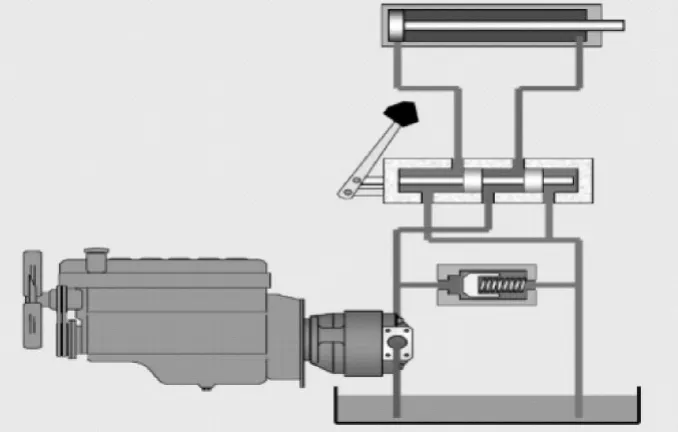
图1 液压系统的模型

以伺服阀为研究对象，得

式中，QL为负载流量（m3/s）；kq为流量增益（m2/s）；Q为阀的负载流量（m3/s）。

建立阀芯位移与电流之间的关系，得

式中，阀芯的行程范围对应电流为4mA～20mA，对中位置电流为12mA。

阀的负载流量则与阀的锐边流口的压降平方根成正比［4］，得

式中，QN为阀的额定流量（m3/s）；ΔpN为阀的额定压降（Pa）；Δp为阀的实际压降（Pa）。

依流体连续体方程得

式中，A为活塞有效面积（m2）；y为活塞位移（m）；V为总体积（m3）；β为弹性模数（N/m2）。

根据牛顿第二定律可得

式中，Fg为液压缸驱动力（N）；B为粘性阻尼系数（N·s/m）；F是作用在活塞上的任意外力（N）。

对应式（1）、（4）、（5）进行拉式变换得

液压系统中具体的各项参数如表1所示。

表1 液压系统参数

3 仿真模型

根据式（6）、式（7）、式（8）所示的方程可得到方框图，根据框图得到用于Simulink仿真模型［5］。输入端为伺服阀的电流值，输出端为含有一定系数的驱动力，k=1/100。

1）普通PID闭环模式如图2所示。通过大量实验［6］，整定三个 PID 参数，kp=0.001，ki=0.001，kd=0.01。

图2 普通PID闭环模式

2）模糊PID控制闭环模式如图3所示。

图3 模糊PID闭环模式

4 液压系统控制算法研究

液压系统的主要用途是控制伺服阀，通过对液压系统期望流量的实时控制，进而实现液压系统的控制［7］。下面对某液压系统就普通PID和模糊PID控制分别设计相应的控制器，并确定控制器的三个参数。

4.1 普通PID控制

普通PID控制系统原理框图如图4所示。

图4 普通PID控制系统原理图

其中，et是控制器的输入量；yt为实际的输出量；xt为系统输入量；ut为被控对象的输入量。

偏差可表示为

普通PID控制器的控制规律的理想数学表达式为［8］

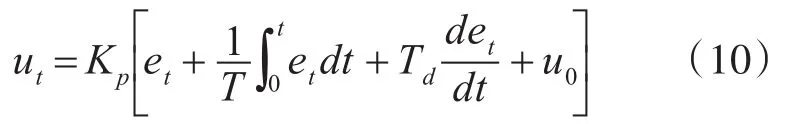
式中，u0为控制常量；Kp为放大系数；Td为微分常数；Ti为积分常数。

于是可以得出系统输出为

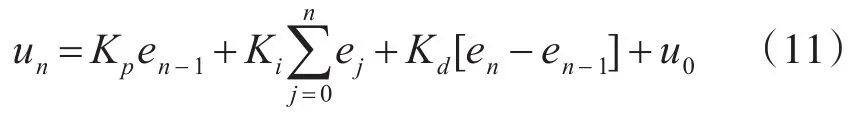
根据递推关系，得到

控制器的增量表达式：

设预期阀门流量为Qn，反馈的含有系数的驱动力为Fdn，则产生的偏差量为［9］

控制信号为

4.2 模糊PID控制

4.2.1 模糊控制结构及原理

模糊控制基本工作原理如图5所示，其主要功能是通过模糊逻辑语言实现对复杂系统中非线性信息的有效处理［10］。

图5 模糊PID控制基本工作原理

4.2.2 模糊控制器设计

1）模糊PID控制器

模糊控制器是根据模糊规则表，预定义的参数论域和模糊子集，隶属度函数和参数控制模型，得到相应的控制参数。

2）确定控制器结构

根据控制对象，选择单变量二维控制器结构，所有变量的模糊子集均选择为｛NB，NM，NS，Z，PS，PM，PB｝，控制系统的误差e及其变化率ec均选择较大的论域，分别为［-32，32］，［-8，8］，经参考实验经验，PID控制器的参数kp论域为［-0.012，0.012］，ki论域为［-0.0012，0.0012］。系统误差e和误差变化率ec，比例系数kp，积分系数ki，微分系数kd变化范围定义为模糊集上的论域［11］。其模糊子集为 e，ec，kp，ki，kd=｛NB，NM，NS，Z，PS，PM，PB｝，子集中元素分別代表负大，负中，负小，零，正小，正中，正大。

3）确定模糊变量隶属度函数

经上一步中各参数的模糊子集以及论域确定后，需要确定各参数的隶属度函数，选用较高灵敏度的三角形隶属函数，S形隶属函数和Z形隶属函数，隶属度函数曲线如图6所示。

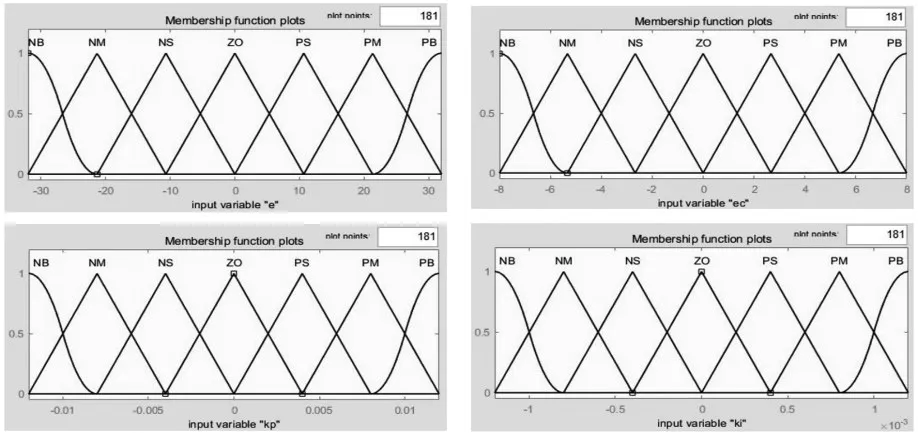
图6 e、ec、kp、ki隶属度函数曲线

4）确定模糊控制规则

控制规则是模糊控制器进行校正的主要依据，通常根据工作经验确定［12］。具体的模糊控制规则表如表2、表3、表4所示。

表2 kp的模糊规则表

表3 ki的模糊规则表

表4 kd模糊规则表

5）模糊推理及反模糊化

本文采用常用的Mamdani型模糊推理方法，利用重力中心法进行反模糊化，对应的重力中心法公式为

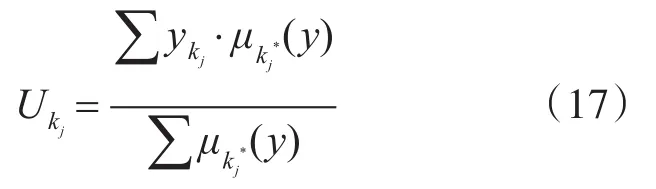
5 仿真结果与分析

对液压系统进行动态仿真，将普通PID控制与模糊PID控制进行比较［13］。从图中可以清晰地看出模糊PID控制液压系统在阶跃输入下，系统响应明显变快，在0.1s之前，出现剧烈振荡；在0.2s时就已经达到稳定状态。

1）若输入电流值为20，则反馈的含有系数的驱动力值为32。模糊PID控制的kp，ki，kd参数图曲线如7所示。

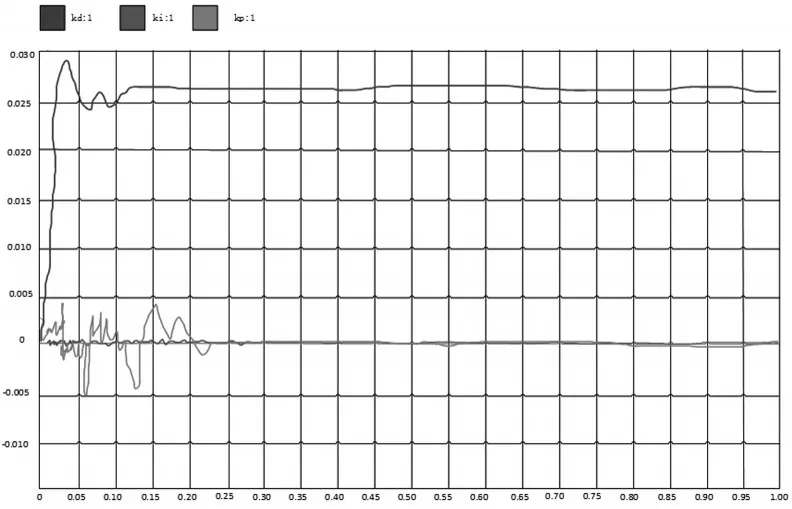
图7 kp、ki、kd参数曲线

得到对应的响应曲线如图8所示。从图8中分析得知，模糊PID控制的阶跃响应曲线，系统的动态性能指标：延迟时间为0.009s，上升时间为0.008s，最大超调量为21.25%，调节时间为0.066s；普通PID控制的阶跃响应曲线，系统的动态性能指标：延迟时间Tdelay=0.01s；上升时间Tstep=0.027s；最大超调量σ=0%；调节时间为0s。

2）若输入电流值为12，则输出的含有系数的驱动力值为32。模糊PID控制的kp，ki，kd参数图曲线如9所示。

图9 kp，ki，kd参数曲线

得到对应的响应曲线如图10所示。模糊PID控制的阶跃响应曲线，从图10中分析得知，系统的动态性能指标：延迟时间为0.009s，上升时间为0.008s，最大超调量为25.3125%，调节时间为0.09s；普通PID控制系统的动态性能指标：延迟时间为0.013s，上升时间为0.025s，最大超调量为0%，调节时间为0s。

图10 普通/模糊PID控制的阶跃响应曲线

3）普通PID控制的阶跃响应曲线，系统的动态性能指标，保持参数Ki=0.001，Kd=0.01不变；改变比例度Kp参数，分别为 0.001，0.01，0.1，选取优化参数，如图11所示。三条曲线都在0.2s内达到稳定状态，含有系数的驱动力分别为32，31.7，29.1。系统中设置的负载力为3200，因含有系数的驱动力与负载力二力平衡，所以优先选择Kp1=0.001。

图11 不同的比例度Kp参数

6 结语

通过动态仿真结果可知，液压控制系统的主要动态性能指标在所要求的精度范围之内，响应曲线能达到预期的要求［14］。

1）在电流输入值相同情况下，普通PID控制与模糊PID控制效果对比，突出了模糊PID控制的冲击响应迅速，反应时间较短、延迟时间较短和一定量的大超调量。

2）改变普通PID控制的Kp参数，其他参数不变，自身对比，得到优化的Kp参数。这样使得普通PID的参数更合理地与模糊PID参数对比。

3）模糊PID控制器通过三个参数模糊化，使控制器的控制效果更加合理。