基于分布式演化算法的编队对空防御任务分配方法∗

周 晶 林 众 卢一鸣 何应强

（海军大连舰艇学院作战软件与仿真研究所 大连 116018）

1 引言

对空防御作战是海上编队的重要作战样式，其典型特征是战斗节奏快，影响决策因素多，反应时间短［1～2］。任务分配问题是编队对空防御中核心问题之一，在有限的时间内完成科学有效任务分配问题是编队进行对空防御的关键［3］。任务分配问题中要考虑敌方威胁程度、完成任务收益、任务执行时间和资源消耗等多种因素制约，因此编队对空防御中的任务分配问题是一个典型的多目标优化问题（Multi-Objective Optimization Problem，MOOP）。多目标优化问题求解已被证明是NPH问题，当任务规模增加时，求解难度呈几何增长。除了优化目标多，任务分配问题还需要考虑涉及时间、空间、兵力能力和执行顺序等大量的约束条件。目前已有一些算法用于多目标任务分配。早期最常见的方法是采用集中式方式进行求解，完成求解后将分配方案指派给各执行兵力［4］，但这类方法存在单点失效问题和容错性较差等问题，且无法解决大规模问题。近年来，分布式多任务分配方法被提出，大致可分为以下几类：分布式完全搜索算法、分布式局部搜索算法、基于拍卖机制的算法和分布式蚁群算法等［5～7］。分布式完全搜索算法能确保解最优，但各节点间需要较大的通信和计算成本，在单节点计算或通信资源有限的情况下难以适用；分布式局部搜索算法则大量减少了通信和计算的代价，各个节点在本地搜索最适合自己的任务分配方案，然后通过通信来实现全局任务分配的统一和协同，但这类方法通常难以保证解的质量，求解的效果依赖于具体的应用场景；分布式蚁群算法则将节点视为蚂蚁，模拟蚂蚁觅食的群体行为，来求解最优的任务分配方案。这类方法利用智能启发式优化策略具有资源消耗小的优势，但分布式蚁群算法难以处理大量约束条件的问题，且容易陷入局部最优。

演化算法是应用最广泛的智能优化算法之一，具有与蚁群算法相当的优化能力［8］。近年来，分布式演化算法得到了广泛的应用［9］，但基于分布式演化算法用于多目标任务分配、且在大量约束条件的研究较少。针对以上问题，本文提出一种基于NS⁃GA3的分布式多目标演化算法（以下简称为D-NS⁃GA3算法），将编队对空防御中的约束条件转换为优化目标，与原有的目标函数一起协同优化，通过种群演化收敛得到满足约束条件的全局最优解。

2 任务分配问题分析与建模

为便于后续的演化算法实现，首先给出编队任务分配问题的形式化描述，以下分别定义编队中任务分配的各要素。

1）任务：为实现编队总体作战任务，通常需要对任务进行分解，直到分解为可以单个兵力独立完成的原子任务为止，表示为V=｛v1…vn｝，其中，n为任务的数目。在实际应用场景中，每个任务具有时间限制，假定每个任务在时间上限定了最早可执行的时间和最晚可开始执行的时间，则定义任务的可开始执行时间范围TV=｛［low1，up1］…［lown，upn］｝，其中lowi为任务vi最早可执行的时间，upi为任务vi最晚可开始执行的时间，当时间超过最晚时间时，任务将失效。［lowi，upi］为任务vi可开始执行的时间范围。执行任务所需花费的时间表示为W=｛w1…wn｝，其中wi为执行任务vi所需花费的时间。任务的位置信息是任务分配中需重点考虑的隐私，因此定义当前位置为LV=｛lv1…lvn｝，其中lvi（i=1…n）表示任务vi的当前位置。

2）抗击兵力：表示为A=｛a1…am｝，其中m为兵力的数目。兵力的位置信息为LA=｛la1…lam｝，其中lai（i=1…m）表示兵力ai的当前经纬度信息。

3）分配关系：用于表述作战兵力与原子任务之间的分配关系，P={π1…πn}，其中设定πi为任务vi的分配，当πi=vi→aj表示任务vi分配给兵力ai执行，πj=vj→∅表示任务vj未被有效分配给任一兵力。为便于后续描述，将πi=vi→ai和πj=vj→∅分别简化为πi=ai和πj=∅。为了简化问题模型，假设一个兵力在一个时间点只能完成一个任务，一个任务仅需要一个兵力执行并完成，即不存在需要多个兵协同合作执行才能完成的任务元，且时间是离散化的，以秒为单位。

4）执行序列：Q=｛q1…qm｝，其中qi=｛qi1…qik｝为节点ai所需要执行的k（不同节点的k值可能不同）个任务序列，例如qi=｛v1，v3，v5｝，表示任务v1，v3，v5分配给了节点ai，且节点ai按次序执行这三个任务。

3 基于D-NSGA3算法的多目标任务分配方法

3.1 NSGA3演化算法

NSGA3算法是由Deb等人于2013年提出的，NSGA3算法是在NSGA-2算法的基础上改进而来，主要提升了NSGA-2算法以解决高维优化问题（即当目标数目大于3）时的优化能力［10～11］。其最大的差别点在于选择操作，NSGA2算法采用基于参考点的选择操作代替NSGA2算法中拥挤距离的选择操作来保持非支配解的多样性。主要包括以下四点：确定超平面上的参考点、规范化目标函数、关联操作和小生境保持操作。NSGA3的算法框架如表1所示。

表1 NSGA3算法

3.2 基于Master-Slave模型的D-NSGA3算法

在水面舰艇编队中，编队指挥所作为Master节点来负责NSGA-III的种群初始化、演化迭代、杂交、变异和选择操作等。由于环境随时可能发生变化，进而导致任务相关的指标和信息（如执行任务所需的能耗和完成任务的收益等）发生变化，最终导致评估任务分配策略的好坏也会发生变化。另一方面，由通信速度和覆盖范围受限，单个舰艇往往只能感知到其周围的环境信息，因此，它只负责评估任务分配策略中涉及这些信息的部分。因此，本文将一条舰或担负区域防控的多个舰艇作为一个Slave节点。Master节点会根据每个Slave节点的评估能力对任务分配方案进行分割与分发，Slave节点将接收到的基因片段进行评估，将评估结果返回给Master节点。

文中提出的算法流程如下：1）Master节点首先随机初始化生成大小为N的初始种群作为父代；2）Master节点依据每个Slave节点所掌握的信息对种群个体基因进行分割划分，并将基因片段发送给对应的Slave节点；3）Slave节点接收到Master节点发送的基因片段后进行评估，并将评估函数的计算结果返回给Master节点；4）Master节点收集所有Slave节点返回的评估结果后，计算个体的整体评估值；5）Master节点通过杂交、变异算子产生子代种群；6）Master节点和Slave节点再对子代个体进行评估；7）Master节点对父代种群和子代种群进行非支配排序形成H个非支配层F1…FH；8）Master节点找出前h个非支配层的个体；9）Master节点通过选择操作决定下一代种群，若，则直接选出前h层的个体作为下一代种群，否则通过参考点方法从临界层Fh中选择与F1…Fh-1层的个体一起作为下一代种群；迭代以上5）～9）步直至种群收敛或超过最大迭代次数。

3.3 染色体编码、初始化、杂交、变异及评估

染色体的编码、杂交和变异策略是演化算法中的核心问题，直接影响种群进化的速度和多样性和求解的质量。染色体编码策略如下：每个染色体表述为x=x1…xm，其中xi表示兵力ai可执行的任务的工作序列。此外，针对ai的功能约束，表示ai将按照xi指定的顺序依次考虑执行任务，倘若任务执行后，ai无法在约束条件下执行当前任务时，则ai将跳过该任务继续执行下一个任务。对于染色体x，如果ai按照xi能在满足约束条件的情况下执行任务vj，那么后续的兵力ai+1…am将不再考虑执行vj任务。假定存在2兵力和5个任务，由于存在功能约束，兵力a1可执行任务v1、v2、v3，兵力 a2可执行任务v3、v4、v5，那么，染色体 x=3 1 2 4 3 5 表示兵力 a1将按照顺序考虑执行任务v3、v1、v2，a2将按照顺序考虑执行任务 v4、v3、v5，若 a1执行完 v3和 v1后无法在资源约束或时间约束内成功执行任务v2，那么最终a1可成功执行2个任务；而由于v3已经分配给a1执行，a2仅需按顺序考虑执行v4和v5。该编码方式的优点是所有个体编码长度固定，无需在评估个体时考虑功能约束，简化了评估过程，且易于对个体进行初始化、交叉、变异等操作。

初始化种群采用随机方式，然后根据编码方式，Master节点依据每个兵力ai的功能约束得到它们可执行的任务集合，然后生成的随机排列，作为初始化个体x的第i部分。杂交方式采用经典的单点杂交算子，对于两个父代个体x=x1…xm和y=y1…ym，Master节点随机生成一个1～m间的数k，交换x和y的前k个序列得到子代个体和。在变异算子中采用参数mutPr来控制个体变异的概率。依据概率选出个体的第i个序列xi做变异，Master节点将生成一个的随机排列替换原有的xi。

4 实验结果及分析

为了验证算法有效性和执行效率，将文中的算法与全局搜索算法进行比较，通过设置相同的初试数据和环境变更信息的条件下，两种算法进行对比实验。实验采用基于Tsung-Che Chian的NSGA-III的版本进行二次开发［10］，默认设置演变迭代次数设为200次，杂交概率为1.0，突变率设为0.2。实验环境为：操作系统为Windows 7 64位Professional，CPU i7 7600主频2.80GHz，内存8G，编程环境为Visual Studio2010。

选择4组参数分别为：1）m=5，n=5；2）m=5，n=10；3）m=5，n=20；4）m=10，n=20。当（m=5，n=20）与（m=10，n=20）时，采用完全搜索策略的算法在1 h未能完成计算，而文中提供的算法在5 min内完成求解。通过不同的阈值进行过滤显示，结果如表格2～3所示。

表2 对比试验结果当m=5，n=10

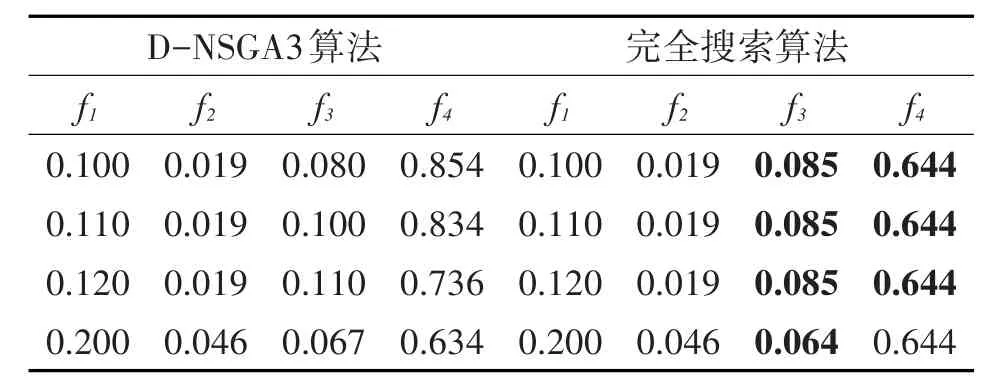
表3 对比试验结果当m=10，n=10

通过比较本文算法和完全搜索策略下的计算结果，发现本文提供的算法可以搜索到接近全局搜索策略下最优解。当m=5且n=5时，两者搜索到的最优解相差仅为0.008；当m=5且n=10时，平均差值为0.0408，而最大的偏差量也仅为0.231，最小偏差值为0；当m=10且n=10时，平均差值为0.14，而最大的偏差量也仅为0.225，最小偏差值为0.003。尽管全局搜索策略可获得最优解，但求解时间较长，只能限于在较小的问题规模下使用。而本文算法在m≥100，n≥800时，仍可以有效寻求最优解，因此该算法具有较好的实用性和推广性。

5 结语

本文针对水面舰艇任务分配问题中优化目标多、约束条件苛刻的问题，提出了一种基于分布式演化算法的多目标任务分配方法，实验结果表明：相比于分布式局部搜索算法，本文的算法能在消耗更少的时间和通信代价下得到接近全局最优的任务分配方案。