基于兰彻斯特方程的兵力编组模型∗
单恒 葛培 朱闽
(陆军炮兵防空兵学院 合肥 230031)
1 引言
兵力编组是指挥员进行战斗部署的主要内容,是指挥员作战指挥决策活动的重要环节。科学合理地进行兵力编组,将兵力使用达到最优化,是提升部队战斗力,取得战斗胜利的关键。本文采用WBS方法将合成部队的战斗任务进行分解,然后运用基于兰彻斯特方程推导出的公式,构建了兵力编组的优化模型,具有较强的现实作用。
2 进攻作战对兵力编组要求
2.1 强调整体,符合意图
合成部队进攻作战兵力编组应充分考虑理解上级作战意图,结合本级作战任务,以作战全局的视角去考虑本级在作战全局中的地位和作用,不能计较一时的得与失,兵力编组一定要使本级能完成任务,达成作战目标。其次,可以将本级作战任务进行细化分解,依据各作战时节,将任务细分为多个子任务,便于部队完成。子任务的划分要有助于整体作战任务的完成。分析作战任务,对所需的战斗力量进行量化判断,合理科学地进行兵力编组配置,制定编组方案,使各作战单位有能力完成计划任务。
2.2 模块编组,功能耦合
合成部队进攻作战,是信息化条件背景下的联合作战,战场形势瞬息万变,各作战编组在任何作战地点,在任一作战时节,都有可能主导战斗进程,改变战场形势。各编组要合理编配作战力量,适应如指挥协同高效,较强机动能力,能够隐蔽接敌,较强火力突击等作战要求。要实行模块化编组,各群队之间即相互独立,又能相互支援配合。要注意发挥编组的作战优势,相互间密切配合;又能扬长避短,发挥编组内各专业兵种、各要素的特长,形成一个有机的作战整体,实现力量互补、功能耦合,合成编组、战力倍增的效果。
2.3 利于指挥,便于协调
合成部队进攻作战兵力编组要有相应的指挥手段与之适应。战场上,敌我双方攻防激烈,指挥协同极易遭敌破坏和干扰。此外,合成编组内,参战要素多也会给指挥协调带来困难,各作战编组之间的指挥协调要求也是比较高的。在进行进攻作战时,通常以计划协调为主,根据形势变化,适时灵活协同。在进行部署时,要使各编组之间能简单高效地进行联络、协调,科学合理地确定指挥跨度,来保证合成旅整个作战的整体协调性[1~6]。
3 战斗任务分解
3.1 相关概念
1)任务分解
指挥员在接受作战任务后,根据上级意图、战场实际情况、本级作战能力,遵循相关规则,对本级任务进行细化分解。
2)子任务
指挥员将本级作战任务首先进行的第一次分解,该任务还能够被再次进行细化分解。
3)元任务
指挥员将受领的任务进行分解的终点,能够被各编组所独立执行。
4)作战资源
指合成部队进行进攻作战所有参战要素。
3.2 基于WBS的战斗任务分解
论文采用WBS进行合成旅进攻战斗任务分解,WBS分解情况如图1所示。
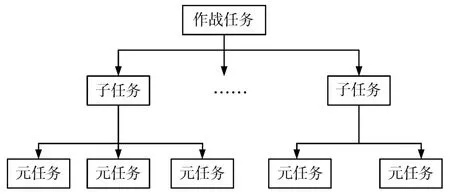
图1 WBS示意图
其中,战斗任务为合成部队进攻战斗任务,子任务为将进攻任务分解之后所得,底层为合成部队作战资源可单独完成的元任务[7~8]。
3.2.1 战斗任务分解原则
1)粒度原则
将任务进行最终分解成元任务,不可再进行下一层分解,可被作战资源单独执行。
2)百分百原则
作战资源百分百能完成元任务。
3)同层同标准原则
同一层作战任务分解都要是相同标准。
3.2.2 战斗任务分解方法
1)按阶段进行阵地进攻战斗任务分解
例如,可以按作战阶段将阵地进攻战斗任务分解为信息火力突击、立体连续冲击、抗敌攻势行动、驱歼纵深之敌、清除敌坚固目标和追击围剿残敌等阶段。
2)按地域进行阵地进攻战斗任务分解
例如,可以按照作战地域将阵地进攻战斗任务分解为前沿突击任务,后方防卫任务,纵深攻击任务等。
3)按功能进行阵地进攻战斗任务分解
可以按照作战功能将阵地进攻战斗任务分解为信火突击、火力打击、电子对抗等。
3.2.3 战斗任务分解过程
对合成部队进攻战斗任务进行分解需要多种分解方法。具体分解流程如图2所示。

图2 战斗任务分解流程图
4 构建兵力编组模型
1)明确参数符号
参数说明如表1所示。

表1 参数说明
2)设置模型变量
合成部队进攻作战兵力编组科学合理的关键在于能否对分解的最终元任务单独完成,因此,可把参与任务MTj的作战资源Zi数量qij,作为合成部队进攻作战兵力编组模型的变量。
3)确定约束条件
完成元任务所必须的资源数量应当小于其所对应的资源数量,即:

合成部队某类资源总量应大于完成某元任务所必须的该类型资源数量即:

4)建立目标函数
以完成合成部队进攻作战任务,己方损失最小为目标。我们以Lanchester平方率模型为基础,即

可得:

求得:
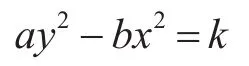
假设x0、y0分别表示敌我双方初始兵力,x、y的关系如图3所示。
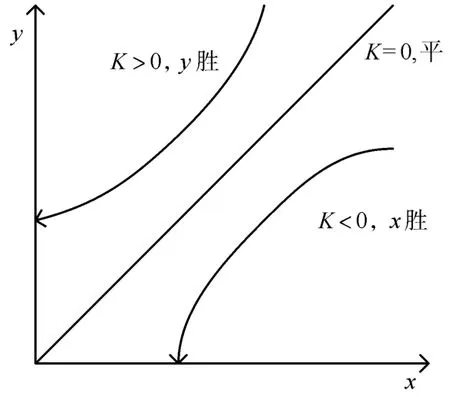
图3 Lanchester模型
(1)若我方任务完成,则剩余兵力为
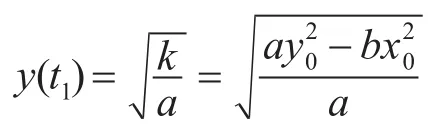
其中伤亡人数 ys为

以上是算得某一兵种伤亡人数,将其拓展到多兵种作战,可得:

最后可得伤亡总数为
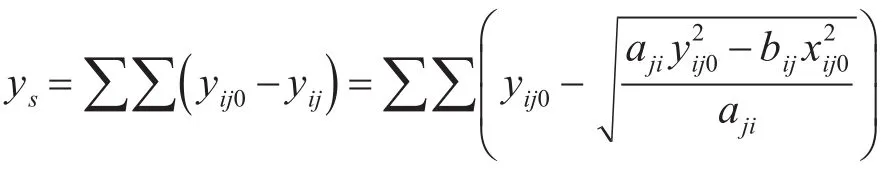
(2)合成部队进攻作战伤亡函数
将上式运用于合成部队进攻作战完成任务后伤亡情况,可得在完成某一作战任务之后的伤亡数量为
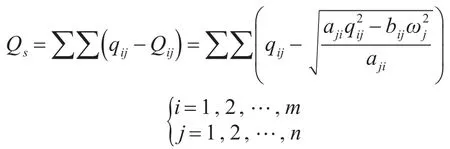
5)编组规划模型
定量T为作战结束时刻,任务完成之后,敌我双方兵力的剩余量为

多兵种作战资源剩余量为
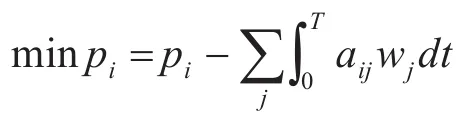
可构建合成部队进攻战斗兵力编组模型[9~12]:

5 结语
合成部队进攻战斗兵力部署是一个复杂问题,本文以合成部队进攻战斗为例,首先通过WBS对作战任务按照功能进行分解,然后通过Lanchester方程构建了兵力部署的优化模型,能较好地解决此类问题。通过模型构建,为参谋机关提供了参考,使指挥员在兵力部署决策时更加的科学合理,具有较高的现实意义。

