基于贝叶斯克里金的山东省小麦产量时空相依模型*
郭哲琦,孟生旺
(中国人民大学统计学院,北京市,100872)
0 引言
区域产量保险是农业指数保险的一个重要组成部分,选取某地区的单位农作物产量作为保险标的,当产量低于保障水平时保险公司即对农户进行赔付[1-5]。相较于依据实际损失定损赔付的传统农业保险,具有操作简便、降低道德风险和逆向选择的优势。但由于其通过借助其他地区数据和天气等数据提高样本量,导致区域间农作物产量、农作物产量与天气变量间的相依关系复杂交错。
区域产量保险保费的厘定依赖于农作物区域产量的分布。考虑到农作物产量随时间变化的趋势及区域产量间的空间相依特征,常用建模方法有两步法和嵌入式模型法。两步法首先通过使用线性趋势模型、ARIMA模型、自适应局部参数趋势模型等方法建立趋势模型,随后进行去趋势处理,最后对去除趋势后的农作物产量数据进行拟合。嵌入式模型基于分层模型,假定农作物产量服从特定分布并在分布参数中引入时间解释变量、天气变量和空间相依的随机效应等,通过参数间的时空相依性反应产量间的时空相依性。现有文献中,对农作物产量分布建模时多仅考虑时间因素或空间因素,且选用的分布多为简单的正态分布、威布尔分布或逻辑斯特分布等,并且仅对均值参数引入相依性。Annan等[6]研究发现由于气候、地质特征等的相似性,给定县的农作物产量往往与附近县的产量相似。Park等研究发现使用广义帕累托分布对农作物产量进行拟合能更好地反映其尾部特征。Ozaki等假定作物产量服从正态分布,对产量均值建立时间和空间自相关性建模。
实际上,农作物产量由于受天气、地理位置、土质条件等具有空间连续性因素的影响,相邻地区间产量必定存在空间相依性,并且随技术等因素的改进,产量也会随时间产生上升趋势,因此在建立产量模型时应同时考虑时空相依性;受高温、霜冻、飓风等灾害影响,农作物产量数据会呈现偏态、峰值等非正态特征,混合分布和广义分布可以为此提供更大的灵活性;不同解释变量可对农产量分布的均值、方差、偏度、峰度造成影响,可通过对尺度参数和形状参数分别引入不同的解释变量实现。本文在嵌入式贝叶斯模型的基础上,采用广义贝塔Ⅱ型分布(Generalized Beta Distribution of the Second Kind,简称GB2分布)拟合农作物产量分布,在其形状和尺度参数中分别引入时间效应和克里金方法以描述区域间的时空相依关系,并引入经纬度、历史产量等协变量增加模型可解释性。
1 统计模型
1.1 广义贝塔Ⅱ型分布
农作物产量建模需要建立在分布假设的基础上,包括参数分布、非参数分布、半参数分布等。GB2分布[3]是一种四参数的连续性分布,其密度函数如式(1)所示。用随机变量Y表示农作物产量。
(1)
式中:b——尺度参数,b>0;
a——形状参数,a∈R;
p——偏度参数,p>0;
q——峰度参数,q>0;
B(p,q)——贝塔函数。
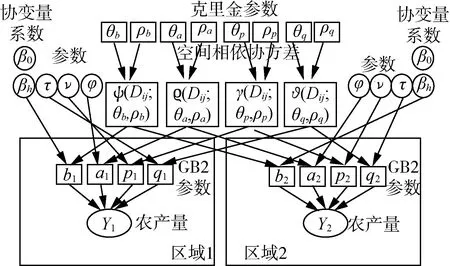
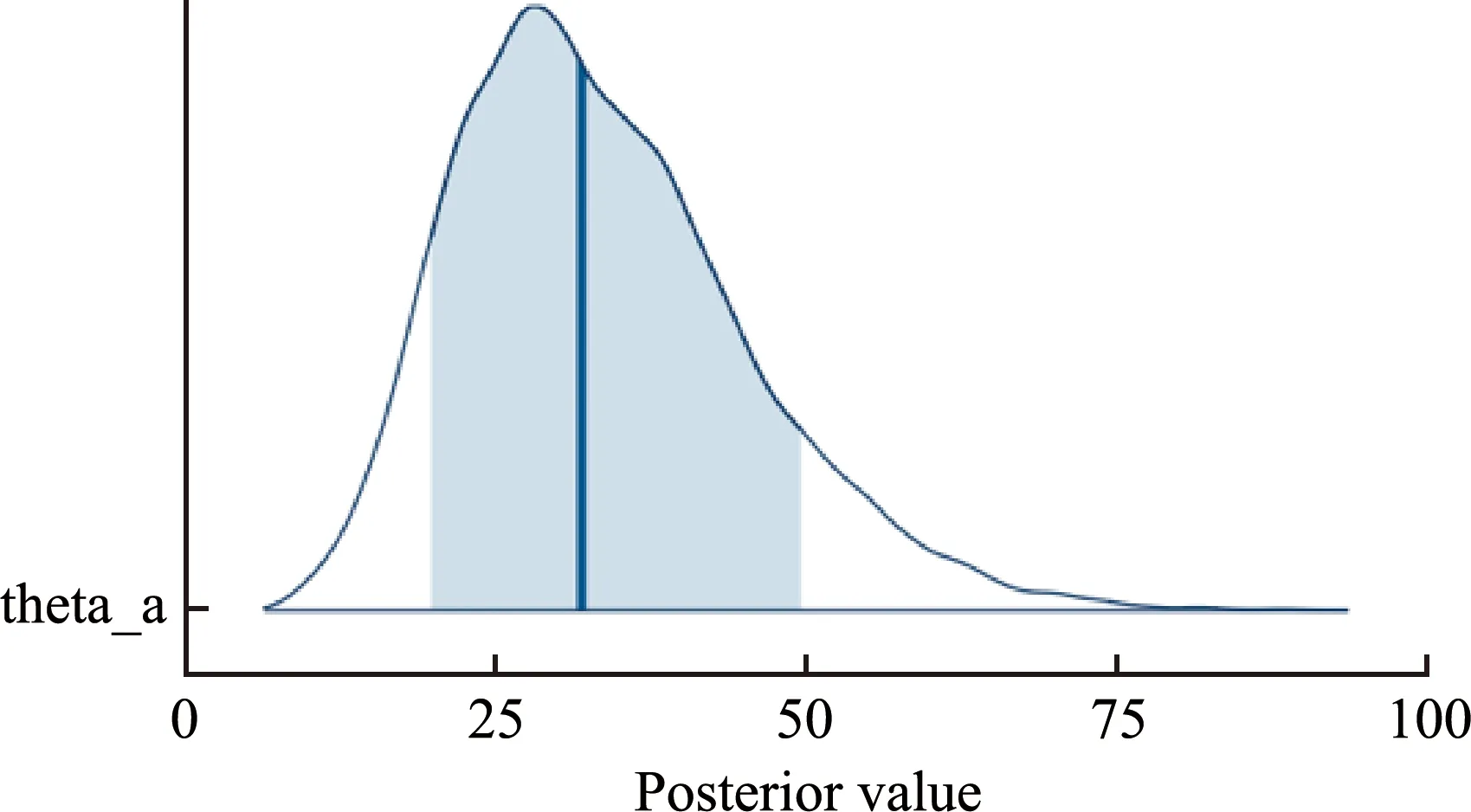
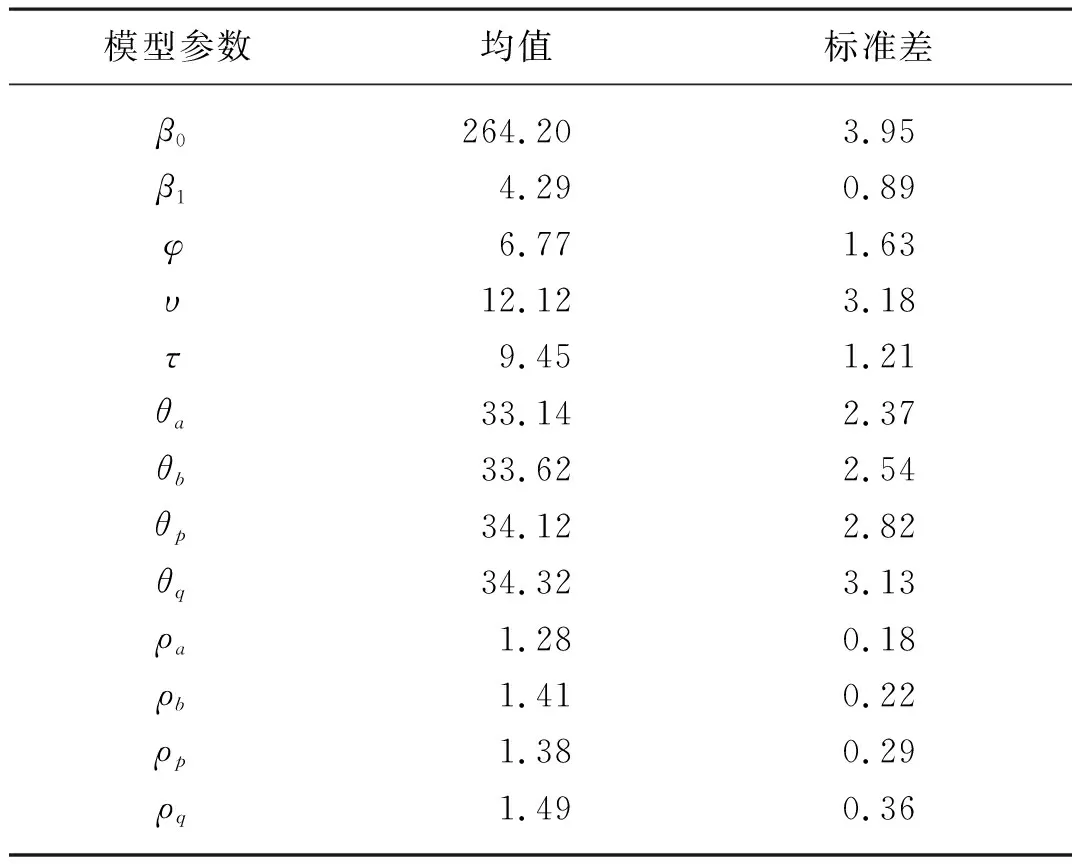
当ap>1且-ap<1 (2) (3) 其风险度量——风险值(VaR)和尾部条件期望(TCE)可借助贝塔分布求得。 (4) (5) 当参数a,b,p,q取特定值时,GB2分布可退化为其他分布类型,如常见的伽马分布、威布尔分布、对数正态分布等,涉及的分布如图1所示。 由此可见GB2分布具有较强的灵活性,对多峰、轻厚尾数据均可进行处理[4]。本文所关注的农作物区域产量分布具有厚尾的非正态特征,适用GB2分布来改进其拟合效果。 图1 GB2分布族Fig. 1 GB2 distribution 本文使用的嵌入式产量模型基于贝叶斯理论中的贝叶斯层次模型[5],该模型拥有三层结构。第一层为似然层(Likelihood Layer),各区域农作物产量服从特定分布;第二层为过程层(Process Layer),对产量分布参数引入协变量,包括时间、历史产量、经纬度、空间协变量等,从而体现农作物产量的时间趋势、空间异质性、空间相依关系等;第三层为先验层(Prior Layer),包含各超参数的先验分布。层次贝叶斯模型可写为 似然层:Y|Ω1,Ω2~p1(Y|Ω1,Ω2) (6) 过程层:Ω1|Ω2~p2(Ω1|Ω2) (7) 先验层:Ω2~p3(Ω2) (8) 式中:pj——各层相关的密度函数; Y——所有区域的产量数据矩阵; Ω1——所有区域农作物产量分布参数的矩阵; Ω2——所有超参数组成的向量。 本文使用GB2分布拟合山东省各地市小麦产量,并引入农作物种植时间t、所处经纬度等作为协变量,同时引入克里金方法解释农作物产量在不同区域间的空间相依关系。 1.2.1 似然层 令yit为区域i=1,…,N在第t=1,…,T年的农作物产量,则似然层的概率密度函数 (9) 1.2.2 过程层 层次模型中最重要的部分为过程层,体现了农作物产量受协变量影响的具体形式。对于GB2分布的尺度参数 bi=μi+εi (10) 式中:μi——高斯空间过程的关键部分; Xhi——区域i的协变量; b——尺度参数向量,b=[b1,…,bN]′,且服从多元高斯空间过程; ψ(Dij;θb,ρb)——空间协方差矩阵,区域i,j间欧式距离Dij的函数,θb,ρb为b的克里金参数; εi——误差项; Λ——对角线元素是ω2且其他元素是零的对角矩阵。 类似的,对GB2分布的形状参数ai,pi,qi分别有 ai=φ+εi (11) 式中:φ——常数; a——形状参数向量,a=[a1,…,aN]′; Ψ——对角线元素是ο2且其他元素是零的对角矩阵。 pi=ν+εi (12) 其中,p~MVGP(ν,∑p);∑p=γ(Dij;θp,ρp);εi~MVN(0,Μ)。 式中:ν——常数; p——形状参数向量,p=[p1,…,pN]′; γ(Dij;θp,ρp)——空间协方差矩阵,θp,ρp为p的克里金参数; Μ——对角线元素是ζ2且其他元素是零的对角矩阵。 qi=τ+εi (13) 其中,q~MVGP(τ,∑q);∑q=ϑ(Dij;θq,ρq);εi~MVN(0,Κ)。 式中:τ——常数; q——形状参数向量,q=[q1,…,qN]′; ϑ(Dij;θq,ρq)——空间协方差矩阵,θq,ρq为q的克里金参数; K——对角线元素是κ2且其他元素是零的对角矩阵。 由此可知,Ω1=[a,b,p,q],Ω2=[β0,βh,φ,ν,τ,θa,ρa,θb,ρb,θp,ρp,θq,ρq]′。 假设每个GB2分布参数的空间过程独立,因此 (14) 1.2.3 先验层 使用贝叶斯方法进行参数估计,需要对模型的先验参数进行设定。由于没有任何GB2分布参数与协变量间关系的信息,因此选取β0、βh的先验分布为均匀分布Uniform(-10 000,10 000)。对于克里金参数(θ,ρ)而言,不恰当的先验分布对后验分布具有较大影响,Banerjee,Carlin,and Gelfand(2004)推荐对克里金参数选用信息先验。因此,本文使用极大似然估计,由经验信息得到ρ的先验分布,并借由区域间的经纬度信息得到θ的先验分布。假定先验层中的所有超参数互相独立,因此 p3(Ω2)=p(β0)p(βh)p(φ)p(ν)p(τ)p(θa) p(θb)p(θp)p(θq)p(ρa)p(ρb) p(ρp)p(ρq) (15) 模型参数的联合后验分布 p(Ω1|Ω2|Y)∝p1(Y|Ω1,Ω2)p2(Ω1|Ω2)p3(Ω2) (16) 拟合农作物产量分布的层次贝叶斯模型结构可通过图2有更直观的了解。 图2 使用克里金方法的贝叶斯层次结构简图Fig. 2 Schematic of the Bayesian hierarchicalstructure using Kriging method 运用哈密尔顿蒙特卡洛算法(Hamiltonian Monte Carlo,简称HMC)[8]从公式(16)的后验分布中模拟获得参数的随机样本,这些样本根据目标概率收敛到某个分布,从而得到相应参数的若干统计量、置信区间以及预测分布等。HMC是一种MCMC算法,与传统的Gibbs抽样和MH抽样相比,采样更加快速,可通过用以建立贝叶斯模型的软件STAN实现[9-17]。 本文选用山东省各地区的小麦产量数据,构建基于贝叶斯克里金的嵌入式时空模型对小麦产量进行拟合预测,并据此计算山东省各地区的区域产量保险费率。 本文选用山东省各地市1988—2019年的小麦平均产量数据。去除存在行政区划变动的3个地区后,剩余14个地区(济南、青岛、淄博、枣庄、东营、烟台、菏泽、聊城、德州、临沂、威海、泰安、济宁、潍坊)共计448个数据,不存在缺失值。数据来源为山东省统计年鉴。14个地区的小麦单产数据随时呈明显递增趋势,大致为线性关系,且对1988—2019年各地小麦平均单产数据构建空间分布图后发现其呈一定程度的聚集状态。 应用1988—2018年山东省各地市小麦产量数据对各模型进行拟合,并应用2019年数据检验各模型预测效果。最优模型的选择采用DIC准则,模型预测效果则通过RMSE进行度量,通过R软件的rethinking包实现。 (15) 表1 小麦产量模型DIC值Tab. 1 DIC value of wheat yield model 表2 模型2预测误差Tab. 2 Prediction result using RMSE of model 2 使用1988—2019年的小麦产量数据,应用嵌入式时空相依模型和HMC算法可得到模型2的参数估计结果(表3)和部分克里金参数后验密度(图3)。Rstan包为这一过程的实现提供了便捷的方式,设定马尔可夫链数为4,每条链模拟10 000个样本,剔除前2 000个样本。由表3的模型2参数估计结果可见,产量的尺度参数随时间递增,各参数的同一克里金参数相差不大。 (a) θb后验密度图 (b) ρb后验密度图 (c) θb轨迹图 (d) ρb轨迹图 (e) θa后验密度图 (f) ρa后验密度图 (g) θa轨迹图 (h) ρa轨迹图图3 克里金参数后验密度Fig. 3 Posterior densities of Kriging parameters 此外,通过得到的克里金参数的后验密度(图3)可进一步计算模型的变异函数,从而直观反映不同地区间GB2参数的空间相依关系。变异函数中的横轴表示地区间的距离,纵轴表示该距离下的变异函数,变异函数为零表明完全相依,变异函数越大表明空间相关性越小。 当变异函数进入平稳状态时,所对应的距离为变程参数值,表明空间相关性对GB2参数的影响保持在此范围内。 变异函数趋于平稳时的值为基台参数值,反映了GB2参数的最大差异性。从而可较直观的阐明小麦产量分布参数的空间结构。 表3 参数估计结果Tab. 3 Estimated parameters 山东省小麦区域产量保险费率使用两种方法进行厘定,分别为本文所建立的基于GB2分布的嵌入式时空模型和传统的两步法,即先对各地区小麦产量数据进行趋势拟合,随后进行去趋势处理,再用去趋势后的数据对各地区分别拟合GB2分布。不同保障水平λ下的各地区保费如表4所示。 表4 75%和90%保障水平下的山东省各地区小麦区域产量保费Tab. 4 75% and 90% coverage level premiums of area cropyield insurance for cities in Shandong % 传统两步法所得费率依赖于各地区历史产量数据,具有较大的波动性,费率最高的菏泽为5.4%,而最低的淄博为2.8%;克里金方法的引入使得各地区产量分布间相依性更加明显,费率最高的为4.5%,最低为3.2%,相比而言费率变化更加平滑且适度有所降低。 由图4可以看出,相比于传统的两步法,基于克里金方法的嵌入式时空模型法具有更强的空间聚集性。嵌入式时空模型由于其空间相依性与距离相关,因此区域产量保险费率呈现聚集性状态,而两步法的费率空间特征则因地区和农作物品种不同没有特定规律。 (a) 克里金法 (b) 两步法图4 75%保障水平下的克里金法、两步法保费Fig. 4 75% coverage level premiums from Kriging andtwo-step method 农作物产量预测在指导农业生产及确定农业保险费率方面具有重要意义。产量受土壤、气候、技术等因素的影响存在时间趋势、空间异质性、空间相依性,本文基于贝叶斯理论框架,在产量分布的参数中嵌入时间变量以体现农作物产量数据随时间变化的趋势、引入贝叶斯克里金方法体现地区间的空间相依特征、引入多种协变量增加模型可解释性,并采用GB2分布处理产量分布的偏态及多峰特征。结果表明,本文所构造的基于贝叶斯克里金的嵌入式时空模型,通过增大样本量的方法提高了估计的稳定性,对山东省小麦产量分布的拟合预测效果良好,对产量分布间的空间相依特征进行了体现,且具有较好的可解释性;进一步使用该模型厘定的区域产量费率相较于传统方法所得的费率而言整体有所降低,地区最高费率为4.5%,最低为3.2%,较低且均衡的费率增强了农户投保积极性,可为保障粮食安全和促进现代农业发展提供助力。

1.2 嵌入式产量模型



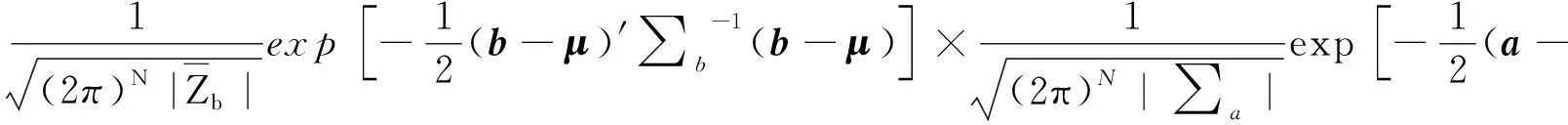
2 实证分析
2.1 数据描述
2.2 建立时空相依模型











2.3 保费计算



3 结论

