应用于茶叶罐分拣的码垛机器人最优关节空间控制*
季晓明,文怀海,刘艳梨
(1. 江苏安全技术职业学院电气工程系,江苏徐州,221011; 2. 大连理工大学机械工程学院,辽宁大连,116024;3. 南京航空航天大学机电学院,南京市,210016)
0 引言
罐盒分拣是茶叶自动包装技术中的重要一环。随着智能制造、机器视觉、机器人等技术的发展,运用码垛机器人来提高自动包装生产线的作业效率越来越受到用户的关注[1-2]。对于码垛机器人的研究通常集中在本体设计、动力学、控制系统设计与轨迹规划几个方面[3],而本文研究内容为关节空间内码垛机器人的最优轨迹跟踪控制。机器人系统具有高非线性、多变量、高维度的特性,这给高精度控制器的设计带来了很大的难度。再者,由系统摩擦力矩、关节负载、外界扰动与未建模特性构成的集总干扰力矩也会进一步加剧控制器设计的难度。
对于上述问题,国内外学者已进行了诸多探索。例如,Atalar-Ayyldz等[4]采用分数阶PID(Proportion Integration Differentiation,PID)控制策略来设计6自由度机器人的轨迹跟踪控制器,在仿真环境下获得了不错的控制效果。Nikdel等[5]设计了一种状态增强自适应反步法(Backstepping controller,BC)控制器来保证串联型机器人在非线性与参数不确定性下的跟踪性能,并成功应用到了大型工业SCARA机器人的仿真中。针对系统中的集总干扰力矩,Homayounzade等[6]将BC和扰动观测器相结合有效补偿与抑制了干扰项,提高了机器人轨迹跟踪的精度。这些控制策略为本文提供了很好的借鉴。近年来,滑模控制(Sliding mode control,SMC)技术颇受人们关注,它是一种常见的鲁棒控制技术,被广泛应用于机器人控制系统设计中。不过传统的SMC因其固有的滑模面结构易引起控制信号的抖振,在一定程度上会削弱系统的控制性能[7]。因此,本文采用快速连续非奇异终端滑模面来改进传统SMC,提高机器人系统状态量的收敛速度。另一方面,码垛机器人轨迹跟踪效果还依赖于参考轨迹的规划。对于关节空间的轨迹规划,本文先用萤火虫算法(Glowworm swarm optimization algorithm,GSO)计算出码垛机器人起止位形对应的关节角,接着用五阶多项式插补获得关节角序列。为了保证算法的实时性,中间插值点不能过多,但这也会带来关节不光滑的后果,因此引入NUBRS曲线进行光滑处理,使得关节运动平滑柔顺。最后,通过两组仿真算例对本文所提方法的有效性进行验证。
1 码垛机器人设计与动力学建模
1.1 系统设计
本文设计了一条码垛机器人生产线来提高不同颜色茶叶罐的分拣效率,如图1所示。整条生产线的工作原理为:深浅两种颜色的茶叶罐倒入下料筒中,在输送带A上经视觉检测,深色茶叶罐落入落料盒A中,浅色茶叶罐由码垛机器人搬运至输送带B上,落入落料盒B中。
1.2 机器人动力学建模
对于图1所示生产线中的码垛机器人,可采用拉格朗日方程推导出刚体动力学模型[8]
(1)

M——R6×6刚度矩阵;
C——R6×6包含科氏力与离心力的矩阵;
G——R6×1重力项矩阵;
τ——R6×1的关节力矩;
τd——R6×1的包含了摩擦力矩、关节负载、外界扰动与未建模特性的集总干扰力矩。
为更好地展示机器人系统输入输出的关系,将式(1)改写成
(2)
2 码垛机器人最优运动控制
2.1 轨迹规划
假设码垛机器人末端执行器的实际位形为(Rd,Pd),目标位形为(Rf,Pf),那么轨迹规划的本质就是引入GSO算法使得下列的目标函数最小[9]。
(3)
算法的具体过程如下。
1) 算法初始化。设GSO的种群数目为N,随机产生i只萤火虫的位置,即
qi(t)=qL+rand(0,1)·(qU-qL)
(4)
式中: rand(·)——0~1之间的随机函数;
qU、qL——关节空间的上限、下限;
t——迭代次数。
2) 更新决策阈。萤火虫群体间的信息交互能力是通过决策阈大小来决定的,决策阈的更新公式为
(5)
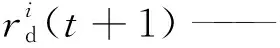
rs——最大感知半径;
β——权重因子;
nt——控制参数;
Ni(t)——第i只萤火虫在第t次迭代时邻域集合,满足约束条件见式(6)。
(6)
式中:gj(t)——邻域内第j只萤火虫位置;
li(t)、lj(t)——两只萤火虫的荧光素值。
3) 更新萤火虫位置与荧光素值。比较当前萤火虫和邻域萤火虫之间的荧光素值大小,种群选择朝荧光素值较大的萤火虫方向移动,移动的概率为
(7)
第i只萤火虫的位置更新公式为
(8)
式中:s——步长大小。
荧光素值的大小取决于目标函数值的大小,其更新公式为
li(t)=(1-ρ)li(t-1)+γf(gi(t))
(9)
式中:ρ——0~1的常数,表示荧光素挥发值;
γ——荧光素值的更新速度。
4) 终止条件。在邻域集合内,萤火虫i遇到荧光素值更高的萤火虫j时,若两者距离小于感知半径,则前者以概率Pij(t)选择邻域个体并其靠拢。接着,萤火虫i更新位置与荧光素值,直到算法迭代次数等于最大值Tmax,算法终止。
通过上述GSO算法就可以获得码垛机器人的运动学逆解。为了使机器人在关节空间内运动光滑连续,还需对关节角序列做光滑处理。这里引入NURBS曲线结构[10],其公式为
(10)
式中:Pi——控制顶点数;
ωi——权重因子,ωi≥0;
Ni,k(u)——k-1次的B样条基函数;
a、b——设定为0和1;
u——节点参数,满足约束条件见式(11)。
(11)
2.2 控制器设计
当获得关节角的参考轨迹后,将设计机器人的关节空间轨迹跟踪控制器,该控制器设计思想为:不依赖机器人精确的动力学模型,仅根据系统输入输出数据来构造控制律[11]。
具体过程如下。
(12)
(13)
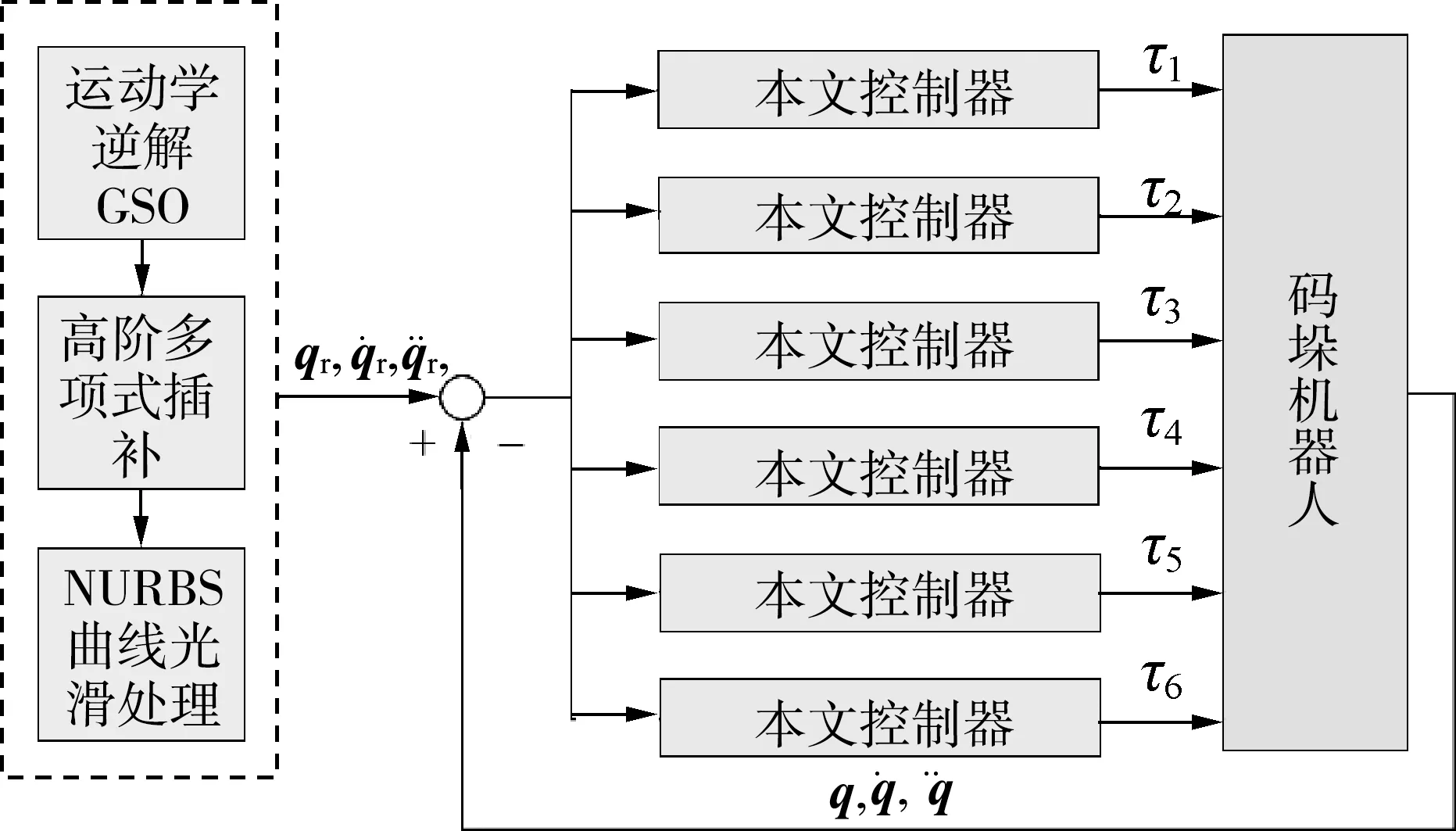
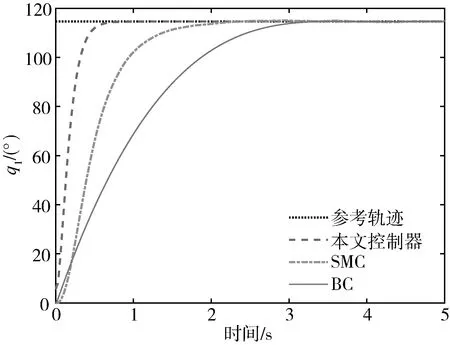
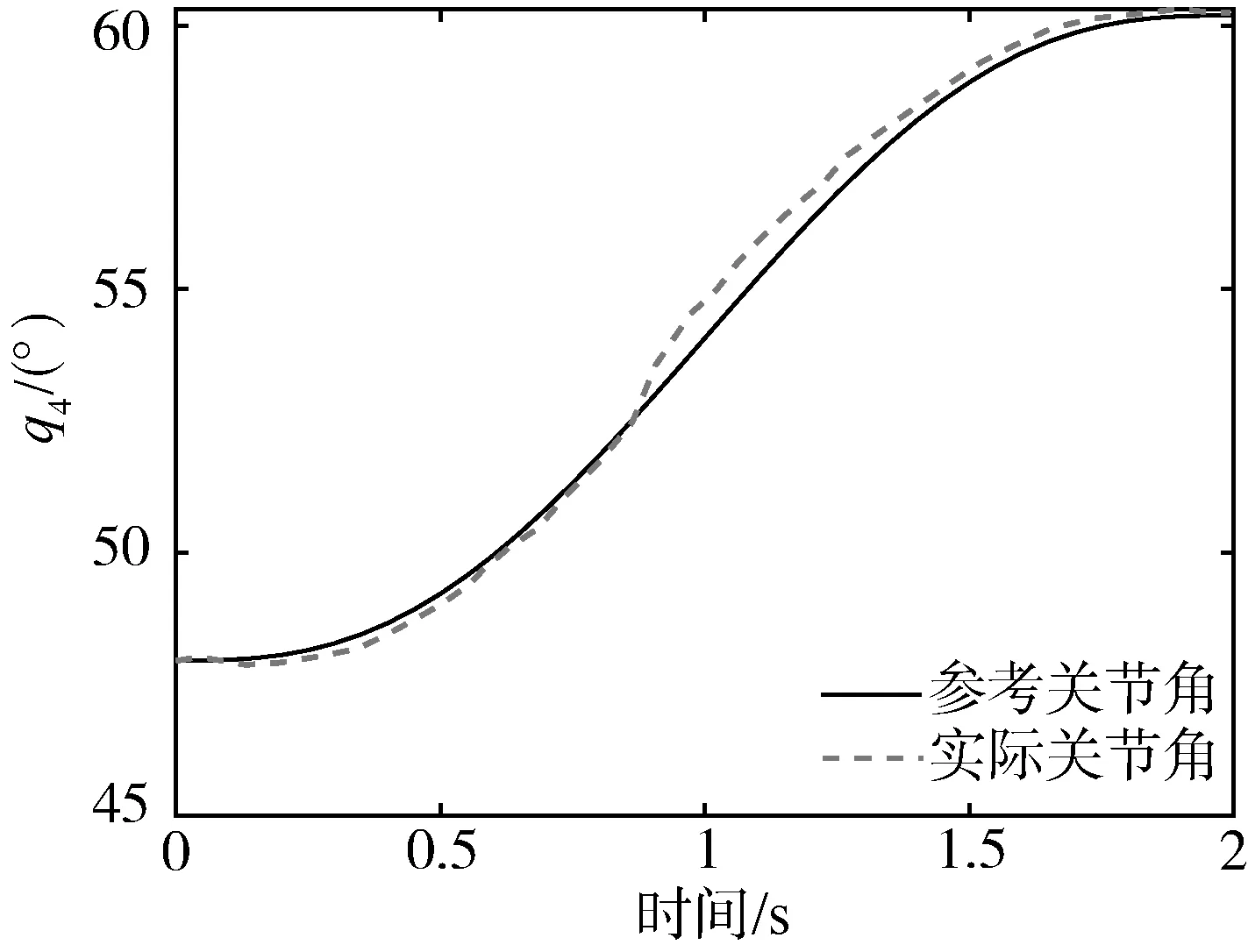
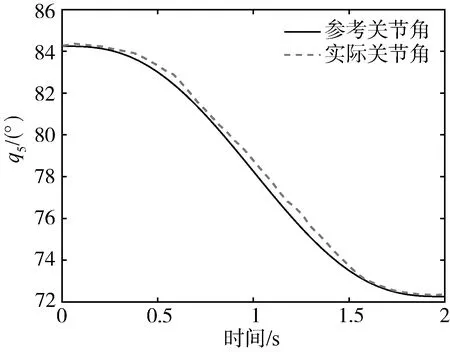
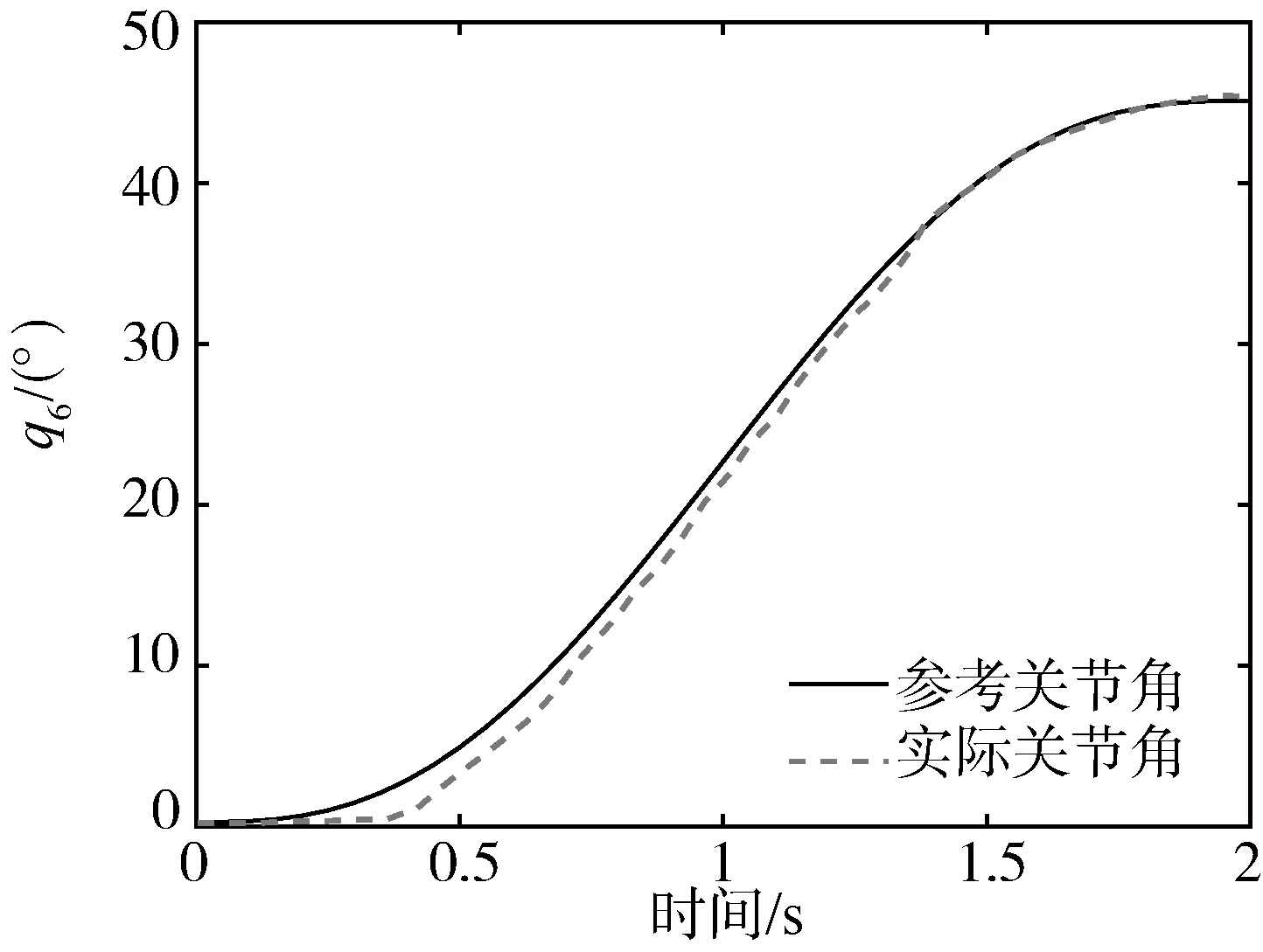
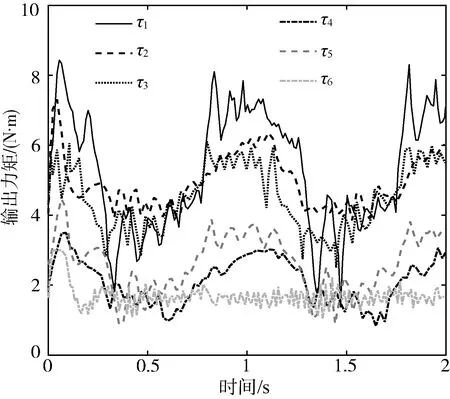
其中1<γ<2,0 式中:β、k1、k2——控制增益矩阵。 求式(12)关于时间的一阶导数,并联立式(13)可得码垛机器人的控制律为 (14) 式(14)中控制律包括等效控制律τe和趋近律τr两部分。其中,τe用于抑制控制器的抖振和减弱干扰力矩的影响,以保证系统的鲁棒性;τr用于加快系统各状态量的响应速率,提高系统的被控性能。 假设机器人系统中的集总干扰τd有界且可导,则在本文所设计控制器作用下能够保证关节变量跟踪误差以及其一阶导数在有限时间内收敛到某个区域[12],即 |e|≤2Δ=2min(Δ1,Δ2) (15) (16) 选择李雅普诺夫函数为 (17) 对式(17)求关于时间的一阶导数有 (18) 联立式(12)~式(14),可得连续非奇异终端滑模面函数的一阶导数为 (19) 联立式(17)~式(19)可得李雅普诺夫函数的一阶导数为 式(20)包含两种形式,即 (21) 引理:如果存在李雅普诺夫函数V不等式(22),则其收敛到初始值V(0)所需的时间为 (22) ts≤ω-1(1-ζ)-1ln(1+ωp-1V01-ζ) (23) 其中ω、p>0且0<ζ<1。 (24) (25) 整理式(25),有 |s|≤Δ=min(Δ1,Δ2) (26) 进而,将滑模面变换成如下形式 (27) 由于|s|≤Δ,因此关节角跟踪误差的一阶导数能在有限时间收敛到区域 (28) 本文所提方法的结构框架如图2所示。 图2 本文所提方法的结构框架Fig. 2 Structure frame of the proposed method 为验证本文所提方法的有效性,在Matlab/Simulink环境下进行仿真模拟。其中,码垛机器人的DH参数如表1所示,末端执行器(夹爪,用数字7表示)的长度为108 mm。 表1 码垛机器人的DH参数Tab. 1 DH parameters of the palletizing robot 为了比较本文所提控制器的性能,引入SMC和BC进行比较(这两种控制器参数的定义可参见文献[13-14],与本文控制器一样,它们也由GSO算法进行参数整定),三种控制器的参数如表2所示。以q1为例,设定其需要跟踪的参考轨迹为q1r=114.6°,τd1=50 sint,仿真时间为5 s,其余初始条件均为0,结果如图3所示。 表2 三种控制器的参数Tab. 2 Parameters of the three controllers 图3 三种控制器下关节角1的跟踪响应Fig. 3 Tracking response of joint 1 withthree controllers respectively 从图3中可以看出,三种控制器均能帮助机器人关节角q1跟踪上参考轨迹,但本文控制器的稳定时间小于0.5 s,且稳态误差不大于2%,这说明本文控制器能在集总干扰力矩影响下提供相对稳定的输出响应,从而证明了本文控制策略的优越性。 进而设计第二个仿真算例来模拟码垛机器人对茶叶罐的分拣。设经视觉检测模块测量的红色茶叶罐位形为[0.617,0.917,1.256]Tmm,[-40°,46°,99°]T,需要码放的目标点位形为[0.090,-0.518,1.664]Tmm,[145°,92°,-160°]T。仿真中,先根据机器人末端执行器的起始位形用GSO算法计算出起始关节角,再经五阶多项式插值法获得关节角空间中的运动序列,并用NURBS曲线进行平滑过渡处理,最终生成机器人关节轨迹。 GSO算法参数设置如下:N=20,γ=0.6,ρ=0.4,s=0.03,β=0.1,nt=8。GSO算法的迭代曲线如图4所示,算法所需时间为0.37 s,完全能够满足码垛机器人的工作节拍。 图5给出了规划后的机器人关节轨迹,可以看出在执行码垛任务时各关节角变化较为平稳柔顺。 最后利用本文所设计控制器去跟踪上述规划好的关节轨迹。选择均值为0、方差为0.01、频率为20 Hz、增益为10的随机噪声来模拟集总干扰力矩。表3给出了码垛机器人系统控制器参数。仿真结果如图6所示。 图4 GSO迭代曲线Fig. 4 Iteration curve of GSO 从图6中可以看出,在本文控制器作用下机器人能够较好地抑制住集总干扰力矩,使得各关节跟踪上参考轨迹。进而,以均方根误差(Root Mean Square Error,简称RMSE)[15]来量化关节空间内的跟踪误差,各关节角的RMSE分别为0.025,0.031,0.087,0.103,0.154,0.160,这种量级误差在实操中是可接受的。 图7给出的各关节角控制力矩没有明显的抖振现象,这说明本文所提含有饱和函数的连续非奇异终端滑模面函数具有良好的抖振降低效果,进一步说明了所设计控制器的有效性。 图5 轨迹规划后的关节角序列Fig. 5 Joint angles response after trajectory planning 表3 本文控制器参数Tab. 3 Parameters of the proposed controller (a) 关节角1的响应 (b) 关节角2的响应 (c) 关节角3的响应 (d) 关节角4的响应 (e) 关节角5的响应 (f) 关节角6的响应图6 本文控制器下关节角的跟踪响应Fig. 6 Tracking response of joints with the proposed controller 图7 关节力矩响应Fig. 7 Response of the torque 针对茶叶罐分拣码垛机器人的关节空间控制,本文提出了一种基于快速连续非奇异终端滑模策略的轨迹跟踪控制方法。该方法根据码垛机器人输入输出数据分别设计6个独立的控制器,利用快速连续非奇异终端滑模面来提高系统状态量的收敛速度,然后基于李雅普诺夫函数证明所设计的控制系统全局稳定,最后通过仿真算例对本文方法进行了验证。 1) 与SMC和BC相比,本文控制器跟踪性能最好,并且稳定时间小于0.5 s,稳态误差不大于2%。 2) 本文控制器能有效抑制集总干扰力矩影响和削弱控制抖振,能保证机器人在关节空间内的高精度轨迹跟踪控制。 3) 结合GSO算法、五阶多项式插补法与NURBS曲线能快速帮助码垛机器人规划出光滑柔顺的关节运动轨迹,算法所需时间为0.37 s,实时性较高。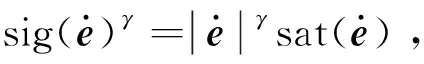

2.3 稳定性证明

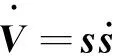
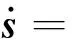
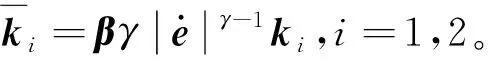


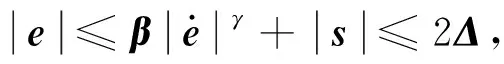
3 结果与分析








4 结论

