基于堆叠式LSTM与熵值法的苹果价格组合预测模型研究*

王晓蕾，张艳，柳平增，温孚江，郑勇，王刚

(1. 山东农业大学信息科学与工程学院，山东泰安，271000； 2. 山东省现代农业农村发展研究中心，济南市，250100；3. 德州市陵城区农业农村局，山东德州，253500)

0 引言

我国是世界上最大的苹果生产国和消费国，苹果已成为部分农民增收致富的支柱产业，受供求、季节和自然灾害等因素的影响，苹果市场价格波动愈发显著，价格波动直接影响着苹果产业从业者的收益。开展苹果市场价格的短期预测，对果农规避市场风险，以及对稳定农业生产、平衡物价水平、保障消费者福利水平至关重要，也是制定农业产业政策、维护市场健康发展的重要依据。

从农产品价格预测方面来看，学者们主要从两个方面进行了探讨：一是基于传统的时间序列、神经网络以及机器学习等单个模型进行预测；二是使用组合模型进行农产品价格预测。单模型方面，早期的农产品价格预测方法主要为时间序列预测，因ARIMA能较好的拟合时间序列，因此多采用ARIMA系列模型进行价格预测[1-3]。ARIMA模型未能完全提取季节因素特征，利用季节分解方法剔除季节因素后[4]，再利用非平稳时间序列模型进行预测分析能得到更好的预测结果[5]；神经网络的自学习以及可灵活考虑多输入因素等特点[6-8]，能充分考虑影响价格的种植面积、产量及自然灾害因素，近几年被广泛应用于农产品价格预测[9]。组合模型方面，与神经网络中的各类模型相结合的组合模型，在价格预测模型中扮演着越来越重要的角色[10-13]。利用神经网络能提取更深层次的序列特征等优点，整合其他机器学习模型等预测特点[14-15]，能够满足对预测精度进一步提高的要求[16-17]。价格预测模型方面，部分学者从两方面对LSTM神经网络模型开展了研究，一是使用LSTM模型对价格时序进行预测[18-19]，利用改进和优化后的LSTM来提高预测精度[20-22]；二是采用与LSTM相结合的组合模型进行价格预测也能达到很好的效果[23-24]，其中LSTM-BP与LSTM-RNN组合模式被广泛应用于趋势预测、特征信息融合及语义分类等[25]。

综上研究结果发现，与神经网络相结合的组合模型在农产品价格预测方面具有显著性优势，且价格的空间传导效应对价格波动产生明显的影响。本文拟采用基尼系数与Granger因果关系检验分析苹果价格空间传导效应，并利用空间Markov链分析苹果价格的空间动态演进。为提高苹果价格的预测精度，采用熵值法客观提取价格空间传导效应特征信息，与改进后的堆叠式多层LSTM相结合来预测苹果价格。最后，基于堆叠式多层LSTM对苹果价格进行预测，并分析验证预测结果的准确性。

1 数据来源与研究方法

1.1 数据来源

本研究使用的数据源自中华人民共和国商务部创办的全国农产品商务信息公共服务平台，选取全国共99个农产品批发市场苹果价格，利用各省农产品市场的富士苹果日均价格进行空间传导效应分析，并预测山东富士苹果日均市场价格，单位为元/kg，选取区间为2014-01-01至2020-12-31。

1.2 研究方法

1.2.1 地区差距

采用基尼系数对全国各省苹果价格的地区差距进行分析，基尼系数(GINI)[26]的定义如式(1)所示。

(1)

式中：k——区域划分数；

nj——j区域内省份数；

nh——h区域内省份数；

yji——j区域内i省份的苹果价格；

yhr——h区域内r省份的苹果价格；

μ——全国各省份苹果价格平均值；

n——省份数。

1.2.2 Granger因果关系

为验证苹果价格的空间传导特征，采用Granger因果关系检验进行分析。Granger因果关系检验多被用于验证经济变量时间平稳序列之间的因果关系，其原理是假设一个省份苹果价格序列Xt的变化能够导致另一个省份苹果价格序列Yt的变化，且Xt的变化发生在Yt之前，则称Xt是Yt的Granger因，Yt是Xt的Granger果；反之亦然。对Granger因果关系检验进行估计如式(2)所示。

(2)

式中：α、β——被估计参数；

ε——残差序列；

θ——滞后阶数。

1.2.3 空间Markov链

空间Markov链方法是将“空间滞后”这一概念引入Markov分析过程中所得到的，如式(3)所示。利用该模型可以考察相邻省份的苹果价格对本省份苹果价格状态转移的影响。其具体方法是通过设定空间权重矩阵，把N×N的转移概率矩阵分解为N×N×N的转移概率矩阵，从而状态转移概率Pij表示为某省份由a时期的i类型转移到a+1时期的j类型的概率，以此揭示空间效应对苹果价格动态演进的影响。

P{Xa=j|Xa-1=i,Xa-2=ia-2, …,X0=i0}=

P{Xa=j|Xa-1=i}=Pij

(3)

式中：Pij——状态转移概率；

i，j——状态；

X——随机变量。

1.2.4 熵值法

熵值法是一种客观赋权方法，它通过计算多个特征的信息熵，根据各项特征信息的相对变化程度对苹果价格整体的影响来决定各项系数的权重，例如，相对变化程度大的特征项具有较大的权重。指标的信息熵值与权重分别如式(4)、式(5)所示。

(4)

(5)

式中：ej——第j项指标的熵值；

m——地区数；

Yij——第i个地区的第j个指标的数值；

Wj——指标权重。

1.2.5 长短期记忆模型

长短期记忆模型LSTM是一种时间递归神经网络，能解决RNN的梯度消失和梯度爆炸问题，能够用来预测特征间隔长、延迟长、具有滞后空间效应的苹果价格数据。LSTM的核心思想是门控逻辑，内部结构如图1所示。LSTM由遗忘门、输入门和输出门组成，其中遗忘门通过sigmoid函数取舍，决定对前一时刻状态的遗忘程度，如式(6)所示，其中，ft介于0与1之间。

ft=σ(Uf×Xt+Wf×ht-1+bf)

(6)

式中：σ——sigmoid函数；

U、W——变量的权重；

Xt——输入变量；

h——输出变量；

b——截距项。

输出门首先利用激活函数和激励函数筛选、保存输入变量并创建新向量，通过旧细胞状态与新变量更新细胞状态。如式(7)所示，其中，it取值为0或1。

it=σ(Ui×Xt+Wi×ht-1+bi)

(7)

tanh——正切激励函数；

ct-1——旧细胞状态值；

ct——新细胞状态值；

ft——遗忘程度。

式(8)中输出门根据激活函数确定输出变量，并利用激励函数处理细胞状态。

ot=σ(Uo×Xt+Wo×ht-1+bo)

ht=ot×tanh(ct)

(8)

式中：ot——输出门激活函数；

h——输出变量。

LSTM是由记忆块而不是神经元组成的，通过一个存储单元和三个控制门使得LSTM能够更好地选择数据并学习，对时间间隔长的有效历史信息形成记忆。随着信息量的增加，LSTM模型能够有效地学习预测已实现的价格波动所需的特征，让价格数据中的关键信息进行有效的更新和传递，能更好地捕捉苹果市场价格波动规律，从而提高对苹果市场价格的预测准确性。

图1 LSTM模型结构Fig. 1 LSTM model structure

2 空间传导效应分析

2.1 苹果价格地区差距

供求关系是影响苹果价格波动的重要因素，因供需关系而引起的苹果价格地区差距会造成地区内苹果市场供求失衡，利用基尼系数公式求解所得到的2014—2020年全国苹果价格季度均值的基尼系数值，以此来分析全国各省份的苹果价格地区差距，如图2所示，各地区苹果价格存在着较为明显的地区差距。首先，在2014年第一季度到2016年第二季度的地区差距呈现波动上升趋势，随后，2016年第三季度到2019年第一季度地区差距呈现波动下降趋势，从2019年第一季度到2019年第三季度地区差距持续升高，并且2019年第四季度地区差距达到阶段高点为0.46，之后到2020年第四季度地区差距降低并在0.4上下波动，但在此阶段地区差距仍然存在。

图2 2014—2020年全国苹果价格季度均值及地区差距Fig. 2 National apple price quarterly average and regional gap from 2014 to 2020

2.2 苹果价格的Granger因果关系

为分析山东省苹果价格波动因素，对山东与山东近邻省市之间的苹果价格空间传导效应进行分析，根据表1可得，山东、北京、江苏、河北4个城市苹果价格序列同阶单整，因此可进行Granger因果关系检验。设置VAR模型最大滞后期为4，如表2所示。根据VAR最优滞后阶数选取准则，选取最优滞后期为3，即传导周期为15 d。

根据Granger因果关系检验得知(见表3)，在1%显著性水平下，山东是引起北京、江苏和河北苹果价格变化的原因，并且存在北京与山东的双向Granger因果关系，山东多以传导源存在。各省苹果价格之间存在多个Granger因果关系，因此可以说明，苹果价格存在空间传导效应。

表1 各变量一阶差分的ADF检验结果Tab. 1 ADF test results of the first-order difference of each variable

表2 VAR最优滞后阶数确定Tab. 2 VAR optimal lag order is determined and established

表3 苹果价格Granger因果关系检验结果Tab. 3 Apple price Granger causality test results

2.3 苹果价格的动态演进

运用空间Markov链分析各地区苹果价格的空间动态演进，并对周边地区的苹果价格是否会影响本地区的苹果价格水平转移情况作出判断，基于表4所示的卡方检验的显著性检验结果，P值都小于0.01，当时长为1年(T1)、2年(T2)、3年(T3)、4年(T4)及5年(T5)后，Q统计值均在1%的水平下显著，表明空间因素对各地区苹果价格的转移产生显著影响。

表4 空间转移概率显著度结果Tab. 4 Significance result of spatial transition probability

表5揭示了空间因素对苹果价格的动态演进的影响，在地理权重下，以苹果价格高水平地区为例，当其相邻地区为高水平时，1年后该地区保持平稳转移概率为84%，5年后该地区保持平稳转移概率仍超过58%。

表5 苹果价格的空间Markov转移概率Tab. 5 Space Markov transition probability of apple price %

上述研究结果表明空间因素对苹果价格的影响较明显。在周围地区苹果价格较高的情况下，高水平地区降低自身苹果价格的难度较大，而与中、低水平地区为邻，促进本地区苹果价格的降低。此外，随时间推移，在不同水平“邻居”的影响下，苹果价格发生转移的概率总体上有所增加。

2.4 空间传导效应信息熵

利用熵值模型对价格空间传导多个特征进行信息熵拟合，包括基尼系数、Granger因果关系、以及空间Markov链系数，其中，因北京与山东存在双向Granger因果关系，熵值法中Granger因果关系值利用北京农产品市场富士苹果日均价格表示，得到如图3所示的信息熵序列。

图3 空间传导效应信息熵Fig. 3 Information entropy of spatial conduction effect

3 试验方案与结果分析

3.1 试验方案

1) LSTM模型。本文分别收集预测日的前25、50、100 d的苹果价格数据来预测价格，根据训练结果发现，选取50个苹果价格数据来预测下一日的价格预测效果较好，因此在后续试验中收集预测日的前50个数据进行试验。LSTM模型使用了五个隐藏层，其中，三个LSTM层以及两个全连接层，三个LSTM层的隐藏节点数分别为20、15和10，两个全连接层包含的隐藏节点数分别是5和1。为了防止过拟合，在三个LSTM层中加入了dropout函数，分别设置为0.3、0.8、0.8。本文将10%样本数据设为验证区间。

2) 加入信息熵。将空间效应的三项特征序列进行信息熵拟合，三项特征序列分别为基尼系数(GINI)、Granger因果关系、以及空间Markov链，将信息熵代替三项空间效应特征序列作为输入向量，结合LSTM对苹果价格进行预测。

3) 堆叠式LSTM。利用LSTM对空间传导特征提取后的信息熵进行预测，将预测的信息熵作为输入变量，并加入价格序列后利用LSTM模型预测苹果价格。利用LSTM预测信息熵后，再次结合LSTM进行预测的过程形成堆叠式LSTM(如图4)，对比LSTM与组合模型预测苹果价格的精度。

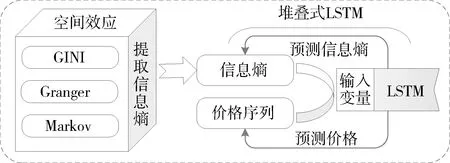
图4 堆叠式LSTM与熵值法组合预测流程Fig. 4 Stacked LSTM and entropy methodcombined forecasting process

4) 堆叠式多层LSTM。对神经网络的最优隐含层进行试验，得出预测苹果价格序列的最优神经网络层。

5) 模型预测性能对比。对比分析组合模型以及优化模型的预测性能。

本文使用均方误差(MSE)、平均绝对值误差(MAE)，与将两种误差通过异方差调整后的HMSE、HMAE，以上四种损失函数来评估模型的预测精度，如式(9)中所示。

(9)

RVt——真实值；

T——样本数量。

3.2 试验结果与分析

根据损失函数值评估模型预测性能，结果如表6所示。

1) LSTM模型。比较LSTM预测结果的损失函数发现，损失函数MAE为0.609 4，说明神经网络模型对苹果价格波动有良好的预测性能。

2) 加入信息熵。利用熵值模型对价格空间传导效应的三个特征项进行信息熵拟合，并结合LSTM进行预测，根据表6的预测结果发现，组合模型的预测性能优于LSTM模型，因捕捉到苹果价格的空间传导效应等特征信息，LSTM- 熵对比LSTM的损失函数HMAE从0.101 6降低到0.092 3，如图5所示三种模型部分预测值以及真实值的对比情况。

3) 堆叠式LSTM。堆叠式LSTM的预测损失函数MAE为0.508 7，在输入向量加入价格空间传导效应的基础上，改进的LSTM模型对苹果价格预测发挥了良好的作用。

4) 堆叠式多层LSTM。为寻找神经网络的最优隐含层，改变神经网络隐含层数对苹果价格序列进行预测，不同神经网络隐含层的预测结果的损失函数值如表7所示。针对苹果价格样本数据，在神经网络隐含层为4时，损失函数达到最低。

5) 模型预测性能对比。对比分析组合模型以及优化的组合模型的预测性能，加入价格空间传导效应的组合模型预测精度提高，利用堆叠式多层- 墒进行预测的损失函数比其他组合模型的损失函数低。以上结论证明，加入苹果价格的空间传导效应特征有助于提高预测精度，并且优化后的组合模型预测能力更强。

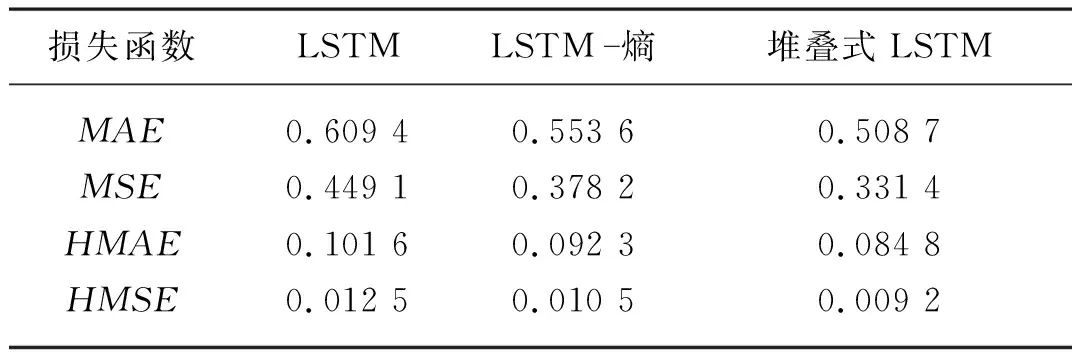
表6 模型损失函数比较Tab. 6 Model loss function comparison

图5 LSTM与组合模型预测结果截取Fig. 5 Prediction results snippet of single model andcombined model

表7 不同隐含层数损失函数对比Tab. 7 Comparison of loss functions withdifferent hidden layers

4 苹果价格预测分析

根据上述对苹果价格组合模型预测方法的研究，堆叠式多层LSTM与价格空间传导效应的熵值模型结合的组合模型预测精度较高。基于此，利用优化后的组合模型预测2021年1月1—31日的苹果价格，验证组合模型的预测能力。通过组合模型预测31 d苹果价格的损失函数MAE为0.448 8。从图6预测结果中可以发现，堆叠式多层LSTM- 墒组合模型预测数值在真实值附近波动，预测趋势与真实价格数据波动趋势相符，这进一步验证了基于堆叠式多层LSTM与熵值模型的组合模型对苹果价格预测的有效性。

图6 堆叠式多层LSTM-墒预测31 d苹果价格对比Fig. 6 Stacked multi-layer LSTM-E forecast31-day apple price comparison

5 结论

通过对苹果价格空间传导效应分析发现，苹果价格空间传导效应是引起苹果价格波动不可忽略的因素。利用基尼系数、Granger因果关系以及空间Markov链获取了苹果价格的地区差距、时空传导关系以及动态演进方向等多个价格空间传导特征，并利用熵值法客观提取多个特征的信息熵，结合改进的堆叠式多层LSTM模型的自身学习数据特征的特性，本文提出了一种堆叠式多层LSTM与熵值模型相结合的新方法。试验分析表明，(1)苹果价格存在较为明显的空间传导效应，各地区的苹果价格存在地区差距和Granger因果关系。(2)加入价格空间传导效应的堆叠式多层LSTM与熵值法相结合的组合模型预测精度提高，对比LSTM预测结果MAE的0.609 4，组合模型MAE为0.494 8，精度提高18.81%，在苹果价格预测方面发挥了良好的作用。

本文在现有价格预测基础上，增加输入向量，考虑价格空间传导效应特征，优化LSTM神经网络模型，进一步提高了价格的预测精度。由于价格数据受多种因素影响，如苹果的种植面积、国家政策、进出口贸易、苹果替代水果的价格变动等，众多因素共同对苹果价格波动产生影响，下一步的工作将增加影响因素的输入维度，进一步提高苹果价格预测精度，并增强预测模型的稳定性。