基于同源的旋转机械振源信号分离策略

贺志洋，刘东东，程卫东

(北京交通大学 机械与电子控制工程学院，北京 100044)

在工程应用中，采集到的信号包含多个激励源(振源)的振动。混合信号中用以表达机械状态的振源信号多被覆盖，难以提取到有效状态相关特征。从而不能准确表达机械设备的健康状态[1-2]。而清晰的故障振源信号有助于监测设备健康状态、分析结构特性、控制振动传递等。所以从混合信号中将能反映机械状态相关的振源信号分离出来是有必要的。

目前针对旋转机械的振源信号分离策略可总结为两大类：去噪模式的分离策略和盲源分离的策略。其中，去噪模式的分离策略在各行业中应用最广泛，它往往利用(时、频、时频)信号处理方法从混合信号中只分离出感兴趣的信号。由于它需要预先获取感兴趣信号或者噪声统计特征，因此又可分为两种：①已知感兴趣信号特征。何正嘉等[3]用时域平均提取了机床主轴的振动信号。Antoni等[4]首次提出谱峭度方法，用于混合信号中的冲击类振源与非冲击类振源分离。余建波等[5]提出了一种基于固有时间尺度分解与稀疏编码收缩集成的轴承故障特征提取方法，用于提取轴承的振动信号。②已知噪声特征。王天杨等[6]采用AR模型去除轴承故障信号中混入的齿轮啮合噪声，剩余信号则为轴承故障信号。彭玲[7]采用GVMD与流行学习方法对滚动轴承故障信号进行去噪，使得各故障特征频率的谱线显现出来。

盲源分离[8-9]的策略是从观测信号矢量出发，根据统计独立的分离或负熵最大化等准则搜寻分离矩阵，实现未知源信号矢量分离或恢复。无需传播通道信息以及源信号的先验知识就能求解分离矩阵的。近年来，盲源分离的相关理论应用于机械振源信号的分离。Ypma等[10]运用奇异值分解和双线性变换的方法进行了机械振动声源的盲分离与识别研究，并对工业泵的故障振源进行分离与识别。李志农等[11]利用局部均值分解(LMD)增维，解决了欠定盲源分离的问题，并且对轴承内外圈故障振源进行了分离。朱会杰等[12]利用移不变稀疏编码的盲源分离方法对轴承和齿轮故障的振源信号进行分离。

但是实际工程中振动激励源复杂，未确定机械运行状态时，并不能确定混合信号中振源信号或噪声的敏感统计指标，因此很难满足去噪类的分离策略的需求。盲源分离策略中存在如下不确定性：①其分离出来的信号幅值和相位不确定。②实际工程中振动激励源复杂，独立振源个数难以确定，目前均为估计和假设，会导致错分的情况；因此现有的振源信号分离策略主要存在振源信号特征不确定的问题从而影响振源信号的分离。

文中针对上述问题提出一种基于同源的故障振源信号分离策略。该策略建立待分离目标对象的描述，并将故障振源信号自身的性质作为分离的通用特征，克服了去噪类分离策略的未知振源信号的特征不确定性问题。该策略只分离与机械设备状态相关的振源信号，并非穷尽所有振源信号，故不需要预先确定振源数目。从而为振源信号的分离提供一个新思路。

1 基于同源的分离策略

基于同源的振动源分离的策略是根据机械(旋转及往复类)振源激发的响应(特征波形)具有同源性展开研究的。

1.1 同源响应的性质

文中将来自同一个振动源激发的每次振动称为同源响应。基于同源的分离策略是对其同源性质的应用。同源响应具有以下3个性质：

性质1：同源响应是由多次重复的响应片段组成。根据应用场景，旋转或往复式工作的机械，其上零部件的运动往往具有重复性。这个特点决定了单个激励的响应会多次重复出现。多次重复出现的响应片段串接组成了同源响应。同源响应可以看成多个小粒度的片段集合，可以在小粒度上寻找他们彼此之间的不同。

性质2：不同激励的响应片段形貌上存在差异，同源激励的多次响应片段具有相似的本质。机械零部件的材质和几何形态等物理信息不会在短时间内发生改变，每次激发的振动形态不会发生明显变化。

性质3：同源响应具有特定的、可计算的分布规律。由于旋转机械(或往复机械)的重复特性、固定的传动结构和运行转速(或往复周期)，振动源激发振动的频次也满足特定的规律。不同的激励响应具有不同的分布规律。

1.2 分离策略

基于同源的振源信号分离策略利用同源响应的三个性质，从混合信号中依次分离出与机械设备状态相关的振源信号，直到不能分离出为止。该策略主要分为两部分：第一，从待分离信号中确定振源；第二，分离振源信号。分离策略及步骤如图1所示。

图1 分离策略示意图Fig.1 Schematic diagram of separation strategy

第一部分中，从待分离信号中找到一个振源信号是指确定存在的振源和其所有响应片段的位置。首先可根据模式相似性质从混合信号中找到一个振源的两个或若干响应片段。再根据这些活跃响应片段的位置计算出其频次(分布规律)。通过分布频次可计算出其它所有响应片段的位置。

能够从混合信号中找到一个振源的两个或若干响应片段是因为振源信号具有稀疏性。即该振源信号与干扰在某一个域(时域、频域或者第三个域)中是不重叠的。

如时域稀疏，设一个振源激发的特征波形为s，X为观测信号，X=[x1,x2,…,xN]，n为干扰信号，其中n包含其它振源的信号和环境噪声等，则该振源的特征波形的观测信号为如下式所示。

(1)

由于振源的响应和干扰在混合信号中存在交替交错排列，则干扰n中的某几个干扰成分趋近于0的，即此时信号中只有一个振源的信号起主导作用，Georgiev等[13-14]将其称为活跃片段。若ni趋近于0，则xi是活跃片段。

正是因为一个振源的活跃片段被其它振动干扰微弱，故可根据同源响应片段的模式相似性直接挖掘到混合信号中的活跃片段及其位置。

可从一个简单的例子观察到时域稀疏源的混合信号中存在活跃状态片段。如图2所示，源1和源2为时域稀疏的源，观测信号即为两源的混合信号。左侧框内的混合信号为源1活跃状态片段，右侧框内的混合信号为源2活跃状态片段。

图2 混合信号中存在活跃状态片段Fig.2 Active state fragments in mixed signals

当然并非所有的源信号都满足时域稀疏。针对这个问题，Bofill等[15]提出可通过一些域的变换方法将在时域不稀疏的信号在其它域(如频域、时频域等)转变为稀疏，因此可在其它域找到活跃状态片段。

第二部分中，将振源信号从混合信号中提取出来的本质是将多个响应片段放在一起关联分析，通过提取或者构建其共有成分实现振源模式的恢复和振源信号的提取。该部分是根据同源响应具有模式相似的性质，将受到不同程度的污染的同源响应片段还原的过程。

其中，关联方式提取信息早在图像处理中就得到了应用，即将多个样本同时分析，相互增强，恢复样本的真实信息。在图像处理中，现有的关联方式主要有基于鲁棒特征的方式和机器学习的方式等。鲁棒特征的方式首先将图像分解成为多个子图。Gao等[16]通过对多个图像样本计算相似来判断子图属于干扰子图和正常子图，满足相似则为正常子图(即鲁棒特征)。其鲁棒特征也是样本的共有特征。机器学习的方式则是将多个样本送入同一个学习模型(如支持向量机、深度学习等方法)[17-18]，每次迭代和更新权值实现在大量不同部位不遮挡的样本中提取到真实特征。学习到的特征是样本的共有特征。如来自UMIST数据库的人脸样本，每个人从侧面到正面的图片都是在一系列不同的姿态中拍摄的，如图3所示。针对该类问题，不可能从一个样本中得到全部的人脸信息。在图3的a1～a7中，a2、a3、a5的耳朵被遮挡，其余4张图像中耳朵部位未被遮挡。那么在训练的过程中，多次迭代从a1、a4、a6、a7中得到耳朵的信息，实现信息互补。再如图3的b1～b7中，b1和b3的嘴部受到不同程度遮挡，但在学习中也可通过其它图像得到嘴部信息。所以可通过样本之间的相互关联，使信息得到补充，得到真实的图像，如图3中a8和b8。这也从另一方面为通过共有成分重构恢复振源信号提供了理论支持。

图3 来自UMIST数据库被随机遮挡的人脸图像Fig.3 Face images from the UMIST database that were randomly blocked

1.3 分离对象

安装在旋转或往复机械系统上的振动传感器所测得的振动信号是多激励源激发振动的混合，如图4所示。基于同源的振源信号分离并不是将一个混合信号中的全部振源的信号分离出来，而是只分离与机械设备状态相关振源的信号。且不可能得知一台机械全部振动激励源的种类，以及每种激励源的数量。且分离与机械设备自身状态无关的激励源信号是无意义的。

许多专家学者对机械设备异常状态激励源的振动展开了研究。屈梁生等[19-20]研究了转子系统故障，指出转子不对中导致出现离心力，从而使转子激发出二倍及高倍频的谐波类振动；徐敏等[21]对滚动轴承故障做了系统研究，指出轴承裂纹故障是由滚动体与裂纹处发生碰撞产生冲击力，由此激发出一个个脉冲，表现为衰减振荡波形；Sfakiotakis[22]、James Li[23]和MackAldener[24]对齿轮振动进行了研究。他们指出齿轮齿面磨损时，其振动信号时域波形偏离正弦波，并且磨损越严重，波形越接近方波；齿轮断齿时由于齿轮的碰撞，会激起齿轮与箱体的固有频率，并且在时域波形中表现为以齿轮转频为周一的冲击现象。

因此根据激励随时间变换规律可将反映旋转或往复机械健康状态的振源信号分为三类：简谐激励、冲击激励和任意激励产生的响应。

这三类振源的响应均为逐次激发，在信号中是一个个响应片段串接而成，因此具有片段串连性。其次，这三类振源均具响应的分布有一定的周期或者与转速成比例，因此具有特定的分布规律。且这三类振源的激励条件短时间内未发生变化，因此响应片段具有相似的本质。所以该三类振源的响应片段满足同源响应的三个性质。而其它振动及干扰种类繁多，具有随机性和间歇性。因此它们并不具有一定的分布规律和相似的模式特征等，即不具有同源响应的性质。所以三类振源既是与机械设备状态相关的振源，恰好也是满足基于同源的振源分离的对象。

2 一种基于同源分离策略的振源分离方法

基于同源的分离策略框架下的振源分离方法主要包含振源确定和振源信号分离两部分。

首先，振源确定。文中采用MP(matrix profile)方法[25]与同源响应片段特征寻找混合信号中最具有同源模式的活跃响应片段对。该特征分为两点：①模式特征，这里表现为时间序列中同源响应片段的相似特征；②分布规律，是指同源响应片段间隔的分布距离符合L=nT，其中n∈N+，T为故障响应周期。其中根据MP算法寻找到的最相似片段对的分布距离是否满足某个振源分布规律，来判定是否为待检测振源信号，且可计算的到其它响应片段位置。振源确定方法的流程如图5所示。

图5 振源确定方法流程图Fig.5 Flow chart of vibration source determination method

其次，共有成分重构的方式分离振源信号。将每个振源响应片段分解为多个子成分，根据同源响应片段模式相似的特征，通过相似检测提取多响应片段中相似成分，并重构。其方法示意图如图6所示。

图6 基于共有成分重构的振源信号提取方法Fig.6 Vibration source signal extraction method based on common component reconstruction

其中，振源响应片段的分解过程中可直接借助现有的信号分解方法，如共振稀疏分解、小波分解、奇异谱分析等。分解方法的选择需要满足待分离振源与其余信号在该分解方法的表达域(如时域、频域、品质因子等)下不混叠。

将其子成分分为两类：共有成分和非共有成分。响应片段分别用A1,A2,…,Am表示，Aij是Ai经过分解的第j个成分。

按照对应成分两两计算相似度，每一成分均会得到一个相似度三角矩阵

(2)

式中，Similarityj为第j个成分的相似三角矩阵，如A1jA2j表示第A1j个成分和第A2j成分的余弦相似值。

其次，文中通过某一序号成分相似度的平均值来衡量该成分是否为共有成分。只要选择合适的相似度阈值T即可确定两个成分是否为共有成分。所以判定成分j是否为共有成分，可根据SIM_MEANj是否大于T来判断

(3)

这样就可以判断出Y个成分是否为共有成分。其中T取值太大会提取不到共有成分，取值太小则提纯效果差，故设置合适的T很重要。文中通过o’tsu自动阈值法确定划分共有与非共有成分的阈值。

响应重构是把标定为共有成分的各响应子成分重构回原响应。响应重构式如下

(4)

SIM_mean=[SIM_mean1,SIM_mean2,…,SIM_meanL]

(5)

其中AR1，AR2，…，ARm分别为第1，2，…，m个重构响应。

3 基于同源分离策略的应用案例

3.1 轴承内外圈故障振源的分离

以滚动轴承内圈和外圈故障振源混合的信号作为分析对象。数据来源美国凯斯西储大学公开数据，测试轴承为支承电机驱动轴的深沟球轴承，轴承型号为62205-2RS JEM SKF，参数如表1所示。使用电火花技术加工一个损伤直径为0.018 cm的外圈故障轴承，一个损伤直径为0.018 cm的内圈故障轴承，转速为1 796 r/min。加速度传感器安放在电机壳体的驱动端位置采集振动数据，采样频率fs=48 kHz。

表1 驱动端6205-2RS JEM SKF轴承结构参数Tab.1 Driving end 6205-2RS JEM SKF bearing structure parameter

图7 MP搜索混合信号中最相似的活跃状态响应片段Fig.7 MP searches for the most similar active state response fragments in the mixed signal

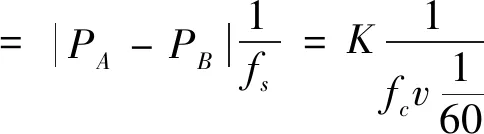
(6)

(7)

式中：fc为某一振源的分布规律；V为转速。经计算，当fc=Co时(对应外圈故障振源)，K为3.98，最接近正整数4。出现该情况是因为滚动轴承的滚子在运动过程中有1%～2%的滑移误差，且误差随着响应片段间隔时间的增加而累加。故可判定该活跃片段为外圈故障引起的响应片段。因此可以在存在内圈故障振源的干扰情况下找到外圈故障振源的。进一步，根据外圈故障振源的分布规律，计算出混合信号中外圈故障响应片段的全部位置。

虽然混合信号中的振源频带重叠，但是其振荡的能量不同，故具有不同的品质因子。共振稀疏分解方法按信号的共振属性将信号分解为具有持续振荡的高共振分量和没有持续振荡的低共振分量。故选定共振稀疏分解为信号的分解方法。通过对外圈故障振源的响应片段进行共有成分重构，得到其信号如图8(a)所示。从图8(b)中可以看出其故障特征频率(107.3 Hz)处出现明显峰值。

图8 外圈故障振源的分离波形及其包络谱Fig.8 Separate waveform and envelope spectrum of faulty vibration source of outer ring

同样，根据振源确定方法，对残差信号查找活跃片段对，根据MP找到的motif位置为第1和8 019个采样位置，如图9所示。根据式(1)计算其分布规律为5.99 Hz，当fc=Ci时(对应内圈故障振源)，经计算K为27.08，最接近整数27。考虑滑移误差，可判断该次找到的活跃片段对为内圈故障响应片段。再根据fc计算出其余响应片段的分布位置。

图9 内圈故障振源活跃片段Fig.9 Active segments of inner ring fault vibration source

通过对内故障振源的响应片段进行共有成分重构，得到其信号如图10所示。其内圈故障特征频率在162.2 Hz处呈现较大峰值。

图10 内圈故障振源的分离波形及其包络谱Fig.10 Separate waveform and envelope spectrum of inner ring fault vibration source

3.2 齿轮啮合与轴承外圈故障振源的分离

齿轮啮合与轴承外圈裂纹故障振源分离的试验数据是利用机械故障试验台(MFS)获得，如图11所示。故障轴承安装在靠近电机侧，振动传感器安装于故障轴承座上。采集系主要有DAQ采集卡(NI-PCI6259)和NI-DAQmx采集软件组成。故障轴承主要参数及试验台主要参数如表2所示。

图11 MFS试验台Fig.11 MFS test stand

表2 故障轴承及FMS试验台主要参数Tab.2 Main parameters of faulty bearing and FMS test stand

测取的齿轮啮合与滚动轴承裂纹故障振源的信号如图12所示，采样频率为48 kHz，通过MP对该时域信号查找其活跃片段，其位置为第5 752和8 507个采样点。经计算，当fc=3.052时(对应外圈故障振源)，其分布规律为17.42 Hz。K为6.05，最接近正整数6。考虑其滑移误差，可判定为该活跃片段为轴承外圈故障引起的响应片段。进一步，根据其外圈故障振源的分布规律，计算出混合信号中外圈故障响应片段的全部位置。

图12 实测信号时域波形Fig.12 Time-domain waveform of measured signal

因为从混合信号中可以看出其包含谐波和冲击类成分，其在频域中振源信号间具有良好的稀疏性。所以响应片段的分解方法选择为小波包分解，其中小波包分解层数为3。得到各需片段子分量，根据共有成分的判定方法对振源响应片段做重构。即可得到轴承外圈故障振源信号，如图13(a)所示。从其对应的包络谱图13(b)中可以看出，其故障特征频率105 Hz处出现明显峰值。

图13 内圈故障振源的分离波形及其包络谱Fig.13 Separate waveform and envelope spectrum of inner ring fault vibration source

重复分离步骤中的1、2步，得到齿轮啮合振源信号，如图14(a)所示。其频谱如图14(b)所示，其齿轮啮合频率398 Hz附近处出现明显峰值。

图14 齿轮啮合振源的分离波形及其频谱Fig.14 Separation waveform and frequency spectrum of gear meshing vibration source

从上述两个试验案例可以看出，基于同源响应的振源分离策略可有效分离旋转机械设备的振源。

4 结 论

(1)针对现有振源信号分离策略中振源信号特征和振源数目等难以确定的问题，提出一种振源的分离策略。归纳了与旋转机械健康状态相关的振源信号的三个性质(即为同源性质)，并将振源信号的同源性质作为分离准则。该准则不需要提前获得内激励响应的相关特征，具有通用性。通过试验分析证明该分离策略的可行性。

(2)在判定是否为共有成分时，基于该策略给出的分离方法过分依赖于相似度计算。当同源响应的相似度较低时，会导致分离效果变差。