正态分布概率区间模糊数及测度问题①

丁润霞, 黄韩亮

(闽南师范大学数学与统计学院, 福建 漳州 363000)

0 引 言

由于模糊集在处理不确定信息方面是目前学术界最有力的工具, 自Zadeh提出模糊集[1]以来, 模糊集理论及其衍生概念被广泛运用于决策[2],[3]、规划[4]、控制[5]、推理[6]、模式识别[7]等领域.1987年Gorzaczany提出区间模糊集[8]的概念, 他在模糊集基础上将隶属度从一个数扩展到了一个区间上, 减少了数据信息的丢失, 为决策者提供了更大的决策空间.区间模糊集是指元素对模糊集的隶属度为一个区间, 即元素在隶属度区间上概率相等.但在专家给出偏好信息时, 元素在隶属度区间上的概率往往不相等, 因此研究隶属度在区间上的概率分布具有实际意义.正态分布在计算机、医学、经济学领域是一种重要的概率模型, 如预测算法、质量控制、岗位预测等实际问题均可用正态分布来描述.所以考虑模糊元素在隶属度区间上概率呈正态分布的情形, 创造性地提出了正态分布概率区间模糊集和正态分布概率区间模糊数的概念.正态分布概率区间模糊集是指模糊元素在隶属度区间上的概率分布为正态分布的情形.为了进一步研究正态分布概率区间模糊数的性质, 提出了正态分布概率区间模糊数的相似测度和距离测度.通过这两类测度可以将正态分布概率区间模糊数之间的关系进行量化.

1 预备知识

定义1[1]设U为论域, 则U上的一个模糊集合A由U上的一个实值函数

来表示.对于x∈U, 函数值μA(x)称为x对于A的隶属度, 而函数μA称为A的隶属函数.

则

(1)A1∪A2=

(2)A1∩A2=

2 正态分布概率区间模糊集

现有的关于区间模糊集的研究, 是用一个精确的隶属度区间来描述元素对模糊集合的隶属程度, 即在这个区间上每个点的概率是一样的.但随着社会的发展, 决策信息越来越复杂, 隶属度在区间上每个点的可能性往往不相等.正态分布是统计学中一个十分重要的概率分布, 所以本文考虑模糊元素在隶属度区间上的概率分布为正态分布这一连续型概率的情况, 提出了正态分布概率区间模糊集和正态分布概率区间模糊数, 即隶属度区间上的概率分布为正态分布的情形, 增加了评价者的评价空间.接下来给出正态分布概率区间模糊集和正态分布概率区间模糊数的定义

图1 正态分布概率区间模糊集A={a,b,c}的图像

图2 正态分布概率区间模糊数α的图像

对于正态分布概率区间模糊数我们定义它的并、交、补运算如下:

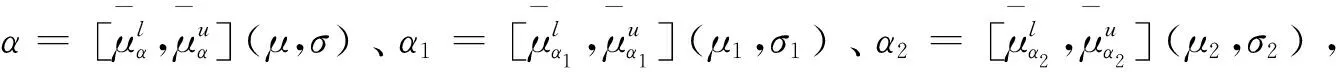
(2)α1∪α2=

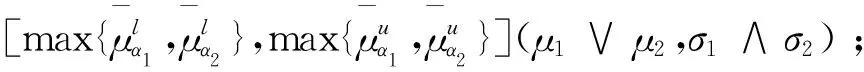
(3)α1∩α2=

基于以上的运算法则, 有下面的运算性质:

(1)幂等律:α∪α=α;α∩α=α;

(2)交换律:α1∪α2=α2∪α1;α1∩α2=α2∩α1;

(3)结合律:(α1∪α2)∪α3=α1∪(α2∪α3);

(α1∩α2)∩α3=α1∩(α2∩α3);

(4)吸收律:(α1∪α2)∩α2=α2;

(α1∩α2)∪α2=α2;

(5)分配律:α1∩(α2∪α3)=(α1∩α2)∪(α1∩α3);α1∪(α2∩α3)=(α1∪α2)∩(α1∪α3);

(6)复原律:(αc)c=α.

证明:由定义5易知(1),(2)显然成立, 下证(3),(4),(5),(6).

=

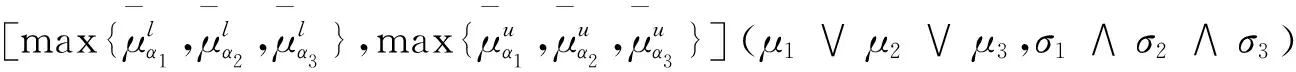
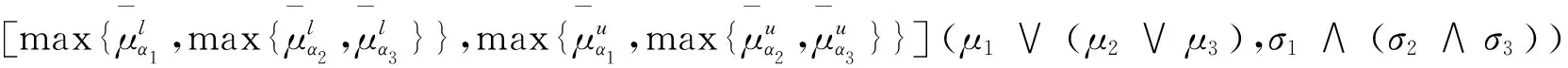
同理可得(α1∩α2)∩α3=α1∩(α2∩α3).

=

同理可证(α1∩α2)∪α2=α2.

(5)由定义5知

=

因为

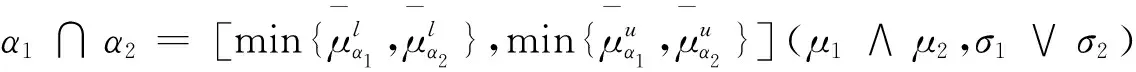
可得

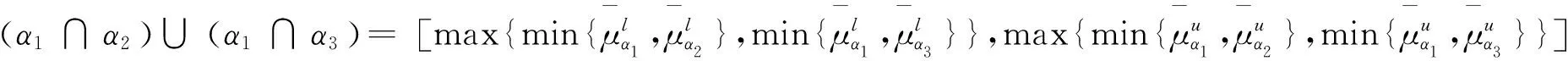
((μ1∧μ2)∨(μ1∧μ3),(σ1∨σ2)∧(σ1∨σ3))

又因为

(μ1∧(μ2∨μ3))=((μ1∧μ2)∨(μ1∧μ3))

σ1∨(σ2∧σ3)=((σ1∨σ2)∧(σ1∨σ3))

故

α1∩(α2∪α3)=(α1∩α2)∪(α1∩α3);

同理

α1∪(α2∩α3)=(α1∪α2)∩(α1∪α3).

3 正态分布概率区间模糊数的测度问题

相似测度、距离测度是模糊集理论的重要研究内容, 国内外专家学者对此十分重视.为研究正态分布概率区间模糊数之间的关系, 根据其特点构造正态分布概率区间模糊数的两种测度如下:

定义6设有两个正态分布概率区间模糊数

则

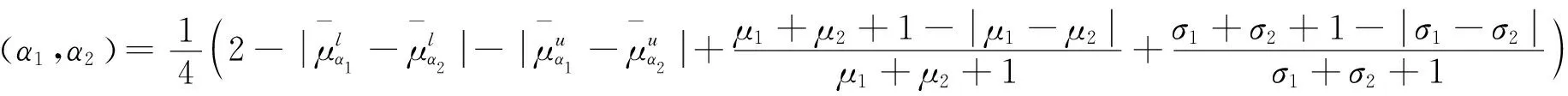
定理2相似度ϑ(α1,α2)满足下列性质

(1)0≤ϑ(α1,α2)≤1;

(2)α1=α2⟹ϑ(α1,α2)=1;

(3)ϑ(α1,α2)=ϑ(α2,α1).

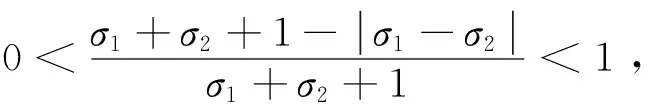
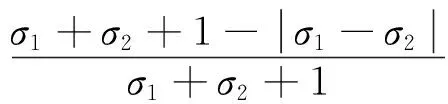
综上所述

0≤ϑ(α1,α2)=

(2)当α1=α2时, 即

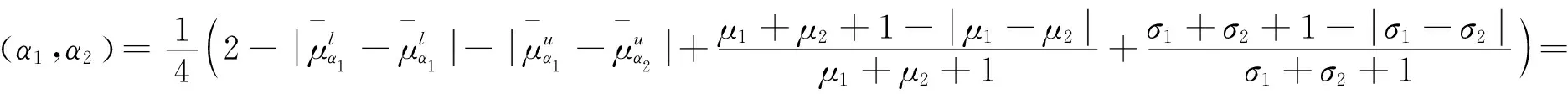
(3)ϑ(α1,α2)=

ϑ(A2,A1).

定义7设有两个正态分布概率区间模糊数

则

d(α1,α2)=1-ϑ(α1,α2)=

称d(α1,α2)为α1和α2的距离测度.

定理3距离测度d(α1,α2)满足下列性质

(1)0≤d(α1,α2)<1;

(2)α1=α2⟹d(α1,α2)=0;

(3)d(α1,α2)=d(α2,α1).

证明由定理2易知.

例1在正态分布概率区间模糊集

A={a=[0.4,0.7](0.5,0.2),

b=[0.4,0.7](0.6,0.2)，

c=[0.4,0.7](0.6,0.5)，

d=[0.4,0.5](0.5,0.7)}

中找一个与e=[0.4,0.8](0.5,0.2)最相似的正态分布概率区间模糊数.

首先计算正态分布概率区间模糊集A中每一个元素与d的相似度

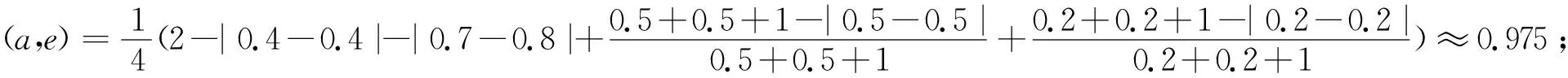
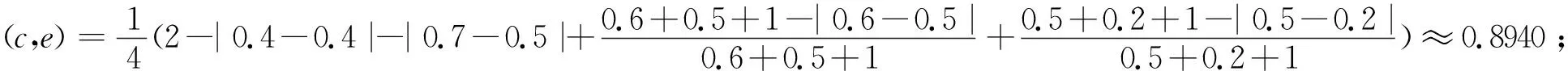
综上所述a与e的相似度最大为0.975, 其次是b与e为0.9631, 接着是c与e为0.8940.观察数据发现a与e只在隶属度区间上不同, 而b与e的隶属度区间和期望都不同,c与e的隶属度区间、期望、方差都不相同, 故较a,b来说c与e相似度更小.d与e和a与e相比隶属度、方差相差更大, 故较a来说,d与e相似度更小, 符合现实规律.

4 结 语

本文定义了正态分布概率区间模糊集、正态分布概率区间模糊数, 并给出了正态分布概率区间模糊数的运算, 且运算满足许多优良性质, 与自然规律相符, 说明了运算是优良的.接着给出正态分布概率区间模糊数的相似测度、距离测度来量化正态分布概率区间模糊数之间的关系.