全钢双矩管防屈曲支撑在不同间隙下的受力性能研究①

李浩宇, 岳鹏飞

(1.安徽大学艺术学院,安徽 合肥 230601;2.安徽省交通控股集团,安徽 合肥 230031)

0 引 言

防屈曲支撑由外部约束构件包裹内部构件形成受力时屈服而不屈曲的轴心受力构件[2]，支撑整体具备良好的侧向刚度和承载能力，目前工程实际中多采用从日本、美国进口[3]的钢管混凝土组合支撑，该类防屈曲支撑自重大、制作成本高且不便于施工组装，自重较大会加大地震作用，加速支撑和整体结构的损坏。近年来，由于装配式建筑和绿色建筑的迅速兴起，对构件轻量化的要求日益提高，国内外出现了大量全钢防屈曲支撑，但其外围约束构件多采用格构式截面[4-6]，导致其制作和加工成本较高，难以广泛应用于工程实际中，与之不同的是，Jay Shen[1]等人提出一种内外钢管均为型钢的全钢防屈曲支撑，通过防屈曲支撑内管的弹塑性变形进行耗能,对该类全钢防屈曲支撑进行了大量的试验和理论研究，研究结果表明内外钢管间的间隙大小是影响支撑滞回性能的重要因素，内外钢管管壁厚度比值控制在1时有较好的约束性能[7-8]。文中将支撑内管由圆管替换成方管，方管的平面外刚度较圆管更大，同时在运输和装配过程中不易变形，也是将其用于防屈曲支撑内管的原因之一。对TinT支撑受力性能进行数字模拟和分析，并与试验结果进行比较。首先研究了初始缺陷大小对支撑的影响以真实的模拟支撑缺陷，其次以内外管间不同间隙大小为主要研究对象，建立精细的实体单元模型进行拉压往复荷载下的有限元数值分析，分析不同间隙大小对支撑滞回性能和承载能力限值的影响，考察相比于传统支撑受力性能和耗能性能的改善，并将数值模拟结果与试验现象比较。

1 支撑构件设计与有限元分析

1.1 支撑组成与作用

双矩管全钢防屈曲支撑尺寸如图1-3所示，支撑由内外两个全钢方管及焊接于内管两端的加劲肋版组成，组成及网格划分如图4所示，双矩管全钢防屈曲支撑采用矩形型钢管套装而成，为避免内管端部薄弱处过早屈服，在内管管壁两侧开槽焊接加劲板增强端部抗弯强度，考虑到实际需求，将防屈曲支撑两端设计为铰接或者刚性连接[5]，当支撑绕弱轴y轴屈曲时，相比其他全钢屈曲支撑未见明显区别，当支撑绕x轴屈曲时，由于矩形截面较大的惯性矩和平面内抗弯刚度，提高了绕x轴承载力。

图1 支撑整体示意图

图2 支撑内管截面示意图

图3 支撑外管截面示意图

图4 TinT支撑组成及有限元网格划分

1.2 有限元模型

有限元尺寸如表1所示，运用布尔运算方法划分各组成构件网格，采用8mmC3D8R实体单元[6]，沿壁厚方向有三个网格。为模拟工程实际，将支撑外管 相对于内管设为固定连接，并将内管设为一端固定一端铰接的约束形式，以实现内核钢管和加劲肋板的挠曲变形协调，为避免模拟中各构件间出现相对z轴的错动，取内管、加劲板为一个整体构件，外管作为一个独立构件。内外管间接触形式为面面接触，摩擦系数设定为0.3[6]，不考虑内外管壁沿z轴方向的摩擦。

表1 内外管不同间隙的有限元模型

依据《金属材料拉伸试验 第一部分室温试验方

(GB/T228.1)[7]选用同等厚度的钢材进行材料拉伸试验，每组取三个试验结果平均值作为材料最终实验数据，计算得钢材屈服强度fy，弹性模量E、屈强比fy/fu、抗拉强度fu、伸长率，结果如表2所示。支撑钢材fy=345MPa，E=2.06×105Pa，强化Est=0.032×E=6592MPa，材料参数选取表2中数据。

表2 支撑材料力学性能汇总

1.3 支撑极限承载力

在支撑端部施加单向递增(压力)位移荷载，加载制度如图5所示，直至加载到2%SDR[1](层间位移角缩写SDR)位移大小，图6为各支撑的荷载-位移曲线，横坐标为内管轴向位移数值，纵坐标为支撑承载力Fpyc和内管屈服荷载Fy之比。

图5 单向递增位移荷载(压力)

结合表3和图6可知，传统tube支撑在0.55SDR时，Fpyc/Fy即出现下降，承载力限值数值低下，TinT-1、TinT-2、TinT-3支撑由于外管约束，未在2%SDR位移荷载前出现承载力下降；TinT-4、TinT-5支撑在1%SDR时，Fpyc/Fy出现下降，由于支撑端部形成塑性铰导致整体失稳破坏。

表3 各支撑Fpyc/Fy下降值

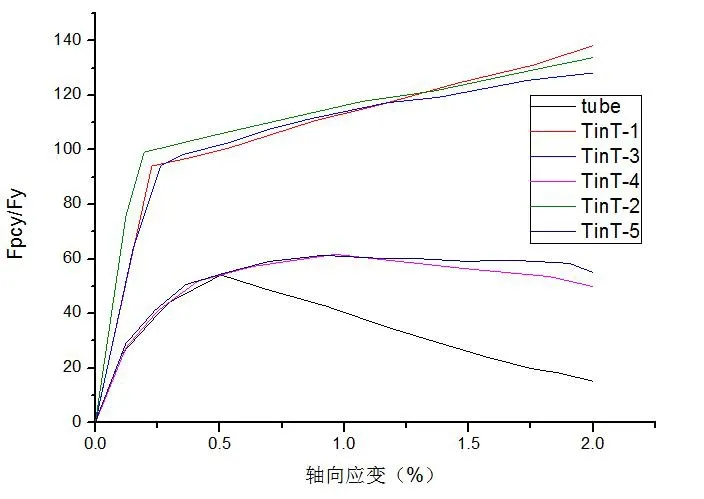
图6 Fpyc/Fy-位移曲线图

2 支撑的滞回性能与耗能能力

2.1 传统支撑与防屈曲支撑滞回性能比较

(1)对Tube支撑施加往复位移荷载，如图7所示，支撑变形如图9所示，Tube支撑跨中部位形成塑性铰，并出现整体失稳破坏，模拟结果与文献[1]中试验结果高度相似,如图8所示。

图7 位移荷载曲线

(a)文献[1]中传统支撑滞回曲线

图9 传统支撑有限元模拟结果

(2)取TinT-2支撑为研究对象，施加图7位移荷载，支撑在轴力作用下绕x轴弯曲，内管伸出外管部分缺乏约束，形成塑性铰产生破坏，比较文献[1]试验结果(见图10所示)可知，防屈曲支撑在端部加劲板部位形成塑性铰导致破坏，与文献中试验结果较为一致。

图10 TinT支撑模拟与文献[1]试验结果比较

传统支撑和防屈曲全钢支撑的受力性能比较如表3所示，TinT-2支撑的抗震耗能性能和滞回性能得到有效改善和提高。

表3 传统支撑和防屈曲支撑的性能比较

2.2 不同间隙支撑滞回性能与耗能性能

2.2.1 初始缺陷对防屈曲支撑滞回耗能性能的影响

由于生产工艺限制，预制型钢管构件均存在几何缺陷，为研究内管初始缺陷大小对支撑受力性能的影响，假定外管为无几何缺陷的完善构件，内外管间隙为2mm,为保证支撑内外管在加载初期产生接触，避免外管刚体位移，及可能的计算模型不收敛问题，分别对内管施加幅值为1mm、2mm的初始缺陷[8]，综合比对无初始缺陷内管的防屈曲支撑受力性能，分析结果如图11所示。

图11 初始缺陷对TinT支撑受力性能的影响

由图11可知，支撑初始缺陷为1mm、2mm时，受力性能无明显差别，对比无初始缺陷时屈服荷载分别下降10%和15%.

由图12可知，在不同初始缺陷大小下，支撑外管对受力内管的约束基本维持不变，均呈现出三波段的应力图形，主要由于支撑端部处弯矩较大，产生较大剪力，导致内管管壁间应力增加，跨中形成塑性铰，导致支撑外管在跨中部位受力较大。

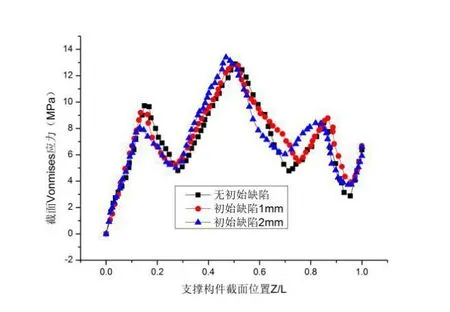
图12 不同初始缺陷大小下外管应力分布

综合分析防屈曲支撑取1mm与2mm大小的初始缺陷对支撑受力性能影响差别不明显。

2.2.2 滞回耗能性能分析

为了更好的分析支撑的滞回性能和耗能性能，在支撑端部施加轴向拉压往复位移荷载(图7所示)，计算能量耗散系数E、等效粘滞阻尼系数ξe、按式(1)、(2)计算[9]，式中各参数如图13所示，计算支撑的总耗能及滞回曲线ξe、E，如表 4所示。

图13 等效阻尼比参数取值示意图

表4 各支撑滞回性能与耗能性能指标

(1)

E=2πξe

(2)

图14 5mm间隙下的支撑应力分布

图15 5mm间隙下的支撑滞回曲线

图16 4mm间隙下的支撑应力分布

图17 4mm间隙下的支撑滞回曲线

比对分析各支撑数字模拟结果(如图14-23所示)，可将其概括为三类。第一类，支撑滞回曲线出现捏拢现象，整体应力承载力低下，如Tube支撑。第二类，该类支撑能够完成1.667%SDR的滞回位移荷载但不能完成2%SDR滞回位移，滞回曲线相对饱满对称，可作为有一定耗能能力的承载型支撑使用，也可作为增强抗侧刚度的支撑使用，如TinT-5、TinT-4、TinT-3支撑[10]。第三类，支撑具备累积塑性应变要求，能很好的完成2%SDR的滞回位移荷载，可作耗能支撑使用，如TinT-2、TinT-1支撑。以TinT-2 为例，因外管提供约束，支撑整体未见屈服现象；TinT-2支撑在1.667%SDR的第三次受压位移荷载时，内管截面出现屈服变形，支撑整体能够完成2%SDR位移荷载，但支撑端部肋板处形成塑性铰失稳破坏；TinT-1支撑在1%SDR位移荷载时，内管局部产生屈服变形，内外管间隙过小导致内外管间互相干扰，支撑外管参与轴向受力，整体受力性能下降。综上所述，当间隙δ>3mm时，TinT支撑能够达到1.677%SDR轴向位移，可作为承载型防屈曲支撑使用。当δ<1mm时，TinT不可作为耗能支撑。1mm<δ<2mm，TinT支撑可作为耗能性型支撑使用。

图18 3mm间隙下的支撑应力分布

图19 3mm间隙下的支撑滞回曲

3 结 论

为了适应国家提出的装配式建筑理念和工程实际中承载耗能需求，提出全钢双矩管TinT防屈曲支撑并对支撑的单调承载力、反复拉压滞回性能和耗能能力进行了研究，对文中研究尺寸的全钢防屈曲支撑主要有以下两个方面结论：

1)首先比较了防屈曲支撑和传统支撑静力轴向受压单调加载承载力，结果表明，防屈曲支撑相对传统支撑最大受压承载力提高约100%，支撑破坏形式主要有三种模式:Tube支撑内管未达到全截面屈服就发生整体失稳破坏；部分支撑轴向位移未达到2%SDR时，如TinT-4、TinT-5支撑内管已经进入全截面屈服且在端部形成塑性铰产生整体破坏；当支撑间隙δ<3mm，内管全截面屈服且轴向应变达到或超过2%SDR而不破坏。

图20 2mm间隙下的支撑应力分布

图21 2mm间隙下的支撑滞回曲线

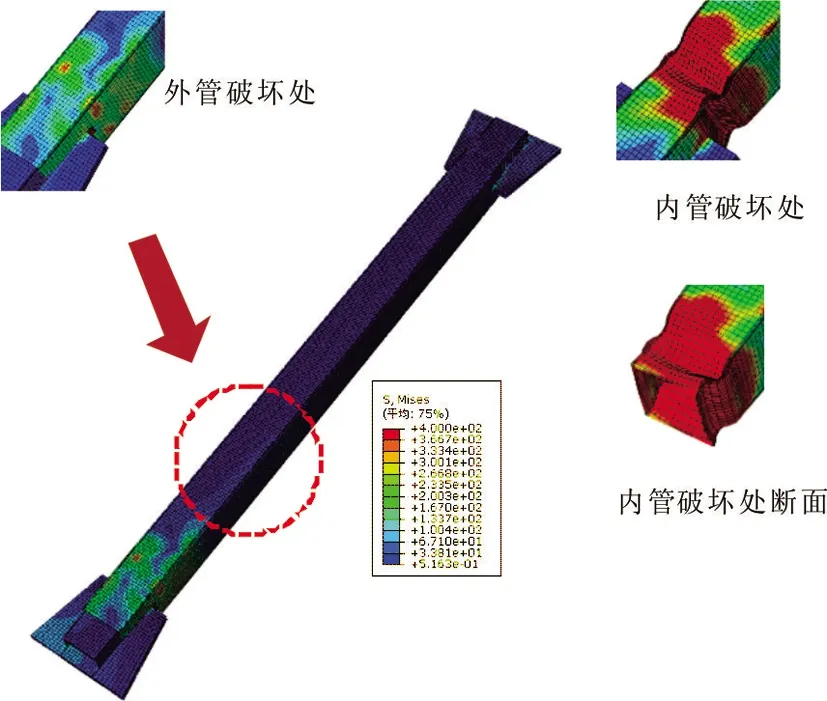
图22 1mm间隙下的支撑应力分布

图23 1mm间隙下的支撑滞回曲线

2)研究支撑往复位移荷载下的承载能力和滞回耗能性能，分析不同大小的初始缺陷对支撑滞回受力性能的影响，研究分析表明，初始缺陷大小对支撑受力性能影响较小，取值在1‰～l之内时，均可较好的模拟支撑真实受力情况，其次分析间隙大小对支撑滞回受力的影响，Tube支撑滞回曲线紧缩捏拢严重，滞回耗能性能低下；当3mm<δ时，该类支撑可作为结构整体承载力提高构件使用，但不具备耗能支撑2%SDR累积塑性变形指标，当1mm<δ<2mm，支撑具备2%SDR累积轴向塑性变形能力，最终于支撑端部形成塑性铰破坏，该类支撑可作为滞回耗能型支撑使用。