面向医疗数据可信共享的映射泛化(k,l)-匿名算法

康海燕，邓 婕

(1.北京信息科技大学 信息管理学院，北京 100192；2.北京信息科技大学 计算机学院，北京 100101)

0 引言

电子病历(electronic medical record,EMR)中包含有病人各种敏感数据，如姓名、住址、联系方式、检查记录、疾病诊断甚至是家族遗传史等，这些敏感数据一旦被篡改或被泄露，有可能使个体遭受社会的负面评价，甚至歧视或者侮辱，影响个体的生活或者心理状态[1-3]。因此，当医疗机构或病人对外共享数据时，如何在保护隐私安全的前提下保证数据的真实可用性，成为医疗信息领域的一个热点问题。

Samarati等[4]为了解决数据库和数据发布的应用问题首次提出匿名的概念。该算法的主要思想是让数据集中的准标识符属性拥有相同的取值，以达到不怀好意者无法确定敏感属性所属主体的目的，从而保护个人隐私不被泄露。Sweeney等[5]把该模型命名为k-匿名隐私保护模型。之后陆续有学者针对k-匿名模型存在的缺陷，提出了很多改进的匿名模型。例如，Gehrke等[6]提出了l-多样性保护模型，该模型在k-匿名的基础上加强了等价类中敏感属性种类的约束，减小了遭受同质性攻击的风险，而且在一定程度上还能够抵御背景知识攻击。Li等[7]提出了t-closeness(t保密)模型，该模型通过限定敏感属性的分布情况，在一定程度上可以抵制近似攻击[8]和偏态攻击[9]。我国在隐私信息保护领域的研究虽然起步比较晚，但也取得了不少成果。梅绍祖提出了限制信息收集结果之间的关系[10]的思想，这是中国最早对隐私保护进行的研究。滕金芳等[11]提出一种敏感属性l-多样性匿名化模型，这一模型通过聚类形成等价类簇，且构建等价类的敏感属性数量不小于l个，并满足各个种类个数区间为[l,2l-1]，以此来实现一种最优划分，从而保证发布数据的安全性。刘君强等[12]为解决云存储存在的数据安全问题，设计开发的匿名化算法具有全同态加密和全域泛化的特点，该算法对云存储的数据做出隐私保护等操作，能有效保证当前云存储环境下数据的隐私安全。邓秀勤等[13]提出一种基于节点分割的(a,k)-匿名算法，该算法对社交网络中带有隐私属性值的节点进行分割，使得节点特征被分割到两个节点里，降低了节点被攻击识别的可能性。J.Andrew等[14]提出一种结合k-匿名和拉普拉斯差分隐私技术的隐私保护方法(k,l)-匿名模型，这个匿名模型既保证了链接攻击的隐私性，又弥补了其他传统隐私保护机制的不足，并用公开数据集进行了验证。

本文通过分析研究发现当前的(k,l)-匿名隐私模型在进行泛化时通常都会出现过度泛化，从而造成信息的可用性降低，而且即使k-匿名过后准标识符之间仍存在隐含推理关系的风险。因此从医疗数据共享角度出发，本文在(k,l)-匿名模型的基础上，结合映射原理，提出了一种映射泛化的(k,l)-匿名模型。实验结果表明，该算法不仅能保护医疗数据的可用性，保护病人的隐私信息，而且能够大大提高泛化数据的可用性。

1 基于映射泛化的(k,l)-匿名算法

1.1 相关概念和匿名模型

1.1.1 基本概念

对于一个给定的具有有限行数的数据表T(A1,A2,…,An)，规定如下概念：

属性(A)：T的属性即为(A1,A2,…,An)。

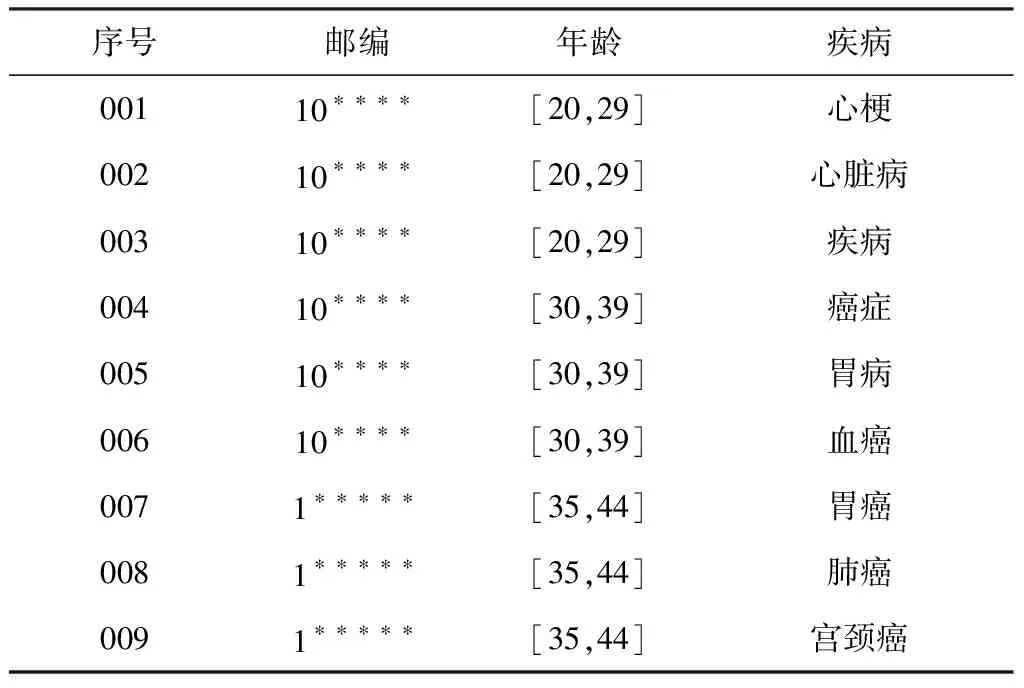
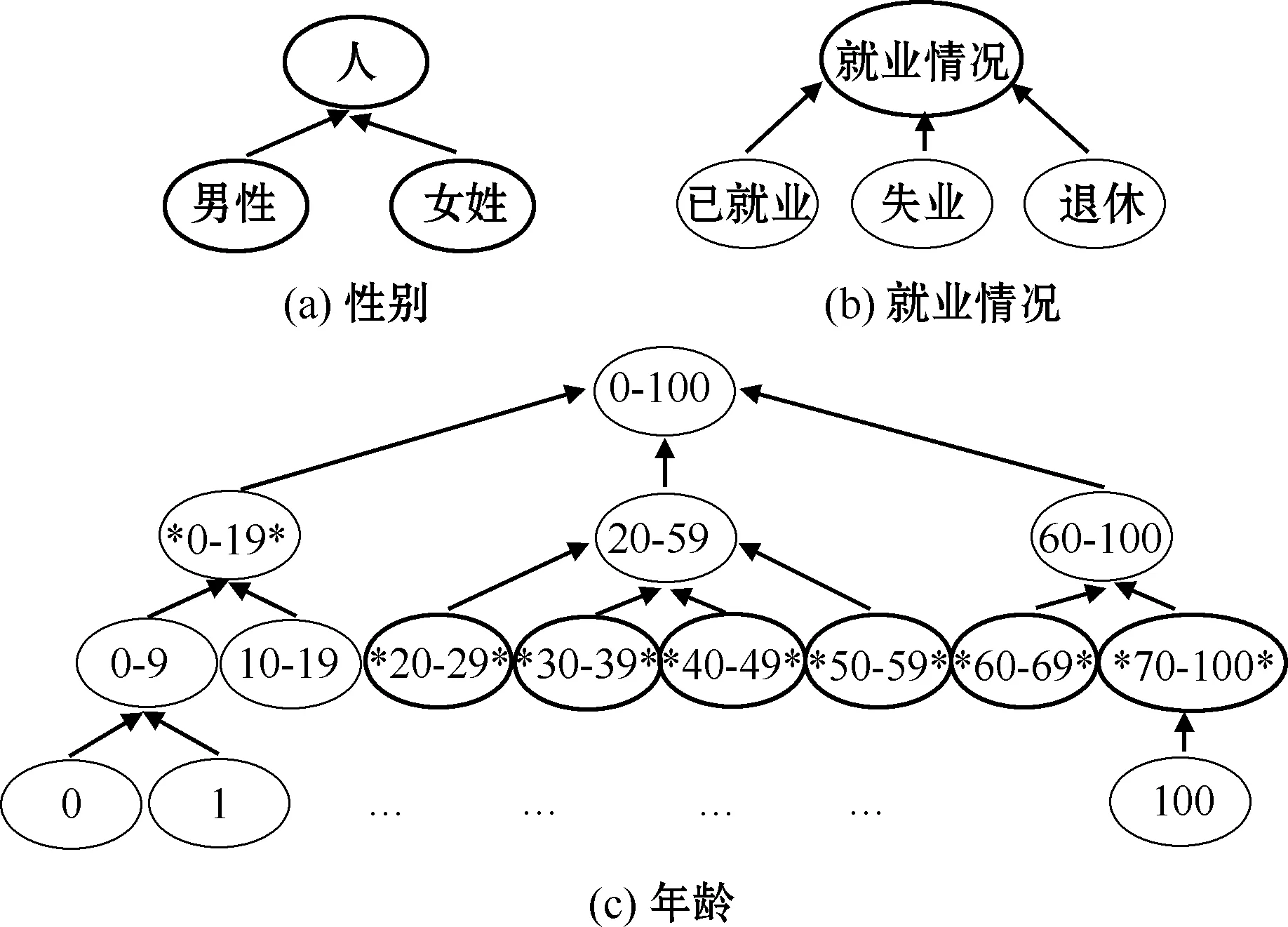
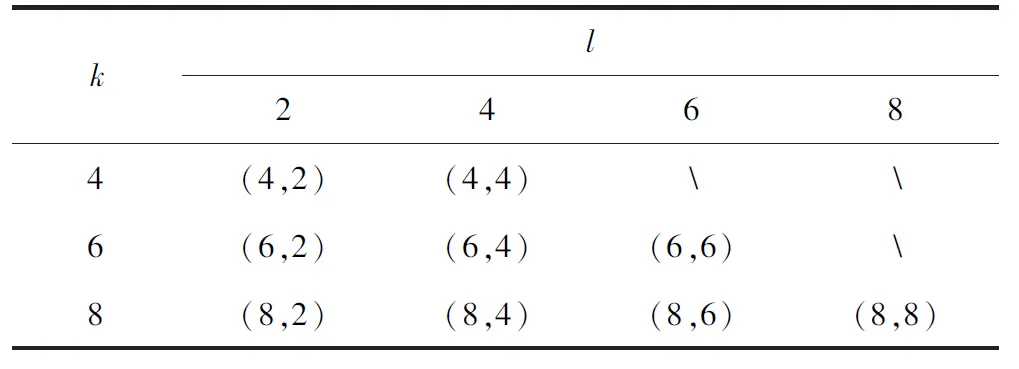
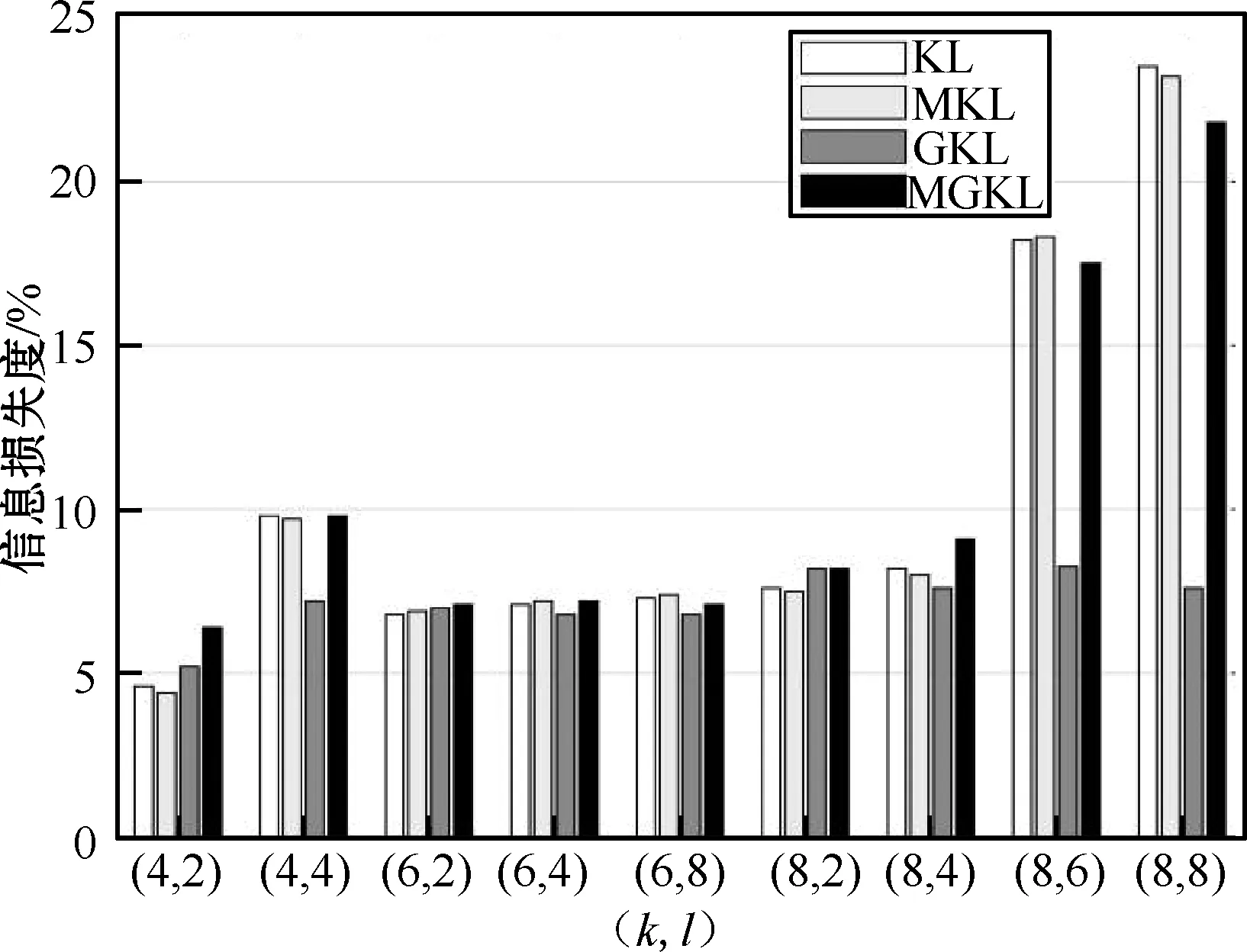
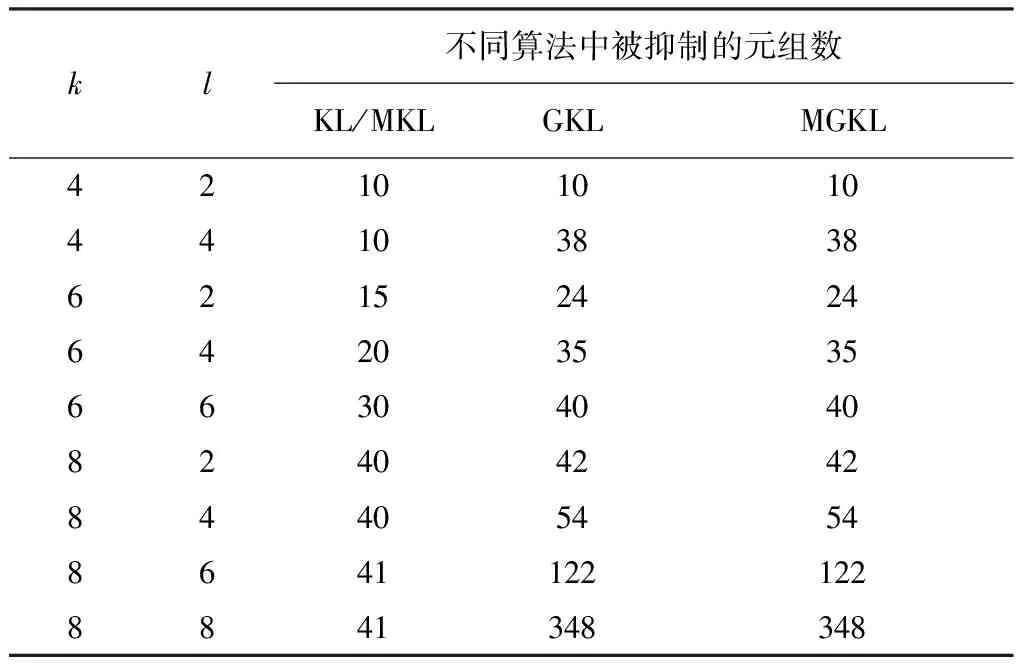
准标识符(QID)[15]：T中的一组最小属性集合(Ai1,Ai2,…,Aim) (i1

等价组(QIC)[16]：T中准标识符属性取值完全相同的记录组合在一起称为一个等价组。

泛化(Generalization)[17]：对T中的数据采用模糊的、抽象的值替代原始数据的方式称为泛化，即对数据进行更抽象、更概括的描述。

抑制(Fiction)[17]：对T中某些数据项进行删除使其不发布或是用特殊的符号来代替，例如“*”等。

k-匿名:A′是与T相关联的准标识符属性，当且仅当T[A′]中的每个值序列至少在T[A′]中出现k次，则称该数据表T满足k-匿名。

(k,l)-匿名：给定数据集Ω，在数据表T中，(k,l)-匿名在要求满足k-匿名的同时，还要求等价组中敏感属性的种类至少有l个，即等价组中至少有k个不同的元组，l个不同的敏感属性。

1.1.2 (k,l)-匿名模型

Li等[18]建立了(k,l)-匿名模型。满足k=3、l=3的(3,3)-匿名的患者信息表如表1所示。

表1 患者的(k,l)-匿名(k=3,l=3)信息表

1.2 基于映射泛化的(k,l)-匿名模型

(k,l)-匿名模型在进行医疗数据可信共享时存在敏感数据的过度泛化问题和推理泄露问题[19]。本文为了解决这两个问题，分别提出泛化约束(generalized constraint,GC)和映射关联(mapping association,MA)两种改进方法，组成基于映射泛化的(k,l)-匿名模型并形成面向医疗数据可信共享的映射泛化(k,l)-匿名算法。

1.2.1 过度泛化问题与泛化约束方法

匿名化算法总是以最小变化(信息损失比较少)对于原始数据集Ω进行保护，但是泛化后的属性值一般高于效用阈值[20]。超出阈值后，信息就会丧失作用，这不符合数据的可信共享原则。此外，当某属性列的敏感度高时，为了保证不被泄露，对其泛化层次较高，如对疾病属性列进行下一层次泛化，将各种病泛化为“部位+疾病”，如胃部疾病、肺部疾病和血液疾病等，虽然这种泛化能够充分保护患者隐私，但同时会使敏感数据失去数据的可用性，产生敏感数据的过度泛化问题。

本文通过对泛化边界值进行设置，防止出现该情形。首先考虑这样一种情形，目前一些研究人员想验证大部分病人是否在本地(市、县或镇的级别)的医疗机构进行检查和治疗，如若对省或国家的匿名表进行泛化操作，则研究就无法继续，故应将属性值的级别控制在市级以下。本文认为泛化边界以内的信息，都是可以被使用的数据信息。

在泛化约束方法中，SA表示一个敏感属性，GSA表示预先定义的泛化层[21]，对于每一个叶子值p，GC(p)位于叶子值到根节点值的路径上，在共享的数据中，p被允许的最大泛化值为GC(p)。对位置属性进行泛化的例子如图1所示，加*的节点值代表最大允许的泛化值。叶子值“固安县”的最大泛化值是“廊坊市”，“清河街道”和“庞各庄镇”的最大泛化值是“北京市”。这就意味着准标识符属性位置值“固安县”可以泛化到它自身也可以泛化到“廊坊市”，然而泛化到“海淀区”、“大兴区”、“北京市”都是错误的，也不能泛化到“河北省”和“中国”。而“清河街道”能够泛化到其本身或者“海淀区”和“北京市”，但是泛化到“中国”就是不正确的。如果叶子节点在泛化过程中存在多个可以泛化的值时选择最大值，但是如果只存在叶子节点不存在根节点的话，最大泛化值就为其自身。

图1 泛化约束示意

当存在匿名数据集既能够满足(k,l)-匿名，且准标识符属性值x的最大泛化值小于Vmax(x)，则数据集满足相关泛化约束的(k,l)-匿名。如原始数据集存在有年龄、婚姻状况和性别等准标识符属性和疾病情况这一敏感属性，准标识符属性特性与之相应的泛化层结构和最大被允许的泛化值如图2所示。

图2 准标识符属性对应的泛化层

患者的就诊信息初始表如表2所示。对表2进行(k,l)-匿名(k=3,l=2)操作后的就诊信息如表3所示。可以看到等价组(R4,R5,R6)和等价组(R2,R7,R9)中年龄对应的属性值高出其最大的泛化边界值，即过度泛化导致数据失去了可用性。对表3进行泛化约束操作后的就诊信息表如表4所示。

表2 患者就诊信息原始表

表3 (k,l)-匿名(k=3,l=2)后的患者就诊信息表

表4 经过泛化约束的(3,2)-匿名患者就诊信息表

1.2.2 推理泄露问题与映射关联方法

假设某医院患医疗信息表中有人患乳腺癌或者宫颈癌，虽然表格经过了(k,l)-匿名处理后发布，患者性别一栏经过了泛化处理，但是由于疾病隐藏性地包含有性别信息或性别倾向，攻击者可以据此做出性别推理，所以对性别的泛化和抑制在此情况下失效。

在映射关联方法中，给定数据表T(A1,A2,…,An)，对T中某一属性列(该属性列本身包含其他属性列的推理信息)中所有元素采用有规律的数字、字母、字符或它们的组合进行替代，同时生成一张与数字、字母、字符或它们的组合一一对应的关系映射关联表。

利用映射关联方法可将表4拆分成表5和表6两个子表，使得表5满足(3,2)-匿名的同时，准标识符属性中没有一个属性的泛化值超过Vmax(x)，并且攻击者无法通过某属性列推断出其他属性列的敏感数据。

表5 经过映射泛化的(3,2)-匿名患者就诊信息表

表6 映射关联表

1.2.3 基于映射泛化的(k,l)-匿名算法思想与流程

本文引入最大被允许泛化的数据集MAGD(maximum allowed generalization data)，其是数据表T的一个匿名集。在这个匿名集中，所有的准标识符属性值x都被泛化到Vmax(x)。借助原始数据集统一泛化到MAGD当中，能够对准标识符属性值的泛化范围进行控制，使其处在满足条件的范围之中，然后再对MAGD进行(k,l)-匿名，那么所有数据集就能够满足泛化约束的(k,l)-匿名的需求，最后对泛化约束后的(k,l)-匿名集中的敏感数据进行关联映射，防止通过某属性列推断出其他属性列的敏感数据。

结合医疗数据实例，基于映射泛化的(k,l)-匿名的算法流程为：

算法1:基于映射泛化的(k,l)-匿名算法输入:原始医疗数据集T,k,l,泛化约束值Vmax、Vmin,元组簇Tc、元组XNO,匿名集PkGC、P(k,l)GC、P(k,l)GC+MA,映射关联表TMA。输出:映射泛化后的(k,l)匿名集P′。Begin1 初始化:1.1 输入医疗数据集T1.2 根据数据集T设置k和l值1.3 设置泛化约束值Vmax、Vmin1.4 初始化元组簇Tc=ϕ、元组XNO=ϕ1.5 初始化匿名集PkGC=ϕ、P(k,l)GC=ϕ、P(k,l)GC+MA=ϕ2 泛化约束:2.1 将相关医疗数据集T的全部元组的准标识符属性值泛化为最大,形成能够最大允许的数据集MAGD2.2 计算极限的允许进行泛化的数据集MAGD,得到元组簇Tc,其约束边界值Vmax和Vmin2.3 对数据集MAGD不能达到条件的元组进行抑制操作,得到XNO3 (k,l)-匿名化:3.1 通过k值、泛化约束边界值Vmax和Vmin对元组簇Tc进行k-匿名化操作,得到匿名集PkGC3.2 通过l值对匿名集PkGC进行l-多样性操作,得到(k,l)-匿名集P(k,l)GC4 映射关联:4.1 采用映射关联方法对匿名集P(k,l)GC中敏感属性列中所有元素采用有规律的数字、字母、字符或它们的组合进行替代,同时生成对应的匿名集P(k,l)GC和关系映射关联表TMA4.2 合并匿名集P(k,l)GC和XNO,得到映射泛化后的(k,l)-匿名集P′,即P′=P(k,l)GC+MA∪XNO5 输出映射泛化后的(k,l)匿名集P′End

1.3 信息损失度量和多样性计算

匿名模型保护数据信息时会造成部分信息的损失，进而产生数据不准确的问题，即匿名代价。匿名代价是在进行数据泛化和抑制处理等过程中产生的，它是匿名化操作后信息缺少的指标，与此同时也能够对匿名后的数据集的优化情况进行判断。信息损失程度越低，则精度越高，其可用性越好，否则与之相反。故在完成匿名化操作过程里，应尽可能降低匿名付出的代价。本文借助泛化层级方式，对匿名代价进行衡量，而在此过程中，则需要对属性的泛化层级进行构建。每一个泛化层级所代表的信息量是存在差异的。一般情况下，对同一种属性，处于高层级的数据能够代表的信息量要少于处在低层级的数据。相关概念包括：

泛化信息(generalization information)：给定数据表T(A1,A2,…,An)，在数据表T中，元组簇Tc表示为{X1,X2,…,Xm}，准标识符属性的集合QID表示为{Q1,Q2,…,Qt}。Tc对应于QID的泛化信息为Gen(Tc)，对于每一个准标识符属性Qi，在{X1[Qi],X2[Qi],…,Xm[Qi]}对应的泛化层HQi中，Gen(Tc)[Qi]有最小的共同父节点。Gen(Tc)即Tc对应的满足泛化约束的准标识符属性信息。

例如，{Z0,Z1,Z2,Z3,Z4}展示的是邮编属性自下而上的泛化过程，每一层表示该属性的一个泛化层级，随着|hA|一直往上，属性的泛化程度越来越高，直到最后达到抑制的状态(全是*)：

Z4={******}

↑

Z3={100***}

↑

Z2={1001**,1002**}

↑

Z1={10010*,10019*,10021*}

↑

Z0={100100,100101,100191,100192,100213,100214}

1.3.1 信息损失度计算

Tc是来自于T中的一个元组簇，QID是准标识符属性的集合，G(Tc)是Tc的泛化信息，那么从Tc泛化到G(Tc)的信息损失度为

(1)

式中：|Tc|为元组簇中元组的数量；x为准标识符属性值；S(x)为从叶子节点x泛化到根节点泛化层HQi的子层；h(HQi)为泛化树层的高度；t为准标识符属性的数量。

1.3.2 匿名后整体信息损失度计算

原始医疗数据表T匿名化到满足泛化约束的(k,l)-匿名集P过程中会产生若干的等价组簇，这些簇整体信息损失度为

(2)

1.3.3 元组间多样性计算

为了使等价组中的敏感属性个数满足l个，必须要通过元组间的多样性来进行筛选，两个元组Xi、Xj的多样性可以通过式(3)和式(4)来表示。

(3)

(4)

1.3.4 元组和元组簇间的多样性计算

Xi和元组簇Tc间的多样性可以用式(5)和式(6)表示。

(5)

(6)

2 实验及结果分析

2.1 实验设置

2.1.1 实验数据集

本文实验数据基于数据科学竞赛平台Kaggle的医疗数据集[22]，整个数据集共有14个属性，共2 000条记录。为了方便说明问题，本文剔除数据集中相对不重要的部分属性，只保留6个准标识符属性和1个敏感属性。保留的准标识符属性分别为gender(性别)、dob(出生日期)、ancestry(出生地)、employment_status(就业状况)、education(教育情况)和marital_status(婚姻状况)，其中dob(出生日期)在本文中自动转化为age(年龄)。保留敏感属性为disease(疾病)，整个数据集中疾病的种类有13种(高血压、心脏病、前列腺癌、乳腺癌、皮肤癌、阿尔茨海默病、肾脏疾病、多发性硬化症、艾滋病、子宫内膜异位症、糖尿病、胃炎、精神分裂症)。

2.1.2 实验环境

本文实验环境设置如下：CPU：Intel Core i5;2.8 GHz主频;24.0 GB内存;Windows 1 064位操作系统；开发软件：eclipse2018开发平台。实验采用MySQL 5.0数据库来存储医疗数据，且算法用Java语言实现。

2.1.3 实验参数

本文实验参数设置如下：匿名k={4,6,8}，多样性l={2,4,6,8}，其实验组合有9种，如表7所示。本文用敏感权重来衡量敏感度，权重值越大，说明敏感度越高，其被泛化程度也越高，如表8所示。本文对全部的准标识符属性设置了泛化层，其中age的泛化层如图2(c)所示，其余如图3所示。

图3 除年龄外5个准标识符属性对应的泛化层

表7 映射关联

表8 疾病权重表

2.2 实验结果及分析

本文将基于映射泛化的(k,l)-匿名算法(简称MGKL)与原始(k,l)-匿名算法(简称KL)、带映射关联的(k,l)-匿名算法(简称MKL)以及带泛化约束的(k,l)-匿名算法(简称GKL)进行对比实验。所有算法的性能主要通过计算匿名化后信息的损失度以及各算法匿名化的运行时间来分析。

2.2.1 信息损失度对比

4种算法匿名化后信息的损失度如图4所示。

图4 各算法匿名化后信息的损失度对比

从图4可看出，随着k、l值的变化，与GKL和MGKL相比，KL和MKL的信息损失度大幅升高，主要因为KL和MKL之间不存在泛化约束条件的相关限制，并且有泛化过度的情况，因此信息的可用性下降。而随着k和l的值不断增大，匿名化后数据集中不满足k-匿名或者l-多样性属性的元组数也会相应增加，从而导致被抑制的元组数增加。实验中统计出了随着k、l变化时对应的被抑制元组数，如表9所示。

表9 随k、l变化被抑制的元组数

由表9可知，随着k和l的值不断增大，GKL和MGKL能有效增加抑制的元组数，防止数据集过度泛化。MGKL由于加入了映射关联方法，相比于GKL，同时能保证数据集的敏感数据不被推理泄露。

2.2.2 匿名化运行时间对比

4种算法匿名化的运行时间如图5所示。

图5 各算法匿名化的运行时间对比

由图5可知，GKL和MGKL的匿名化要比KL和MKL节约更多的时间，这是因为不设置泛化约束的状况需要更多次数据交换与筛选，如果数据量大，将会大幅降低算法的运行效率。同时，由于MKL和MGKL为了增加敏感数据的安全性需要进行映射关联操作，即将一张表映射为两张关联的子表，这就增加了算法运行的复杂度，所以MGKL和MKL的时间开销分别大于GKL和KL。

可见，MGKL无论是匿名化后的信息损失度还是匿名化的运行时间都要优于KL和MKL，虽然在匿名化的运行时间上差于GKL，但是GKL无法保证敏感数据不被推理泄露，易受到隐藏信息推理的攻击，没有良好的匿名保护作用。综上所述，从医疗隐私数据信息的安全性和可用性角度出发，基于映射泛化的(k,l)-匿名算法是一种更好的隐私保护模型。

3 结束语

本文从数据匿名化技术入手，针对(k,l)-匿名算法处理医疗数据后存在的敏感数据过度泛化问题和推理泄露问题等不足进行改进，提出了一种基于映射泛化的(k,l)-匿名模型并形成面向医疗数据可信共享的映射泛化(k,l)-匿名算法。实验表明，本文算法无论是在保证医疗数据的可用性、安全性方面还是在运行效率方面都存在明显的优点。不过本文算法需要在降低信息的损失度方面继续进行相应优化。此外，本算法实验是在单敏感属性条件下完成的，对于多敏感属性[23]的匿名保护也是接下来要重点考虑的问题。