无线传感器网络中敏感数据分布密度控制方法研究

蒋传健 唐祯蔚

摘 要： 为了解决传统基于参数可变遗传方法对无线传感网络敏感数据分布密度控制不健全，导致敏感数据分布密度失衡，且能量消耗过高的问题。提出基于改进差分蜂群算法的无线传感器网络节点分布密度控制方法，其综合考虑节点信息感知和信息传遞的能耗，对圆形区域和带状区域的节点能耗进行分析，从理论上分别给出适用于这两种场景的节点非均匀分布方法，在此基础上采用改进差分蜂群算法，通过以网络覆盖率为目标函数对覆盖区域的节点进行分布密度优化控制，实现节点中敏感数据分布密度的均衡控制。实验结果说明，所提方法可实现节点中敏感数据分布密度的均衡控制，降低能量消耗。

关键词： 无线传感网络； 节点； 敏感数据； 分布密度； 控制方法； 节点能耗； 蜂群算法

中图分类号： TN711?34； TP393 文献标识码： A 文章编号： 1004?373X（2018）07?0080?05

Research on distribution density control method for sensitive

data in wireless sensor networks

JIANG Chuanjian， TANG Zhenwei

（Chongqing Normal University Foreign Trade and Business College， Chongqing 401520， China）

Abstract： The traditional genetic method based on parameter variation has poor distribution density control for sensitive data in wireless sensor networks， which leads to the distribution density imbalance of the sensitive data and excessive energy consumption. Therefore， an improved differential bee colony algorithm based distribution density control method of wireless sensor network node is proposed， in which the energy consumptions of node information perception and information transfer are considered comprehensively. The node energy consumption of the circular area and zonal area is analyzed. The node nonuniform distribution method suitable for the above scenes is given in theory. On this basis， the improved differential bee colony algorithm is adopted， and the network coverage rate is taken as the target function to perform the distribution density optimization control for the node within the coverage area， and realize the distribution density balance control of sensitive data in the node. The experimental results show that the proposed method can realize the balance control of the distribution density of sensitive data in the node， and reduce the energy consumption.

Keywords： wireless sensor network； node； sensitive data； distribution density； control method； node energy consumption； bee colony algorithm

0 引 言

无线传感器网络是一项新兴技术，被广泛应用于国防、工业、环境、医疗等多个领域，一个典型的无线传感器网络是由大量具有感知能力的节点构成，节点上存很多数据信息，包括一些敏感数据信息。传统基于参数可变遗传方法对无线传感网络敏感数据分布密度控制不健全，导致敏感数据分布密度失衡，且耗费大量的资源。为解决该问题，本文采用基于差分蜂群算法的无线传感器网络节点分布密度控制法对节点进行能耗分析，实现节点的非均匀分布[1]，对节点中存储的敏感数据分布密度进行均衡控制。

1 无线传感器网络节点非均匀分布

1.1 节点能耗分析

无线传感器网络的敏感数据节点与传感器的接触区域有关系，一定面积内网络产生的敏感数据信息用[c bit（s×m2）]表示，各个节点的能量消耗由感知信息、发送信息和回传信息三部分组成，单位时间能源消耗的表达式如下：

式中：[b]表示单位时间内无线传感器接收的敏感信息量，[b]的值等于一定面积内产生的数据信息[c]和面积的乘积，面积用[A]表示；[α1]和[γ1]表示感知和接收单位的能量消耗；[β1]代表节点输送确定量比特的能量消耗[2]；[β2]代表路径不同消耗系数不同的常数；[n]代表路径，规定值为2或4。

将无线传感器的接触面积划分为不同的层，第[i]层的节点数用[Ni]表示，[Ei]表示第[i]层节点的能量消耗总量，用下面的算法计算不同层的单位时间能量消耗，所求[R]层总能量消耗由该层所有节点的感知消耗和发送信息消耗共同构成：

第[i]层[i]的取值范围是[1，R]，第[i]层的能量消耗还包括辐射外部数据产生的能量消耗，表达式如下：

为了得到各个节点上的敏感数据分布[3]，就要让各节点能量消耗相同，则节点存活时间为：

将上述两式进行转换可得：

1.2 节点非均匀分布

根据式（6）可知，一定范围内节点上敏感数据与节点能量消耗和区域大小有关[4]，在一定空间范围内，已知节点的能量消耗和网络规模后，节点间的比值关系可以确定，以下给出圆形区域和带状区域的节点间比例关系，圆形范围的面积计算公式为：

将式（8）代入到式（6）得出：[NiNi-1=（2i-1）+μ（R2-i2）（2i-1）+μ（R2-（i-1）2）=1+2-μ（2i-1）（2i-3）+μ（R2-（i-1）2）， 1≤i≤R] （9）

由式（7）得出，当[μ<2（2i-1）]时，发生[Ni>Ni-1]的情况，这种情况下[α1>γ1，]传感器感知信息是能量消耗的主要原因[5]，圆形区域的外部面积远大于内部面积，感知信息消耗的能量会更多，所以此时的外部就会出现较多的敏感数据，当出现[f=节点集所覆盖的网格数网格数]时，节点信息传递是能量消耗的主要原因，出现[Ni≤Ni-1]的情况，内部的能量消耗更多转发到外部节点[6]，内部会出现较多的敏感数据，则根据式（9）得出：

可以得出节点网络的生存周期为：

当无线传感网络节点的区域分布呈现带状，则有[Ai=Ai-1=H，][1≤i≤R]，得出：

带状区域下会出现[Ni

节点网络生存周期为：

以上内容通过传感器感知不同区域，利用能耗分析算法得出在一定网络环境下，节点数与节点能耗之间可以实现无线传感网络中节点的非均匀分布。在此基础上采用下文方法对无线传感网络节点分布密度实施优化控制，进而完成节点中敏感数据分布密度的均衡控制，降低网络节点能耗。

2 差分蜂群算法的无线传感器网络节点分布密

度控制法

2.1 节点编码设计

本文采用基于差分蜂群算法对1.2节完成非均匀分布的传感节点中的敏感数据分布密度实施均衡控制，为了实现敏感数据分布的健全性，以网络覆盖率为目标函数，维数[D=2N，][XY]表示单个个体，得到一种节点密度分布方案[X=x1，x2，…，xN，Y=y1，y2，…，yN，]个体的适应度用[f（XY）]表示，其中：

[f=节点集所覆盖的网格数网格数] （15）

节点编码设计如图1所示。

2.2 算法步骤

对无线传感网络节点种群进行初始化，则初始种群表示为：

式中：[j∈1，2，…，D；][Xjx]表示维度为[D]的分向量；[rand（0，1）]表示区间[0，1]内的任意数。

在种群附近搜索，根据式（17）寻找新的向量[Vi]：

式中：[k∈1，2，…，NP]，[k]和[i]的值都是随机产生且大小不同；[φji]为-1～1之间的随机数且[Vi∈Ω]。

差分策略可随机選取不同的向量，将其向量缩放后进行合成得到：

式中：[F]为缩放因子，在0～1之间；[r1，r2，r3]代表3个随机向量。交叉操作中新的分解向量[X′i]由[Xi]和[Vi]交叉得到：

式中：分解向量维度[j]是[1～D]的整数；CR代表交叉概率；[sn]代表任意维度。

基于差分蜂群算法对节点上产生的敏感数据进行分布密度控制的步骤如下：

1） 设[n=0，]根据式（16）得到初始的种群[X（0）]，根据种群得到向量的适应度值。

2） 由第[n]代种群[X（n）]求出分解向量[Xi，]对式（15）、式（19）进行差分进化法通过变形得到新向量[X′i，]且新向量的取值范围[X′i∈Ω，]求出新向量的适应度值用[f（X′i）]表示。

3） 新向量的适应度值与原向量的适应度值相比，若大于原向量适应度值，用新向量的适应度值代替原向量的适应度值，若不是则保持不变[9?10]。

4） 计算[Xi]的适应度值，再求出各个分解向量的概率[P。]

5） 随机选择一个分解向量，按照[Vji=][Xjr1+F（Xjr2-Xjr3）]在这个向量的周围进行搜索，得到新的向量[Vi]，同时保证新向量[Vi∈Ω，]计算新向量的适度值用[f（Vi）]表示。

6） 利用比较值选择法，将[Vi]和[Xi]中适应度值进行比较，若[Vi]的适应度值大于[Xi]的适应度值，用[Vi]代替[Xi，]将得到结果作为节点敏感数据的最优适应度值[f_best，]得到对应参数[（x1，x2，…，xn）]。

7） 若分解向量的周围向量搜索全部完成，没有找到最优结果，根据上文[Vji=Xjx+φji（Xji-Xjk）]把该向量进行替换。

8） 假设[n]等于最大迭代数[Gmax，]停止运算得到最优的适应度值[f_best]和[（x1，x2，…，xn）]。

通过上述过程对本文中的无线传感网络非均匀分布的节点分布密度实施优化控制，其中编码设计提高了控制效率，算法步骤的细化实现了节点中敏感数据分布密度的均衡控制。

3 实验分析

为了验证本文方法的控制性能，采用Matlab对三种检测方法进行测试。将线圈个数NP=40的无线传感器网络节点置入到边长为100 m的正方形检测区域内，已知传感器网络感知节点半径为12 m，将检测区域划分为100个大小相同的正方形区域，将最大迭代数定为500，实验采用本文方法、基于参数可变遗传方法以及基于蝙蝠优化方法对实验区域敏感数据分布密度实施100次控制，进而验证方法能够有效控制敏感数据的分布密度。

本文方法将NP固定为15，最大迭代次数为120；基于参数可变遗传方法的NP也固定为15，最大迭代次数为100；基于蝙蝠优化方法的NP为10。三种方法对覆盖区域中节点敏感数据分布密度实施控制，本文方法在88次迭代后得到最优的密度分布曲线，基于参数可变遗传方法在第196次迭代后得到最优的密度分布曲线，基于蝙蝠优化方法无法得出最优分布，实验结果如图2所示。

对三种检测方法重复进行100次，根据结果计算出密度分布的平均数、标准差和最差值得出的数值制作成如表1所示的三种方法的运行结果。

从表1可以得出，无论从哪个角度来看，本文方法的节点分布密度效果都要好于基于参数可变遗传方法和基于蝙蝠优化方法，能够实现敏感数据的完全分布密度控制。从图2可以看出，本文方法对敏感数据的密度控制收敛速度快，节点分布密度覆盖范围广，可以避免局部区域数据冗杂。

为进一步验证本文方法对敏感数据的均衡控制效果，设计节点散播密度的网络仿真实验，图3是不同方法下的节点密度变化曲线。

从图3中能够得出，节点在随机分布的模型下，节点上敏感数据的分布密度要达到90%以上的概率，本文方法一共需要安装35个无线传感网络，基于参数可变遗传方法和基于蝙蝠优化方法都至少需要40个无线传感网络。若要实现节点的完全覆盖本文方法需要40个无线传感器网络，基于参数可变遗传方法和基于蝙蝠优化方法需要50个。说明可通过更少的节点数达到更高的网络覆盖率。

节点感知范围半径的大小也会影响节点分布密度变化曲线，图4是在节点数为40个情况下，不同控制方法下感知半径变化对节点密度变化曲线造成的影响。

从以上实验结果可以得出，一定数量的节点分布在一定范围的区域时，在无线传感网络节点感知半径逐渐增大的情况下，本文方法的网络节点分布密度较其他两种方法领先，三种方法同时都达到覆盖率100%时的感知半径为13 m。

图5和图6对控制方法下初始节点和最终节点的敏感数据分布进行对比，初始情况下无线传感网络节点上敏感数据的分布杂乱无章，在经过本文方法的作用下，敏感数据分布密度变得清晰，有规律可寻，事实证明了本文方法可以对无线传感网络中的敏感数据进行均衡分布控制。

表2是三种方法在无线传感器节点为40个时，传感区域为10 m×10 m的正方形区域内，初始节点能量和最终节点能量的对比情况，由表2数据可以得出，本文方法相较于其他两种方法消耗的能量较少。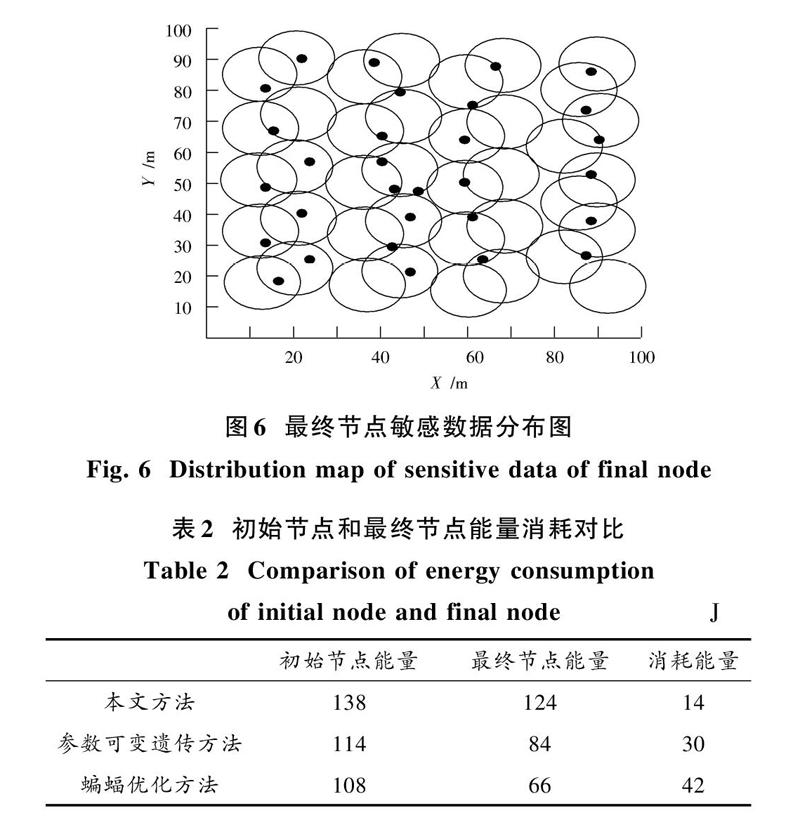

4 结 论

本文对无线传感器网络敏感数据分布密度控制问题进行研究，采用基于差分蜂群算法的无线传感器网络节点分布密度控制方法，提高了节点上敏感数据的分布密度控制效率，实现了节点中敏感数据分布密度的均衡控制，减少了能量消耗。

参考文献

[1] 成國营，王艳.无线传感器网络中多移动Agent协同控制数据分流方法[J].计算机应用，2015，35（4）：910?915.

CHENG Guoying， WANG Yan. Multi?mobile Agent collaborative control data separation method in wireless sensor network [J]. Journal of computer applications， 2015， 35（4）： 910?915.

[2] 袁飞，詹宜巨，王永华.无线传感器网络中数据密度相关度融合算法[J].控制理论与应用，2014，31（11）：1568?1573.

YUAN Fei， ZHAN Yiju， WANG Yonghua. Data density correlation degree based aggregation algorithm in wireless sensor network [J]. Control theory & applications， 2014， 31（11）： 1568?1573.

[3] 熊伟丽，刘欣，陈敏芳，等.基于差分蜂群算法的无线传感器网络节点分布优化[J].控制工程，2014，21（6）：1036?1040.

XIONG Weili， LIU Xin， CHEN Minfang， et al. Node distribution optimization in wireless sensor networks based on differential bee colony algorithm [J]. Control engineering of China， 2014， 21（6）： 1036?1040.

[4] 徐立鸿，早明华，蔚瑞华，等.温室无线传感器网络节点发射功率自适应控制算法[J].农业工程学报，2014，30（8）：142?148.

XU Lihong， ZAO Minghua， WEI Ruihua， et al. Adaptive control algorithms of transmitting power for greenhouse WSN nodes [J]. Transactions of the Chinese society of agricultural engineering， 2014， 30（8）： 142?148.

[5] 及歆荣，侯翠琴，侯义斌.无线传感器网络下线性支持向量机分布式协同训练方法研究[J].电子与信息学报，2015，37（3）：708?714.

JI Xinrong， HOU Cuiqin， HOU Yibin. Research on the distri?buted training method for linear SVM in WSN [J]. Journal of electronics & information technology， 2015， 37（3）： 708?714.

[6] 游子毅，章俊华，陈世国，等.基于无线传感网络的数据融合方法及其在智能交通系统中的应用研究[J].计算机应用研究，2014，31（6）：1719?1722.

YOU Ziyi， ZHANG Junhua， CHEN Shiguo， et al. Data aggregation scheme based on wireless sensor networks and its application research in intelligent transportation system [J]. Application research of computers， 2014， 31（6）： 1719?1722.

[7] 孙泽宇，李传锋，邢萧飞，等.联合感知无线传感网的优化覆盖控制算法[J].西安交通大学学报，2016，50（10）：86?92.

SUN Zeyu， LI Chuanfeng， XING Xiaofei， et al. An optimal coverage control algorithm with joint sensing for wireless sensor networks [J]. Journal of Xian Jiaotong University， 2016， 50（10）： 86?92.

[8] 蒋文贤，缪海星，王田，等.无线传感器网络中移动式覆盖控制研究综述[J].小型微型计算机系统，2017，38（3）：417?424.

JIANG Wenxian， MIAO Haixing， WANG Tian， et al. Survey on coverage control with mobile elements in wireless sensor networks [J]. Journal of Chinese computer systems， 2017， 38（3）： 417?424.

[9] 孙泽宇，伍卫国，王换招，等.无线传感器网络基于参数可调增强型覆盖控制算法[J].电子学报，2015，43（3）：466?474.

SUN Zeyu， WU Weiguo， WANG Huanzhao， et al. An enhanced coverage control algorithm for wireless sensor networks based on adjustable parameters [J]. Acta electronica sinica， 2015， 43（3）： 466?474.

[10] 王建平，薛雪，孙伟.智能配电网无线传感器网络数据通信的QoS?MAC层模型[J].电力系统自动化，2014，38（9）：160?167.

WANG Jianping， XUE Xue， SUN Wei. QoS?MAC model of wireless sensor networks for smart distribution power grid data communication [J]. Automation of electric power systems， 2014， 38（9）： 160?167.