一种基于二分法和SDFT的FMCW雷达高精度测距方法

魏晓会 谢锡海

摘 要： 为了提高FMCW雷达的测距精度，提出一种将SDFT结合二分法来提高峰值频率点的搜索方法。该方法克服了传统FFT固有采样间隔导致的测距误差问题，首先利用FFT处理将谱峰值限定在两个频点之间，然后采用二分法和SDFT逐步搜索峰值，在不增加太大计算量的条件下进一步提高差频信号的谱分析精度，进而提高了测距精度。最后通过仿真分析验证了该方法的有效性，满足了高精度测距的实际需要。

关键词： 频率估计； 二分法； SDFT； FMCW雷达； 差频信号； 测距方法

中图分类号： TN959?34 文献标识码： A 文章编号： 1004?373X（2018）07?0008?04

A dichotomy and SDFT based high?precision range?finding method of FMCW radar

WEI Xiaohui， XIE Xihai

（School of Communication and Information Engineering， Xian University of Posts and Telecommunications， Xian 710061， China）

Abstract： In order to improve the range?finding accuracy of the FMCW （frequency modulated continuous wave） radar， a method combining SDFT （shifted discrete Fourier transform） and dichotomy is proposed to search the peak frequency point， which can reduce the range?finding error caused by the inherent sampling interval of traditional FFT. The FFT processing is used to limit the spectral peak within two frequency points， and then the dichotomy and SDFT are used to search the peak value step by step， which can further improve the spectrum analysis accuracy of the difference frequency signal and range?finding accuracy without increasing the calculation amount. The validity of the method was verified with simulation analysis. The simulation results show that the method can meet the practical demands of high?precision range?finding.

Keywords： frequency estimation； dichotomy； SDFT； FMCW radar； difference frequency signal； range?finding method

0 引 言

线性调频连续波（Frequency Modulated Continuous Wave，FMCW）雷达由于其自身的良好特性，被广泛应用到各个领域[1?5]，而测距就是其最重要的功能之一，因此，对FMCW雷达高精度测距的研究也越来越重要。FMCW雷达测距固定误差受扫频带宽的限定，信号处理过程中的快速傅里叶变换（Fast Fourier Transform，FFT）频谱估计精度受到FFT频率量化的限制，在测量精度要求越来越高的场合下存在栅栏效应。直接利用FFT频谱估计目标距离显然无法达到其精度要求。如通过采用FFT插值法增大运算点数来减小频率的采样间隔将大大增加数字信号处理的运算量，从而影响实时性。文献[6]在传统FFT处理的基础上，将谱峰值限定在两个频点之间，然后利用Chirp_Z变换对峰值可能存在的频谱范围进行细化，进一步提高FMCW的测距精度，且计算效率远高于FFT插值的方法。为了进一步提高测距精度和计算效率，本文提出一种采用二分法迭代搜索结合移位离散傅里叶变换（Shifted Discrete Fourier Transforms，SDFT）寻找频谱峰值的方法，该方法首先需要FFT处理，然后在谱峰存在的两个频点之间采用二分法和SDFT逐步搜索峰值，在不增加太大计算量的条件下，进一步提高差频信号的谱分析精度，进而提高了测距精度。最后通过计算机仿真验证了本文所提算法的有效性，因此具有较大的工程实用价值。

1 FMCW雷达测距原理

FMCW雷达工作时，通过调频信号发生器产生调频信号作为发射信号，经天线向外发射，还有一部分作为本振信号，当遇到目标后就会反射回来，回波信号与直接耦合来的本振信号加入混频器，在混频器输出端便有了差频信号。差频信号的频率包含目标距离和速度等信息。

FMCW雷达调频信号可设置成锯齿波、三角波和正弦波，下面以三角波为例说明FMCW雷达测距原理。如图1所示是三角波调制的发射信号、接收信号以及差频信号的频率变化示意图。

由图1可以看出，回波信号与发射信号频率图形状相同，只是时间上有延时，延迟时间与目标距离[R]的关系为：

根据图1中的三角关系可知：

因此得到距离[R]为：

[R=cTm4ΔFmfi] （3）

式中：c为光速；[fi]为差频信号频率；[Tm]是三角波的周期。在调制参数[ΔFm，][Tm]一定的条件下，差频信号频率[fi]与距离[R]成正比，测得差频信号频率即可计算出距离[R。]因而精确地从差频信号中提取出所包含的高度信息成为关键。

2 SDFT的基本原理

设点数为[N]的离散时间信号[x（n）]，它的[N]点DFT记为[X（k）]：

[X（k）=n=0N-1x（n）exp（-j2πNnk），k=0，1，2，…，N-1] （4）

而它的[N]点SDFT记为[Xnl（k）]：

[Xnl（k）=n=0N-1x（n）exp-j2πNk+lMn，k=0，1，2，…，N-1] （5）

式中：[M]为提前设好的常数；[l]取[0，1，2，…，M-1，]当[l=0]时，SDFT就是一般的DFT，当[l≠0]时，SDFT与DFT不同。它们的重要不同是所分析的[N]个谐波频率不同。DFT分析的[N]个谐波频率为[2πNk，k=0，1，2，…，N-1；]而SDFT分析的[N]个谐波频率为[2πNk+lM，k=0，1，2，…，N-1。]取不同的[M]值，这[N]个谐波频率也不同，因此，SDFT的谐波频率可以看成是随[l]可变的。对DFT而言，当[N]一定时，谐波频率的位置就是固定不变的；对于周期信号而言，在无噪声的情况下DFT可以进行准确的频率估计，但前提是[N]和序列周期要是整数倍。实际中，做到这一点是非常困难的，一是所分析的信号频率未知，二是点数[N]在实际应用中不能轻易更改。当有噪声时会更进一步降低信噪比。

SDFT相比DFT能较好地解决这个问题[7?8]。它的思路相当于设计一组中心频率可变的窄带滤波器组，使信号的频率等效于其中一个窄带滤波器的中心频率，在这种情况下，该滤波器的信号输出最大，其他的窄带滤波器输出最小。

3 二分法结合SDFT

通过上节分析可知，通过合理的设置SDFT中的[M]和[l]值，可以计算任意频点处的频谱值。为了提高FMCW雷达测距精度，设置[M=2，l=1，]可以计算两个频点中间处的频谱值，这样结合二分法[9?10]进行搜索，每搜索一次，测距精度提高1倍。该算法流程如图2所示。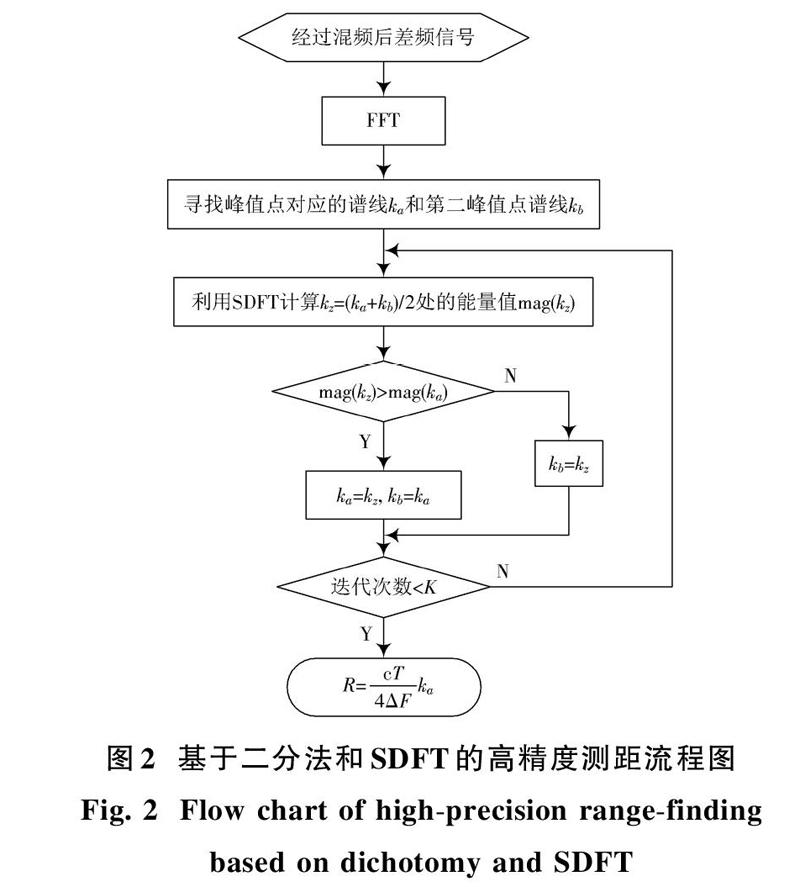

基于二分法和SDFT的高精度测距的主要步骤如下：

1） 将收到的雷达回波信号进行混频处理得到差频信号，然后对差频信号进行傅里叶变换；

2） 寻找峰值点对应的谱线[ka]和第二峰值点谱线[kb，]能量值分别记为[mag（ka）]和[mag（kb），]根据能量重心原理，真实峰值点应该在谱线[ka]和[kb]之间，利用SDFT[（M=2，l=1）]计算谱线[ka]和[kb]中间谱线[kz]处的能量值[mag（kz），]其中[kz=ka+kb2；]

4 仿真分析

为了验证本文算法的有效性，采用Matlab仿真的方法进行验证，设雷达载波频率为24 GHz，采样频率为100 kHz，数据长度为[N=256，]频率采样间隔为390.625 Hz，目标距离设置为14.7 m，对FMCW回波信号进行混频后得到差频信号，对差频信号直接进行FFT得到如图3所示的仿真结果，通过式（3）计算可得目标距离为14.65 m，误差为-0.05 m。峰值处对应的第20个频点，频率为7 812.5 Hz，第二峰值点对应的第21个频点，频率为8 203.125 Hz，在频率7 812.5～8 203.125 Hz之间进行64点Chirp_Z变换得到如图4所示的仿真结果，峰值频率为7 843.500 2 Hz，对应目标距离为14.706 6 m，误差为0.006 6 m。

本文利用二分法进行谱峰搜索，搜索速度较快，每计算一次距离计算精度提高至原来的2倍，迭代计算6次，可以提高64倍，精度和搜索次数成指数关系。在本文仿真中迭代次数[K]为6，每次迭代输出的距离误差如表1所示。从表1可以看出，随着迭代次数的增大，测距误差逐渐减小，6次迭代测距误差为0.005 7 m，测距精度高于64位Chirp_Z变换。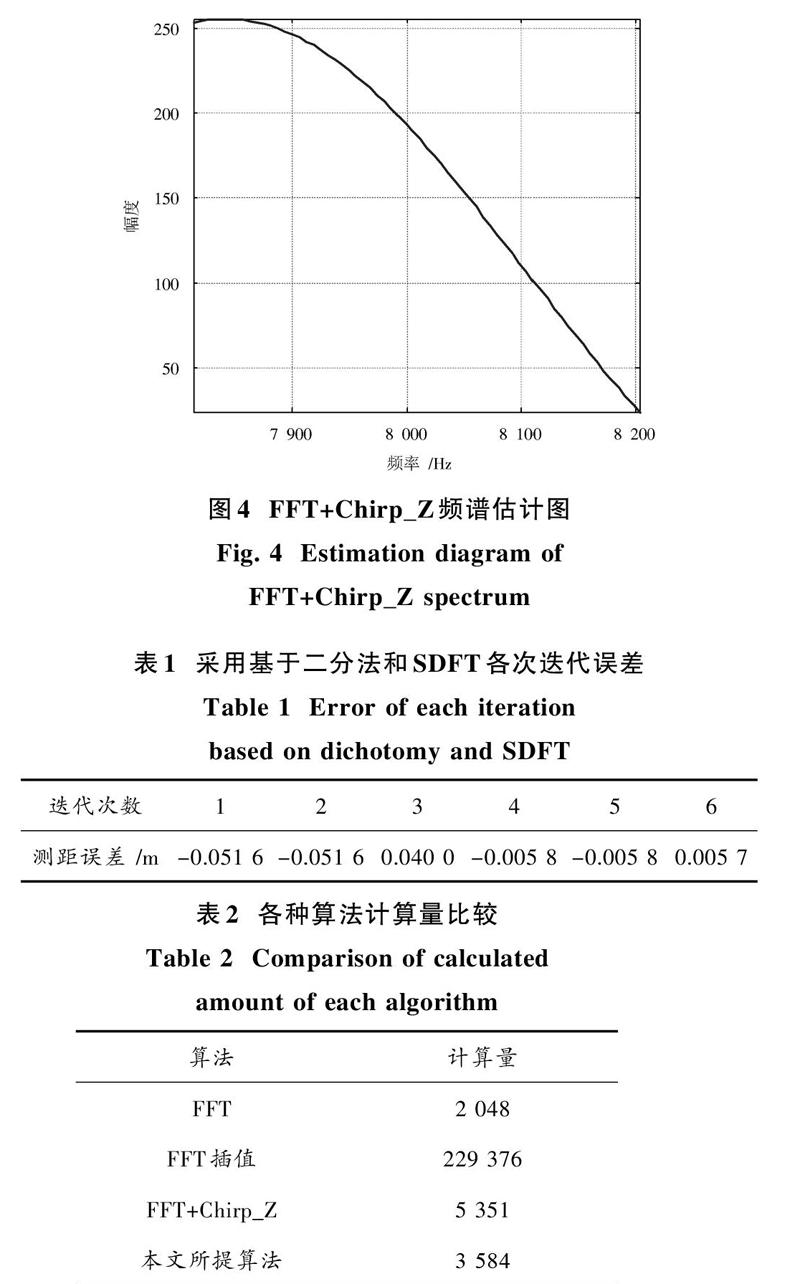

5 计算量分析

由参考文献[6]可知，FFT的计算量为[Nlog2N，]因此若直接进行[M]倍FFT插值来提高测距精度需要的计算量为[MNlog2MN，]Chirp_Z的计算量为[2（M+N）+][（M+N）log2（M+N），]由于在Chirp_Z变换前需要进行一次FFT，所以总的计算量为[Nlog2N+2（M+N）+（M+N）?][log2（M+N），]而本文所提算法首先也需要进行一次FFT，然后需要计算[log2M]次的SDFT，计算一次SDFT需要的复乘计算量为[N，]因此共需计算量为[Nlog2N+Nlog2M。]假设[N=256，M=64，]各种算法的计算量如表2所示。

可见，FFT插值計算量最大，是FFT+Chirp_Z算法的近43倍，而FFT+Chirp_Z算法是本文所提算法的1.5倍。且随着[M]的增大，本文所提算法的效率会进一步提高。当[M=512]时，FFT+Chirp_Z算法是本文所提算法的2.5倍。

6 结 语

从仿真与计算量分析可以看出，将SDFT结合二分法的方法要比普通FFT方法以及FFT+Chirp_Z方法更能提高谱分析的精度，大大减小误差，并且算法结构简单易于实现，因此可以用来提高FMCW雷达高度表的测距精度。

参考文献

[1] 鲁晓帆.FMCW测距雷达设计与实现[D].南京：南京航空航天大学，2012.

LU Xiaofan. Design and implementation of FMCW range?finding radar [D]. Nanjing： NUAA， 2012.

[2] STOVE A G. Linear FMCW radar techniques [J]. IEE procee?dings of radar & signal processing， 1992， 139（5）： 343?350.

[3] MCGREGOR J A， POULTER E M， SMITH M J. Switching system for single antenna operation of an S?band FMCW radar [J]. IEE proceedings of radar sonar and navigation， 1994， 141（4）： 241?248.

[4] BURROWS G D. An assessment of a FMICW ground?wave radar system for ocean wave studies [J]. International journal of remote sensing， 1985， 6（1）： 275?282.

[5] 赵爽.汽车毫米波防撞雷达的研究与实现[D].长春：长春理工大学，2013.

ZHAO Shuang. Design and implementation of MMW anticollision radar for automobile [D]. Changchun： Changchun University of Technology， 2013.

[6] 李天昀，葛临东.两种快速频域细化分析方法的研究[J].系统工程与电子技术，2004，26（9）：1192?1194.

LI Tianyun， GE Lindong. Research of two kinds of fast zoom spectrum [J]. Systems engineering and electronics， 2004， 26（9）： 1192?1194.

[7] 罗建，肖妮.用SDFT实现FSK调制信号的数字解调方法[J].无线通信技术，2007，16（1）：60?62.

LUO Jian， XIAO Ni. Study of the method of SDFT demodulation for the FSK signal [J]. Wireless communication technology， 2007， 16（1）： 60?62.

[8] YAROSLAVSKII L P. Shifted discrete Fourier transforms [J]. Problems of information transmission， 1980， 15： 102?105.

[9] 丁康.离散频谱分析校正理论与技术[M].北京：科学出版社，2008.

DING Kang. The principle and technology of discrete spectrum correction [M]. Beijing： Science Press， 2008.

[10] 崔刚，李涛.一种基于二分法的LFM调制斜率估计算法[J].电子科技，2015，28（10）：15?17.

CUI Gang， LI Tao. An estimation algorithm based on the dichotomy of LFM modulation slope [J]. Electronic science and technology， 2015， 28（10）： 15?17.