考虑颗粒转矩的接触网络诱发各向异性分析1)
王怡舒 沈超敏 刘斯宏,2) 陈静涛
*(河海大学水利水电学院,南京 210098)
†(中国建筑第二工程局有限公司,上海 200135)
引言
颗粒材料是由大量相互接触的离散颗粒组成的系统[1],其宏观力学行为与内部颗粒间复杂接触密切相关,而基于连续介质力学的唯象描述主要建立在颗粒材料宏观物理试验的基础上,不能追踪颗粒间的相互作用.离散单元法(discrete element method,DEM)[2]作为研究颗粒材料内部接触结构(组构)特性的一种有效模拟方法,被广泛用于探究颗粒材料细观与宏观力学特性的联系[3-6].从细观角度出发,研究颗粒间的传力机制[7],并建立宏细观尺度间的联系,是研究颗粒材料宏细观力学性质的必要方法.
颗粒材料内部力的传递通过颗粒间的接触实现,在外部载荷的作用下,当接触点处的切向接触力大于最大静摩擦时,形成滑动接触;另一方面,由于颗粒形状的不规则性,在颗粒转动过程中会产生抗转动力矩,当颗粒点的转动力矩大于最大抗转动力矩时,形成转动接触.采用滑动摩擦和抗转动力矩是反映颗粒材料的摩擦性和抗转动特性的重要途径,被广泛应用于颗粒材料的理论模型和数值模拟中[8-11],如在DEM 模拟时,为了考虑颗粒的粗糙程度,颗粒的接触通常设置Mohr-Coulomb 摩擦,为了考虑颗粒形状的影响则在颗粒接触模型中引入抗转动力矩[12-13].
颗粒间接触也可以根据法向接触力的大小,采用平均法向接触力的大小作为分界线,将体系的接触分为大于平均法向接触力的强接触和小于平均法向接触力的弱接触,相互连接形成的强弱力链网络抵抗外部载荷[14-15],该分类方法被很多学者采用[3,16-18].目前,一些学者发现滑动接触对颗粒材料的宏观力学行为影响深刻,如Aloso-Marroquin 等[19]认为滑动接触对颗粒材料的塑性行为非常重要,可以将全局接触划分为非滑动-滑动接触网络,以便理解颗粒体系的宏观力学响应.此外,研究发现强弱力链扮演的角色也有所差异,Radjai 等[14]指出强接触对宏观力学响应有着决定性的影响,强接触承担全部偏载荷,而几乎所有的摩擦耗散发生在弱接触.与滑动接触形成较鲜明对比的是,尽管转动接触对真实颗粒的动力学影响显著,目前针对转动接触力链的类似研究较少.
颗粒材料细观尺度组构各向异性的产生及变化是其宏观尺度各向异性力学特征的本质原因,组构各向异性分为两类:原生各向异性和诱发各向异性,原生各向异性是材料的固有属性,在岩土材料中典型表现为横观各向同性和沉积面铅直方向的各向异性,由颗粒本身的性质(裂隙或者孔隙)以及沉积过程造成;诱发各向异性随着应力状态的改变而发生变化.各向异性可以通过颗粒接触的组构张量定量表征,Oda[20]较早提出了组构张量的概念定量统计组构各向异性;在此基础上,Rothenburg 等[21-22]首先推导了二维颗粒体系的诱发各向异性表达式,并提出了颗粒材料应力-接触力-组构理论关系;Chantawarangul[23]推导了三维条件下的应力-接触力-组构关系;Zhao和Guo[24]初步揭示了颗粒材料中组构各向异性与宏观应变局部化的直接联系.各向异性与颗粒内部的接触类型密切相关,Sufian 等[25]将颗粒体系中的接触网络分为非滑动-强接触、非滑动-弱接触、滑动-强接触和滑动-弱接触,发现非滑动-强接触的组构各向异性参数对颗粒材料抗剪能力的贡献最大,在不同应力路径下偏应力比与非滑动-强接触的组构各向异性参数具有唯一的线性关系.然而,目前关于抗转动效应对不同子接触网络的组构各向异性演变规律的影响仍缺乏系统的研究.
本文根据剪切过程中颗粒接触点的滑动与否、转动与否和强弱力情况,将全局接触网络分为不同的子接触网络.基于不同抗转动系数下颗粒材料的常规三轴剪切试验数值模拟结果,分析剪切过程中不同子接触网络的组构张量的演变规律,并探究抗转动系数对子接触网络的各向异性演变规律及对宏观应力的贡献程度的影响.
1 DEM 模拟试验
1.1 颗粒接触模型
颗粒间的相互作用可用接触法向n、枝向量b、法向接触力fn、切向接触力ft等矢量进行描述.接触法向指颗粒接触点处切平面外法线方向,可用其方向余弦表征;枝向量是指两接触颗粒几何中心的连线,b=(R1+R2)n,其中R1和R2分别为两接触颗粒的半径;颗粒间的法向和切向接触力分别指两接触颗粒沿接触法向和在接触切平面上的接触力,如图1(a)所示.在进行离散元数值模拟时,考虑颗粒抗转动效应的线性接触模型[26]包括3 个部分:法向、切向和转动接触模型,如图1(b)所示.
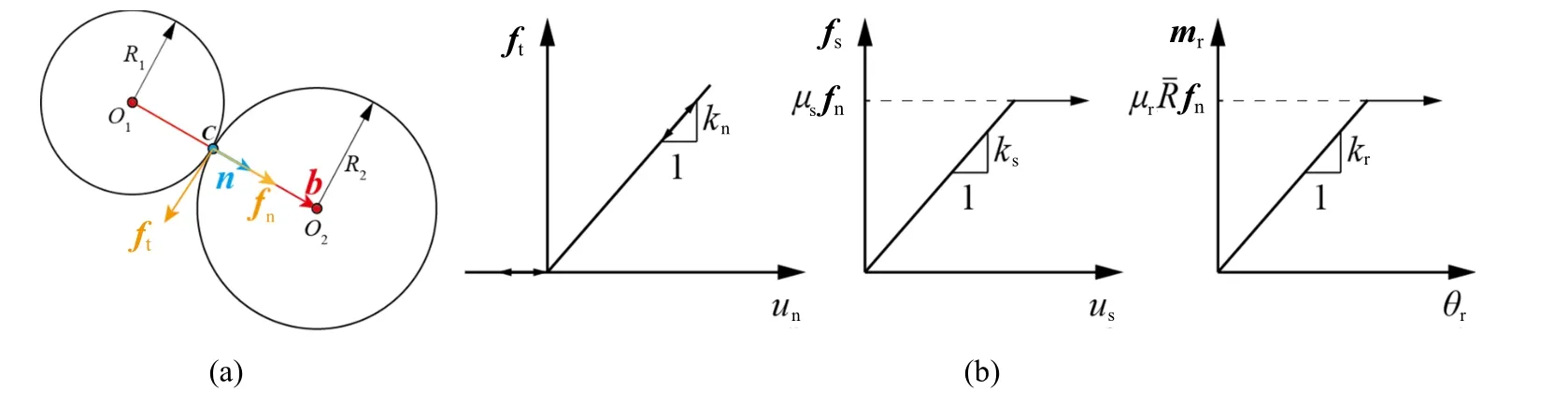
图1 抗转动-线性接触模型Fig.1 Linear-based rolling resistance contact model
颗粒间的法向接触力和切向接触力分别用下式进行计算
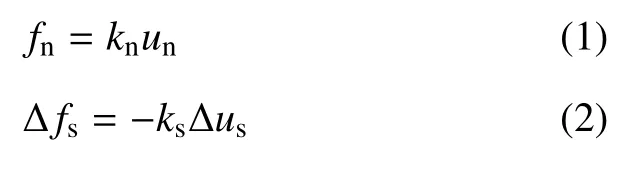
式中,fn,kn和un分别为法向接触力、法向接触刚度和法向重叠量;Δfs,ks和Δus分别为切向接触力增量、切向接触刚度和切向相对位移.颗粒间法向接触刚度kn和切向接触刚度ks可根据下式计算[26]

式中,E为颗粒弹性模量,A和L分别为接触点处的横截面积和长度,A=πr2,r=min(R1,R2),L=R1+R2;κ*为刚度比.当计算的切向接触力fs大于最大静摩擦μsfn时,颗粒间发生滑动,此时的颗粒接触为滑动接触.滑动接触点的切向接触力fs=μsfn(μs为颗粒间滑动摩擦系数).
转动接触模型[27-28]主要是通过在颗粒间加入一个抗转动力矩mr,其定义为

式中,θr为颗粒间相对转角;kr为颗粒转动刚度,与切向接触刚度ks相关,可按下式计算
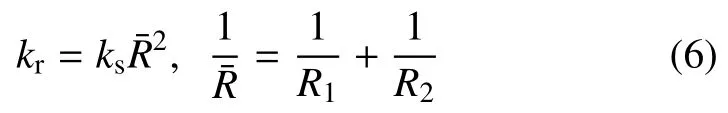
当颗粒点的转动力矩mr大于最大抗转动力矩时,颗粒间发生相对转动,此时的接触为转动接触.转动接触点的抗转动力矩mr=为颗粒间的抗转动系数).
1.2 数值模拟方案
本文离散单元模拟的材料为粗颗粒材料,其初始尺寸为0.3 m×0.3 m×0.6 m(长×宽×高),根据试样尺寸与颗粒的最大粒径比不应小于5 的原则[29],控制最大颗粒粒径dmax为60 mm.考虑DEM 的计算效率,试样最小粒径dmin设定为10 mm.有关研究表明粗粒料的级配可以用分形分布的函数来描述[30]
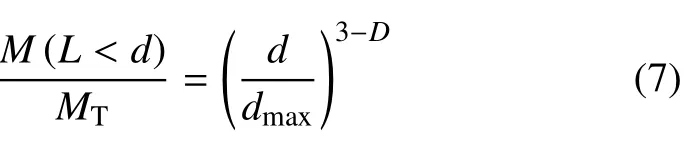
式中,d为颗粒的粒径;dmax为最大粒径;M(L<d)为小于粒径d的土体质量;MT为土体总质量;D为分形维数.对于最大粒径在60 mm 以内的粗粒料,D=1.88~2.63 为级配良好区间[30],因此本文数值试样级配的分形维数D=1.9.
在制备试样时,首先在模型尺寸范围内随机生成粒径服从图2(a) 所示分形分布的球体颗粒,数量为13 584,然后采用等向压缩的方法固结至目标围压,在等向压缩的过程中可以通过控制颗粒间滑动摩擦系数μs生成不同初始孔隙比的试样.图2(b)给出了在不同滑动摩擦系数μs下等向固结至200 kPa时试样孔隙比e的变化规律,发现孔隙比e随着μs的增大而增大,且增大幅度逐渐减小.在试样从固结状态的不同μs值变成μs=0.3 的稳定状态中,对于固结过程采用μs>0.3 的试样其孔隙比会降低,而对于固结过程采用μs<0.3 的试样其孔隙比保持不变.这种孔隙比降低的现象是由于减小滑动摩擦系数导致了颗粒间容许最大切向接触力μsfn的减小,造成了更多颗粒接触间的滑移,突然释放的剪切弹簧中的应变能转化为动能驱动颗粒重排,最终形成一个新的稳定结构.
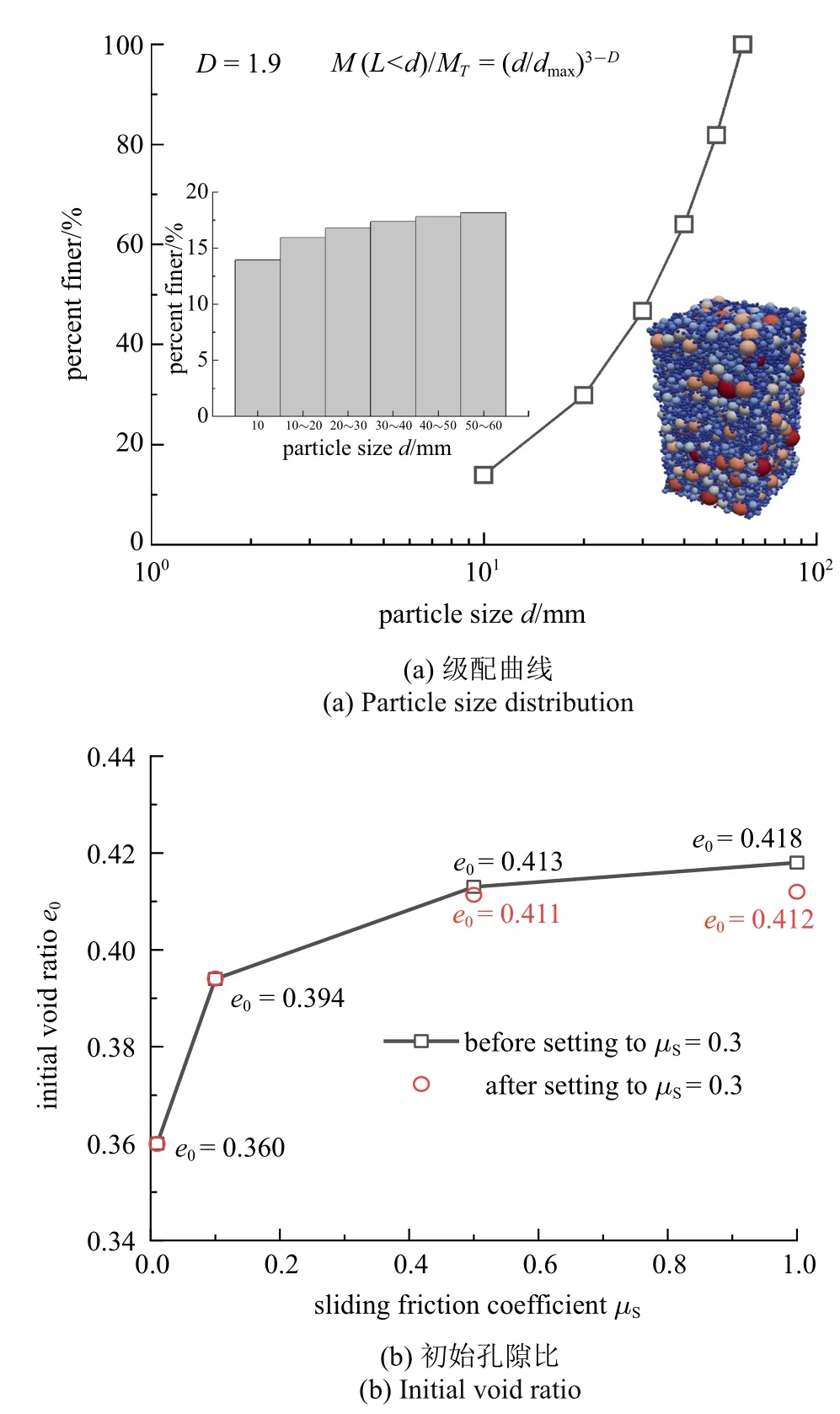
图2 DEM 数值试样级配与初始孔隙比Fig.2 Particle size distribution and initial void ratio of DEM specimen
本文在等向压缩至预定围压值200 kPa 的过程中设定μs=1.0,μr=0.0,采用周期性边界的伺服机制,制备得到相对密实度较低、边界效应较小的试样.本文的主要目的是研究剪切过程中的宏细观力学特性而非重现室内试验过程,因此在保证宏观力学规律合理的前提下,通过试算得到模拟中细观参数取值见表1,其中弹性模量与Guo[31]和Yan 等[32]的取值在同一数量级,刚度比取为1.0[33-34],在准静态加载情况下局部阻尼系数取为0.0[35].粒间抗转动系数μr取为0.0,0.01,0.05,0.1,0.15,0.2,共进行6 组数值模拟试验.

表1 剪切过程DEM 计算参数Table 1 Input DEM simulation parameters
2 颗粒体系的接触网络及表征方法
根据颗粒间的接触特性,如接触点的滑动与否、转动与否和强弱力情况,可以定义不同的子接触网络k,其中k可以代表非滑动(ns)、滑动(s) 或非滑动-非滚动(ns-nr) 子接触网络等.图3 为摩擦系数μs=0.3,μr=0.05 的试样在轴向应变ε1=25.0%时颗粒体系的全局接触网络和不同子接触网络的力链图.
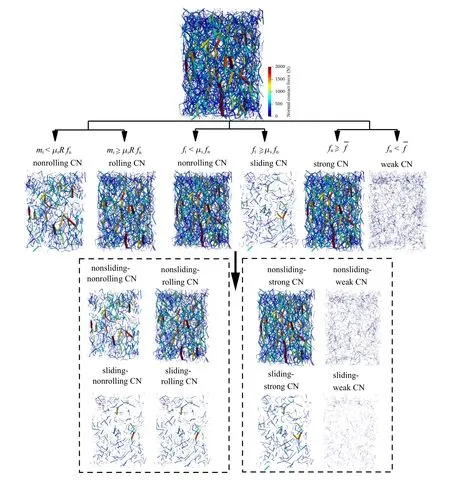
图3 颗粒接触网络分类方法Fig.3 Classification of contact networks(CNs)
为了定量表征不同子接触网络k的各向异性,一般用接触法向n和枝向量b的分布特征描述颗粒材料的几何各向异性,法向接触力fn和切向接触力ft的分布特征描述颗粒材料的力学各向异性.Oda[20]建议采用接触法向来表征全局组构张量φi j,定义为
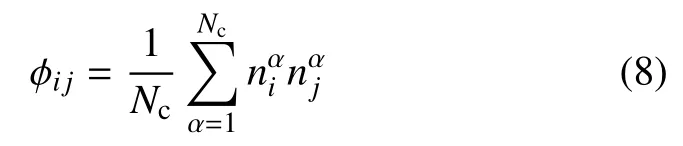
子接触网络k的各向异性参数可以根据接触法向、枝向量、法向接触力和切向接触力的各向异性二阶张量表示
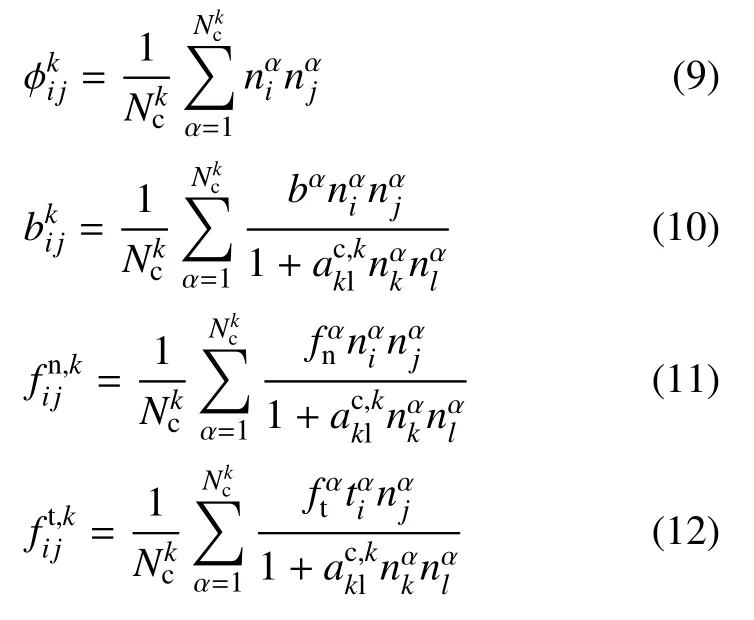
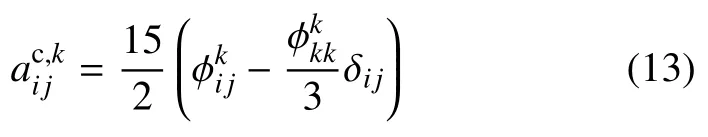
表征子接触网络k中枝向量、法向接触力和切向接触力各向异性程度的二阶偏张量可分别由下式进行计算

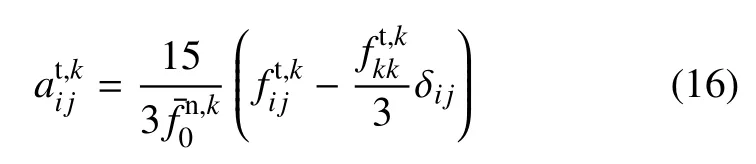
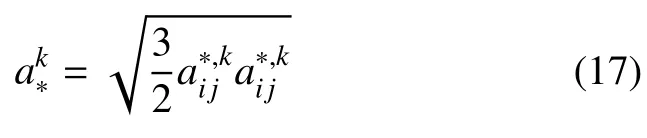
3 组构各向异性演变规律
3.1 子接触网络组构张量演变规律
图4 给出了摩擦系数μs=0.3,μr=0.05 的试样在剪切过程中全局组构张量φij和滑动、非滑动两种子接触网络的组构张量变化规律,以及轴向应变ε1=25% 时颗粒接触点数按接触角的空间分布玫瑰图.不同虚线表示全局组构张量φij在剪切过程中的变化,可以发现在ε1=0% 时,系统的组构φ11=φ22=φ33=0.33,表明试样此时处于各向同性阶段;随着轴向应变增大,大主应力方向组构φ11先增大,之后随着加载过程稍微减小并最终趋于一个相对稳定的状态;相应地,中主应力方向φ22和小主应力方向φ33先减小,之后稍微增大并保持相对稳定.对于滑动、非滑动两种子接触网络,非滑动接触的各向异性明显,主要沿大主应力方向集中,滑动接触在残余状态时各向异性较小,沿小主应力方向有轻微的集中.
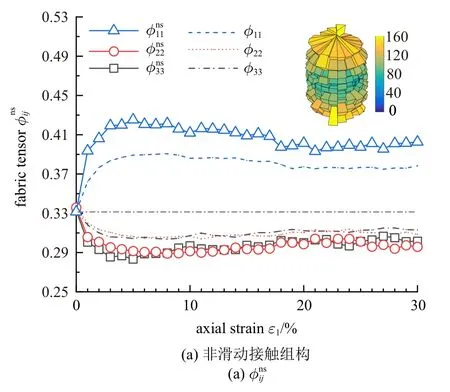
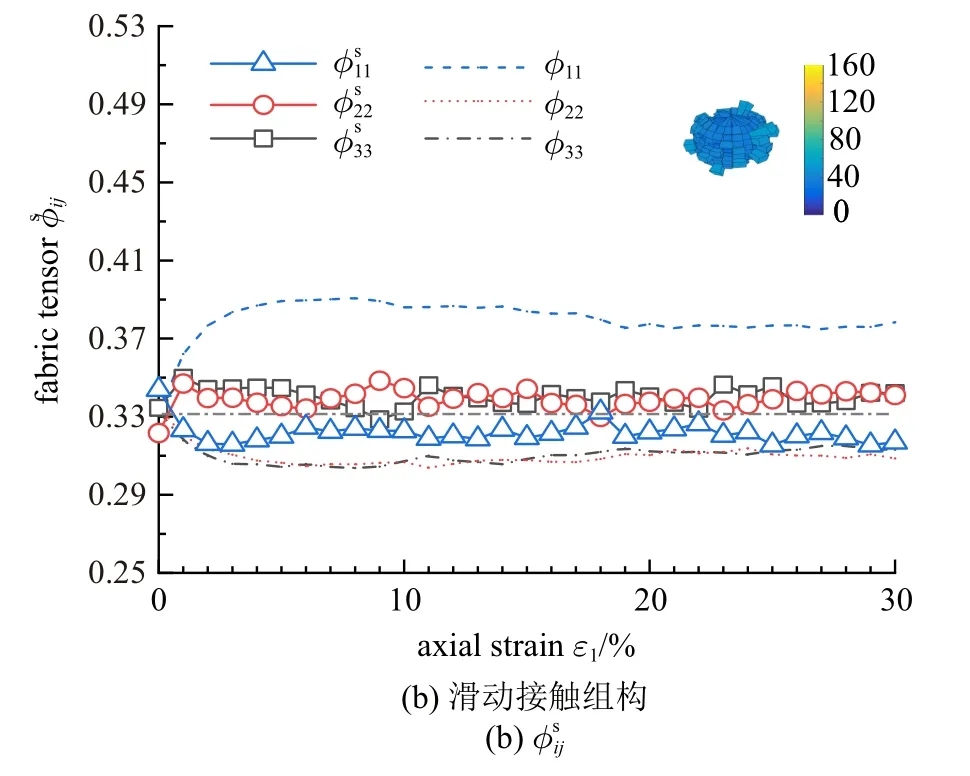
图4 滑动、非滑动接触的组构张量演变规律Fig.4 Evolution of fabric tensor of non-sliding and sliding contact networks
考虑到颗粒的抗转动特性,将接触网络进一步划分为非滑动-非转动、非滑动-转动(ns-r)、滑动-非转动(s-nr)和滑动-转动(s-r)4 种子接触网络,图5 给出了这4 种子接触网络的组构张量变化规律,发现:
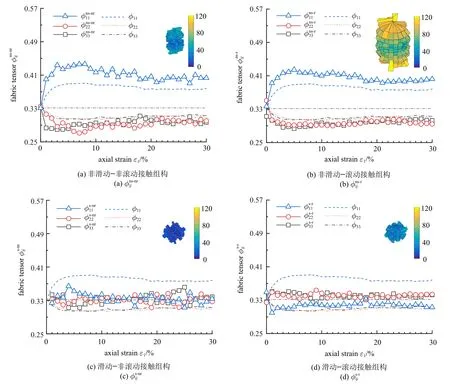
图5 非滑动-滑动-非转动-转动接触的组构张量演变规律Fig.5 Evolution of fabric tensor of the nonsliding-sliding-nonrolling-rolling contact neworks
(3)与转动、非转动接触的相关组构张量的变化不是独立的,受到颗粒间是否滑动的影响,剪切过程中系统的应力诱发各向异性主要是由非滑动接触引起的.
研究发现,接触网络中的强接触和弱接触对系统的力学作用机制完全不同,强接触对宏观力学贡献有决定性的影响.图6 给出了剪切过程中强、弱接触网络的组构张量演变规律,发现强接触sf 的数量小于弱接触wf 的数量,强接触sf 表现出大于整体的各向异性,且沿竖向集中,弱接触wf 在残余状态时各向异性不明显,沿大主应力方向有很小的集中.该现象与文献[3]的结论一致,证实了强接触形成柱状结构承担外部载荷,并由较多的弱接触沿四周支撑.

图6 强、弱接触的组构张量演变规律Fig.6 Evolution of fabric tensor of strong force and weak force contact networks
进一步地,当接触网络划分为非滑动-强接触(ns-sf)、非滑动-弱接触(ns-wf)、滑动-强接触(ssf)、滑动-弱接触(s-wf) 时,4 种子接触网络的组构变化有较大地差异(图7),发现非滑动-强接触(图7(a)) 的组构各向异性最明显,非滑动-弱接触(图7(b)) 和滑动-强接触(图7(c)) 的组构与系统组构的大小相差不大,该3 种接触均沿大主应力方向集中,而滑动-弱接触(图7(d))沿小主应力方向有轻微的集中.
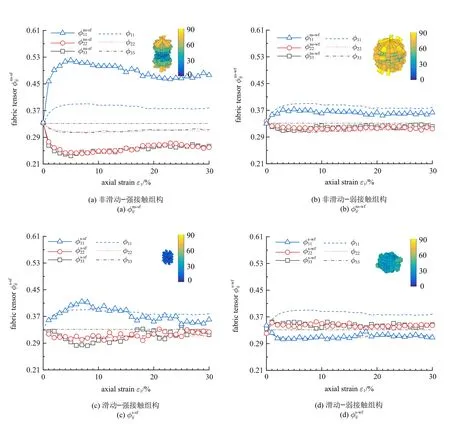
图7 非滑动-滑动-强-弱接触的组构张量演变规律Fig.7 Evolution of fabric tensor of nonsliding-sliding-strong-weak contact networks
3.2 抗转动特性对各向异性参数的影响
基于不同子接触网络的各向异性指标可以用来分析颗粒体系的细观力学机理.图8 分别给出了摩擦系数μs=0.3,μr=0.05 的试样在剪切过程中不同子接触网络k的接触法向各向异性参数和法向接触力各向异性参数的演变规律,从图8(a)可以看出非滑动、强接触和非滑动-强接触网络的均大于全局接触法向各向异性ac,其中强接触(特别是非滑动-强接触)是几何各向异性的主要贡献者,该规律与本文第2 节组构张量的演变规律一致.图8(b)显示全局的接触法向力各向异性an最大,这是因为子接触网络仅可以从有限的接触法向力中进行选择,该结果与文献[25]的模拟结果一致.
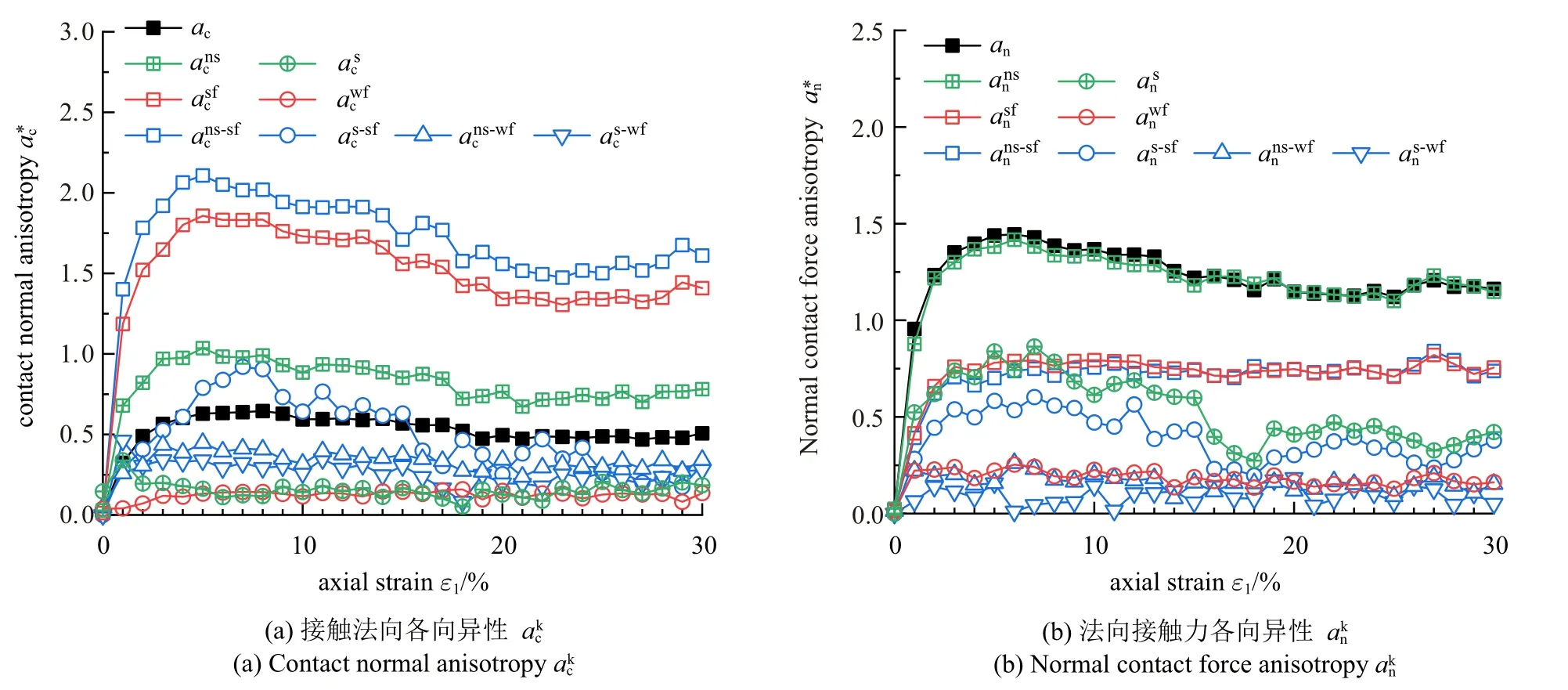
图8 剪切过程中子接触网络的各向异性演变规律Fig.8 Evolution of anisotropy indexes of sub-contact networks during shearing
图9 选取了对各向异性贡献较大的3 个子接触网络(ns,sf,ns-sf) 和全局接触网络,研究抗转动效应对四种接触网络的各向异性参数的影响规律,发现:
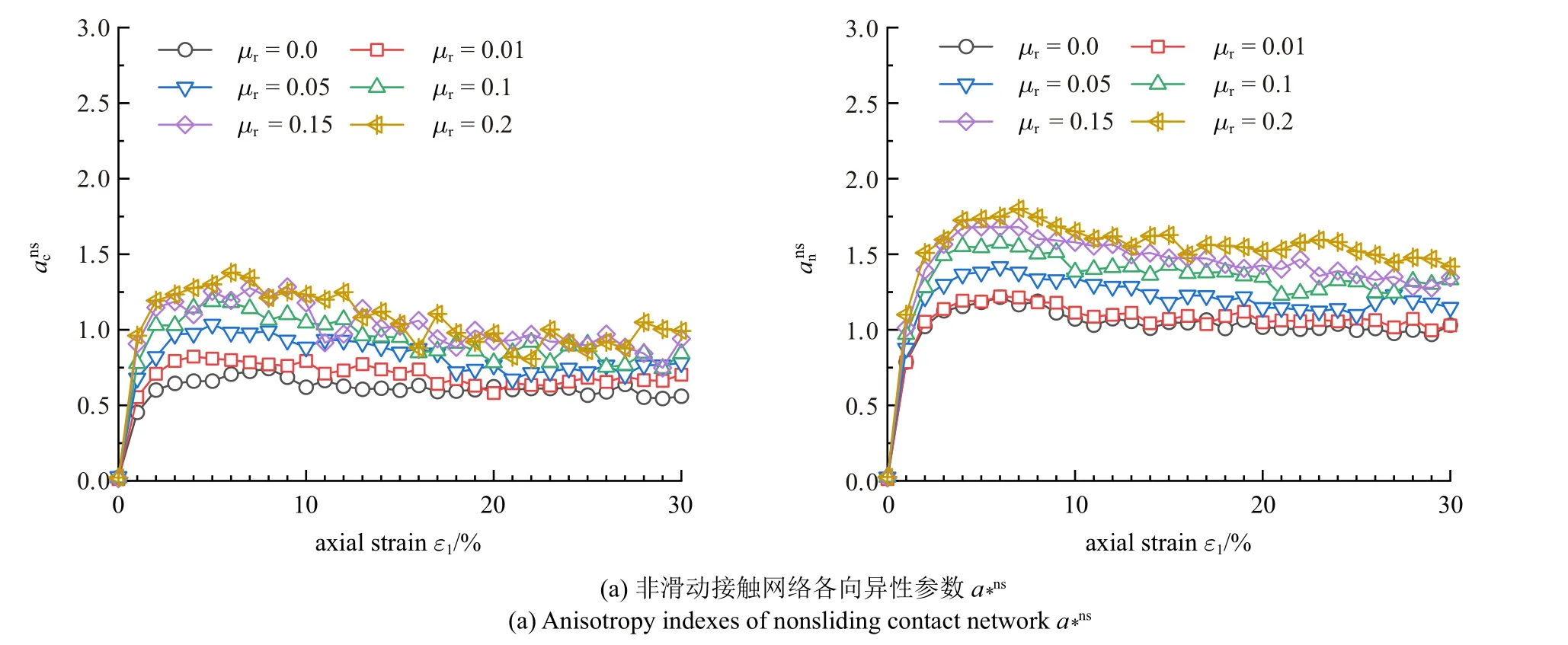
图9 抗转动系数对不同接触网络各向异性指标演变规律的影响Fig.9 Influence of rolling resistance on the evolution of anisotropy indexes of different contact networks
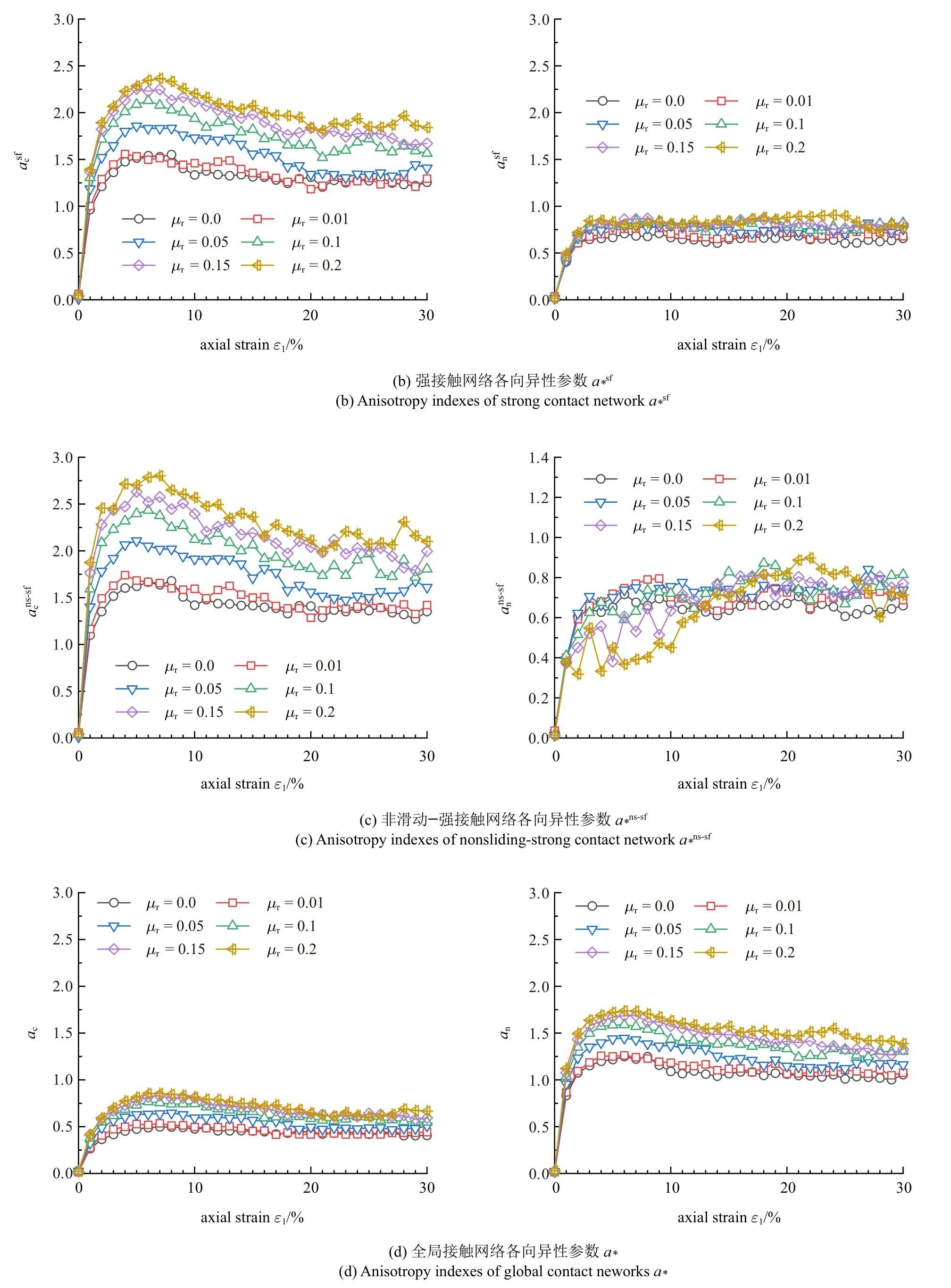
图9 抗转动系数对不同接触网络各向异性指标演变规律的影响(续)Fig.9 Influence of rolling resistance on the evolution of anisotropy indexes of different contact networks(continued)
4 应力-接触力-组构关系
Christonffersen 等[37]提出了基于全局接触网络的颗粒体系应力张量
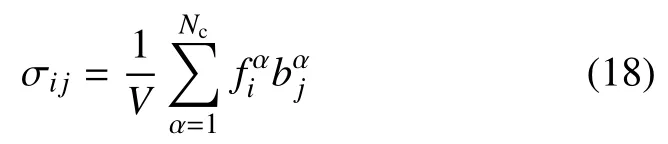
式中,V为颗粒体系总体积;为接触点c处的法向接触力;为接触点c处的枝向量;Nc为颗粒体系的总接触点数.系统的平均有效应力p,广义剪应力q,不同方向主应变εi(i=1,2,3)和体应变εv分别由下式进行计算

式中,li0是剪切开始时试样不同方向的初始长度,li是剪切过程中试样不同方向的长度.
图10 给出了剪切过程中应力应变变化规律,可以看出,应力比出现较为明显的峰值,并随抗转动系数μr的增大而增大,对体应变的影响也较为明显,剪胀性增大.

图10 不同抗转动系数下宏观应力-应变关系曲线Fig.10 Curves of macro stress-strain relationship under different rolling friction coefficients
Ouadfel 等[22]与Li 等[38]针对全局接触推导了应力-接触力-组构(stress-force-fabric,SFF)关系,当进一步将全局接触分为不同接触网络时,Sufian 等[25]推导了在若干子接触网络中的SFF 关系,全局偏应力比q/p*可以表示为子接触体系中不同各向异性参数的函数
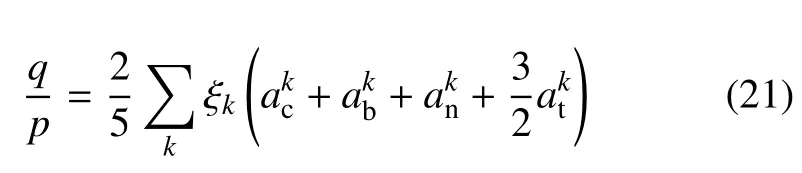

式中,ζk=Nk/N是子接触网络k中接触数目Nk占整个体系接触数N的比例,γk=是子接触网络的平均法向接触力与体系平均法向接触力之比.
图11 给出了抗转动效应对不同子接触网络ξk的影响规律,发现非滑动和非滑动强接触网络的ξns和ξns-sf随着抗转动系数μr的增大而减小,说明提高抗转动效应会减小接触数目和平均法向接触力的贡献程度;而强接触网络的ξsf不随抗转动系数的改变而改变,说明强接触网络对宏观应力的贡献程度在不同μr情况下均相同.
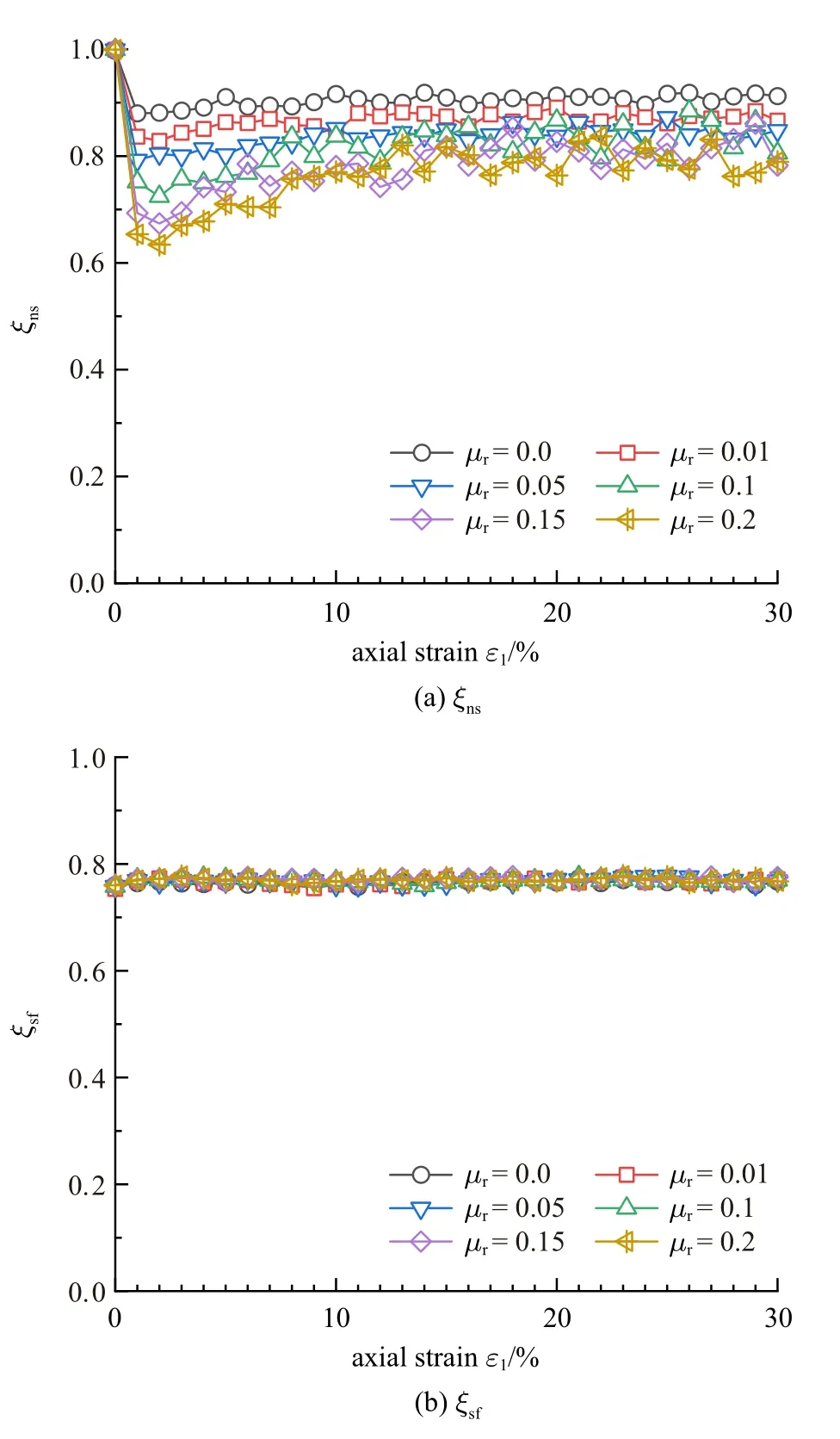
图11 抗转动系数对ξk 的影响规律Fig.11 Influence of rolling resistance on ξk
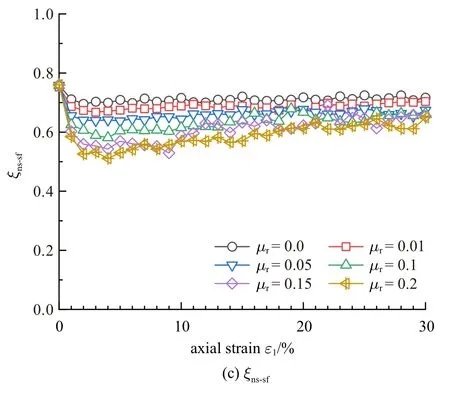
图11 抗转动系数对ξk 的影响规律(续)Fig.11 Influence of rolling resistance on ξk (continued)
图12 对比了由SFF 关系得到的ns-s-sf-wf 接触网络应力比q/p*与由式(19) 计算的应力比q/p,可以看出,对于采用不同抗转动系数的颗粒体系,SFF的理论预测值与实际的应力比非常接近,从而表明了SFF 理论的适用性.

图12 SFF 理论应力比验证Fig.12 Validation of SFF relationship
5 结论
本文采用离散单元法模拟了不同抗转动系数μr情况下颗粒材料三轴剪切试验,根据接触点的滑动与否、转动与否和强弱力情况,将颗粒体系分为不同的子接触网络,分析了剪切过程中不同子接触网络的组构张量的演变规律,并通过统计不同子接触网络的各向异性参数,研究了抗转动效应对各向异性演变规律的影响,主要结论有:
(1) 分析了剪切过程中非滑动-滑动-非转动-转动4 种子接触网络的组构张量变化规律,发现转动、非转动接触的组构变化不是独立的,受到颗粒间是否滑动的影响,剪切过程中系统的应力诱发各向异性主要是由非滑动接触引起的.
(2)剪切过程中非滑动接触的各向异性明显,主要沿大主应力方向集中,滑动接触在残余状态时各向异性较小,沿小主应力方向有轻微的集中;强接触表现出大于整体的各向异性,且沿竖向集中,弱接触在残余状态时各向异性不明显,沿大主应力方向有很小的集中.
(3)通过分析抗转动效应对不同子接触网络的各向异性参数影响,发现提高抗转动效应会导致组构各向异性的增大,并提高接触网络的稳定性.非滑动接触网络和全局网络的法向接触力各向异性和an均随抗转动系数μr的增大而增大,且法向接触力各向异性比接触法向各向异性大;而与强接触相关的子接触网络的法向接触力各向异性和变化不大,且接触法向各向异性占主导地位.
(4)非滑动和非滑动-强接触网络的ξns和ξns-sf均随着抗转动系数μr的增大而减小,说明提高抗转动效应会减小接触数目和平均法向接触力对宏观应力的贡献程度;而强接触网络的ξsf不随抗转动系数的改变而改变,说明强接触网络对宏观应力的贡献程度在不同μr情况下均相同.

