基于组合神经网络的雷诺平均湍流模型多次修正方法1)

张 珍 叶舒然 岳杰顺 王一伟,2) 黄晨光,**

*(中国科学院力学研究所流固耦合系统力学重点实验室,北京 100190)

†(中国科学院大学工程科学学院,北京 100049)

**(中国科学院合肥物质科学研究院,合肥 230031)

引言

当前,求解雷诺平均(Reynolds-averaged Navier-Stokes,RANS)方程仍然是解决工程问题相对切实可行且有效的手段[1-7].但由于RANS 方程中所使用的涡黏模型往往假设雷诺应力和平均应变率张量之间满足线性关系[8],难以充分捕捉流场中存在的各向异性特征,导致对许多未充分发展的湍流流动的预测,例如三维分离流、强压力梯度流、两相流是不准确的[9-14].针对这些问题,一些学者提出了高阶涡黏模型,在一定程度上能够提高RANS 方程的预测精度[15-16],然而由于高阶模型中的参数表达不够清晰,并且计算收敛性差,使得这类模型未被广泛应用.

近年来,随着人工智能的发展,机器学习算法在湍流建模中得到了越来越多的应用[17-39].其中,深度学习技术非常适合于提取湍流的多尺度特征,并且平移、旋转和其他不变性在深度学习体系结构中很容易实现.在这类工作中,机器学习可以直接用作黑盒工具,也可以与现有模型结合使用,以提升模拟的精度.Xie 等[17]对人工神经网络在湍流亚格子模型中的研究进展进行了总结性介绍,并讨论了基于不同网络模型重构新的亚格子模型.Brunton 等[18]、Brenner等[19]以及Duraisamy 等[20]也阐述了机器学习算法在RANS 闭合模型中应用的研究进展,表明了数据驱动RANS 建模具有一定的研究深度和广度.

在数据驱动RANS 湍流建模的研究中,Ling等[21]构建了一种嵌入伽利略不变性的张量基网络体系结构,其预测的雷诺应力更加贴近湍流的物理性质,显示出了神经网络结合伽利略不变性在对具有高维非线性特征的数据进行建模的优良性能.之后,一些学者在构造RANS 闭合模型时,也采用了类似的策略以保证伽利略不变性,并应用到不同类型的流动(如槽道流、后台阶、周期山状等流动)中进行流场预测[22-30],其预测结果相比原始RANS 模型均有所提升.在这些研究中,主要是利用机器学习算法获得改进的雷诺应力的本构关系,完全显式的取代RANS 求解器中的雷诺应力,而动量方程和输运方程中的其他项则保留不变.此外,Zhang 等[40]以及Parish 等[41]从另一个方面出发,用机器学习优化输运方程中的系数,而雷诺应力本构关系未被修正.

尽管上述修正模型的预测性能已被证明得到了提升,但对后验流场的预测精度仍有提升的空间.根据Wu 等[42]的研究,即显式数据驱动雷诺应力模型会导致条件数非常大,从而很难用局部信息准确地预测全局最优点位置.鉴于此,Beetham 等[43]将RANS模型分为线性部分和非线性部分,线性部分保持传统RANS 方法隐式求解,非线性部分基于人工神经网络训练预测.由于线性部分对雷诺应力影响很大,因此仅使用神经网络更新雷诺应力的非线性部分对流场预测的精度仍不够.

因此本文建立了一种基于组合神经网络的修正方法,针对涡黏模型的线性部分,利用全连接神经网络对涡黏系数进行预测以实现隐式求解;对于非线性部分,基于高阶涡黏框架,使用张量基神经网络进行预测;获得的两部分之和为雷诺应力的最终预测结果.最后为了实现后验速度场的精度闭环,对RANS 湍流模型实施了多次修正策略.模型训练和修正阶段所使用的数据为不同坡度的周期山状流的模拟结果.

1 RANS 涡黏模型

不可压缩的Navier–Stokes(NS)方程为

式中,ui为瞬时速度的第i个分量,p为瞬时压强,ρ为密度,ν 为运动黏度.

对NS 方程进行时间平均可以得到不可压缩的RANS 方程

由式(3) 和式(4) 可以看出,相比于原始NS 方程,RANS 方程出现一个多余项,即雷诺应力因此需要引入其与平均流场之间的关系才能使得RANS方程封闭.目前k-ε 模型和k-ω 模型是使用最广泛的涡黏模型,这些模型基于Boussinesq 假设雷诺应力与平均应变率张量之间满足线性关系.雷诺应力为对称张量,可以分解为各向同性和各向异性部分,分解结果如下

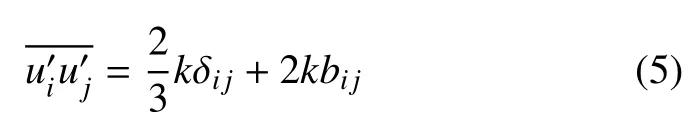
式中,k为湍动能,δij为Kronecker 符号,2kδij/3 为各向同性部分,bij为无量纲各向异性雷诺应力.

目前广泛使用的线性模型难以捕捉到流场中存在的许多各向异性,因此一些学者提出了一些非线性涡黏模型,例如Pope[15]提出的有效黏度模型.该模型从平均应变率张量和平均旋转率张量导出高阶张量,以便更准确地对雷诺应力建模,最后得到各向异性雷诺应力的本构关系的一般形式为

式中,ε 为湍流耗散率.

由于上述非线性涡黏模型的基张量的标量系数G的具体表达式不易获得,并且该模型并不总能提高预测性能,反而往往会降低收敛性[44],因此,该模型尚未得到广泛应用.但随着深度学习技术在流体力学中的应用,可以借助人工神经网络,实现对基张量Tij的标量系数G建模,进而得到各向异性雷诺应力bij.在二维流场中,重构的各向异性雷诺应力的本构方程只需要以下4 个基张量[45],即

其中,公式右侧第1 项为线性部分,其余3 项为非线性部分.

2 RANS 湍流模型修正

2.1 基于组合神经网络的RANS 湍流模型修正方法

基于组合神经网络的RANS 湍流模型修正预测的示意图如图1 所示,其中神经网络1 的输出结果为涡黏系数(eddy viscosity neural network,EVNN) νt;神经网络2 为张量基神经网络(tensor basis neural network,TBNN),其输出结果为各向异性雷诺应力bij.两个人工神经网络分别对应如下的回归函数,即f1:{λ1,λ2}→νt和f2:{λ1,λ2}→bi j.

图1 基于组合神经网络的RANS 湍流模型修正框架图Fig.1 Framework of modification for RANS turbulence model based on combined neural network

使用壁面解析的LES 方法获得高保真数据作为神经网络的输出结果,使用RANS 模拟获得基线数据作为神经网络的输入特征以及基张量基于上述数据对两个神经网络分别进行训练,得到回归关系f1和f2,并使用训练好的模型对原始RANS 模拟的一个新流场进行修正预测.具体的修正计算分为以下3 个主要步骤:

(1)修正计算时,新流场模拟得到的输入特征被作用于回归函数f1获得修正流场中的,进而得到修正流场中雷诺应力的线性表达

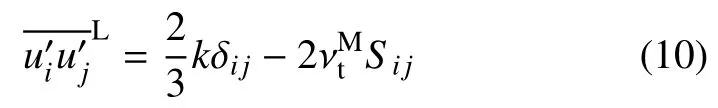
(2)同样地,一个新的流场被用来获得输入特征和基张量,使用训练好的回归数f2来获得修正流场中的各向异性雷诺应力

进而由式(5)可以得到修正流场中的雷诺应力,并取其非线性项

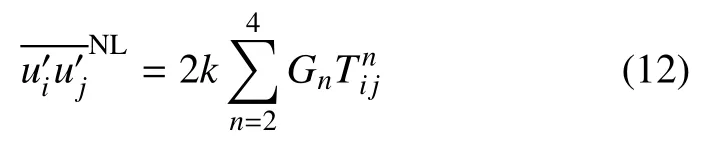
(3) 由式(10) 雷诺应力的线性部分与式(12) 雷诺应力的非线性部分相加得到雷诺应力之和

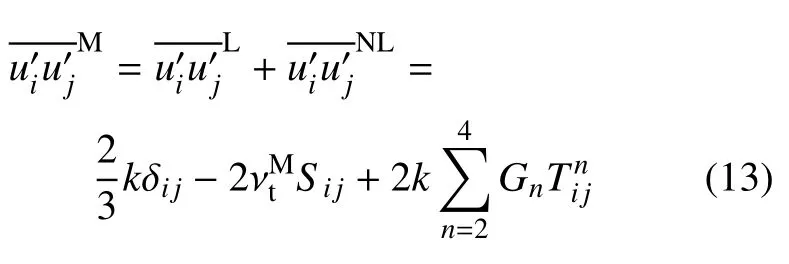
用来迭代更新RANS 框架中的动量方程和输运方程.

2.2 RANS 湍流模型的多次修正方法

基于组合神经网络对RANS 模型进行修正可以提高后验流场的预测精度,如果对后验流场进行特征提取并作为神经网络的输入重新进行模型的训练和修正,有可能进一步提升修正模型的预测精度.为此,采用了如图2 所示的多次修正的方法.相比于图1,增加了红色箭头指示的内容,具体实现流程如下:

图2 RANS 湍流模型多次修正框架图Fig.2 Framework of multiple modifications for RANS turbulence model

(1) 基于初始先验流场数据对神经网络进行训练,并用训练好的模型初次修正先验流场(priori flow,prf),得到后验流场1(posterior flow 1,pof 1);

(3)如果pof 1 未达到预测精度,修正结果将被反馈给组合神经网络进行下一次训练,训练好的模型将用于对先验流场prf 进行下一次修正,得到后验流场pof 2;

(4) 如果pof 2 达到预测精度,则重复步骤2,反之重复步骤3.通过多次修正,最终后验流场达到高保真数据精度即为实现精度闭环;

(5)实现精度闭环后,基于最终训练的神经网络直接用于一个新的流场进行修正预测,以验证方法的鲁棒性.

本文中建立的RANS 模型修正方法,相比于显式数据驱动RANS 建模方法的优势有:

(1)基于组合神经网络的RANS 修正模型同时对雷诺应力的线性部分和非线性部分进行修正,可提升预测精度;通过隐式处理保证数值稳定性.

由此可见，规范化、常态化的医务志愿者服务发展策略，不仅有利于改善医院就医环境，提高医院服务质量，也有利于营造良好的社会健康服务氛围，促进卫生事业发展。

(2)实施多次训练修正的策略可实现从修正计算到神经网络训练过程的反馈,最终达到后验流场的精度闭环.

2.3 神经网络结构与参数

本文所使用的TBNN 和EVNN 的结构框架分别如图3(a)和图3(b)所示,参数设置见表1,隐藏层的激活函数均为Leaky ReLU[46]

表1 神经网络参数Table 1 Neural network parameters

图3 神经网络结构图Fig.3 Schematic of the neural network

TBNN 和EVNN 的损失函数分别为

式中,下角标TBNN 和LES 分别代表神经网络经过训练以后输出的结果和真实高保真结果,N代表当前数据集的数量.并采用梯度下降法调整参数权重的大小来最优化模型结果,学习率伴随网络训练步长进行变化.另外,为了避免神经网络过拟合问题,在损失函数中加入了正则化[47].

3 数值模拟结果

为了验证本文所提出方法的优势和性能,采用了被广泛用于测试案例的周期山状流[48-51]进行神经网络的训练及RANS 模型的修正.通过与Breuer 等[48]的LES 结果、显式数据驱动模型以及原始RANS 结果进行比较,分别分析了修正模型在速度场、壁面平均压力系数和平均摩擦力系数的预测结果.

3.1 算例设置

计算域的原始几何如图4 中的黑色边界所示,其中流向的计算域为Lx=9.0h(两个山峰之间的距离),且流向计算域的平坦部分长5.142h,山坡两侧总长3.858h;法向最大计算域为Ly=3.035h;展向的计算域为Lz=4.5h,h为山的高度.对于周期山状流,当坡度变大时,即山坡与水平位置的夹角变大,流动分离特征更强,传统RANS 模型相比于LES 方法的预测能力更加有限且迫切需要改进.因此,本文利用Breuer 等[48]采用的壁面解析的LES 方法模拟同一雷诺数下具有不同坡度的周期山状流获得目标数据,其中,时间格式采用一阶隐式欧拉格式,梯度格式采用二阶高斯-格林积分法,散度格式采用二阶迎风格式,拉普拉斯项格式采用带非正交修正的高斯格林积分方法.而基线数据则由RANS 方法中k-ε 模型获得.进一步,基于大坡度的流动进行模型训练以实现对小坡度流动的修正.

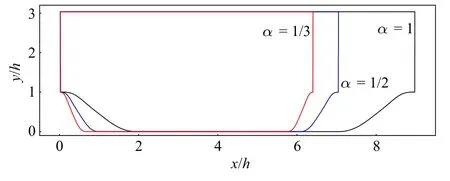
图4 3 种几何外形的计算域分布Fig.4 Computational domain of three geometric

文中通过对原始山坡两侧的流向长度设置缩放因子获得不同坡度结构的周期山状流,保证流向计算域的平坦部分长度恒定,因此计算域的水平总长度为x/h=3.858 α+5.142,其中α 为缩放因子.周期山状流的雷诺数Re=Ubh/ν=10 595,其中,Ub为整体流动的平均速度.流向方向以及展向方向均设置为周期性边界条件,因此平均流动可被认为二维流动.

不同坡度算例在两种计算方法下的网格设置如表2,LES 方法对三维流场进行模拟,RANS 则是针对二维流场进行模拟.计算得到的LES 数据经过展向平均后,再通过插值对应到粗网格下的二维RANS数据.

表2 模拟所用的网格单元Table 2 Grid cells of simulations performed

计算得到的LES 数据中提供了脉动速度的平均二阶相关张量,根据定义可知该张量为LES 网格下的雷诺应力场进一步可以得到湍动能以及无量纲后的各向异性雷诺应力张量分别为

在EVNN 框架训练时,LES 数据中需要有对应于RANS 模型涡黏系数的量,即真值νt.基于Boussinesq 假设可知雷诺应力和涡黏性系数之间满足如下关系

由式(18)和式(19)得出在Boussinesq 假设下

因此,可以通过将各向异性应力张量bij投影到应变率张量Sij上来计算-νt/k,即

式中,bijSij表示张量的双点积,表示矩阵Sij的Frobenius 范数.最终可求得真值νt

真值νt的4 个不同垂直位置处的剖面分布如图5 所示,可以看出,剖面曲线为连续光滑分布,可用于对EVNN 进行训练.

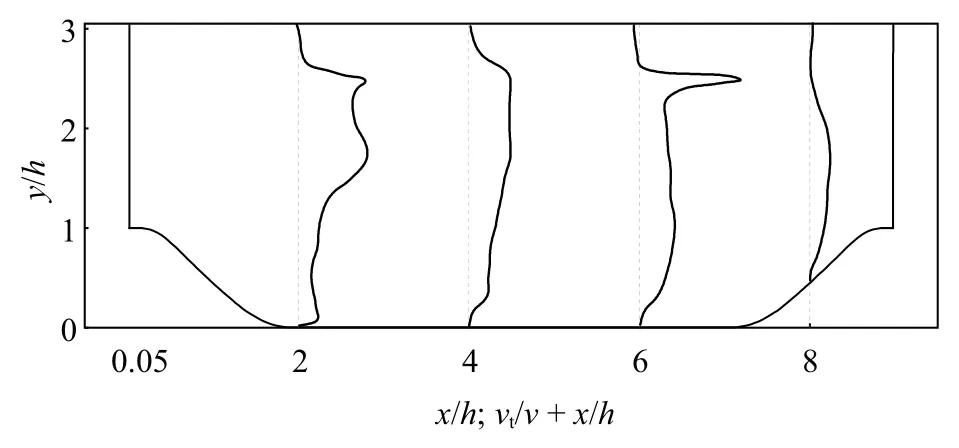
图5 LES 模拟的涡黏系数: x/h=2,4,6,8Fig.5 Eddy viscosity simulated by LES at x/h=2,4,6,8

3.2 数据验证

图6 给出了由LES 模拟获得的α=1 时的周期性山状流的二阶脉动统计量的剖面分布图,即正应力分量和切应力分量并与Breuer等[48]进行对比,可以发现两者在趋势和大小上都彼此吻合.由此验证了该模拟方法的有效性,并基于该方法对α=1/2 和1/3 进行数值计算.

图6 LES 预测的x/h=2,4,6 处的应力剖面结果(Re=10 595),并与文献[48]的结果进行对比Fig.6 Predicted stress profiles by LES at x/h=2,4,6(Re=10 595),and compared with the results of Ref.[48]

3.3 预测结果

3.3.1 组合神经网络预测结果

用于模型训练和预测的算例如表3 所示,坡度α为1/2 和1/3 的两个流场被用于模型的训练,训练好的模型用于修正α=1 的周期山状流.

表3 用于模型训练和修正的算例Table 3 Cases for model training and modification

周期山状流不同的剖面位置被用来定量对比LES 方法、RANS 修正模型以及原始RANSk-ε模型的预测性能.其中x/h=2.0 为回流区的中心,x/h=4.0 位于再附点位置的附近,x/h=6.0 为再附着后的流动位置.无量纲的平均流向速度(Ux/Ub)剖面的预测结果如图7 所示,其中红色线条代表本文建立的RANS 修正模型的预测结果,而粉色线条是参考Ling 等[21]提出的基于TBNN 的显式雷诺应力修正模型的预测结果.可以发现,显式模型相对原始RANS 模型的预测性能并没有显著提高,尤其是对回流区大小以及再附点位置的捕捉,该结果验证了直接将神经网络获得的新的雷诺应力本构关系完全显式替代原始雷诺应力的方法确实会造成RANS 求解器的非物理震荡以及数值不稳定性.而本文所用的基于组合神经网络的修正模型对速度场的预测精度远优于原始RANS 模型,且对回流区大小以及再附流动的预测与LES 结果较为接近.这证明了将RANS模型分为线性部分(通过EVNN 预测更新黏性项以隐式求解)和非线性部分(通过TBNN 预测雷诺应力仅更新非线性项) 提高了RANS 求解器的稳定性和涡黏系数的准确性.

图7 周期山状流不同位置处的平均流向速度剖面预测Fig.7 Prediction of the mean streamwise velocity profiles at different locations after one loop modification

为了进一步验证基于组合神经网络的修正模型的预测性能,对比了LES 方法以及原始RANS 模型对下壁面平均压力系数和平均摩擦力系数的分布预测,结果如图8 所示.由图8(a)中的平均压力系数可以看出,修正模型可以捕捉到与LES 一致的变化趋势,但对压力系数捕捉的精度仍低于LES 结果.而对比图8(b)关于平均摩擦力系数的预测结果可以发现,修正模型的预测结果与LES 结果更为吻合,特别是可以准确捕捉到再附点的位置(图中绿色横线标注),然而修正模型对摩擦力峰值的捕捉精度仍不够准确.

图8 周期山状流的平均压力系数分布和平均摩擦力系数分布Fig.8 Prediction of the mean pressure coefficient and the mean friction coefficient after one loop modification

3.3.2 多次修正预测结果

为了实现修正模型对流场预测的精度闭环,采用了多次修正的策略.本文基于组合神经网络对RANS模型进行了3 次训练修正计算,并基于最终神经网络对RANS 模拟的一个新的流场进行修正预测,具体的数据选择如下.

(1) 第1 次:基于先验流场(α=1/3,1/2) 构建输入,第1 次训练神经网络,然后对先验流场(α=1/3,1/2)进行修正,得到后验流场1;

(2)第2 次:基于后验流场1 的数据构建输入,第2 次训练网络,之后重新对先验流场(α=1/3,1/2)进行修正,得到后验流场2;

(3)第3 次:基于后验流场2 的数据构建输入,第3 次训练网络,进而再次对先验流场(α=1/3,1/2)进行修正,得到最终的修正流场;

(4)基于第3 次获得的神经网络模型对RANS 模拟的一个新流场(α=1)直接进行修正预测.

在计算过程中,雷诺应力被进行迭代更新.图9是基于组合神经网络对原始RANS 模型进行3 次训练与修正计算的平均流向速度剖面结果.从图中可以看出,修正模型对速度场的预测精度和LES 结果一致,进一步地,修正模型预测的下壁面的平均压力系数和平均摩擦力系数的分布也更加接近LES 结果(见图10).

图9 多次修正下周期山状流不同位置处的平均流向速度剖面预测Fig.9 Prediction of the mean streamwise velocity profiles at different locations after three loop modifications

图10 多次修正下周期山状流的平均压力系数分布和平均摩擦力系数分布Fig.10 Prediction of the mean pressure coefficient and the mean friction coefficient after three loop modifications

4 结论

机器学习算法结合传统RANS 模型的数据驱动模型是具有实际意义且可提高预测性能的一种方法,也可以改善RANS 湍流建模的差异.为了进一步增强数据驱动RANS 湍流模型的数值稳定性以及预测精度,本文发展了一种基于组合神经网络(TBNN 和EVNN)预测涡黏系数和雷诺应力各向异性张量的修正方法,使用EVNN 预测涡黏系数实现了雷诺应力线性部分的隐式求解,利用TBNN 预测雷诺应力的非线性部分提升了模型预测的精度.

基于组合神经网络对RANS 模型进行隐式修正相比于显式数据驱动模型抑制了模型的非物理震荡且提高了数值的稳定性.经过多次修正后的模型对后验速度场、平均压力分布和平均摩擦力分布的预测精度均更接近LES 结果,实现了对后验流场预测的精度闭环.

在下一步的工作中,需要进一步研究RANS 湍流模型的泛化性能以应用到更复杂的流动中.同时深度学习模型还存在一些普适性的难题,即难以解释输入数据与预测结果之间的因果关系,而且深度学习框架过分的依靠数据,可能会产生虚假的规律,可信度受到质疑,因此在未来考虑进一步放松数据需求,建立无监督的网络模型以及具有物理约束的收敛判据是非常重要的.