基于GIMT和弧长参数化的QG-Ball曲线近似合并
胡先智,梁 艳,吕 丹,胡 钢
基于GIMT和弧长参数化的QG-Ball曲线近似合并
胡先智1,梁 艳2,3,吕 丹4,胡 钢4
(1. 西安理工大学信息化管理处,陕西 西安 710048;2. 西安交通大学电子与信息工程学院,陕西 西安 710049;3. 西安思源学院理工学院,陕西 西安 710038;4. 西安理工大学理学院,陕西 西安 710054)
曲线近似合并作为CAGD中复杂曲线设计的一种有效技术,一直备受学者们的关注,并在CAD/CAM领域得到了广泛的应用。针对现有带形状参数的广义Ball曲线难以合并的问题,提出了一种基于广义逆矩阵理论(GIMT)和弧长参数化的QG-Ball曲线近似合并方法。首先,利用曲线近似弧长参数化算法计算出QG-Ball曲线弧长等分对应的配置点列(亦称等分点)和配置点参数值;其次,基于所得等弧长配置点列及其参数值,再结合广义逆矩阵理论和曲线拟合方法,便可以直接得到计算合并后QG-Ball曲线控制顶点的一个显式表达式;最后,利用连续函数的L2范数定义了一个度量曲线合并效果的误差计算公式,并给出了一些具有代表性的数值算例及其合并误差。实例结果表明,所提出的方法可以高效地实现QG-Ball曲线的近似合并,不仅易于操作、误差计算简单,而且能方便地推广到其他曲线的近似合并。
QG-Ball曲线;形状参数;近似合并;广义逆矩阵;弧长参数化
Ball曲线曲面是由Ball基函数构造的自由型参数曲线曲面,由于具有独特、优良的性质使其成为了CAD中表示曲线和曲面的最重要方法之一。1974年,英国数学家BALL[1]首次构造一种有理三次Ball曲线,并将其作为CONSU RF机身CAD造型系统的数学基础。Ball曲线有着与Bézier曲线类似的性质,如对称性、凸包性、端点插值性、几何不变性等。此外,相比Bézier曲线而言,广义Ball曲线还具有如下优点[2]:①在曲线递归求值以及升降阶的计算速度方面,明显优于Bézier曲线;②比Bézier曲线更适合曲线次数的提高;③Ball曲线退化为低一阶曲线的条件比Bézier曲线要简单、易判断。因此,Ball曲线曲面具有比Bézier曲线曲面更为广泛地应用价值,并受到了国内外学者的广泛关注[3-8]。
Ball模型在给定其控制顶点(或控制网格)后,其形状就被唯一确定了,若要修改自身形状则必须调整其控制顶点(或网格)。有理Ball方法通过引入权因子,不改变控制顶点(或控制网格),由权因子可调整曲线曲面形状。但是,有理Ball曲线曲面同样存在缺陷,如权因子如何选取、求导次数增加、求积分不方便等[9]。为了增强Ball方法的形状可调性和逼近性,文献[10-15]研究了推广的Ball曲线曲面,分别提出了含形状参数的广义Ball曲线曲面。其中,文献[15]构造的四次广义Ball曲线作为一种新颖的Ball曲线模型,其含有2个形状控制参数,具有较好的形状可调性。进一步,文献[16-17]分别研究了文献[15]中四次广义Ball曲线和曲面的分割算法。
然而,在CAD/CAM的系统中曲线的近似合并是经常遇到的棘手问题[18]。近似合并能够有效减少产品设计与开发中的数据传输量,使得数据传输与交换可以在不同的CAD/CAM系统中实现。曲线的近似合并作为CAGD领域一个重要的研究内容,多年来备受国内外学者关注,并在Bézier和B样条曲线曲面近似合并方面取得了一些研究成果[19-23]。令人遗憾的是,关于带形状参数的广义Ball曲线的近似合并问题却一直未被解决。为此,本文结合广义逆矩阵理论、近似弧长参数化及曲线拟合方法,研究了文献[15]中四次广义Ball曲线的近似合并问题,提出了该曲线的一种有效合并方法。
1 QG-Ball曲线的定义
定义1.给定4个平面或空间控制顶点向量(=0,1,2,3),对Î[0,1]和,Î[-2,4],定义的曲线称为带形状参数,的四次广义Ball (quartic generalized Ball,QG-Ball)曲线[1],(简称为QG-Ball曲线)为
其中,四次广义Ball基函数b,3(;,) (=0,1,2,3)的定义为
显然,当==0时,四次广义Ball基函数退化为三次Ball基函数,QG-Ball曲线退化为传统三次Ball曲线。根据式(1)和(2),可以推出QG-Ball曲线具有与三次Ball曲线类似的优良几何性质,如凸包性、对称性、仿射不变性及变差缩减性等。
2 等弧长求解配置点
假设QG-Ball曲线的参数方程为(;,)= {(),()},则该曲线自身弧长的计算式为
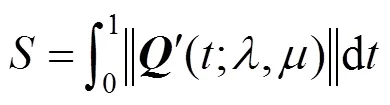
采用文献[24]中近似弧长参数化方法对QG-Ball曲线弧长进行均匀划分,计算出曲线上等弧长对应的一系列配置点(即等分点)及其配置点参数值。近似弧长参数化方法的基本步骤为:
步骤1. 根据式(3)计算QG-Ball曲线在区间[0,1]上的总弧长,选取弧长等分数,则每一小段曲线弧长为=/。
步骤2. 假设QG-Ball曲线弧长等份后的配置点为0=0,1,···,-1,=,其对应的配置点参数值为0=0,1,···,t-1,t=1。
步骤3. 构造如下-1个非线性方程
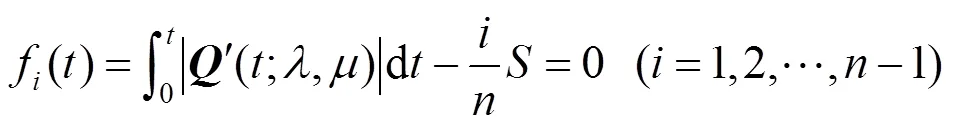
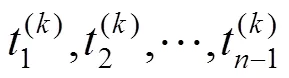
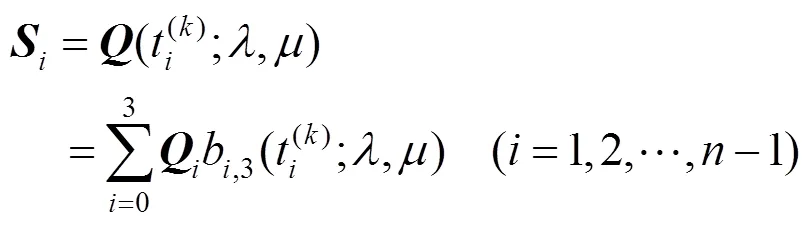
综上,运用上述弧长参数化方法,任意取定等分数,便可计算出QG-Ball曲线等弧长对应的配置点列和配置点参数值。
图1给出了QG-Ball曲线等弧长求解配置点的数值例子。并对带不同形状参数的QG-Ball曲线弧长进行了4等分,利用上述等弧长参数化方法简单高效地计算出其配置点列及配置点参数值,图中标记的黑点为离散出的配置点。表1给出了图1中所有曲线弧长4等分对应的配置点参数值。图2分别给出了QG-Ball曲线弧长5等份和8等份时求配置点和配置点参数值的例子。图中,曲线弧长5等分和8等份对应的配置点参数值分别见表2和3,QG-Ball曲线的形状参数取值为==0,1,2,3 (自下而上)。
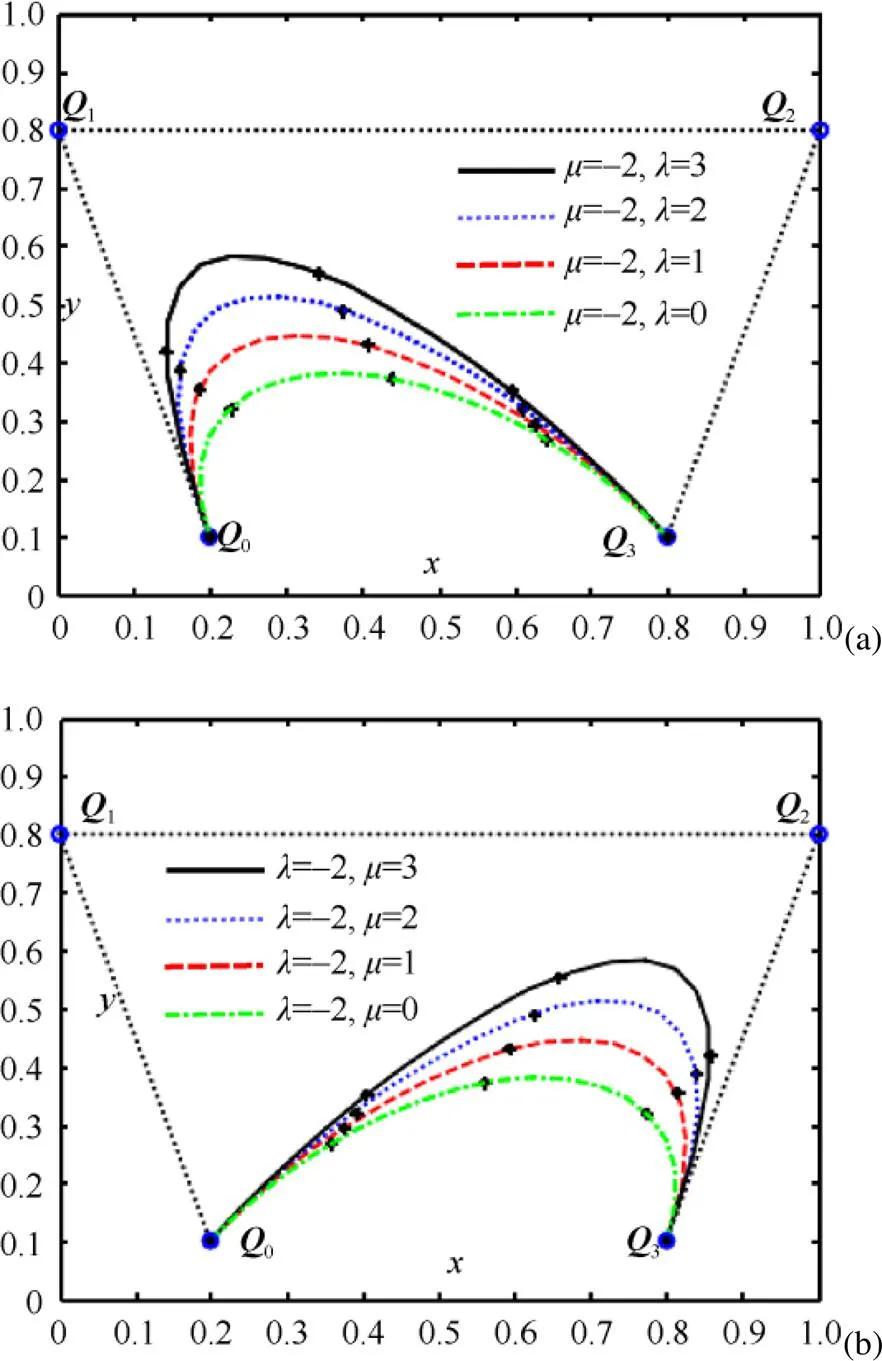
图1 QG-Ball曲线弧长4等分求解配置点
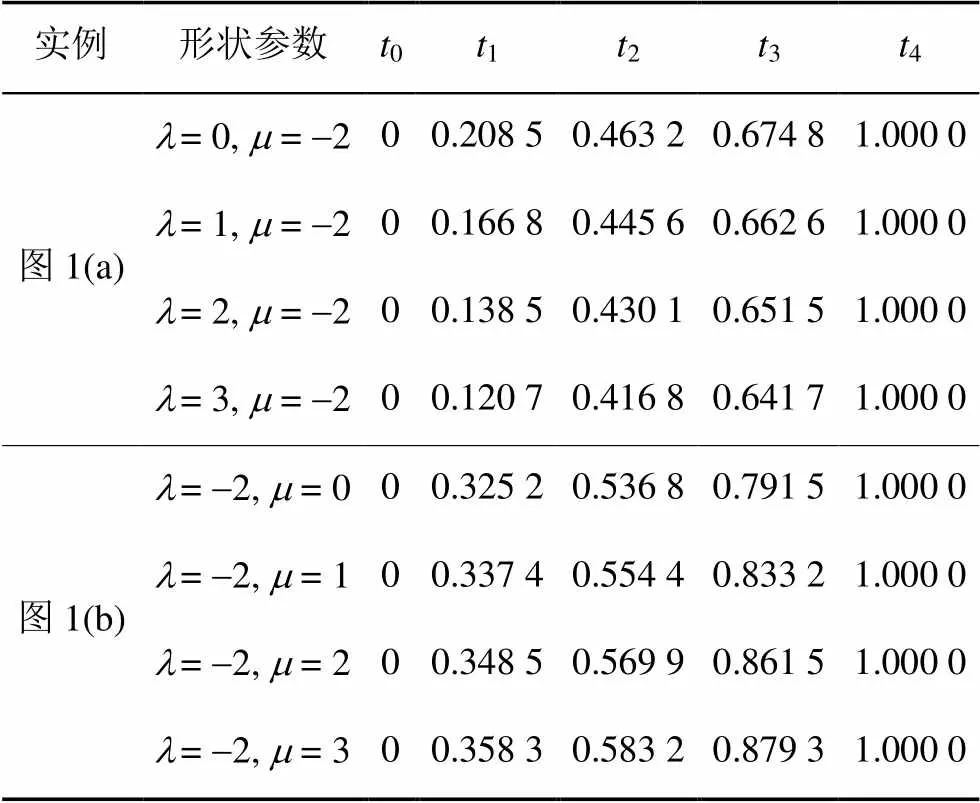
表1 图1中QG-Ball曲线弧长4等分时配置点参数取值
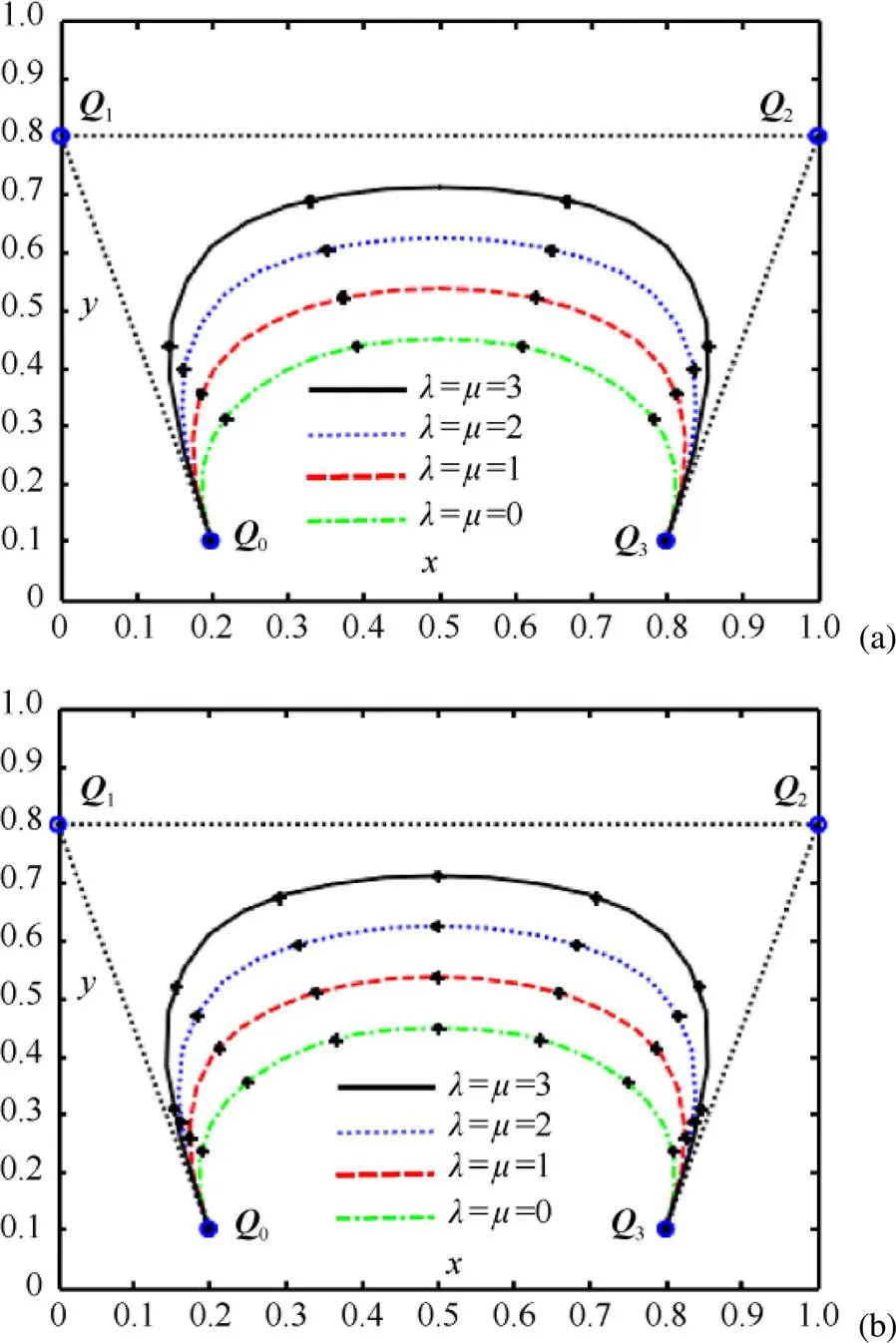
图2 QG-Ball曲线弧长5等分和8等分求解配置点
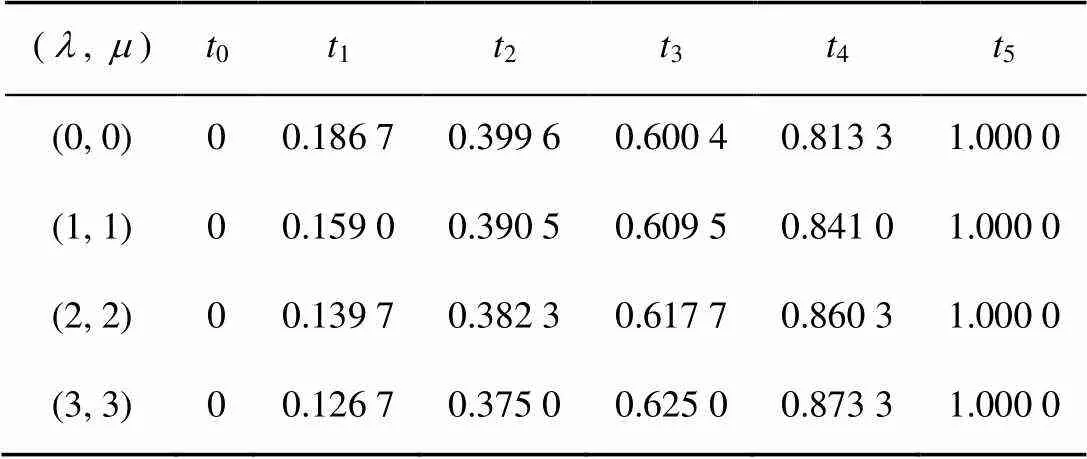
表2 图2(a)中QG-Ball曲线弧长5等分时配置点参数取值

表3 图2(b)中QG-Ball曲线弧长8等分时配置点参数取值
3 相邻QG-Ball曲线的近似合并
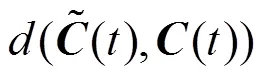
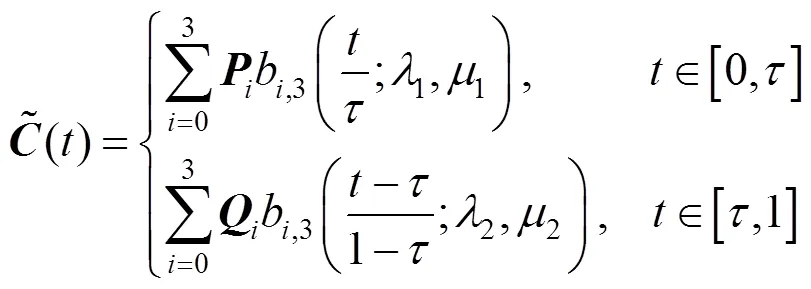
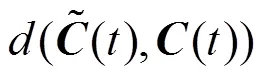
3.1 不保端点的近似合并
设以0,1,2,3,和0,1,2,3,为控制顶点的相邻QG-Ball曲线分别为(;1,1)和(;2,2),拟近似合并成另一条QG-Ball曲线,即
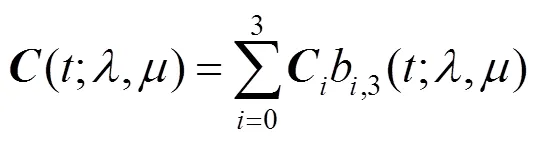
其中,=1+(1-t)2,=1+(1-t)2;(=0,1,2,3)为合并后曲线的控制顶点。本文求解合并曲线的算法步骤如下:
步骤1. 基于上述等弧长参数化方法,将曲线(;1,1)在区间[0,1]的弧长上进行1等分,并计算出相应的配置点参数值u(=0,1,···,1);类似地,计算出曲线(;2,2)当其曲线弧长2等分时对应的配置点参数值(=0,1,···,2),这里1与2均为大于或等于3的正整数。从而,得到待合并曲线(;1,1)上的1+1个点(u) (=0,1,···,1)和曲线(;2,2)上的2+1个点(v) (=0,1,···,2)。
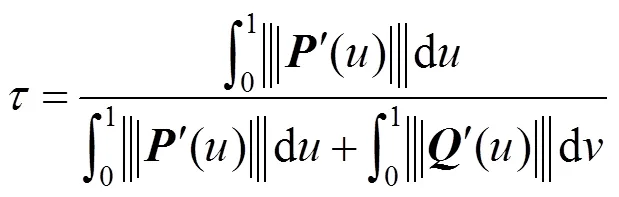
假设
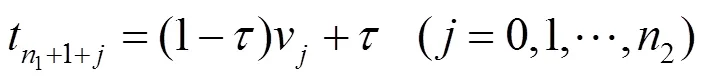
并令合并后的QG-Ball曲线(;,) (其控制顶点待求)满足
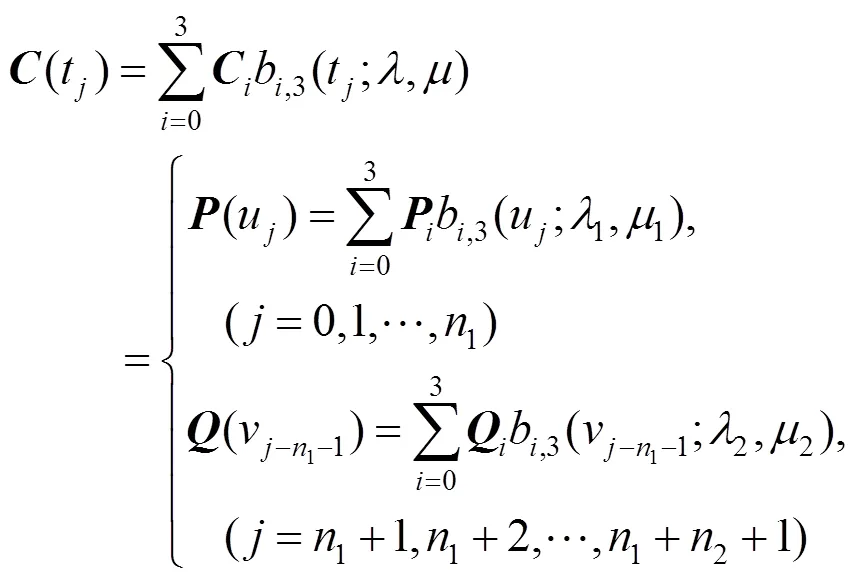
步骤3.将式(8)转化成矩阵乘积的形式,即
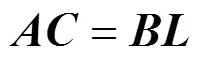
其中,=1+2+1。
因为b,3(;,)(=0,1,2,3)为一组线性无关的四次广义Ball基,同时参数t(=0,1,···,1+2+1)中至少有4个参数取值不同,所以矩阵是一个列满秩矩阵,且根据文献[25]中的广义逆矩阵理论(general inverse matrix theory,GIMT)可得向量超定方程组式(9)的最小二乘解为
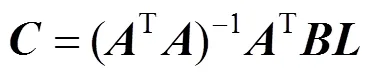
式(10)给出了计算合并曲线(;,)控制顶点的一个显式表达式。
步骤4.将上述步骤所得合并曲线的形状参数,和控制顶点(=0,1,2,3)代入曲线方程式(1)即可得合并曲线(;,)。
3.2 保端点的近似合并
基于3.1节方法,本节进一步研究QG-Ball曲线保端点插值的近似合并。在不保端点插值情形下,待合并曲线(;1,1)的左端点和曲线(;2,2)的右端点与合并曲线(;,)的两端点并没有重合。在曲线外形设计时,有时需要合并后QG-Ball曲线(;,)分别插值于曲线(;1,1)的左端点和曲线(;2,2)的右端点,该合并方式称为保端点插值的近似合并。为了满足曲线保端点插值近似合并的需求,结合QG-Ball曲线的端点性质
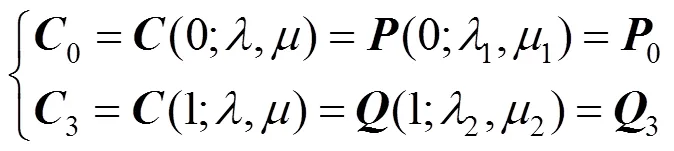
将式(11)代入式(8)中,可将式(8)重新写成矩阵乘积形式,即
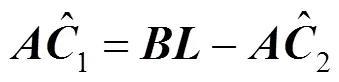
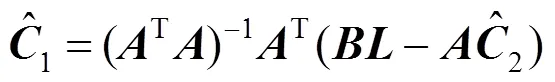
从而计算出保端点插值条件下合并曲线的控制顶点1和2,结合式(11)即可得到合并曲线(;,)的所有控制顶点。
4 实例与结果分析
4.1 数值实例
实例1.假设0(0,0),1(0.2,0.35),2(0.4,0.45)和3(0.6,0.38)为待合并曲线(;1,1)的控制顶点,而待合并曲线(;2,2)的控制顶点为0(0.6,0.38),1(0.8,0.3),2(0.85,0.25)和3(0.95,0)。本例中,待合并曲线(;1,1)和(;2,2)分别用红色与绿色实曲线表示,相应的控制多边形采用虚折线表示。合并后的曲线(;,)用黑色虚线表示,其控制多边形用黑色实线表示。
利用不保端点合并方法将2相邻曲线合并成另一条QG-Ball曲线(;,),这里细分参数由式(7)来确定。图3~4分别给出了当形状参数相同和不同时相邻曲线的合并实例。从图3~4中的近似合并结果来看,本文中的不保端点近似合并方法取得了很好的合并效果。表4给出了图3~4中合并曲线的控制顶点。
实例2.假设曲线(;1,1)的控制顶点为0(0,0.1),1(0.10,0.50),2(0.25,0.48),3(0.5,0.38),而另一条待合并曲线(;2,2)的控制顶点坐标为0(0.5,0.38),1(0.72,0.28),2(0.9,0.3),3(1,0.5)。图5~6分别给出了当形状参数相同和不同时相邻QG-Ball曲线的保端点插值合并实例。在图5~6中,待合并曲线(;1,1)和(;2,2)分别用红色与绿色实曲线表示,其控制多边形则分别采用与曲线颜色相同的虚折线表示;近似合并后的曲线(;,)用黑色虚线表示,其控制多边形为黑色实线。表5给出了图5~6中合并曲线(;,)的控制顶点。从图5~6的合并结果来看,本文保端点插值情形下的近似合并方法同样取得了不错的合并效果。
实例3.假设待合并曲线(;1,1)的控制顶点坐标为0(0.05,0.70),1(0.13,0.76),2(0.20,0.77)和3(0.32,0.73),而曲线(;2,2)的控制顶点坐标分别为0(0.32,0.73),1(0.56,0.65),2(0.62,0.15)和3(1.00,0.10)。图7给出了当形状参数相同时QG-Ball曲线保端点插值近似合并的实例,在图7中,2相邻待合并曲线在合并点处满足1光滑连续。图8则给出了当形状参数不同时QG-Ball曲线的保端点插值合并实例,图8中相邻待合并曲线在合并点处满足C1连续。
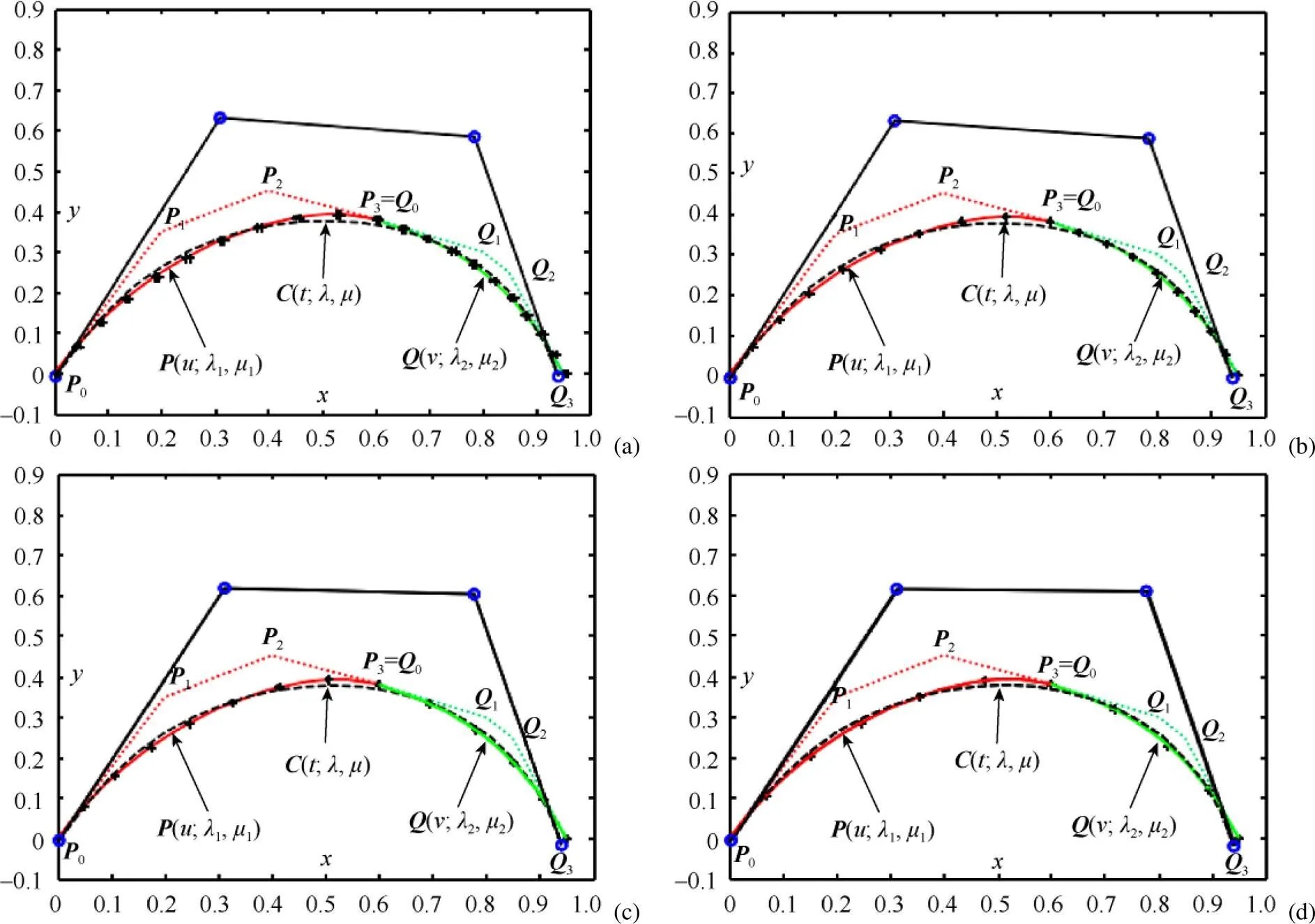
图3 带相同形状参数的QG-Ball曲线的不保端点近似合并,待合并曲线满足C0连续
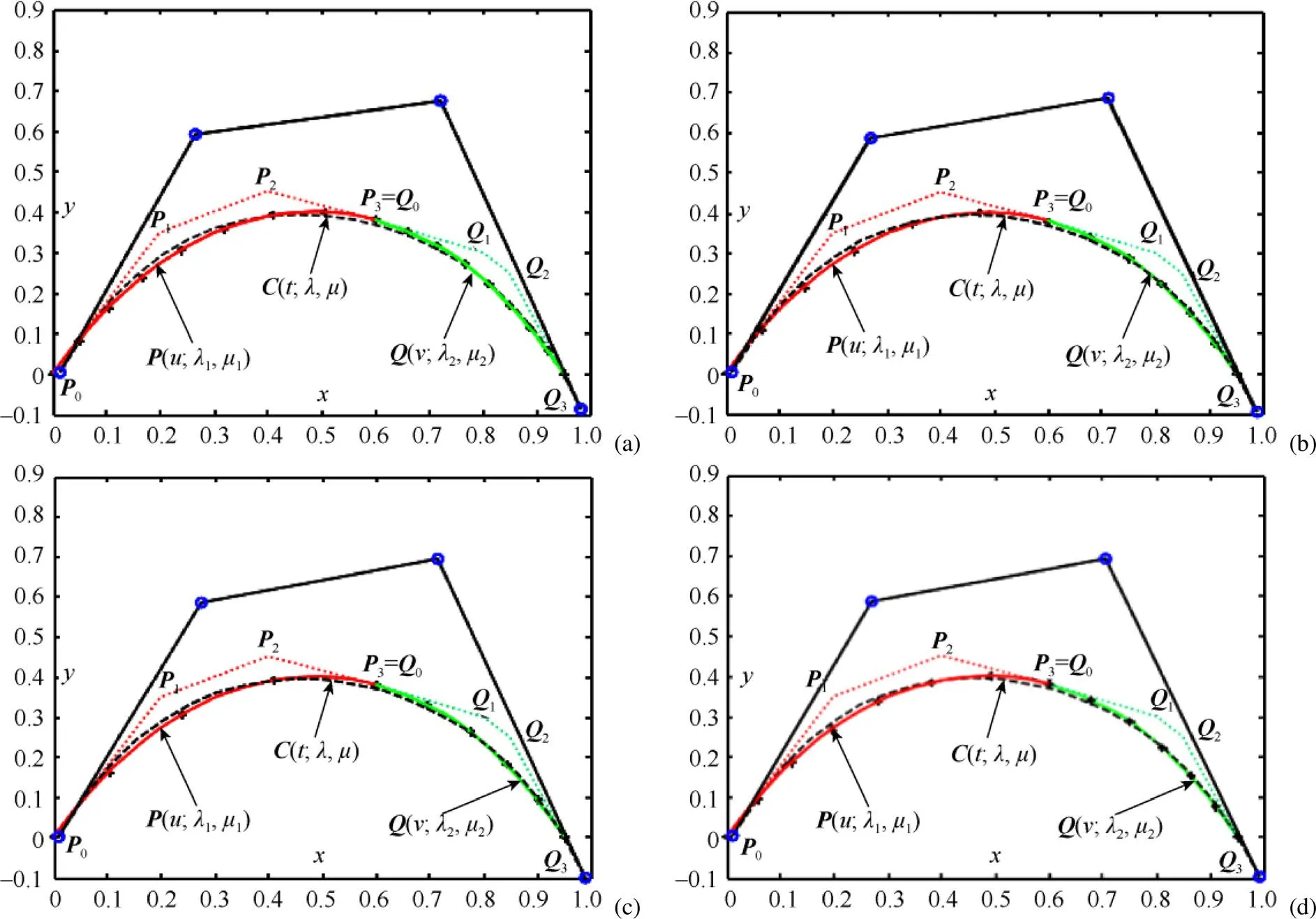
图4 带不同形状参数的QG-Ball曲线不保端点合并,待合并曲线满足C0连续
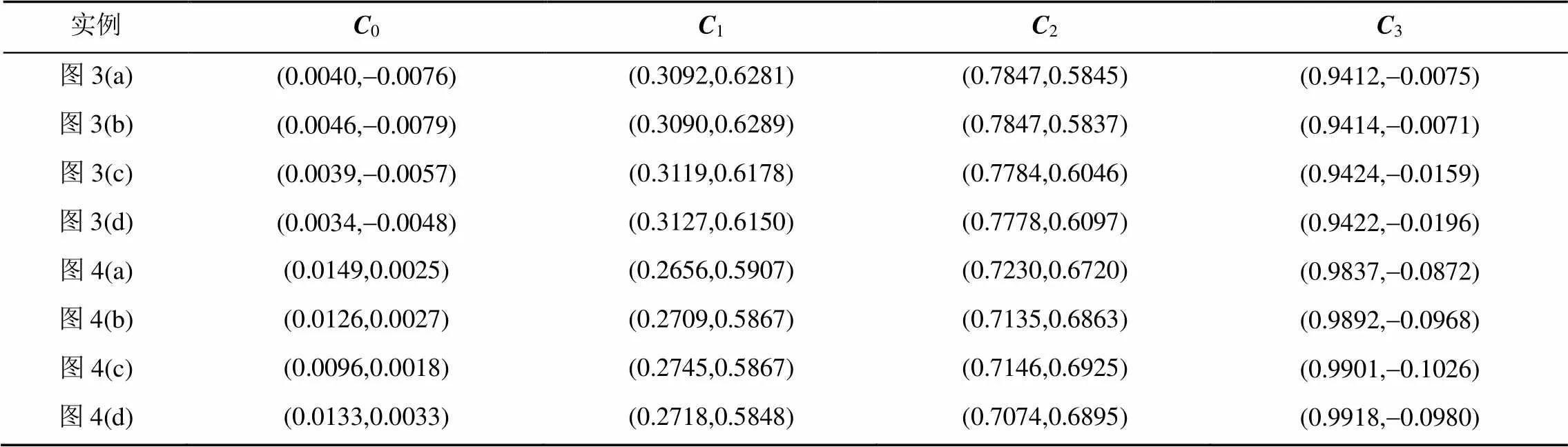
表4 图3~4中不保端点插值时合并曲线的控制顶点
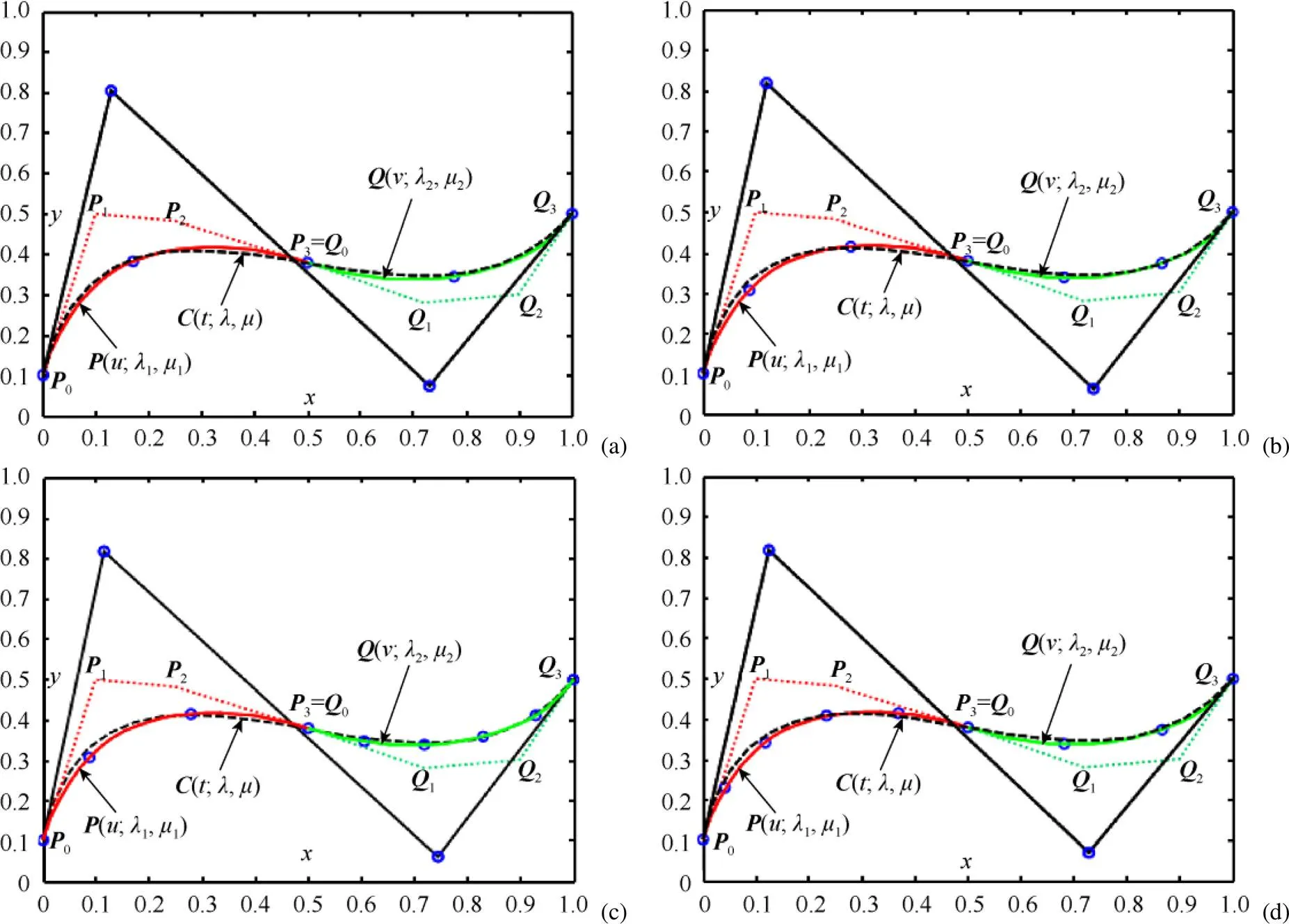
图5 带相同形状参数的QG-Ball曲线保端点插值的近似合并,待合并曲线满足C0连续
在图7~8中,待合并曲线(;1,1) (M型曲线)和(;2,2) (S型曲线)分别用红色与绿色实曲线表示,其控制多边形则分别采用与曲线颜色相同的虚折线表示;近似合并后的曲线(;,)用黑色虚线表示,其控制多边形为黑色实线。表6给出了图7~8中合并曲线(;,)的控制顶点。从图7~8中的合并效果来看,当合并曲线形状相差比较大时本文保端点插值情形下的近似合并方法也能取得不错的合并效果。
4.2 误差分析
为了验证文中所提出方法的近似合并效果,本文定义一种与文献[20]类似的近似合并误差公式。如前所述,式(7)中定义的细分参数为开区间(0,1)中的一个常数,分割点(;,)可将合并曲线(;,)分割为左右2段子曲线,且分别记为left(;,)和right(;,),则有
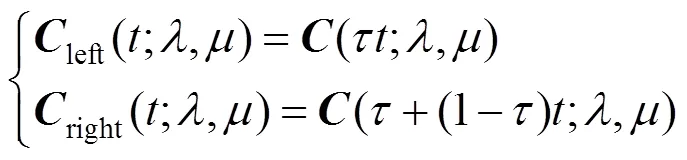
其中,Î[0,1]。通常,连续函数的2范数被用来测量不同参数曲线之间的距离[26],为此利用2范数定义如下的误差公式来度量或评价合并曲线(;,)与待合并曲线(;1,1)和(;2,2)之间的合并效果,即
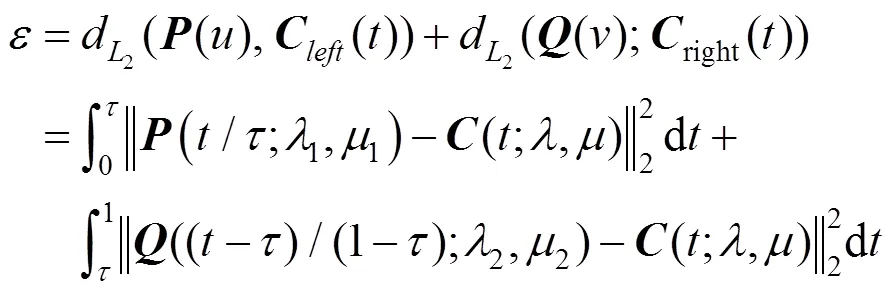
显然,通过积分换元可将误差公式转化为
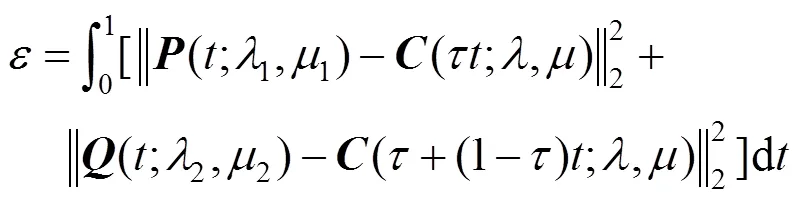
其中,运算符为向量函数的L2范数。式(15)和(16)的几何意义为:合并曲线与2相邻待合并曲线之间的“距离”(注:该距离是由向量函数的L2范数来度量的)被用来定义其之间的合并误差。显然,式(15)和(16)中的合并误差公式可以较好地评价本文方法近似合并的效果。
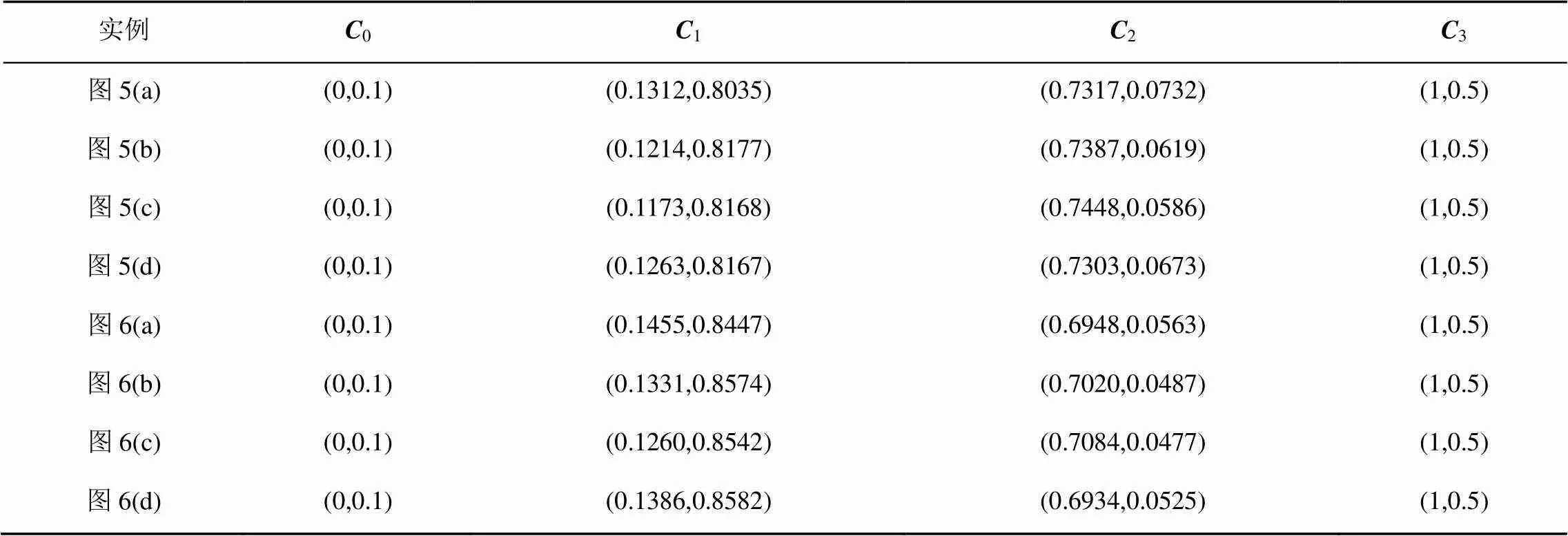
表5 图5~6中保端点插值时合并曲线的控制顶点
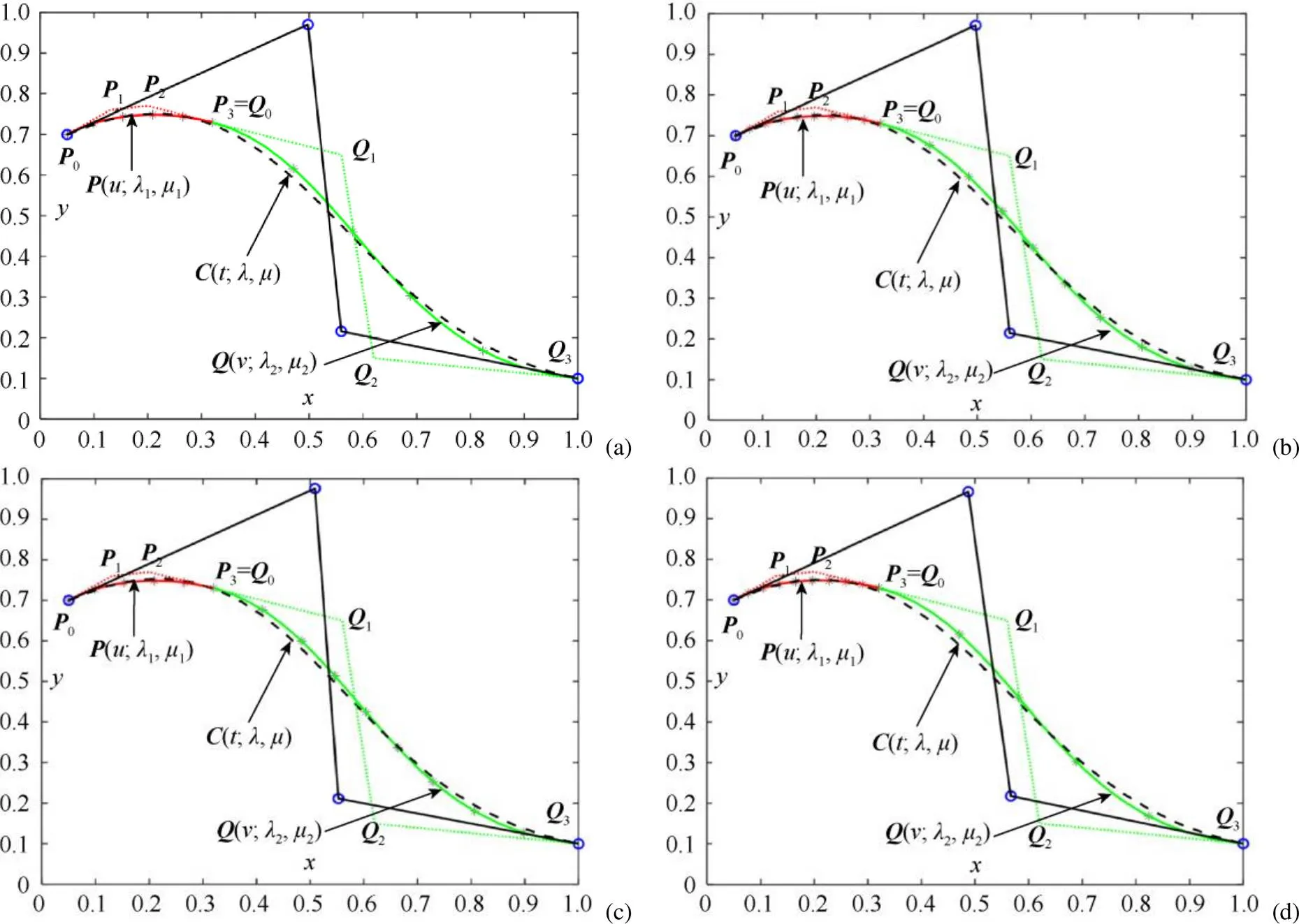
图7 带相同形状参数的QG-Ball曲线保端点插值的近似合并,待合并曲线满足G1连续
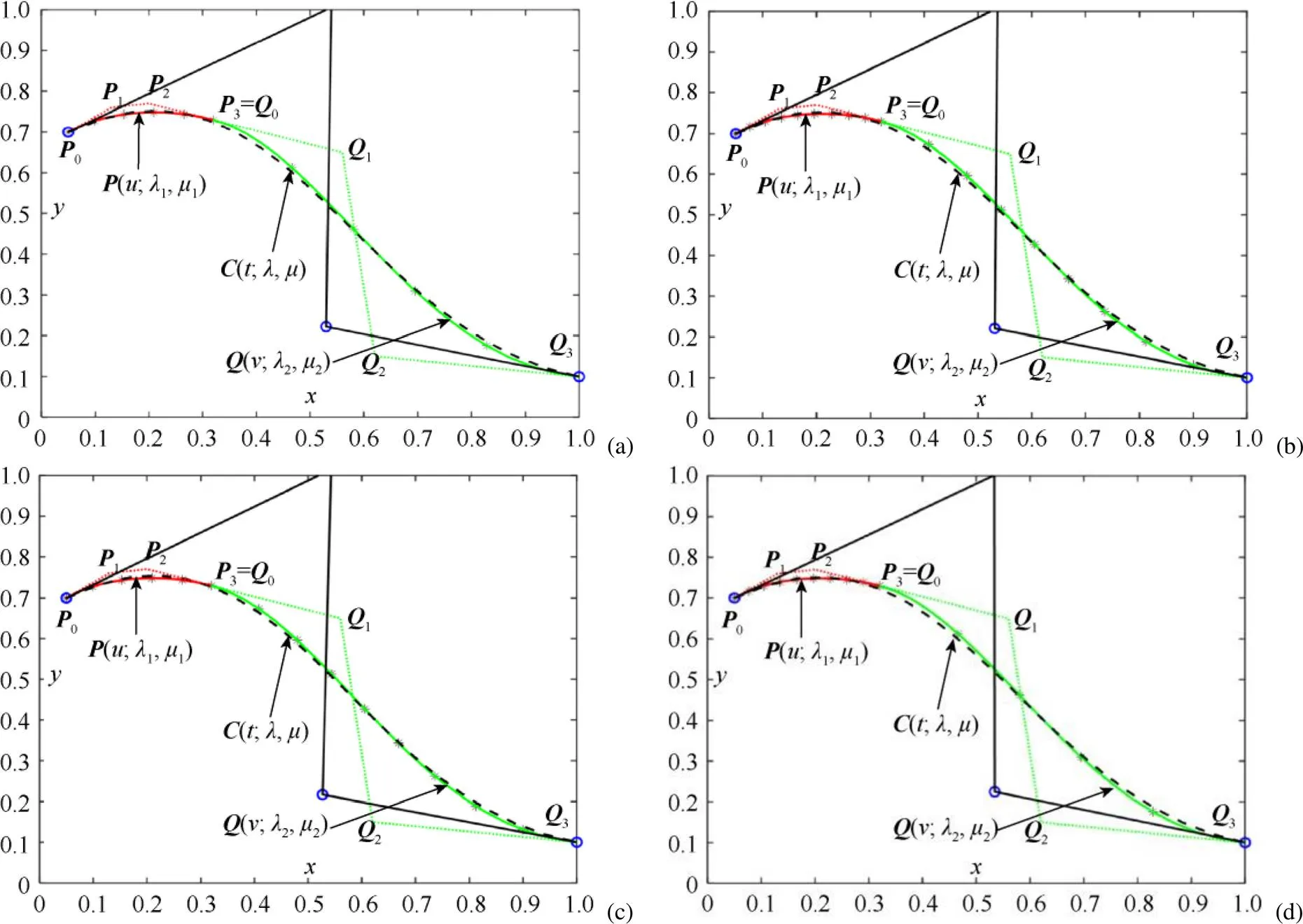
图8 带不同形状参数的QG-Ball曲线保端点插值的近似合并,待合并曲线满足C1连续
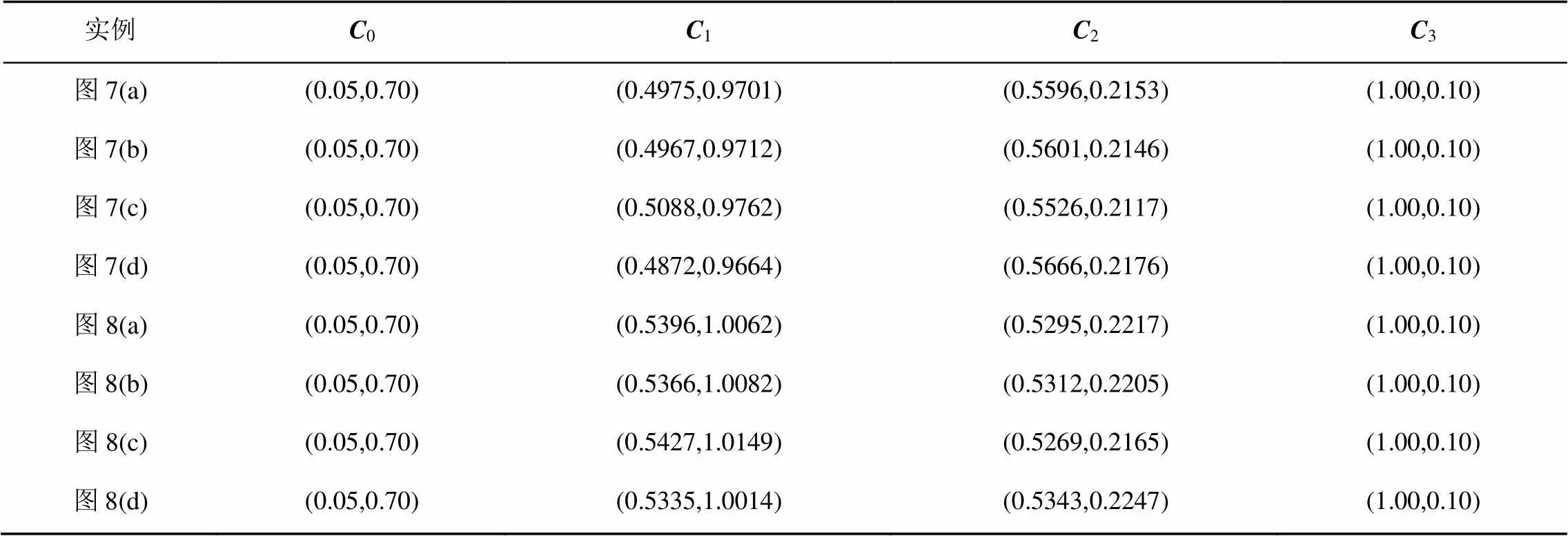
表6 图7~8中保端点插值时合并曲线的控制顶点
表7给出了图3~8中数值实例的近似合并误差。显然,本文方法在不保端点和保端点插值的情形下均可获得较小的近似合并误差,结果和主观视觉评价是一致的。数值实验结果表明本文方法可以有效地实现QG-Ball曲线的合并逼近。
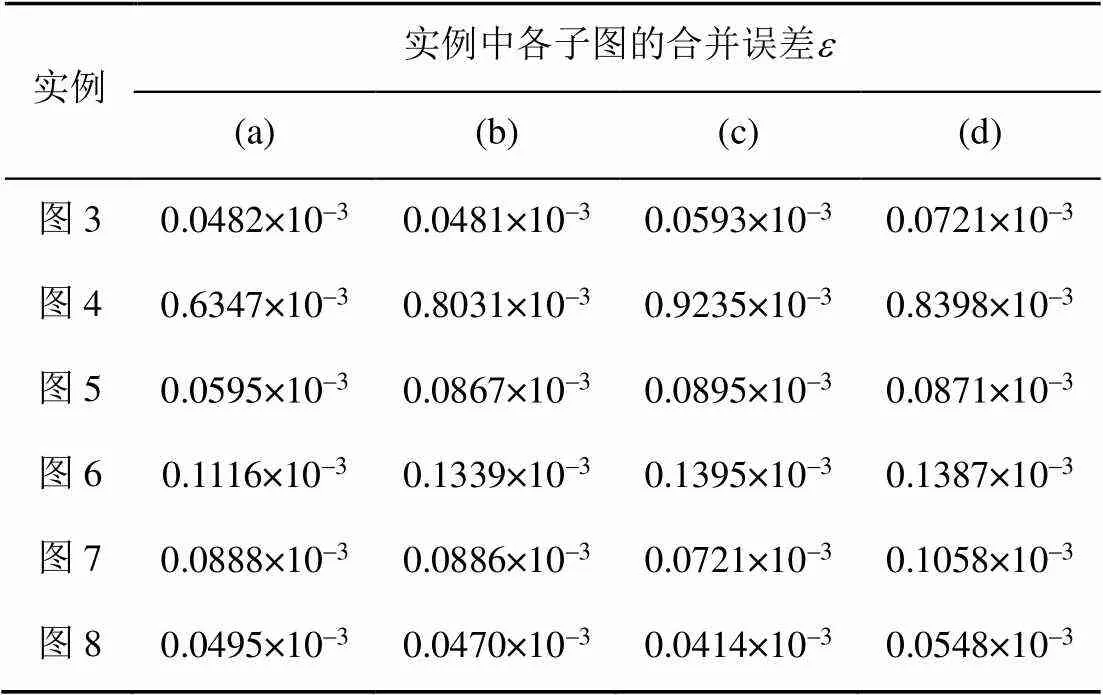
表7 图3~8中实例的近似合并误差
5 结 论
基于QG-Ball曲线基本理论,针对该曲线难以合并的问题,提出了一种基于广义逆矩阵理论和弧长参数化的QG-Ball曲线近似合并方法。本文方法不仅可以直接得到计算合并曲线控制顶点的一个显式表达式,还给出了合并误差的具体计算公式。数值算例结果表明,本文方法可以高效地实现QG-Ball曲线的近似合并,不仅易于操作且误差计算简单,并方便推广到其他类型曲线的合并,如文献[27-28]中的高次带参SG-Bézier曲线的近似合并。另外,如何选择最优细分参数以及实现QG-Ball曲面的近似合并等,是值得今后进一步研究的课题。
[1] BALL A A. CONSURF. Part two: description of the algorithms[J]. Computer-Aided Design, 1975, 7(4): 237-242.
[2] HU S M, WANG G Z, JIN T G. Properties of two types of generalized ball curves[J]. Computer-Aided Design, 1996, 28(2): 125-133.
[3] 丁友东, 李敏, 华宣积. 广义Ball曲线的性质及其应用[J]. 应用数学学报, 2000, 23(4): 580-595.
DING Y D, LI M, HUA X J. Generalized Ball curves' properties and its application[J]. Acta Mathematicae Applicatae Sinica, 2000, 23(4): 580-595 (in Chinese).
[4] 邬弘毅. 两类新的广义Ball曲线[J]. 应用数学学报, 2000, 23(2): 196-205.
WU H Y. Two new types of generalized Ball curves[J]. Acta Mathematicae Applicatae Sinica, 2000, 23(2): 196-205 (in Chinese).
[5] 沈莞蔷, 汪国昭. Ball基的推广[J]. 软件学报, 2005, 16(11): 1992-1999.
SHEN W Q, WANG G Z. Extension of the Ball basis[J]. Journal of Software, 2005, 16(11): 1992-1999 (in Chinese).
[6] 蒋素荣, 王国瑾. Bézier曲线到Wang-Ball曲线的转换矩阵及其应用[J]. 计算机学报, 2005, 28(1): 75-80.
JIANG S R, WANG G J. Conversion matrix from Bézier curve to Wang-Ball curve and its application[J]. Chinese Journal of Computers, 2005, 28(1): 75-80 (in Chinese).
[7] 余宏杰. Wang-Said型广义Ball曲线的细分算法[J]. 计算机辅助设计与图形学学报, 2009, 21(5): 600-605.
YU H J. Subdivision algorithm for Wang-Said type generalized Ball curves[J]. Journal of Computer-Aided Design & Computer Graphics, 2009, 21(5): 600-605 (in Chinese).
[8] LIU G, WANG G J. Explicit multi-degree reduction of Said-Bézier generalized Ball curves[J]. Journal of Software, 2010, 21(6): 1473-1479.
[9] 吴晓勤, 韩旭里. 四次带参Ball曲线的形状分析[J]. 应用数学学报, 2011, 34(4): 671-682.
WU X Q, HAN X L. Shape analysis of quartic Ball curve with shape parameter[J]. Acta Mathematicae Applicatae Sinica, 2011, 34(4): 671-682 (in Chinese).
[10] 王成伟. 三次Ball曲线的扩展[J]. 工程图学学报, 2008, 29(1): 77-81.
WANG C W. Extension of cubic Ball curve[J]. Journal of Engineering Graphics, 2008, 29(1): 77-81 (in Chinese).
[11] 熊建, 郭清伟. 广义Said-Ball 曲线[J]. 数值计算与计算机应用, 2012, 33(1): 32-40.
XIONG J, GUO Q W. Generalized Said-Ball curves[J]. Journal on Numerical Methods and Computer Applications, 2012, 33(1): 32-40 (in Chinese).
[12] SAA K. Extension quintic Wang-ball curves and surfaces[J]. Far East Journal of Mathematical Sciences, 2013, 75: 185-201.
[13] HU G, LUO L, LI R, et al. Quartic generalized Ball surfaces with shape parameters and its continuity conditions[C]//2017 IEEE Conference on Computer Science & Network Technology. New York: IEEE Press, 2017: 5-10.
[14] 李军成, 李兵, 易叶青. 带参数的同次Ball曲线[J]. 中国图象图形学报, 2018, 23(6): 896-905.
LI J C, LI B, YI Y Q. Ball curve of the same degree with a parameter[J]. Journal of Image and Graphics, 2018, 23(6): 896-905 (in Chinese).
[15] 刘华勇, 李璐, 张大明. 带形状参数的四次Ball曲线[J]. 山东大学学报: 工学版, 2011, 41(2): 23-28.
LIU H Y, LI L, ZHANG D M. Quadratic Ball curve with multiple shape parameters[J]. Journal of Shandong University: Engineering Science, 2011, 41(2): 23-28 (in Chinese).
[16] QIN X Q, LV D, HU G, et al. Subdivision algorithm of quartic Q-Ball curves with shape parameters[C]//2018 IEEE 3rd International Conference on Image, Vision and Computing (ICIVC). New York: IEEE Press, 2018: 711-715.
[17] HU G, LV D, QIN X Q. Subdivision algorithm of quartic Q-Ball surfaces with shape parameters[M]//Advances in Intelligent Systems and Computing. Cham: Springer International Publishing, 2018: 144-151.
[18] HU S M, TONG R F, JU T, et al. Approximate merging of a pair of Bézier curves[J]. Computer-Aided Design, 2001, 33(2): 125-136.
[19] TAI C L, HU S M, HUANG Q X. Approximate merging of B-spline curves via knot adjustment and constrained optimization[J]. Computer-Aided Design, 2003, 35(10): 893-899.
[20] 郭清伟. 两相邻Bézier曲线的近似合并[J]. 计算机辅助设计与图形学学报, 2005, 17(10): 2275-2280.
GUO Q W. Approximate merging of a pair of Bézier curves[J]. Journal of Computer Aided Design & Computer Graphics, 2005, 17(10): 2275-2280 (in Chinese).
[21] CHENG M, WANG G J. Approximate merging of multiple Bézier segments[J]. Progress in Natural Science, 2008, 18(6): 757-762.
[22] PUNGOTRA H, KNOPF G K, CANAS R. Merging multiple B-spline surface patches in a virtual reality environment[J]. Computer-Aided Design, 2010, 42(10): 847-859.
[23] LU L Z. An explicit method for G3merging of two Bézier curves[J]. Journal of Computational and Applied Mathematics, 2014, 260: 421-433.
[24] 方逵, 谭元发, 吴泉源. 近似弧长参数化的一种数值算法[J]. 工程数学学报, 2002, 19(3): 123-127.
FANG K, TAN Y F, WU Q Y. An numerical algorithm of nearly arc-length parameterization[J]. Chinese Journal of Engineering Mathematics, 2002, 19(3): 123-127 (in Chinese).
[25] 陈国栋, 王国瑾. 基于广义逆矩阵的Bézier曲线降阶逼近[J]. 软件学报, 2001, 12(3): 435-439.
CHEN G D, WANG G J. Degree reduction approximation of Bézier curves by generalized inverse matrices[J]. Journal of Software, 2001, 12(3): 435-439 (in Chinese).
[26] RABABAH A, MANN S. Iterative process for G2-multi degree reduction of Bézier curves[J]. Applied Mathematics and Computation, 2011, 217(20): 8126-8133.
[27] HU G, WU J L, QIN X Q. A novel extension of the Bézier model and its applications to surface modeling[J]. Advances in Engineering Software, 2018, 125: 27-54.
[28] HU G, BO C C, WEI G, et al. Shape-adjustable generalized Bézier surfaces: construction and its geometric continuity conditions[J]. Applied Mathematics and Computation, 2020, 378: 1-28.
Approximate merging of QG-Ball curves using GIMT and arc-length parameterization
HU Xian-zhi1, LIANG Yan2,3, LYU Dan4, HU Gang4
(1. Division of Informationize Management, Xi’an University of Technology, Xi’an Shaanxi 710048, China; 2. School of Electronics and Information Engineering, Xi’an Jiaotong University, Xi’an Shaanxi 710049, China; 3. School of Technology, Xi’an Siyuan University, Xi’an Shaanxi 710038, China; 4. School of Science, Xi’an University of Technology, Xi’an Shaanxi 710054, China)
As an effective technique for the design of complex curve, approximate merging has generated much attention from scholars and been in wide use in CAD/CAM. To address the difficulty in merging generalized Ball curves with parameters, this paper proposed a new method for the approximate merging of QG-Ball curves based on generalized inverse matrix theory (GIMT) and arc-length parameterization. Given two QG-Ball curves, we first calculate a sequence of equal arc-length parameters of the QG-Ball curves by using approximate arc-length parameterization algorithm; Based on the sequence of parameters GIMT, and curve fitting algorithm, an explicit expression was presented to calculate the control points of approximate merged QG-Ball curve. To verify the effectiveness of the method, numerical examples were provided and the merging errors were discussed. The experimental results show that the proposed method not only can efficiently realize the approximate merging of QG-Ball curves, which is of high operability and easy for error calculation, but also can be extended to other curves conveniently.
quartic generalized Ball curves; shape parameter; approximate merging; general inverse matrix; arc-length parameterization
TP 391.4
10.11996/JG.j.2095-302X.2021050790
A
2095-302X(2021)05-0790-11
2021-02-23;
2021-04-02
23 February,2021;
2 April,2021
国家自然科学基金项目(51875454);陕西省教育厅专项科学研究计划项目(19JK0686)
National Natural Science Foundation of China (51875454); Special Scientific Research Project of Shaanxi Provincial Department of Education (19JK0686)
胡先智(1978–),男,湖北麻城人,工程师,硕士。主要研究方向为数据挖掘、图形图像处理。E-mail:huxianzhi@xaut.edu.cn
HU Xian-zhi (1978-), male, engineer, master. His main research interests cover data mining and graphics. E-mail:huxianzhi@xaut.edu.cn

