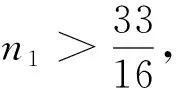基于度参数的[a,b]-因子存在的一个充分条件
冯宝成,高洪秀,岳 军,李宏升
(青岛理工大学 理学院,青岛 266525)
1 简单图与因子理论
本文考虑的图G为无向简单图[1],设G=(V(G),E(G)),其中V(G)是顶点集,E(G)是边集。对于x∈V(G),x在G中的度用dG(x)表示。G-S表示去掉S中的点以及和S相关联的边得到的图。若F是G的一个支撑子图且对任意x满足g(x)≤dF(x)≤f(x),其中g(x),f(x)是定义在顶点集上的两个整数值函数,则F是G的(g,f)-因子,当g(x)=a,f(x)=b时称F为[a,b]-因子,若a=b=k,则称F是图G的一个k-因子[2]。
对于图的研究有许多分支,而因子理论是其中最重要、最热门的分支之一。图因子的研究始于丹麦数学家PETERSE,19世纪初他证明了2连通三次图的1-因子存在性,TUTTLE推广1-因子定理得出f-因子存在的充要条件,LOVASZ[3]对顶点度约束条件的研究得到(g,f)-因子,KATERINIS[4]给出图因子存在的度条件,随后关于图因子的研究结果大量涌现,如[a,b]-因子,k-因子,1-因子等等。郝国辉研究了完全三部图的因子存在性[5]。王璐把无爪图和2-因子理论相结合[6],得出无爪图存在2-因子的一个条件。在受限图[7]中可以进一步研讨因子的存在性条件。
2 主要结果及其证明
2.1 本文结果
图参数在因子理论研究中有重要意义,尤其顶点度、阶数与图因子的关系极其密切,文献[8]通过对顶点度和阶数的分析得出图因子的一个存在条件,本文进一步分析了不相邻顶点的度和与图因子的关系,得到[a,b]-因子存在的又一个充分条件。

2.2 定理证明
证明结论需要两个已证的引理。
引理1[3]设0 其中,s=|S|;t=|T|。 引理2[4]设0 dG-S(x)≤a-1 证明 当a=b=k≥2时,则结论成立[2]。以下假设a 假设G无[a,b]-因子, 由引理1知, 存在V(G)的两个不相交子集S,T使θ(S,T)<0成立, (1) 且T是使θ(S,T)<0的极小子集。由引理2知, dG-S(x)≤a-1,∀x∈T (2) 情况1T=φ 由引理1知,S≠φ,又T=φ,故t=0,dG-S(T)=0, bs-at+dG-S(T)=bs>0 与式(1)矛盾。 情况2T≠φ 设h1=min{dG-S(x)∶x∈T},且令x1∈T使dG-S(x1)=h1。 子情况2.1NT[x1]≠T 再设h2=min{dG-S(x)∶x∈T-NT[x1]},且令x2∈T-NT[x1]使dG-S(x2)=h2。 (3) 再令p=|NT[x1],t≥p+1,p≤h1+1。由式(1)和式(3)得 -1≥bs-at+dG-S(T)≥ bs-at+h1p+h2(t-p)≥ (h1-h2)(h1+1)+h2(p+1)+bs-a(n-s)≥ 则 (4) 故式(4)成立。 子情况2.2NT[x1]=T 由式(1)得 -1≥bs-at+dG-S(T)≥bs-at+h1t (5) 由顶点度条件b≤δ(G)≤dG(x1)≤h1+s,所以s≥b-h1。将s≥b-h1代入式(5)得 b(b-h1)+(h1-a)t+1≤0 (6) 因为NT[x1]=T,故t (7) 定理证毕。 现代因子理论研究主要包括因子的存在性条件、特定性质的因子、因子的临界性以及因子分解4个方面,而因子存在性的充分条件与图的阶数和顶点度有很大关系。本文结论和文献[8]都是从这两个方面探讨因子的存在条件,二者关于顶点度条件是一致的,而本文对图阶数的要求有所改进,本文结论中图的阶数条件为 文献[8]中图的阶数要求满足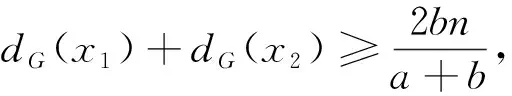

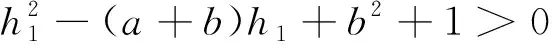
3 结论