半马尔可夫跳变系统在分数布朗运动干扰下的采样控制
孟 静,解 静
(青岛理工大学 信息与控制工程学院,青岛 266525)
半马尔可夫过程是能够更接近于真实工程情况的模拟过程,它有着极大的实际研究潜力和深厚的理论支持,其研究所得的成绩直接关系到生产实际中的关键环节,已经得到了国际上广大学者的重视,并且部分研究成果已经被成功地应用于网络控制、容错控制和现代通信技术等领域。采样控制是指在采样周期内,系统将采样瞬间的信息保持恒定。采样控制器具有安装方便、效率高、可靠性好等优点。WANG Jing等讨论了具有半马尔可夫跳跃拓扑的复杂动态网络的广义耗散同步问题,其中不同拓扑之间的切换是由半马尔可夫跳跃拓扑触发的马尔可夫过程,核心是利用一种新的采样数据控制器,使同步误差系统随机稳定[1]。WU Tianyu等研究了半时滞系统的H∞指数同步问题,利用采样控制方法,实现了马尔可夫跳变复杂动态网络的控制;通过构造一个具有环泛函的合适李雅普诺夫泛函,并采用先进的不等式方法,给出了时滞半马尔可夫跳跃复杂动态网络H∞指数同步的充分条件[2]。WANG Jing等研究了半马尔可夫跳变惯性神经网络的有限时间同步问题,利用采样数据控制来减轻有限通信带宽的负担[3]。LIU Yuan等研究了具有复杂动态网络同步问题的半马尔可夫过程,半马尔可夫过程是用于描述不同模态之间切换的网络拓扑;同时,在采样系统中考虑了一个恒定的信号传输延迟数据控制器处理同步问题,采用内存采样数据控制方案来保证主从系统的同步[4]。王庆等通过把采样区间划分为4个区间,研究了马尔可夫跳变系统的采样控制问题。针对这个系统,在采样区间内建立2个状态空间表达式,利用其建立了一种新颖的分段泛函[5]。田佳萍等研究了马尔可夫模型的神经网络采样控制的主从同步问题,在零输入策略的框架下提出了一种新型的采样控制器[6]。综上,研究基于马尔可夫系统的采样控制方法,如何设计采样控制器是需要解决的第一个关键技术。
分数布朗运动具有平稳增量、自相似性和长程相关性等性质,这是许多自然现象和社会现象的内在特性,所以分数布朗运动构成的模型是使用最广泛的模型之一。D’AURIA Bernardo等研究了一个反射马尔可夫调制布朗运动,该运动的漂移扩散系数和2个边界由有限状态空间不可约连续时间马尔可夫链共同调制[7]。HE Miao等研究了一类带有分数布朗运动,具有马尔可夫跳变参数的随机非线性系统的事件触发自适应动态面全状态控制问题[8]。DONG Hailing等研究了部分未知过渡率、随机噪声和随机耦合强度下的带有分数布朗运动马尔可夫交换复杂网络的同步问题[9]。目前关于带分数布朗运动的马尔可夫系统的稳定性分析,大都采用指数型李雅普诺夫函数,且对此进行研究的文献较少,本文选取了与Malliavin导数有关的新型Lyapunov泛函,利用线性矩阵不等式得到了Malliavin导数部分使得系统有限时间随机有界的条件, 这是本文需要解决的第二个关键技术。
综上,本文将对分数布朗运动干扰下半马尔可夫跳变系统的采样控制问题进行研究,为解决上述两个关键技术问题,本文将研究采样控制器的设计、系统有限时间随机有界性分析,最后要通过数值算例来验证所提方法和技术的有效性。
1 问题描述与假设
定义连续时间离散状态的齐次半马尔可夫过程为r(t):r(t)∈S={1,2,…,s},其中连续时间t≥0,模态转移速率定义为
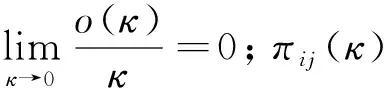
在完备概率空间上,考虑一类受分数布朗运动干扰的半马尔可夫跳变系统:
(1)
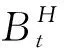
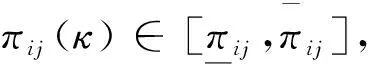
定义1[10](有限时间随机有界)对半马尔可夫跳变系统(1),如果存在常数c1,c2(c1
E{xΤ(0)P(r(0))x(0)}≤c1⟹E{xΤ(t)Pix(t)}≤c2,∀t∈[t1,t2]
则称系统(1)在u(t)=0下是关于(c1,c2,T,Pi)有限时间随机有界的。
式中:E{·}为数学期望;xT(t)为系统状态向量x(t)的转置,这里的T为转置。
引理1[11]对任意矩阵W>0, 标量γ1和γ2满足γ2>γ1,设矢量函数为w:[γ1,γ2]→Rn,则下列积分不等式成立:
2 主要结果
2.1 采样控制器设计
定义一个序列tk(k=0,1,…,s)为采样时间,且满足t0 0≤tk+1-tk=a,a>0,∀k≥0 (2) 在采样时间tk(k=0,1,…,s)的定义下,系统(1)的控制信号由零阶保持器生成,由此定义的采样反馈控制器为 u(t)=Kix(tk),t∈[tk,tk+1],i∈S, (3) 式中:Ki为需要设计的反馈增益矩阵;[tk,tk+1]之间控制器的数据通过零阶保持器保持不变;x(tk)为采样瞬间tk时状态x(t)的测量值。 令τ(t)=t-tk,t∈[tk,tk+1],则式(3)等价于: u(t)=Kix(t-τ(t)),t∈[tk,tk+1] (4) 对t∈[tk,tk+1],将式(4)代入式(1)得到闭环系统(5): (5) 下面讨论闭环系统(5)的有限时间随机有界性问题。 定理1对于任意的i=1,2,…,q,在有限时间区间[0,T]上,如果存在矩阵Si,Ki和对称正定矩阵Xi,R1,R2使得以下线性矩阵不等式成立: (6) (7) 那么具有采样反馈控制器(3)的系统(1)是有限时间随机有界的。矩阵中*为对称矩阵中对称项的省略号。 证明:根据文献[12],在有限时间区间[0,T]上对i∈S构造如下新型Lyapunov泛函: (8) 那么在Malliavin导数定义下对V(x(t),i,t)求无穷小算子LH可得 (9) (10) 在时间区间[0,T]中,有以下不等式成立: (11) 将式(10),式(11)代入式(9)可得 (12) 下面分别证明E{I1}<0和E{t2H-1I2}<0。首先讨论关于E{I1}<0的证明,显然,下列不等式成立: (13) (14) (15) 其中 然后讨论关于E{t2H-1I2}<0的证明。现定义时间变量γ(t)(0<γ(t) 那么根据引理1可得 (16) (17) 由式(17)可推导得 (18) 将式(18)代入式(16)得 (19) (20) 综上,可得E{LHV(x(t),i,t)}=E{I1}+E{t2H-1I2}<0。再根据定义1和文献[12]的结论可知,闭环系统(5)是有限时间随机有界。证明完毕。 考虑具有3个半马尔可夫跳变模式的系统(1),即i=1,2,3,定义其矩阵参数为 半马尔可夫过程的概率速率矩阵为 驻留时间κ=0.886 25, 概率密度函数gi(κ)服从Weibull分布,具体参数取值分别为g1(κ)=2κe-κ2,g2(κ)=3κ2e-κ3,和g3(κ)=5κ4e-κ5。定义T=15和H=0.7。利用MATLAB可求得满足定理1条件的下列矩阵的可行解: 因此,该数值算例在定理1条件下是有限时间随机有界的。 在分数布朗运动干扰下,本文对半马尔可夫跳变系统的有限时间随机有界性问题进行了分析。首先给出了采样控制器的设计;然后,通过建立与Hurst指数相关且带有二重积分的新型Lyapunov泛函,得到了闭环系统有限时间随机有界的充分条件;最后数值算例验证了本文所提方法的可行性。本文研究的分数布朗运动和采样控制器设计方法将为后续研究复杂动态网络提供参考价值。2.2 有限时间随机有界性分析
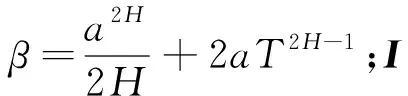
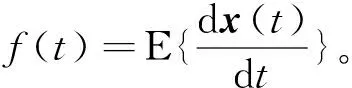
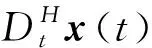
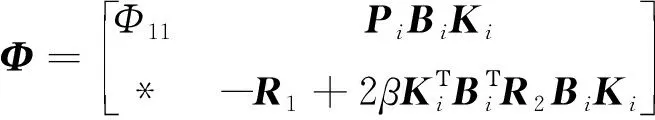
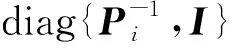
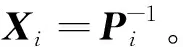
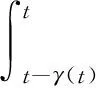
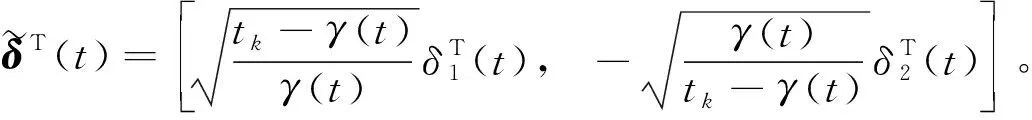


3 数值算例

4 结束语

