淹没深度对离心式叶轮模态参数的影响

曾永顺 ， 刘妍琦， 邓柳泓， 刘岚林， 姚志峰,2， 肖若富,2

(1.中国农业大学 水利与土木工程学院，北京 100083； 2.北京市供水管网系统安全与节能工程技术研究中心，北京 100083)

在动静干涉[1]、旋转失速[2]以及空化流动[3]等影响下，叶轮存在承受高幅值应力的风险. 在水体附加质量作用下，水中叶轮固有频率显著低于空气中[4]；在阻尼作用下，振动系统的振幅逐渐衰减，阻尼越大，振动衰减越快[5]. 为定量评估水力机械可能存在的过度振动，需要考虑叶轮在水中的固有模态和阻尼特性[6].

在瑞士洛桑联邦理工大学高速水洞中，ROTH等[7]采用空泡溃灭产生的激波激励水翼，采用激光多普勒测振仪获取振动响应，得到静水中固有频率. YAO等[8]和SEELEY等[9]采用压电片激励水翼，得到0～20 m/s流速范围内的固有频率，结果表明其相对变化量在10%以内. LIANG等[10]通过实验和模拟分析了附加质量效应的影响表明水环境能够降低叶轮固有频率，但空气中和水中有相似振型. 基于声固耦合的模态分析方法，有学者[8,11]得到水翼在水中不同阶次的固有频率，与实验结果相比较，相对偏差在7%以内. TORRE等[12]采用类似方法，得到水翼在不同淹没深度下的固有频率，结果表明随着淹没深度的增大固有频率逐渐减小. LIU等[13]在不同空化条件下研究了水翼的固有频率特性，研究发现空化越严重时固有频率越高. WANG等[14-15]基于声固耦合方法研究发现，当工作介质发生变化时，水中声速改变，水下结构可能会产生一个新的振动模态. 前人研究多采用翼型代替叶轮进行研究，对于离心式叶轮，随着淹没深度的增加，模态振型是否发生改变目前尚不明确.

在水体压力、黏性和流动等作用下，振动系统在水中受到水体附加的阻尼力，进而降低振动系统的振动幅值[6]. 阻尼比特性与结构模态相关，已有研究表明，低阶模态的阻尼比更大[6]. 由于流固耦合作用的复杂性，目前水下结构的阻尼特性研究对象主要集中在圆柱[16]、薄板[17]及水翼[18]等简单结构，且主要针对低阶模态. 流体介质对阻尼特性影响显著，对于水翼一阶弯曲模态，有实验表明空化越严重，阻尼比越小[11]. 在方形水箱中，YOUNES等[19]晃动水体激励平板，并通过加速度传感器获取响应信号，基于对数衰减法识别阻尼比；实验结果表明水箱中水体越多时，减速度信号衰减速度越快. CHAPLIN等[16]基于实验得到圆柱在不同流动环境中的阻尼特性，研究发现动水中阻尼比显著大于静水中. 基于简化模型的理论推导[18]、实验[20]、双向流固耦合获取振动响应[5]及单向流固耦合计算结构做功[21]等方法，水翼与流速之间的线性变化关系已经被建立. 对于复杂结构，GAUTHIER等[21]基于单项流固耦合数值模拟，得到水轮机转轮一阶模态的阻尼比约为15%，然而没有相关实验数据进行验证.

在单一空气或者水环境中，叶轮结构固有频率的变化研究较多，但对其阻尼特性的关注相对较少[16-18]. 针对离心式叶轮，淹没深度与叶轮固有频率和阻尼之间的定量关系还不明确. 本文通过干湿模态分析和实验相结合的方法，探究了不同淹没深度下叶轮动力响应特性.

1 理论背景

1.1 振动方程

结构动力学方程可表示为[8]

(1)

(2)

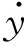
对于自由振动，求解式(1)后得振动方程为

y(t)=Ae-ζ ωntsin(ωd+φ)

(3)

(4)

式中：A为振幅；ωd为阻尼固有角频率；φ为相位.

1.2 模态分析理论

对于水中模态分析，假设流体无黏、不可压，且不考虑流动，水体压力可用声波方程表示为[10]

(5)

式中：p为水体压力；v为水中声速；t为时间.

将结构动力学方程与方程(5)耦合，可表示为[10]

(6)

式中：Ms、Cs和Ks分别为结构的质量、阻尼和刚度矩阵；Mf、Cf和Kf分别为水体附加的质量、阻尼和刚度矩阵；Mfs和Kfs分别为耦合系统的质量和刚度矩阵.

1.3 其他参数定义

在后处理分析时，不考虑水体附加刚度，水体附加质量系数可表示为[11]

(7)

式中：ms和mf分别为叶轮模态质量和水体附加质量；fna和fnw分别叶轮在空气中和水中的固有频率. 某阶模态下，叶轮总质量m包括结构模态质量ms和水体附加质量mf.

在不同淹没深度下，附加阻尼系数定义为

γ=(ζ-ζa)/ζa

(8)

式中ζa为空气中阻尼比.

将淹没深度量纲一化，定义相对淹没深度为

h*=h/φ2

(9)

式中：h为淹没深度；φ2为叶轮出口直径.

2 实验方案

2.1 实验台

实验模型如图1所示，在方形水箱中，将叶轮自由悬挂，加水使叶轮分别处于淹没深度为h=0(空气中)，47.5，95.0，147.5和190.0 mm(完全淹没)5种水深环境下. 采用力锤激励叶轮，通过NI采集卡获得加速度响应信号和力锤激励信号. 通过放大器对电荷信号放大，在处理器中运用LabVIEW和Matlab软件进行信号处理. 力锤型号为AD-YD-305，灵敏度3.9 pc/N，采样频率40 kHz. 采集卡型号为NI-9234，携带C系列声音与振动输入模块，量程为±5 V，共有4通道. 加速度传感器型号为AC135-2C/010M，灵敏度为500 mV/g，采样频率为25.6 kHz.

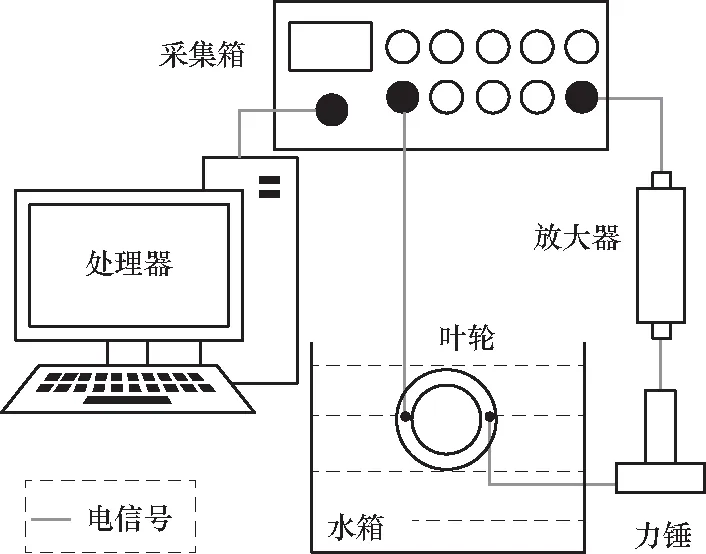
图1 实验台示意图Fig.1 Schematic of the test rig

电荷放大器型号为1NV1841，1通道恒流电荷输入和输出，通带范围为0.3～50 Hz. 玻璃水箱长宽高分别为500，500和600 mm，玻璃厚度为12 mm.

2.2 实验叶轮

实验对象为单级单吸离心式叶轮，比转速为52.6. 进口直径45 mm，出口直径为190 mm，叶片数为5，具体参数如图2所示. 叶轮材料为铸铁，密度7 300 kg/m3，弹性模量155 GPa，泊松比0.29.

图2 叶轮模型Fig.2 Physical model of impeller

2.3 测点位置

实验采用两种测点布置方式，第一种为单点激励、多点拾取的方法，测点布置如图3(a)所示. 第二种为采用单点激励、单点拾取的方法，测点布置如图3(b)所示.

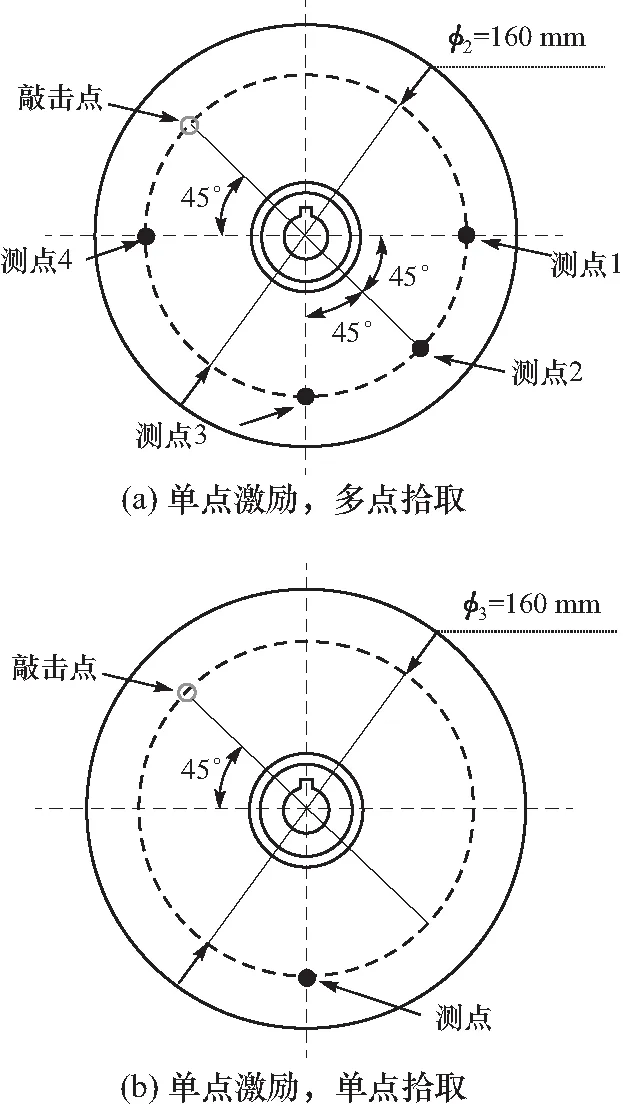
图3 激励点及测点示意图Fig.3 Schematic of the incentive and measuring points

3 结果与讨论

3.1 模态分析

3.1.1网格及计算设置

叶轮及流体网格如图4所示，叶轮与流体相接触部分设置为流固耦合面，水体与空气间接触面设为自由液面，其他边界为刚性壁面.

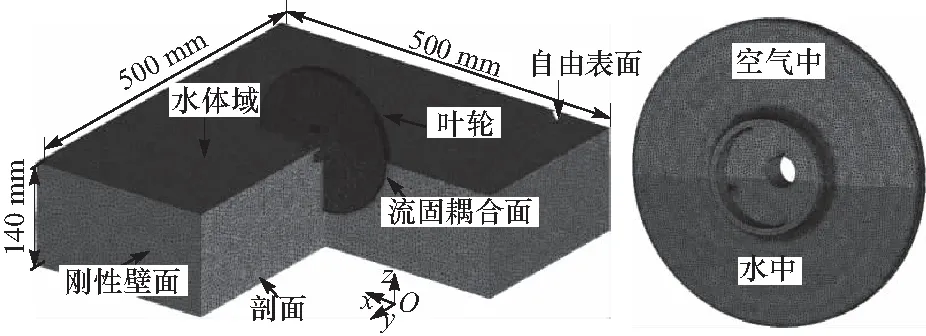
图4 网格及边界条件，h=95 mmFig.4 Mesh and boundary condition，h=95 mm

以前三阶模态固有频率为关键参数，进行网格无关性检查，如图5所示. 模拟结果表明，当叶轮网格单元数从16万增加到27万时，第一阶、第二阶和第三阶模态固有频率变化量分别为1.81%、1.78%和0.65%.

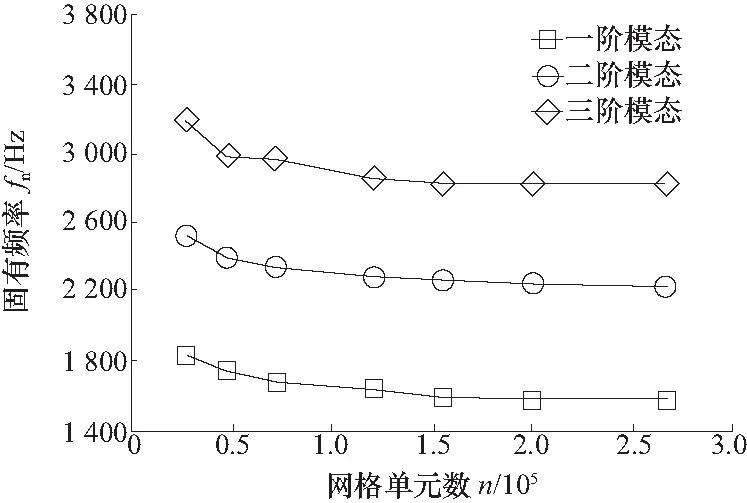
图5 网格单元无关性检查Fig.5 Mesh elements independent analysis

3.1.2振型及固有频率

叶轮第一阶模态振型如图6(a)所示，图中有2条线位移值为0，4个大变形发生在叶轮出口，且相邻间隔约为90°，该模态为典型二节径振型. 对于第二阶模态，5个大变形发生在叶轮出口边，振型图中有一个位移为0的圆，该模态为一节圆振型. 对于第三阶模态，6个大变形发生在出口边，振型图中有3条位移为0的线，该模态为三节径振型.

图6 模态振型，h=190 mmFig.6 Mode shapes，h=190 mm

不同淹没深度下固有频率如表1所示，结果表明，随着淹没深度的增大，固有频率逐渐较小. 在空气中和不同淹没深度的水中，相同阶次模态的振型相一致.

表1 不同淹没深度下前三阶模态固有频率，模态分析

3.2 实验结果

在不同深度，对同一测点反复敲击30次，并对动态响应信号数据进行分析处理.h=47.5 mm时，带通滤波前后振动响应分别如图7(a)和7(b)所示. 基于快速傅里叶变换，得到响应信号频域图，如图7(c)所示. 滤波前频域图存在多阶频率成分，将模态分析前三阶固有频率与实验结果相比较，相对偏差分别为0.68%、9.57%和2.32%. 频域结果表明，第一阶模态响应幅值显著高于其他阶模态. 滤波处理后，响应信号频率成分仅保留第一阶模态固有频率.

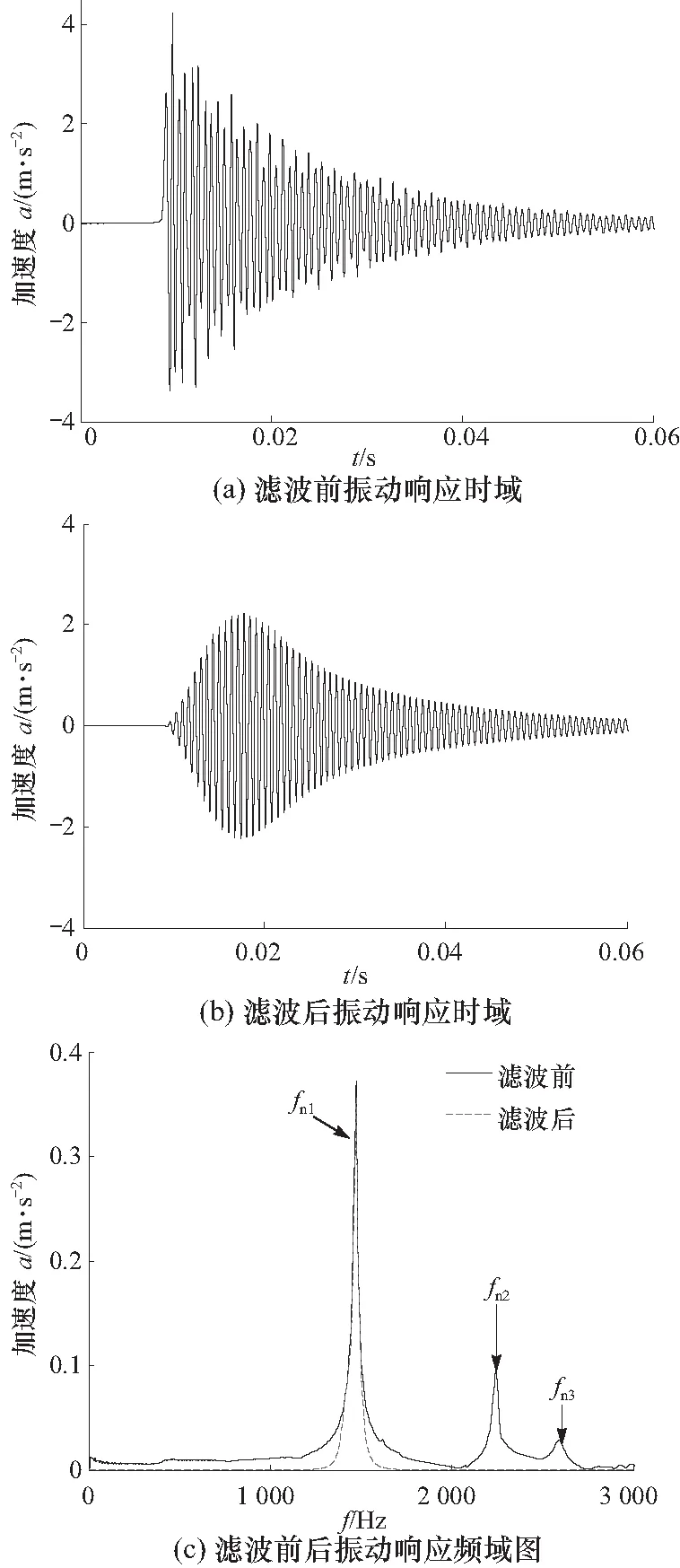
图7 带通滤波前后响应信号，h=47.5 mmFig.7 Response signal before and after filtering,h=47.5 mm

3.2.1测点无关性分析

在空气中和完全淹没环境下，以固有频率和阻尼比为关键参数，进行测点位置无关性检查. 在空气中和水中，不同测点得到的固有频率表2所示，最大相对偏差分别为1.42%和2.46%. 在空气中和水中，不同测点得到的阻尼比如表3所示，最大相对偏差分别为3.63%和4.78%. 实验结果表明，测点对响应信号的固有频率和阻尼特性无显著影响; 在不同淹没深度进行实验时，采用单点激励、单点拾取的测点布置方法.

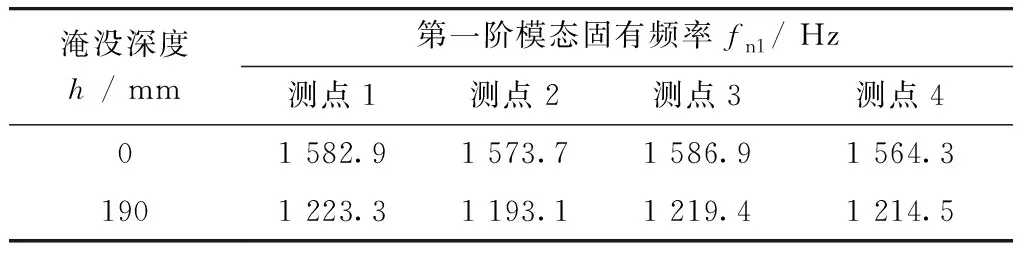
表2 不同测点固有频率Tab.2 Natural frequencies in different monitoring points

表3 不同测点阻尼比Tab.3 Damping ratios in different monitoring points

3.2.2附加质量

不同淹没深度h下，基于模拟和实验得到第一阶模态的固有频率如图8所示.h=0,190 mm时，固有频率相对偏差分别为4.19%和5.69%. 随着淹没深度增加，固有频率线性减小规律保持一致.

图8 不同淹没深度下模拟及实验固有频率Fig.8 Natural frequencies under different submerged depths, simulation vs. experiment

基于实验结果，根据式(7)，得到不同淹没深度下第一阶模态的水体附加质量系数，如图9所示. 结果表明，附加质量系数随淹没深度线性增大，拟合函数可表示为λ=0.39h*. 完全淹没时，水体附加质量为0.39倍的空气中叶轮模态质量.

图9 不同淹没深度下附加质量系数Fig.9 Added mass coefficients under different submerged depths

3.2.3阻尼比

当淹没深度h=0，95和190 mm时，滤波处理后的响应信号分别如图10(a)～10(c)所示. 在阻尼作用下，振动幅值随阻尼逐渐衰减，且淹没深度越大，振幅衰减的速度越快. 找到响应信号所有上峰值点后，根据式(3)，在Matlab中进行函数拟合，得到不同淹没深度下的阻尼比.

图10 不同淹没深度下响应信号Fig.10 Response signals under different submerged depths

不同淹没深度下，叶轮第一阶模态的阻尼比如图11所示，实验结果表明，随着淹没深度的增加，水体对叶轮的黏性阻滞效应越明显，阻尼比线性增长，拟合函数可表示为ζ=0.009 7h*+0.005 6. 为定量表示淹没深度对阻尼比的影响程度，根据式(8)计算附加阻尼系数. 随着淹没深度增大，附加阻尼系数线性增大，拟合函数可表示为γ=1.8h*. 完全淹没时，水体附加阻尼比为1.76倍的空气中叶轮阻尼比.

图11 不同淹没深度下阻尼比Fig.11 Damping ratios under different submerged depths

图12 不同淹没深度下的附加阻尼系数Fig.12 Added damping coefficients under different submerged depths

4 结 论

基于实验和数值模拟方法，定量分析了不同淹没深度下，叶轮固有频率及阻尼比的变化特性，主要结论如下所示：

① 模拟结果与实验结果吻合良好，不同淹没深度下第一阶模态固有频率的相对偏差在5.69%以内，振型不随淹没深度发生改变.

② 附加质量系数随相对淹没深度线性增大，完全淹没时，水体附加质量为空气中的0.39倍.

③ 附加阻尼系数随相对淹没深度线性增长，完全淹没时，水体附加阻尼比为空气中的1.76倍.