宽幅斜拉桥钢箱加劲梁空间变形分析

唐 钒，杨永清，何灵芝

（西南交通大学 土木工程学院，四川 成都 610031）

随着我国现代交通运输的需求扩大，近年来大量桥梁在我国黄河、长江及海湾的交通大动脉上相继建成，成为了沟通两地的交通枢纽。其中大跨径超宽幅的桥梁结构被广泛运用于桥梁设计中。斜拉桥因其具有较小的梁体内弯矩，较低的建筑高度，较轻的结构自重，良好的跨越能力，以及优美的造型等优势，在桥梁设计中占有相当大的比重。

近年来许多学者也对斜拉桥空间力学性能进行了不同程度的研究，有学者展开了对超宽混凝土主梁斜拉桥的空间受力的分析工作，还有学者对宽幅钢箱加劲梁斜拉桥的空间行为进行了数值分析，着重分析了该桥钢箱加劲梁部分的横向变形。为了进一步研究大跨径超宽幅斜拉桥钢箱加劲梁（以下简称“钢箱梁”）的受力特点，本文结合某宽幅斜拉桥，采用ANSYS 建立有限元节段模型，进行静力计算分析，为同类型结构的桥梁提供一定的设计参考。

1工程背景

某宽幅斜拉桥跨越某水道，该水道水面宽度2350m 左右，测时最大水深为9.5m，线路与水流方向夹角为84°。为了满足其通航要求，选取设计方案为主跨3×340m，主桥采用58.5m＋116m＋3×340m＋116m＋58.5m 斜拉桥，全桥立面图如图1 所示。公铁平层布置、桥塔中置，中间钢箱梁可通行双向两车道铁路列车、两侧钢挑臂梁可承受双向十车道公路荷载，桥面采用正交异性钢桥面板结构形式。

图1 全桥立面图（单位：m）

该宽幅钢箱梁顶宽49.6m，底宽17.6m，挑臂长16.0m，梁高4.676m（横截面）。钢箱梁横截面如图2 所示。公轨两用大挑臂钢箱梁是一种较新颖的结构形式，在既有设计规范中少有涉及，其纵、横向受力状况不同于一般箱型结构。因此，通过有限元理论分析，研究其静力力学性能是非常有必要的。

图2 车辆活载作用下钢箱梁横截面构造图（单位：cm）

2 有限元模型及计算工况

2.1 有限元模型

本文采用大型有限元软件ANSYS，从跨中点向右取60m 节段，对该节段钢箱梁进行精细化建模。该节段侧面图如图3 所示。建模时考虑到所研究结构的大部分板件均为薄膜，且由于结构的复杂性，在分析过程中可能会出现大转动的非线性变化，因此选择空间板壳单元shell181 进行模拟具有一定的适用性。拉索由于仅承受轴向的拉压且节点只有平向自由度，因此采用3D 杆即link8 空间杆系单元模拟。节段模型共计556132 个节点，596665 个空间板壳单元，10 个空间杆系单元。节段模型与桥塔相接的端部位置采用固结模拟，另一端通过施加集中力模拟成桥状态节段受力。结构自重由软件根据材料特性及用量自动计算，通过施加竖向均布荷载模拟二期恒载，按照331kN/m 进行模拟加载。通过单元选择活载作用范围并施加部分竖向均布荷载模拟汽车及火车活载。节段有限元模型如图4 所示。

图3 钢箱梁节段侧面图

图4 钢箱梁节段有限元模型图

2.2 计算工况

（1）工况1：自重+二期恒载+十车道汽车与列车双向车道全载。

（2）工况2：自重+二期恒载+十车道汽车与列车单向车道偏载（偏载均作用于梁节段右侧位置）。

3 空间变形

3.1 自重与二期恒载以及汽车列车位移全载作用下的空间变形

在成桥自重、二期恒载、索力汽车及列车双向车道全载的作用下，钢箱梁横向与纵向变形情况如下：

整体节段有限元位移结果如图5 所示，由于梁节段结构以及荷载分布均为对称，所以整体变形呈现对称分布，在梁端处挠度变化最大，挑臂端挠度变化明显大于两侧腹板之间的箱体区域。

图5 整体节段有限元位移结果图（单位：mm）

钢箱梁节段沿纵向中心线挠度变化如图6 所示，整体节段沿纵向为线性变化，钢箱梁节段中间截面横向挠度变化如图7 所示，呈曲线变化趋势。

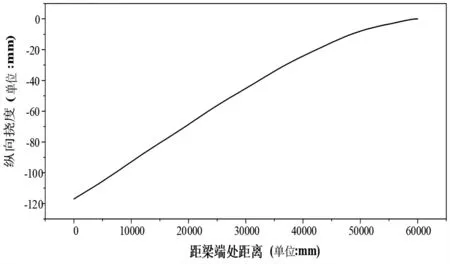
图6 全载作用下钢箱梁节段沿纵向中心线位移图

图7 全载作用下钢箱梁中间截面横向位移图

在全载作用下钢箱梁节段整体纵向变形呈现整体线性下挠趋势，由于右侧梁端固结，所以基本无位移，最大挠度出现在左侧梁端位置，最大值为118.60mm。

在全载作用下钢箱梁中间截面位置处最大挠度出现在截面左右两侧挑臂端，最大值为79.45mm 下挠。两侧外腹板之间挠度变化不明显，从两侧外腹板到挑臂的结构位置空间变形较为明显，呈不断下挠的趋势，挠度变化从45.03mm 到79.45mm。整体中间截面整体的横向位移呈现对称分布。

3.2 自重与二期恒载以及汽车列车单向偏载作用下的空间变形

在成桥自重、二期恒载、索力、汽车以及列车单向车道偏载的作用下，钢箱梁横向与纵向变形情况如下：

钢箱梁节段有限元计算结果如图8 所示，由于是偏载作用，整体挠度为不对称分布，偏载作用侧挠度远大于无偏载作用侧。偏载作用处的右侧挑臂端挠度幅度最大，越远离偏载作用侧挠度变化越小，越靠近固结梁端处的挠度变化越小。最大竖向挠度出现在梁端右侧挑臂位置，最大值为121.66mm。

图8 钢箱梁节段有限元位移结果图（单位：mm）

钢箱梁节段沿纵向中心线挠度变化如图9 所示，整体节段沿纵向为线性变化。钢箱梁节段中间截面横向挠度如图10 所示，为不对称曲线。在偏载工况的作用下钢箱梁节段沿着纵向中心线呈现下挠趋势，右侧梁端固结，基本无位移趋势，沿中心线最大挠度出现在左侧梁端位置，最大值为64.27mm。

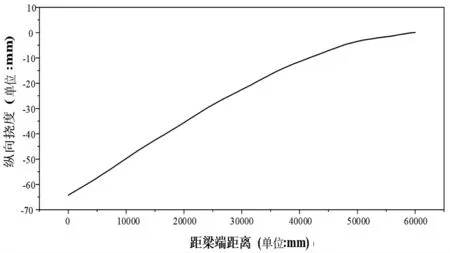
图9 偏载作用下钢箱梁节段沿纵向中心线位移图

图10 偏载作用下钢箱梁中间截面横向位移图

在偏载工况的作用下钢箱梁节段沿着纵向中心线呈现下挠趋势，右侧梁端固结，基本无位移趋势，沿中心线最大挠度出现在左侧梁端位置，最大值为64.27mm。

在偏载工况的作用下钢箱梁节段中间截面挠度为不对称分布，左侧无偏载工况作用处挠度基本无变化且很小，靠近截面中心处挠度开始逐渐变大。右侧偏载工况作用处结构竖向变形较为明显，呈不断下挠的趋势，并在右侧挑臂达到最大值93.27mm。

4 结论

本文基于有限元分析软件ANSYS 对某60m 宽幅斜拉桥节段模型进行了挠度计算，通过对施加汽车与火车全载与偏载两种不同的荷载工况对节段结构变形进行了详细分析，得到如下几点结论，可以为以后同等结构的桥梁提供参考。

（1）在全载工况的作用下，从整体结构纵向来看悬臂梁端的变形最大，从单一横向截面来看，在两侧外腹板之间挠度变化不明显，往外越靠近挑臂端挠度变化越大，且在挑臂端部附近达到最大值。在对称荷载作用下整体变形情况分布趋于对称。

（2）在偏载工况的作用下，偏载作用侧近悬臂梁端的挑臂位置变形最大，以此为局部中心挠度呈现分布为扇形分布，越远离中心挠度越小。

（3）不用的荷载作用对结构的空间变形有较大的影响。在两种荷载情况下，均可以看出在宽幅钢箱梁带挑臂的结构中，挑臂端的变形最为明显，腹板之间的节段变形不明显。