车用燃料电池空压机高速高温转子结构强度分析

张智明，潘佳琪，章 桐

（同济大学汽车学院，上海 201804）

现今车用燃料电池空压机不断向超高速化发展以满足大功率燃料电池系统空气供给需求，永磁同步电机的最高转速已达10万转，甚至接近20万转。增加转子转速是保证空压机在小体积、轻质量的同时实现高压比、大流量供气的关键途径［1］。

转子永磁体在高转速时会承受极大的离心力，而高速电机与叶轮的一体化设计导致较高温升［2］。离心力和温升会增大转子所受的应力，尤其是转轴上表贴式的钕铁硼永磁体材料，其具有较低的抗拉强度，需要设置大过盈量配合护套加以保护。但较大过盈量又会导致装配困难和护套强度的不足。王继强等［3］研究了转子和永磁体强度问题，计算了不同过盈量下的永磁体应力。结果表明，轴向装配预压应力会使永磁体两端的轴向应力大于中部。陈亮亮等［4］研究了护套厚度和静态过盈量对转子强度的影响，并对比热态和冷态两种情况下的各向应力。结果表明，温升会显著提高永磁体拉应力和护套的等效应力。张凤阁等［5］用三维有限元模型对冷态和热态运行时转子强度进行了分析和验证，并对考虑弯曲应力的碳纤维护套进行了设计和计算。陈家新等［6］综合考虑转速、温升、永磁体抗拉强度等影响因素，给出了永磁体与护套间过盈量的计算方法。吴震宇等［7］提出一种综合考虑机械强度限制和电磁性能限制的表贴式转子优化设计方法，并发现护套材料热膨胀系数的不同会影响应力变化。Wang等［8］采用三维有限元模型对三层复合材料转子进行了有限元分析，提出了高速过盈配合转子的设计准则。李振平等［9］通过热-结构耦合强度计算分析了护套与永磁体间的过盈量。研究结果表明，转子强度由永磁体与护套间的动态过盈量决定，该值受到静态过盈量、高转速时位移及热位移三项因素影响。张超等［10］基于厚壁圆筒理论推导了考虑轴向应力和温度的合金护套应力解析计算方法，并用有限元法验证了计算结果的准确性。刘威等［11］对某一高速永磁电机碳纤维护套转子的模态、强度和温度场分别进行了研究，提出的设计方案应能充分满足各项性能要求。杨振中等［12］研究了使用碳纤维护套时转子的受力，分析计算了不同过盈量的影响。结果显示，过盈量小于一定值时永磁体与转轴分离出现打滑，而大于一定值后护套和永磁体所受的应力将急速增长，因而存在一个合适的取值范围。马振杰［13］分析了温度和转速对转子应力的影响。结果表明，护套与永磁体的应力均会随着两者的提升而增大。但护套应力主要受温度的影响，而永磁体应力主要受转速的影响。

为保证空压机运行的安全性，必须对转子永磁体与护套部件所受的应力极值进行校核。而从上述文献可以看出，已有的研究大多仅从单一影响因素着手进行分析，也未能通过定量计算分析出应力与影响因素间的函数关联，无法预测优化方案的有效性。因此，本文以一台100 000 r·min-1的燃料电池车用离心式空压机转子为研究对象，建立有限元模型。分析护套与永磁体间的过盈量、护套厚度以及转轴空心孔径等关键设计参数对转子受力的影响，建立应力极值与过盈量间的函数拟合关系式。基于燃料电池空压机超高速运行过程，分析转子在热态工况下的受力。最后，针对转子非均匀温度场作用，评估了轴向温差对转子关键部件结构强度的影响。

1 结构参数影响分析

1.1 转子结构和材料属性

空压机转子主要由转轴、永磁体和护套3部分组成。永磁体采用表贴式结构，胶合在转轴外表面，永磁体外侧设置了过盈配合的护套加以保护。转轴为阶梯轴结构，且中间开有尺寸较大的空心孔以减轻转轴质量，提升转子稳定性。实际转轴由多个部件组装而成以便于加工和装配，但鉴于这些部件材料相同且安装牢固，因此在建模中将转轴作为整体处理。转轴的上下两端并非完全对称，但对于轴心线呈旋转对称。转子的简化结构示意图和二维轴对称有限元模型如图1所示，材料性能参数如表1所示。

表1 材料性能参数Tab.1 Material parameters

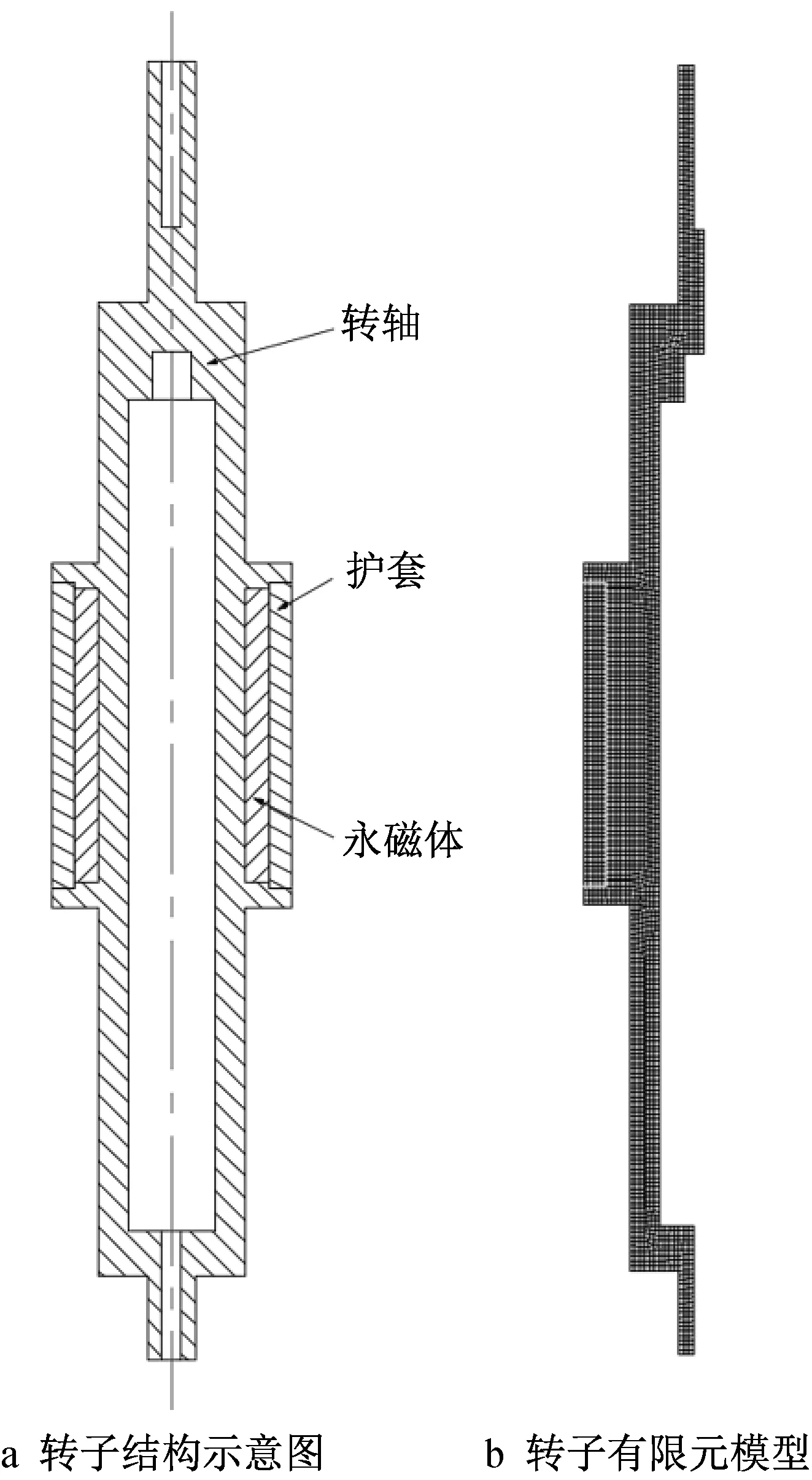
图1 转子结构示意图及其有限元模型Fig.1 Schematic diagram of rotor structure and finite element model

转子中心轴线上设置轴对称约束；在两端轴承安装位置的中点设置径向位移约束和全位移约束模拟轴承作用；在护套与永磁体的接触线上添加接触单元以设置初始过盈量；最后加载与工作转速对应的绕轴角速度。

1.2 过盈量

永磁体由护套以过盈配合施加预压应力，但其反作用力会使护套等效应力增加。因此过盈量取值对转子的整体强度尤为重要。在强度校核中永磁体为脆性材料，应采用第一强度理论校核拉应力。而护套和转轴为塑性材料，应采用第四强度理论校核。选取工作转速100 000 r·min-1，过盈量以0.01 mm为间隔从0.05 mm递增至0.15 mm，永磁体、护套和转轴在不同过盈量时所受的应力极值如表2所示。

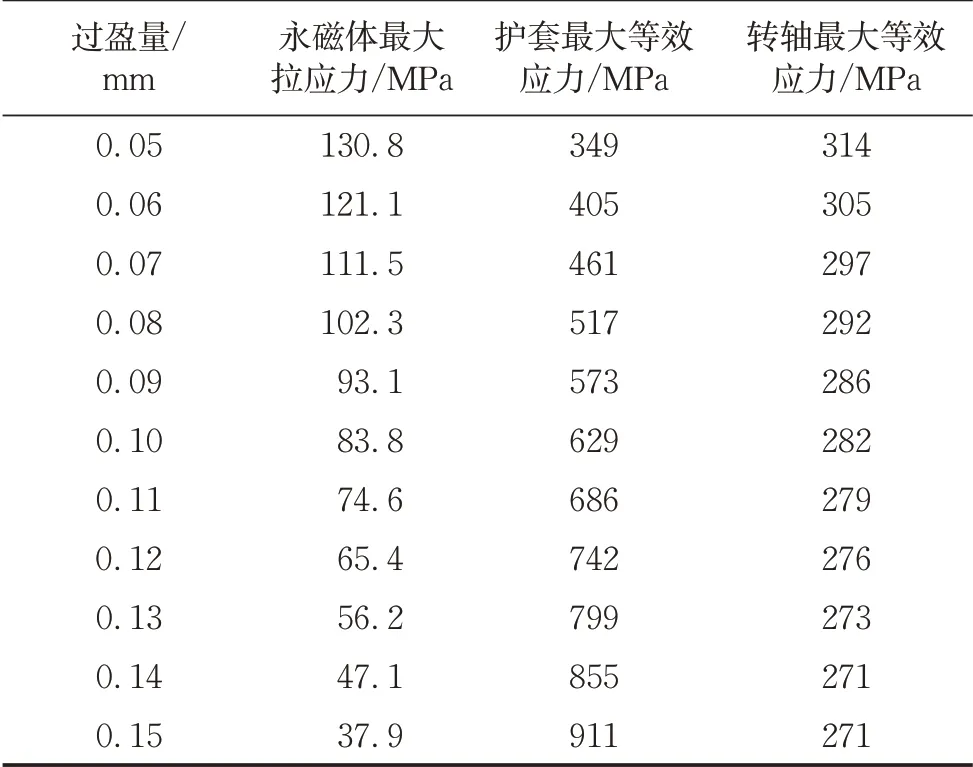
表2 不同过盈量时的应力极值Tab.2 Stress extremum at different interferences

对比表2中永磁体、护套和转轴的最大应力与表1中的强度极限值可以看出，当过盈量小于0.08 mm时，永磁体将发生破坏，而过盈量大于0.14 mm后，护套将发生破坏，转轴则不存在强度问题。因此过盈量取值应在0.08～0.14 mm之间。随着过盈量的增大，永磁体拉应力极值线性降低，护套等效应力极值线性提升。两者与过盈量间的拟合关系式为

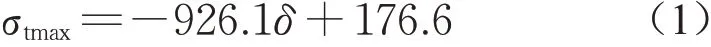
式中：σtmax为永磁体拉应力极值，MPa；δ为过盈量，mm。

式中：σseqv为护套等效应力极值，MPa。

从式（1）和式（2）可以看出，护套等效应力极值随过盈量的增长率远高于永磁体拉应力极值的降低率。所以采用大过盈配合保护永磁体时必须也要对护套应力进行校核，其强度决定了过盈量的取值上限。

1.3 护套厚度

护套厚度会影响转子变形和动态过盈量，也会影响永磁体和护套受力。以0.01 mm为间隔取过盈量为0.05～0.15 mm，以0.5 mm为间隔选取护套厚度为3.0～6.0 mm，并设置转速为100 000 r·min-1。永磁体拉应力极值的仿真结果如表3所示，护套等效应力极值的仿真结果如表4所示。

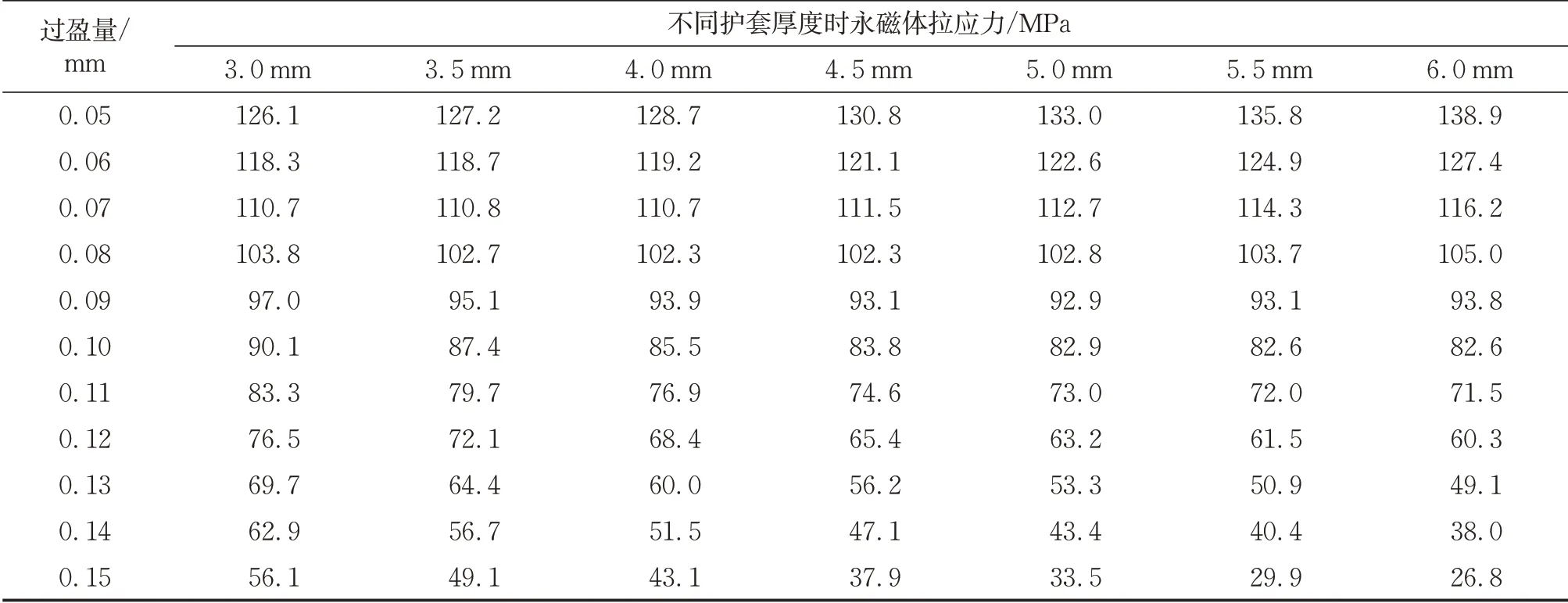
表3 不同过盈量和护套厚度时的永磁体拉应力极值Tab.3 Tensile stress extremum of permanent magnet at different interferences and sleeve thicknesses

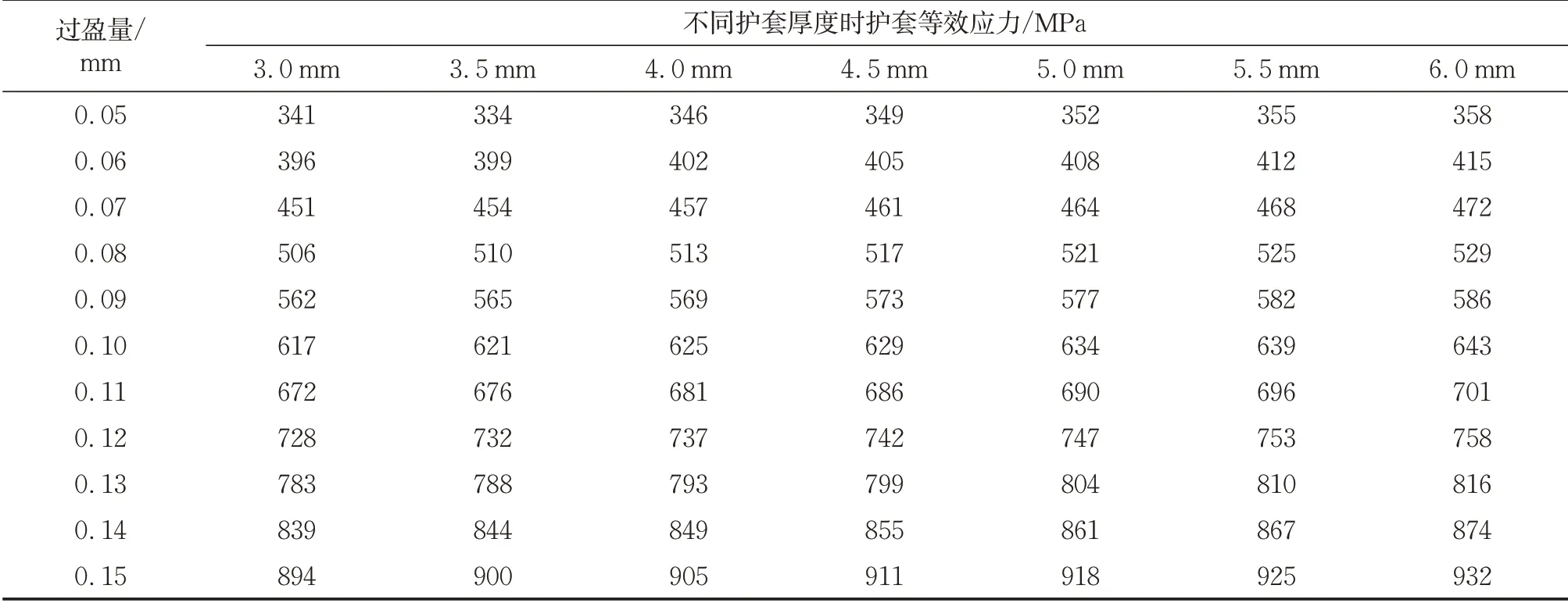
表4 不同过盈量和护套厚度时的护套等效应力极值Tab.4 Equivalent stress extremum of sleeve at different interferences and sleeve thicknesses

从表3的数据可知，不同护套厚度时永磁体拉应力极值均随着过盈量增大而线性降低，且护套厚度越大降低率越大。而护套厚度对永磁体拉应力的影响趋势取决于过盈量。考虑永磁体所受的拉应力需在强度极限以下，过盈量应大于0.08 mm。所以在满足强度要求的过盈量取值区间内，随护套厚度增加，永磁体所受的拉应力减小。且过盈量越大，增大护套厚度对永磁体拉应力的降低率也越高。护套从4.5 mm增厚至6.0 mm，过盈量为0.10、0.12和0.14 mm时拉应力分别降低了1.43%、7.80%和19.32%。因此，通过增大护套厚度降低永磁体拉应力时可适当增加过盈量以起到更好的保护作用。

此外，从表4可以看出，护套厚度对护套所受的等效应力极值影响很小，仅随护套厚度的增加有小幅增长。这是由于等效应力极值出现在护套内径处且主要由过盈装配引起，而增大护套厚度增加了护套外径。当护套厚度从4.5 mm增厚至6.0 mm时，护套等效应力增幅仅从2.1%升至2.6%。反之，减小护套厚度对护套强度的削弱也较小。

综上可知，增大护套厚度有利于降低永磁体所受拉应力，且仅使护套所受的等效应力有不到3%的小幅提升。因此，同时增加过盈量和护套厚度会更有利于提升转子的整体强度。

1.4 空心孔孔径

图1中转子的空心孔内径18 mm，长170 mm。该转子空心孔设计能够提升转子的临界转速，但也会降低转子的结构强度。以0.5 mm为间隔将空心孔半径从9 mm减小至5 mm，并取过盈量为0.08、0.10和0.12 mm。仿真计算所得的永磁体拉应力和护套等效应力极值分别如表5和表6所示。

从表5和表6中数据可以看出，永磁体拉应力和护套等效应力均随着转轴空心孔半径的减小而降低，减小转轴空心孔半径有利于转子整体强度的提升。进行定量计算可知，当空心孔半径减小至5 mm后，永磁体拉应力相比9 mm时降幅达34.4%至37.6%，且幅度随过盈量的增大略有提升。而护套等效应力降幅为2.0%至3.5%，且过盈量越大降幅越小。由此可见，减小空心孔半径对于降低永磁体所受拉应力十分显著。此外，减小空心孔孔径时，永磁体拉应力的降低率会随着过盈量的增加有小幅提升，从0.08 mm时的34.4%增长为0.12 mm时的37.6%，与增厚护套需要在大过盈配合时才较为有效不同。因此，减小空心孔孔径能够在选用低过盈量的同时对永磁体起到很好的保护作用。

表5 空心孔半径在不同过盈量时的永磁体拉应力Tab.5 Tensile stress of permanent magnet at differ⁃ent interferences of hollow hole radius

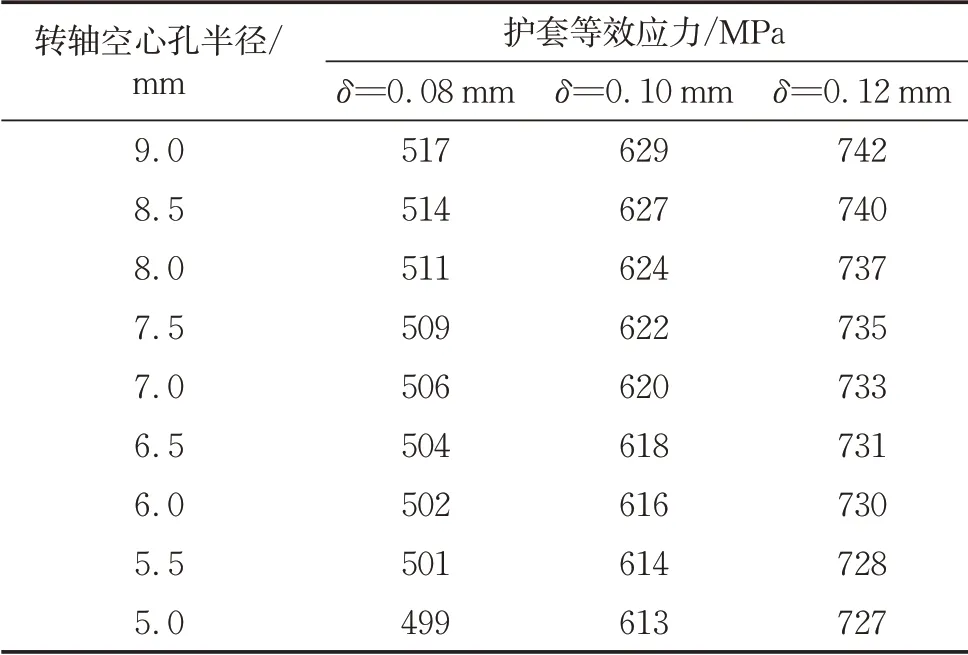
表6 空心孔半径在不同过盈量时的护套等效应力Tab.6 Equivalent stress of sleeve at different inter⁃ferences of hollow hole radius

2 温度影响的计算分析

2.1 均匀温度场

与驱动电机一体化设计的空压机转子在工作过程中有较高的温升，会在转子上产生额外的热应力。因此研究永磁体和护套在不同温度时的受力，并找出转子的最高工作温度对转子冷却设计十分关键。

环境温度为20℃，以10℃为间隔提升转子温度至120℃。设置过盈量为0.11 mm，工作转速时的应力极值如表7所示。

表7 不同温度时的永磁体与护套应力Tab.7 Permanent magnet and sleeve stress at different temperatures

从表7可以看出，永磁体拉应力极值和护套等效应力极值均随着温度的提升而增大。不过当温度从20℃升至120℃后，永磁体应力增长了124.0%，而护套应力只增长了5.0%。可见热应力对永磁体强度的影响远远大于护套。在温度超过60℃后永磁体就达到了强度极限105 MPa，而护套在120℃时仍满足强度要求。根据1.2节的结论可先通过增大过盈量来减小永磁体所受的拉应力，所得结果如表8所示。

从表8中的数据可以看出，当过盈量为0.12 mm和0.13 mm时，转子在70℃和80℃尚未达到强度极限105 MPa。而永磁体拉应力极值随温度的变化曲线可拟合为一元二次函数，由此推算永磁体将在72℃和83℃达到强度极限。但在过盈量达到0.14 mm时，护套在80℃时就先超过了强度极限，导致转子最高工作温度又有所降低。

表8 不同过盈量在不同温度时的永磁体与护套应力Tab.8 Permanent magnet and sleeve stress at dif⁃ferent temperatures with each interference

因而在考虑转子热态工况时应相比冷态工况增大过盈量的取值，可以有效提升转子的最高工作温度。但过盈量的提升会受到护套强度的限制，取值过大就会出现护套先达到强度极限的情况。此外，也可以看出单靠调整过盈量只能将转子的最高工作温度提升至83℃。因此还需要配合其他设计参数进行调整。

1.3节的研究结果表明，增大护套厚度有利于降低永磁体所受的拉应力。故取过盈量为0.13 mm，以0.5mm为间隔增大护套厚度至8.00 mm。不同护套厚度时的最高工作温度如表9所示。

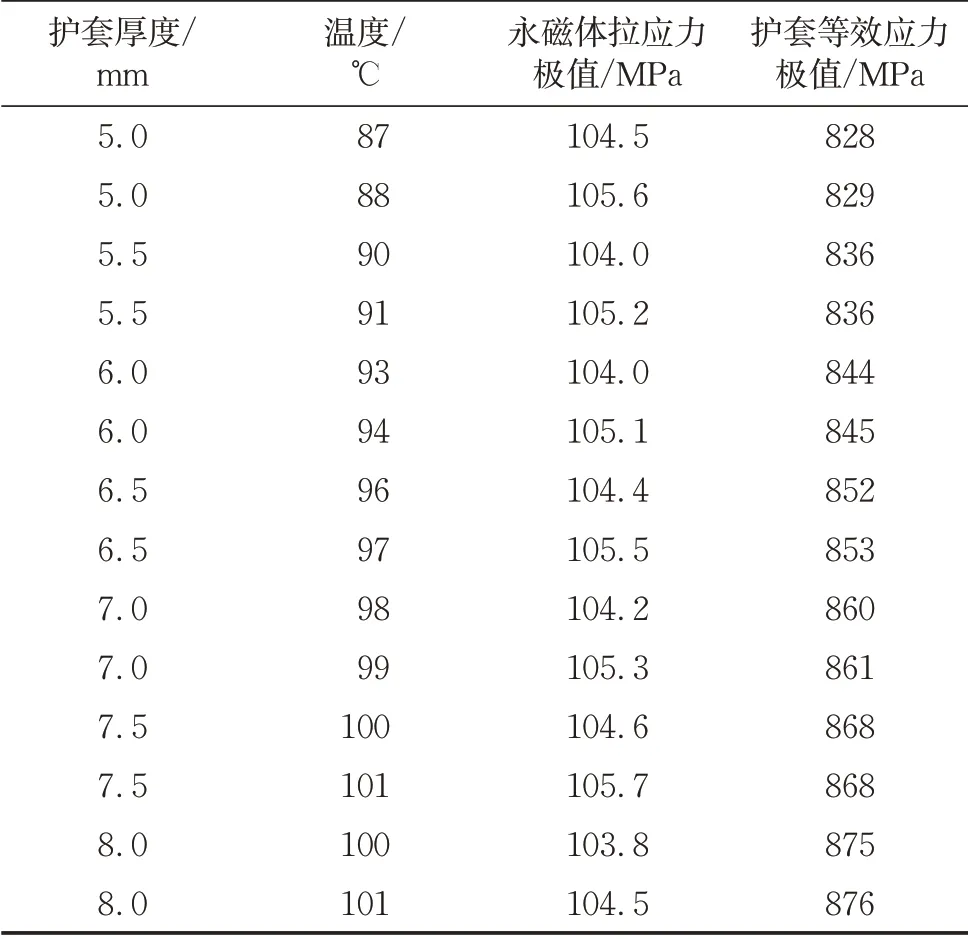
表9 不同护套厚度在不同温度时的永磁体与护套应力Tab.9 Permanent magnet and sleeve stress at dif⁃ferent temperatures with each sleeve thick⁃ness

由表8和表9可知，当护套厚度从4.5 mm增至8.0 mm时，转子的最高工作温度从原先的83℃分别增长至87、90、93、96、98和100℃。当护套厚度为8.0 mm时将转变为护套先于永磁体达到强度极限。因此增厚护套同样可以起到提升转子最高工作温度的作用，但同时也受护套强度极限的限制。

1.4 节的研究结果表明，减小转轴空心孔半径同样能起到降低永磁体拉应力极值的作用。故取过盈量为0.13 mm，以1 mm为间隔减小空心孔半径至5 mm。分析结果如表10所示。

表10 不同空心孔半径在不同温度时的永磁体与护套应力（过盈量0.13mm）Tab.10 Stress of permanent magnet and sleeve with each hollow hole radius at different temper⁃atures(interference 0.13mm)

由表8和表10可知，随着空心孔半径的减小，转子最高工作温度从原先的83℃分别增长至86、89、93和96℃。但由于减小空心孔半径可以同时减小护套所受等效应力，所以永磁体先达到强度极限，而护套离强度极限还有一定的裕量，可以进一步提升过盈量至0.14 mm。增大过盈量后的仿真结果如表11所示。

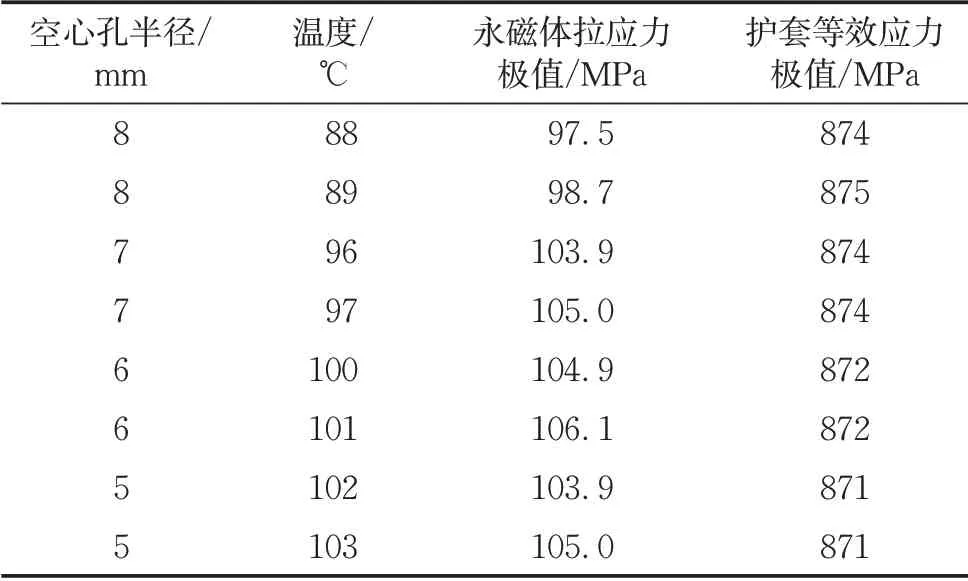
表11 不同空心孔半径在不同温度时的永磁体与护套应力（过盈量0.14mm）Tab.11 Stress of permanent magnet and sleeve with each hollow hole radius at different temper⁃atures(interference 0.14mm)

当过盈量提升至0.14 mm后，随空心孔半径的减小，转子最高工作温度进一步提升至88、96、100和102℃。可见，减小空心孔半径也能起到提升转子最高工作温度的作用，且效果还略优于增大护套厚度的优化方法。

综合以上两种方法，同时增大护套厚度并减小空心孔半径能使转子最高工作温度提升。将护套厚度增大至8.0 mm，空心孔半径减小至5.0 mm，过盈量取0.13 mm，当110℃时永磁体拉应力极值为104.8 MPa，护套等效应力极值为862 MPa。即通过结构优化可将转子的最高工作温度提升至110℃，降低转子冷却要求。

2.2 非均匀温度场

实际工作中空压机转子的一侧安装叶轮对空气进行增压，压缩空气时产生的热量会使转子在靠叶轮端的温度高于另一端，因而转子会在轴向存在较大温差。由于转子安装在电机壳体内部难以直接测量温度，通常采用在两侧端盖处安装温度传感器，通过测量轴承位置的温度来预测转子的温度分布。故将采集温度施加在两端轴承位置处，并进行温度场分析，再将温度场分析的结果作为热载荷进行结构强度分析。

设置低温端温度为80℃，高温端温度为100℃。永磁体和护套上的温度分布如图2所示，应力云图如图3所示。

图2 永磁体和护套的温度分布（单位：℃）Fig.2 Temperature distribution of permanent mag⁃net and sleeve(unit:℃)

图3 永磁体和护套的应力云图（单位：Pa）Fig.3 Stress nephogram of permanent magnet and sleeve(unit:Pa)

从图2可以看出，此时护套和永磁体上均出现了温度梯度，从高温端到低温端的温度逐渐降低。图4显示应力极值也出现在了靠近高温端的位置，但整体应力分布与均匀温度场时十分相似，基本呈两端对称。将转子整体温度设置为护套的最高温度94.73℃进行仿真计算，此时的应力分布如图4所示。

图4 均匀温度场的永磁体和护套应力云图（单位：Pa）Fig.4 Stress nephogram of permanent magnet and sleeve with uniform temperature field(unit:Pa)

对比图3和图4可以发现，护套和永磁体上的温度梯度只使应力最小值发生了明显变化，而最大值的计算结果相近。

再将低温端和高温端的温度分别设置为20℃和120℃，扩大温差进行仿真计算。可得此时护套最低温度和最高温度分别为67.49℃和93.66℃，永磁体和护套的最大应力分别为126.7 MPa和797 MPa。用护套最高温度93.66℃进行均匀温度场计算，可得此时永磁体和护套的最大应力分别为124.6 MPa和788 MPa，相对误差分别为1.66%和1.13%。可见，永磁体和护套所受的最大应力在存在温度梯度时几乎只取决于最高温度，而与低温侧温度的相关性很小。

因此，通过测量或仿真获取外侧护套在靠近叶轮安装端的最高温度，使用均匀温度场对护套和永磁体强度进行校核也具有足够的精度，无需再考虑实际温度场分布。此外，当转子轴向存在温度梯度时，由于应力极值受最高温度的影响，所以只有降低靠近叶轮的高温端温度才能更有效地避免永磁体或护套发生破坏，在空压机超高速转子冷却系统的设计中应当予以重视。

3 结论

本文通过有限元法对燃料电池离心式空压机超高速转子进行了结构强度校核，并从确保永磁体和护套的结构强度以及提升最高工作温度这两个角度出发研究了关键设计参数的影响，主要结论如下：

（1）在满足强度要求的过盈量取值区间内，永磁体拉应力随过盈量的增大而减小，护套等效应力变化趋势相反，而后者的变化率是前者的6倍。因此，护套强度决定了过盈量取值的上限。

（2）增大护套厚度和减小转轴空心孔半径可以减小永磁体拉应力，且不会使护套等效应力显著增大，能有效提升永磁体的强度，而后者作用更为显著。

（3）通过减小空心孔半径优化转子结构，并增大护套厚度可有效提升转子最高工作温度。

（4）当转子上存在轴向温差时，护套和永磁体的应力极值主要受最高温度的影响，因此，在冷却系统设计中应更关注靠近叶轮的高温端冷却问题。

作者贡献声明：

张智明：确定具体研究内容和建模仿真，指导论文撰写及修改。

潘佳琪：完成模型搭建及仿真，数据分析。

章 桐：提出研究目标，协助指导。