沿海典型大跨桥梁桥址区台风极端风荷载预测与应用

方根深，赵 林，卫苗苗，李 珂，葛耀君

（1.同济大学土木工程防灾国家重点实验室，上海 200092；2.同济大学桥梁结构抗风技术交通行业重点实验室，上海 200092；3.克莱姆森大学土木工程系，克莱姆森 29634；4.重庆大学山地城镇建设与新技术教育部重点实验室，重庆 400045）

台风（飓风、热带气旋）是一类快速旋转的中尺度低压涡旋天气系统，水平和竖向尺度约分别为100～2 000 km和15～20 km，通常形成于纬度大于5°的温暖洋面。台风一旦靠近大陆沿岸或直接登陆，不仅会造成巨大的经济损失和人员伤亡，还威胁沿海大跨度桥梁及建筑结构的安全。我国是台风多发区，每年约有7～8次台风直接登陆东南沿海，而该区域布局建造了大量大跨柔性桥梁。为满足我国沿海区域持续深化发展的建设需求，桥梁跨径已接近2 km甚至有可能达到5 km［1］，这类桥梁的抗风研究尤为重要，而确定桥位处的台风极端风荷载是关键环节［2-3］。

有别于季风、寒潮等全球性大尺度风气候，台风每年直接影响某一特定区域的概率通常很低，且强台风作用下，测风设备有时会发生损坏，无法完全捕捉最大风速，这使得气象站的实测台风风速样本有限，仅以该数据为母体样本来预测未来不同重现期的设计风速，误差普遍偏大。当前我国建筑结构荷载规范（GB 5009―2012）［4］和公路桥梁抗风设计规范（JTG/T 3360-01―2018）［5］推荐的设计风速是基于气象站实测数据估计的，而沿海地区气象站的风速样本包含了台风和非台风数据，两者对极值概率分布的贡献是不均匀的［6］，尤其是强台风风速样本会显著影响概率分布的尾部特征，造成估计的重现期极值风速与真实值偏差较大。因此，台风极值风速需采用随机模拟获取大量风速样本，开展单独预测。事实上，美国的ASCE规范［7］自ASCE 7―98版本就已经分别创建台风和非台风设计风速图，并基于统一风险（uniform risk）［8］的概念，提出了300、700、1 700和3 000年重现期的极值风荷载设计要求，以实现基于性能的工程设计目标［9］，而我国相关规范仍处于空白状态。

为实现台风快速模拟，工程应用多采用基于数理统计和适当简化的台风模拟算法［2，9］。首先基于历史数据的统计特征，采用随机模拟方法人工合成大量台风路径样本，然后将路径数据基本信息（包括中心位置、中心气压、风场参数、移动速度和前进方向等）输入台风风场模型，获取目标场地的台风风速样本，最后估计各重现期极值风速［10-12］。

本文基于日本气象局提供的1951年至2015年西北太平洋台风历史数据，建立台风路径、强度和风场参数随机模拟方法，并结合台风边界层三维风场模型，预测深中通道伶仃洋航道桥桥址处不同重现期、不同高度极值风速，并与现有规范结果进行比较。相应的台风极值风速模拟结果应用于伶仃洋航道桥的颤振可靠度分析，评估台风作用下大跨桥梁的颤振失效概率和安全性能。

1 台风随机模拟与极端风荷载预测

1.1 台风边界层风场解析模型

台风边界层作用在单位质量大气微团的力主要包括径向压力梯度力、重力、黏性力和地球自转科氏力，其动量守恒方程为

式中：v台风风速矢量；ρa为空气密度；p为气压；f为科氏力参数；k为竖向单位向量；g为重力加速度矢量；Fd为边界层中的黏性力；∇为Hamilton算子。

其中气压项采用参数化模型建模，表达如下［12］：

式中：prz为空间目标点气压；pcs为风中心气压；Δps为台风中心气压差；Rmax，s为最大风速半径；r为空间尺度坐标半径；Bs为Holland径向气压剖面形状参数；g为重力加速度；k为湿空气比气体常数与比定压热容的比值；z为垂直高度；Rd为干空气的比气体常数；θv为虚位温。

通过简化动力平衡方程，台风梯度层风速场可由下式求解：

式中：vTθ=-vTsin(θ-θT)，vT为台风移动速度，θ为目标点的角坐标，θT为台风移动方向与正东方的夹角，逆时针为正；f为科氏力参数；r为空间尺度坐标半径；ρg为梯度层空气密度；pg为梯度层气压。

采用尺度分析技术，可简化获取边界层径向和切向风速的解析解［9］为

1.2 台风随机模型

1.2.1 路径模型

台风路径模型通常采用台风移动速度vT和前进方向θT的递推公式描述，由vT和θT在每个时间步的数值确定下一个时间步台风风眼所在位置。传统采用局部圆形区域模拟法时，vT和θT的数值是根据圈选历史数据的母体概率分布随机采样的，而实际台风下一时间步前进方向和移动速度与上一时刻数值是统计相关的，这也是全路径模拟必须考虑的关键内容［10］。由此，一旦赋予台风移动的初始方向和速度，其接下来各时间步的vT和θT可由下式模拟：

式（6）、（7）中：aj和hj(j=1～4)为待定系数；vT(i)和θT(i)为时间步i的移动速度和前进方向；εΔlnvT和εΔθT为模型拟合偏差项。

1.2.2 强度模型

台风强度模型通常指台风中心气压的演变过程，包括在海洋洋面时的相对强度模型和登陆以后的强度衰减模型，其中海洋洋面的相对强度递推模型为［10］

式中：cj（j=1～6）为待定系数；I(i)和Ts(i)分别为第i个时间步的相对强度和海洋表面温度；εlnI为偏差项。相对强度是由台风中心气压、海平面温度和大气湿度定义的量纲一参数［11］，其中1951至1981年8月采用Hadley中心提供的月平均SST（海平面温度）数据资料（HadISST 1）［12］，之后的海平面温度由NOAA（美国国家海洋和大气管理局）提供的最优插值1/4°分辨率逐日海温再分析资料确定［13］。

台风一旦登陆，暖湿气流供应中断，台风中心气压会显著增大，强度迅速减弱而逐渐消散。多数情况下，沿海地区工程场地的最大风速出现在台风接近大陆沿岸和登陆过程中。准确刻画台风登陆衰减过程对预测沿海地区的设计风速尤为关键。常用的衰减模型可描述为登陆后前进距离或登陆时间的函数，本文采用台风中心压差随时间的指数衰减函数：

式中：t为台风登陆的持续时间；Δps0为即将登陆时的中心压差；a为登陆衰减率。

1.2.3 风场参数模型

式（2）中，风场关键参数Rmax，s和Bs需结合历史数据拟合并建立随机模型。本文基于日本气象局1977年至2015年提供的最佳路径数据，拟合获得了历史台风各时间步的Rmax，s和Bs，根据参数相关性分析结果，提出以下线性递推模型：

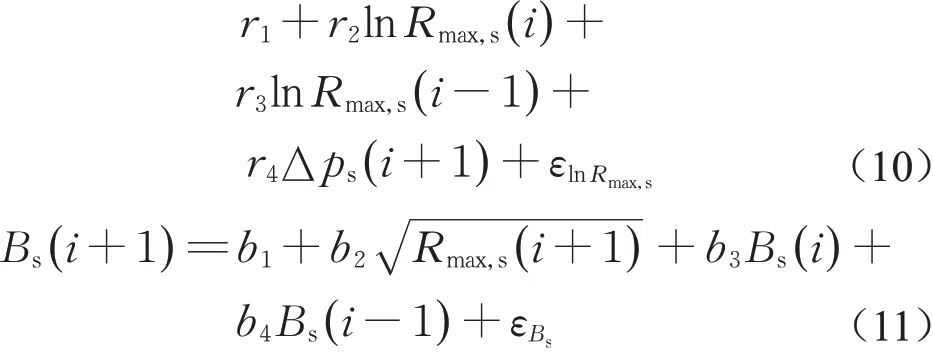
式（10）、（11）中：lnRmax，s(i)和Bs(i)为第i个时间步的数值；εlnRmax和εBs为模型误差项；r j(j=1～4)和bj(j=1～4)为待定系数。上述各模型的待定系数可采用地理加权回归方法获得。

1.3 极端风荷载预测

1.3.1 台风年极值风速预测

基于上述随机模型，可人工合成大量虚拟台风，包含了台风路径、中心气压、风场参数等基本信息，将这些基本参数输入台风边界层风场解析模型，即可计算所有台风历经目标场地时的风速，由此预测边界层内任意高度、不同重现期的年极值风速。假设每年影响该场地的台风数量相互独立，则T年内影响该场地的台风数量服从泊松分布，由此可计算任意T年内出现最大风速vi大于给定风速v的概率为

式中：N为vi大于v的台风数量；Y为模拟年数；风速v的重现期（return period，RP）即为上式T=1年时的倒数。

选取深中通道伶仃洋航道桥桥址（113.7454°E，22.4852°N）为目标场地，其中风场模型中地表粗糙长度z0可由桥位周边地貌近似确定。我国公路桥梁抗风设计规范［5］定义了海面、海岸和开阔水面的z0=0.01m，Davenport等［14］和美国规范ASCE 7―16［7］推 荐 开 阔 水 面 的z0=0.000 2m。实 际 上，Holthuijsen等［15］研究表明开阔水面的z0随风速先增大后趋于平稳或略有减小，真实的z0通常介于0.0002m和0.01m之间。本文将分别计算z0为0.000 2m和0.01m时的台风风灾曲线，近似认为真实风灾曲线位于两者之间。同时为了获取每次台风的最大风速，将时间间隔为6 h的模拟路径插值到15 min，而后计算每次台风风速时程。

台风路径模型包含全路径和局部圆形区域路径模型，在计算某特定场地的风速灾害曲线时，并不需要计算每次台风从生成到消散的整个风速时程，只需模拟以目标点为圆心、特定半径范围内的台风路径，以减小计算量。局部圆形半径的大小直接影响模拟结果，最佳模拟半径要求得到的风速灾害曲线不会随半径增大而产生显著变化。图1给出了基于局部圆形区域路径模型计算的伶仃洋航道桥桥址处z0=0.01m、10 m高度、10 min平均台风年极值风速v10重现期曲线。从图1可以看出，该曲线随着圆形区域半径增大而逐渐收敛，半径R为500 km的曲线与800 km的结果几乎重合，且百年一遇极值风速的差别小于0.2 m·s-1。因此，本文将选取半径为500 km开展模拟。

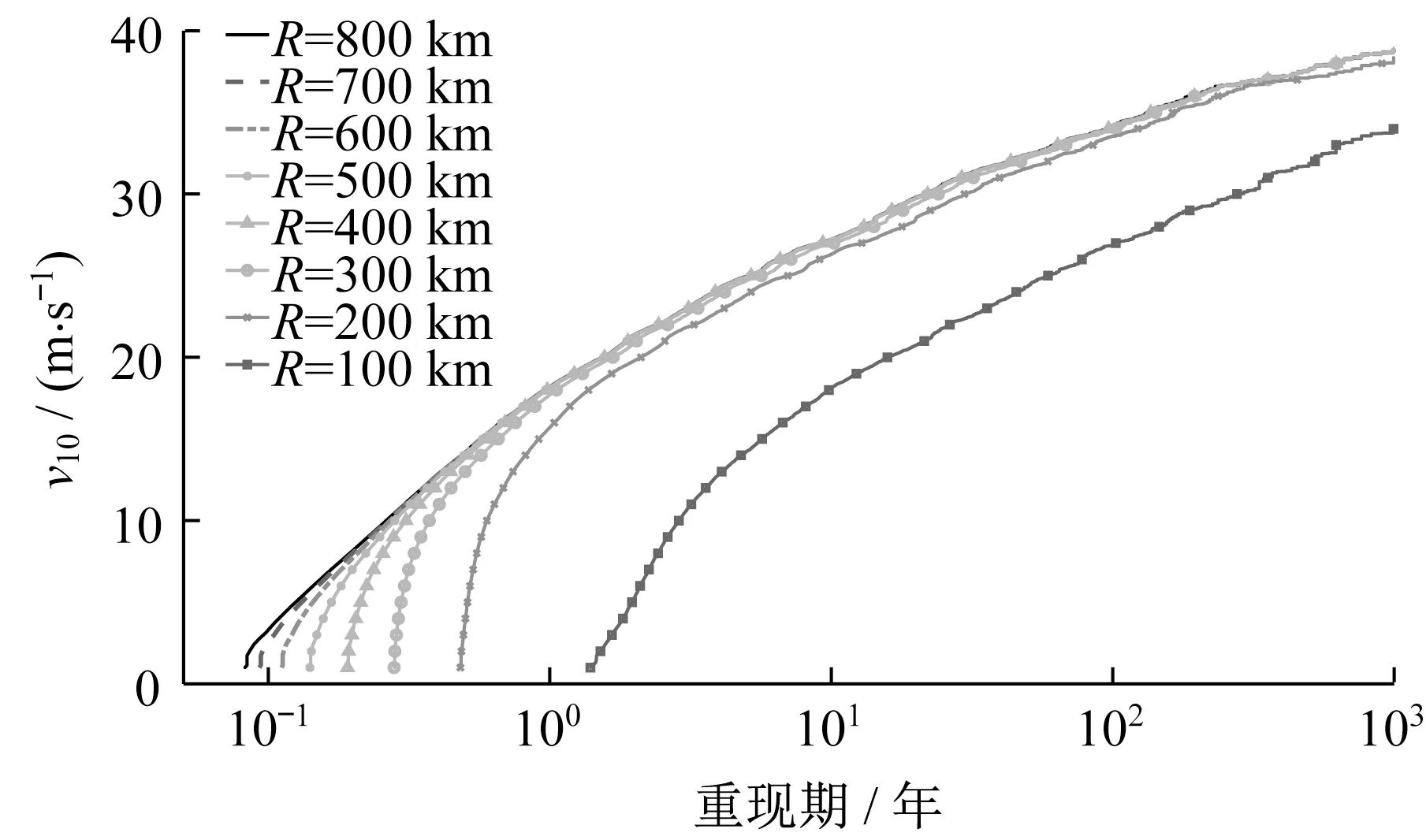
图1 圆形区域尺寸对风灾曲线的影响（10 m高度，10 min平均风速，z 0＝0.01 m）Fig.1 Influence of the size of the circular area on the wind hazard curve(10 m height,10 min average wind speed,z 0＝0.01 m)

1.3.2 风速灾害曲线

图2给出了伶仃洋航道桥桥址桥面高度（z=91.5m）、10 min平均年极值风速重现期曲线，其中模拟结果分别采用了10万年局域圆形区域法（CSM）和1万年全路径方法（FTM），同时给出了公路桥梁抗风设计规范（JTG/T 3360-01—2018）［5］推荐的中山和深圳的设计风速，该风速由设计基本风速（B类）根据指数率换算到A类地貌桥面高度。

图2 伶仃洋航道桥桥址处年极值风速重现期Fig.2 Annual extreme wind speed return period at the bridge site of Lingdingyang Bridge

从图2可以看出，当重现期约低于100年时，两种方法得到的年极值风速曲线基本重合，而当重现期进一步增大时，1万年全路径方法估计的风速值逐渐小于10万年局域圆形区域法的模拟结果，原因主要是由于用1万年的模拟数据估计超过100年重现期的年极值风速，样本容量往往不足，而局域圆形区域法获得的10万年样本，可更准确地估计长重现期的年极值风速。下文分析中将直接采用10万年局域圆形区域法模拟得到的结果。相比之下，由规范推荐的深圳设计风速接近z0=0.0002m的模拟结果，而中山设计风速则与z0=0.01m的模拟结果基本吻合；但规范推荐的重现期曲线较模拟结果更为平缓。规范结果主要根据极值分布拟合气象站点多年实测数据获得，而气象站不同来流方向的z0并不均匀，且极易受城市变迁的影响，在处理实测数据时难以实现地表粗糙度的准确修正；另一方面，实测数据包含了台风和非台风数据，虽然深圳和中山主要受台风控制，但非台风数据直接影响风速概率密度分布的尾部形状，从而影响重现期极值风速灾害曲线的变化趋势。

图3给出了对应的极值风速超越概率曲线，可根据式（12）直接计算获得，即任意T年内桥址处极值风速超越给定风速v的概率，可以看出，特定风速的超越概率随时间T增大而增大。通常情况下，风向垂直于大跨桥梁主梁轴向是最不利的，该结论同样适用于伶仃洋航道桥［16］。由此，图4给出了垂直于桥轴向极值风速vd，per的超越概率曲线，该极值风速并非只是图3分解到垂直于桥轴向的分量，而是由每次台风风速时程垂直于桥轴向分量的最大值组成。可以看出，考虑风向影响后，垂直于桥轴向极值风速的超越概率明显低于不考虑风向影响的结果。

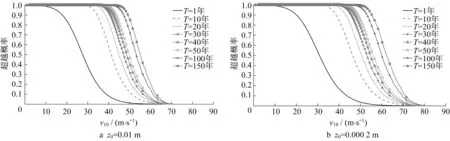
图3 伶仃洋航道桥桥址处极值风速超越概率Fig.3 Probability of extreme wind speed at the bridge site of Lingdingyang Bridge

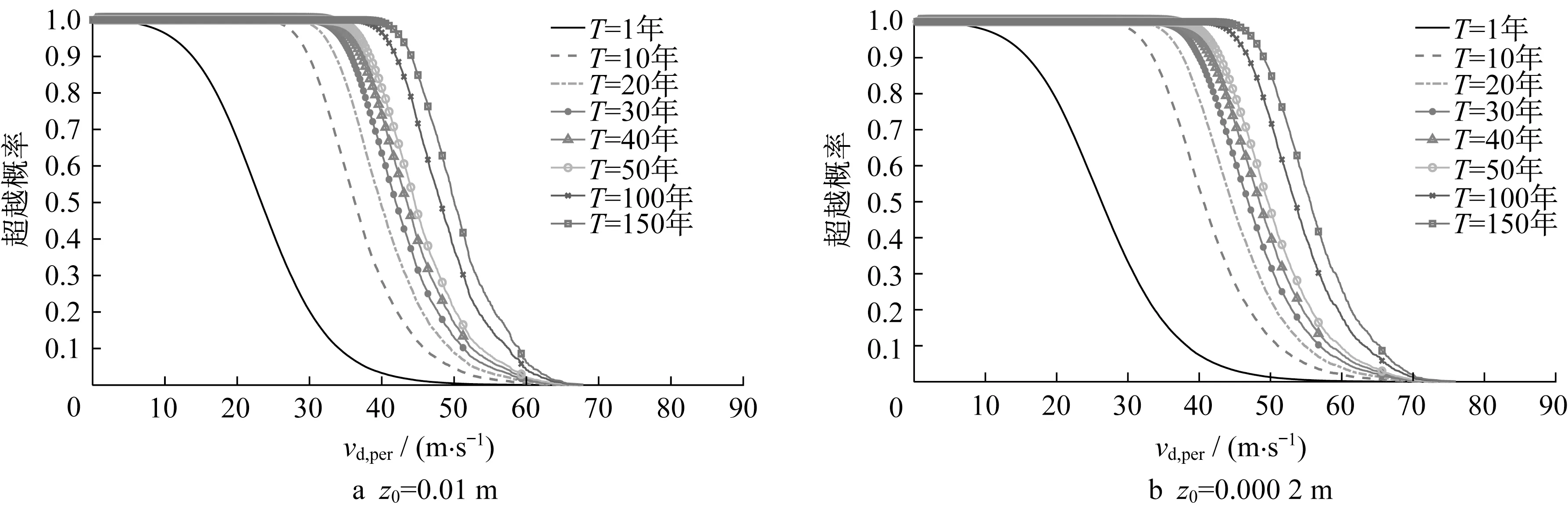
图4 伶仃洋航道桥桥址处（垂直于桥轴向）极值风速超越概率Fig.4 Probability of exceeding extreme wind speed at the bridge site of Lingdingyang Bridge(perpendicular to the bridge axis)

1.3.3 风速剖面

现有规范通常基于地表粗糙度界定风速剖面类型，而台风竖向风剖面不仅仅依赖于地表粗糙度，还受内部二次环流和气压梯度变化等影响，剖面形状有别于传统良态风。2.1节的台风风场模型可模拟边界层内任意高度的极值风速，由此，图5给出了两种地表粗糙长度（z0=0.01m和z0=0.0002m）对应的极值风速剖面图，并与规范A类地貌的指数率剖面做了对比。从图5可以看出，模拟得到的年极值风速随高度亦呈现指数率上升趋势，约在900 m以上趋于稳定，不同重现期的归一化风速剖面基本重合。z0=0.01m时模拟得到的台风极值风速归一化风剖面明显大于规范推荐的A类地貌（z0=0.01m，α0=0.12）的结果，即10 m高度基本风速相同时，模拟得到的台风极值风荷载显著大于规范建议值，而z0=0.0002m的归一化风剖面小于z0=0.01m的结果，但在300 m以下与规范A类地貌推荐剖面基本一致。由此可见，台风环境中，规范推荐的设计风荷载可能是不安全的，实际的台风极值风荷载会出现大于设计荷载的情况。需要说明的是，此处的台风极值风剖面是所有模拟台风统计意义上的结果，单个台风的风速剖面具有“低空急流”特征，且超梯度高度随风场位置是不断变化的，建议结合所有台风的全过程模拟，才能准确刻画台风竖向剖面对结构的作用特征。

图5 台风不同重现期年极值风速竖向剖面Fig.5 Vertical profile of annual extreme wind speed in different return periods of typhoon

2 大跨桥梁颤振失效概率评估

2.1 极限状态方程

桥梁结构颤振失效条件通常为桥址处的环境风速（检验风速）达到或高于桥梁的颤振临界风速，由此可定义桥梁结构颤振失效的极限状态方程为

式中：Z为桥梁颤振失效极限状态方程；vcr为桥梁结构的颤振临界风速；Gu为阵风因子；vb为桥址处的环境极值风速。

vcr由风洞试验或数值模拟结合理论分析获取，但受信息不足或环境因素影响，计算vcr的输入参数存在不确定性，且vcr对某些输入参数的变化极其敏感，即桥梁结构vcr真实值无法准确估计，可将其考虑为随机变量。近年来，已有很多学者提出了与颤振分析相关的参数不确定性量化方法，从而估计vcr的概率密度分布［17-18］。基于线性自激力模型的动力学方程，需分别量化桥梁结构的自振频率、阻尼比和主梁断面颤振导数的不确定性，自振频率的不确定性采用随机有限元方法估计，分别假设结构材料的密度ρ和弹性模量E服从正态分布和对数正态分布，各构件的变异系数（coefficient of variation，CoV）见表1，同时定义同一构件单元i和j的参数满足以下空间相关函数：

式中：ci，j和Δij分别表示单元i和单元j之间的相关系数和距离；L为桥梁构件的总长度，包括主梁、桥塔和主缆3部分；k为衰减系数，如表1所示。

表1 大跨度桥梁结构质量和刚度参数的概率模型Tab.1 Probabilistic model of structural mass and stiffness parameters of long-span bridges

参数相关性最弱的两个单元可认为是位于构件两端的单元，即Δij=L时对应的数值，即ci，j=exp(-k)，而当Δij=0时，ci，j取最大值1，即单元i与单元i自身的相关系数为1。现代悬索桥主缆通常采用高强钢丝，主缆各单元的质量和刚度沿其展向几乎不变，考虑到材料分布的不完全均匀性和其他施工误差影响，取最小相关系数ci，j=0.9，此时k=0.1。悬索桥的加劲梁通常由工厂预制的梁段拼接而成，考虑到所有梁段的施工工法和预制工艺是一致的，但加劲梁是拼装施工的，同时成桥状态还受路面铺装、附属设施和交通状况的影响，单元之间的最小相关系数应小于主缆，假设为ci，j=0.6，此时k=0.5。桥塔通常采用预应力混凝土现场浇筑，假定单元之间的最小相关系数为ci，j=0.5，对应的k=0.7。桥梁结构的阻尼比可基于大量的实测结果开展统计分析，分别假设一阶竖弯模态和扭转模态服从韦伯分布。伶仃洋航道桥闭口箱梁断面的颤振导数由风洞试验获取，通过重复30次节段模型自由振动试验，量化颤振导数由试验和识别算法造成的不确定性。由此分别采用二维三自由度分步分析（SBSA）和多模态分析（multi-mode）方法，计算得到的颤振临界风速vcr概率分布如图6所示，分步分析和多模态方法得到的均值、标准差分别为96.0、5.5 m·s-1和99.0、5.3 m·s-1。

图6 颤振临界风速概率密度分布Fig.6 Probability density distribution of flutter critical wind speed

阵风因子Gu主要用于考虑不同时距对颤振发生的影响，其数值可直接基于理论模型获得［19］。而大量的实测数据表明，阵风因子存在较大离散性，这与要和脉动风速的非高斯特征有关。本文基于Li等［20］关于台风实测数据的非高斯特性分析结果，采用阵风因子的非高斯理论模型［21］，对桥面高度从长时距10 min转换到阵风时距τ=3s和τ=60 s的阵风因子分别开展Monte Carlo模拟，结果如图7所示。

图7 阵风因子概率密度分布Fig.7 Probability density distribution of gust factor

2.2 颤振失效概率

颤振失效的临界点即为式（13）小于0，则颤振失效概率定义为

颤振失效概率Pf还可换算为正态分布对应的可靠度指标β，即

式中：Φ为标准正态分布的概率密度函数。

为确定台风作用下伶仃洋航道桥的颤振失效概率，基于上述各参数的概率密度函数，采用逆变换采样法生成随机样本，每个工况样本量为108，而后根据公式（15）可以计算其颤振失效概率。需要说明的是阵风因子和平均风速具有统计相关性，基于既有的实测结果［21］，本文假设两者线性相关系数为-0.5。

失效概率计算结果见表2。从表2可以看出，地表粗糙长度和阵风时距直接影响失效概率结果，任意100年失效概率最大的是z0=0.0002m、τ=3s时的8.4×10-3；本算例中由分步分析法得到颤振临界风速对应的失效概率略高于多模态方法；若只考了垂直于桥轴向的极值风速，失效概率将显著降低。

为判断伶仃洋航道桥在台风作用下的颤振安全性，表3给出了ASCE/SEI 7―16［7］建议的除地震、海啸和极端事件外荷载条件下的目标年失效概率Pf和50年可靠度指标β。由于大跨桥梁一旦发生颤振，就会产生大振幅振动并有可能导致结构倒塌，造成巨大的经济损失甚至是人员伤亡，此处将桥梁颤振失效归类为突发性的且会造成广泛连续破坏的结构失效，风险类别为IV，对应的目标年失效概率为Pf=1.0×10-7、50年可靠度指标为β=4.5。考虑到阵风时距τ=3s的阵风风速持续时间太短，不足以激励桥梁结构发生颤振，因此选表2中τ≥60s的结果进行比较。由表2可以看出，z0=0.01m对应的颤振年失效概率皆低于目标值，50年可靠度指标皆大于4.5；z0=0.0002m时，工况1和3的年失效概率大于1.0×10-7，但其未考虑风向的影响，相比之下，工况2和4只考虑了垂直桥轴向的极值风速，其年失效概率和可靠度指标皆满足目标值要求。由此可以认为深中通道伶仃洋航道桥在台风作用下颤振可靠度指标满足要求，具有足够安全保证。

表2 颤振失效概率Tab.2 Failure probability of flutter

表3 除地震、海啸和极端事件外的荷载条件对应的目标可靠度［7］Tab.3 Target reliability for load conditions except earthquakes,tsunamis and extreme events

3 结论

本文着眼于台风对桥梁的风致灾害，在缺乏大量实测数据的情况下，采用随机模拟的方法，通过构建三维台风风场模型和随机路径模拟方法，获取大量的台风风速样本数据，建立不同重现期目标的极值风速灾害曲线，为沿海大跨桥梁抗台风设计提供基础数据支持，并可直接扩展到基于性能的抗台风设计范畴，对推进我国建筑结构抗风理论体系从传统强风良态风向台风特异风的跨越具有重要意义。

以深中通道伶仃洋航道桥初步设计闭口箱梁方案为例，计算了桥址处不同重现期、不同高度的台风年极值风速，并考虑颤振计算的参数不确定性，采用二维分步分析和三维多模态分析方法分别计算了其颤振临界风速概率密度分布模型，由此开展了台风作用下大跨桥梁颤振失效概率评价，结果表明，伶仃洋航道桥满足规范的目标可靠度要求。

需要说明的是，实际的台风过程存在大风攻角、高湍流度等典型风场特征，本文的颤振分析仅考虑了均匀流场0°风攻角的情况，而大风攻角和高湍流度不仅会降低颤振临界风速，而且会进一步增大气动参数的离散性，相应颤振临界风速的离散性也会增大，有必要开展真实台风风场条件下桥梁结构的颤振风险评估。事实上，为了进一步提升颤振临界风速，伶仃洋航道桥最终方案采用了1.2 m上中央稳定板、95%高透风率检修道栏杆和检修轨道移至1/10处的综合气动控制措施，具有足够的颤振安全冗余度。

作者贡献声明：

方根深：台风模拟，数据处理，论文撰写与修改。

赵 林：学术指导与论文修改。

卫苗苗：数据整理，论文撰写与修改。

李 珂：学术指导与论文修改。

葛耀君：学术指导与论文修改。