考虑微裂纹演化时间效应的混凝土动力损伤本构模型

海 鲁，李 杰

（同济大学土木工程学院，上海 200092）

自1917年Abrams［1］首次发现混凝土的应变率效应，人们对混凝土动力力学特性的研究已有一百多年的历史。大量试验数据表明，混凝土在动力作用下强度表现出率敏感性，即抗拉强度和抗压强度随着应变率的增加而提高［2-3］。原因一般归结为材料本身的黏性特性、微细观裂纹演化效应和宏观惯性作用3种物理机制［4-6］。相比黏性特性，在爆炸、冲击等中高应变率作用下，微裂纹演化效应和宏观惯性作用对材料动力性能的影响更为显著。通常认为：在动力分析时宏观惯性作用可自动得到反映，微裂纹演化效应则需在本构模型中加以考量［7］。

自Ladevèze［8］和Mazars［9-10］在混凝土损伤力学理论研究中做出开创性工作后，损伤本构模型逐渐成为混凝土结构非线性分析的有效工具。李杰等［11］、Wu等［12］建立的双标量弹塑性损伤模型，能够全面反映混凝土的非线性力学行为，且数值算法相对简单。文献［13-15］从随机性与非线性耦合的角度建立损伤萌生与随机演化的基本法则，系统发展了细观随机断裂模型，实现了混凝土力学性质随机性与非线性的综合反映。在损伤力学的框架下，为反映混凝土的率敏感性，一些研究者考虑应变率效应的物理机制建立动力损伤模型［16-17］。

但现有研究大多仅通过黏性规则化等方式考虑材料的黏性效应及其对损伤演化的影响，而对微裂纹尖端的惯性和其他耗散机制所导致的演化率敏感性和时间效应，并没有充分考量。而后者的合理量化对于中、高应变率作用下的混凝土材料本构建模十分关键。基于此，本文提出了有效损伤驱动力的概念，引入微惯性和微黏性，结合细观随机断裂模型，给出动力损伤演化法则，在宏观层次量化了微细观层次裂纹扩展的率相关性，从而建立了一类适用于强动力作用下混凝土非线性分析的损伤本构模型。

1 混凝土双标量弹塑性损伤理论

应变张量ε可分解为弹性应变张量εe和塑性应变张量εp两部分，即

根据应变等效假定，有效应力定义为［18］

式中：E0为初始弹性刚度。

为反映混凝土的拉压各向异性，对有效应力张量引入如下所示的正负分解［11］：

式（3）～（5）中：正负投影张量P+和P-分别定义为

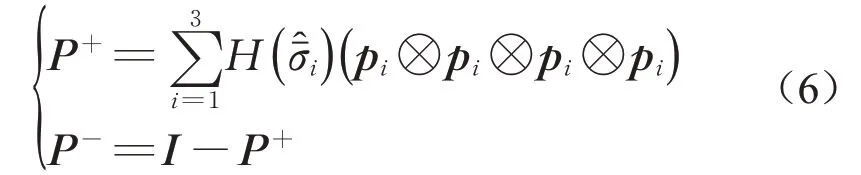
基于等温绝热条件下材料的弹性Helmholtz自由能势和塑性Helmholtz自由能势不耦合的假定，材料的总弹塑性Helmholtz自由能势可以表述为［18］

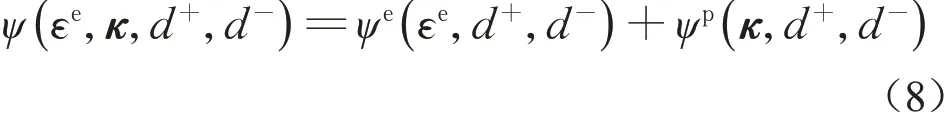
式中：ψe与ψp分别为材料的弹性和塑性Helmholtz自由能；d+与d-分别为受拉和受剪损伤变量；κ为塑性硬化内变量。

对于弹性Helmholtz自由能，基于上述有效应力的正负分解和损伤变量的引入，可以分解为［18］

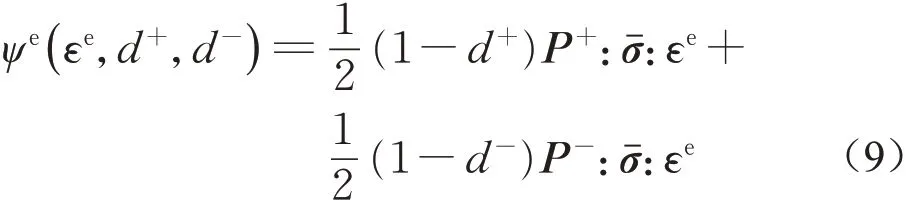
类似地，塑性Helmholtz自由能可以表达为［18］

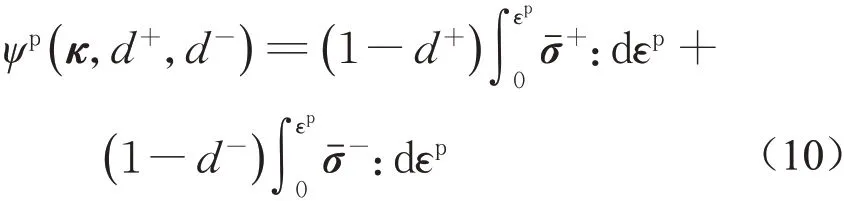
材料的损伤和塑性演化过程都是不可逆的热力学过程，其能量耗散均应为非负值，本构方程必须满足以下Clausius-Duhem不等式：

将式（8）微分并代入式（11），可得到

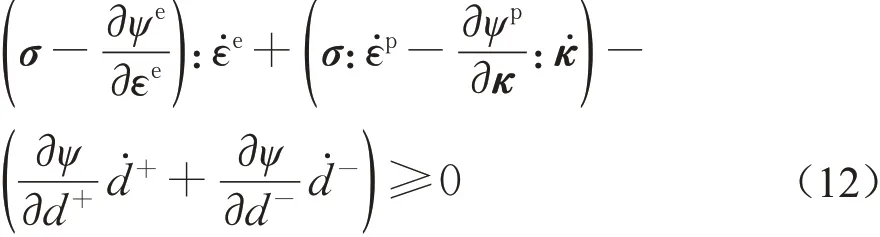
考虑ε̇e的任意性，要满足上述不等式要求，可得

考虑式（13），将式（9）所定义的弹性Helmholtz自由能代入，可得

式中：四阶损伤张量D表示为

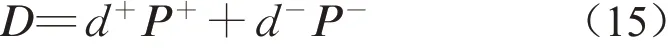
式（14）即为混凝土双标量弹塑性损伤本构模型。

2 损伤和塑性演化准则

2.1 有效损伤驱动力

根据Clausius-Duhem不等式（11），可得到如下损伤耗散不等式

式中：Y+与Y-分别定义为受拉和受剪损伤能释放率。

由式（16）和（17）可知，选取损伤能释放率作为损伤驱动力，所得结果必然不违背热力学第二定律，因此，损伤演化准则在一般意义上可以表示为

当忽略塑性变形对材料受拉Helmholtz自由能的影响，选择Drucker-Prager作为塑性势函数，经过推导和简化［11，18］，可以得到受拉和受剪损伤能释放率的表达式分别为

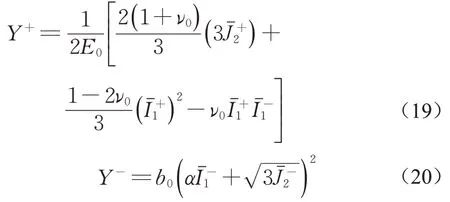
式（19）、（20）中：E0与ν0分别为材料的初始弹性模量和泊松比；分别为对应有效应力的第一不变量；分别为对应有效应力偏量的第二不变量；b0与α定义为材料常数。

事实上，在中、高应变率作用下，由于在微细观尺度裂纹尖端存在惯性和其他耗能机制，则相比准静态过程，微裂纹扩展的驱动力会有所滞后，正是这种驱动力的滞后效应使得微裂纹扩展表现出率敏感性和时间相关性，从而宏观层次材料特性表现应变率效应。而损伤是对微裂纹演化的宏观描述，损伤驱动力即损伤能释放率会有相应地滞后，为在宏观层次表征这一物理过程，引入如下方程：

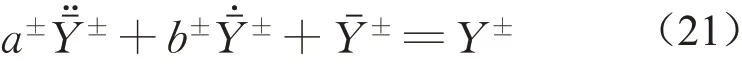
式中：分别定义为有效受拉和受剪损伤能释放率，即有效损伤驱动力，由于有效损伤能释放率对时间的二阶导数和一阶导数的引入，损伤驱动力的滞后效应得以表征；a±分别对应受拉和受剪的微惯性系数；b±分别对应受拉和受剪的微黏性系数。相应地，损伤演化法则表示为

2.2 损伤演化方程

为确定损伤演化法则，本文引入细观随机断裂模型［13-15］。如图1所示，结构代表性体积元离散为一系列相互并联的微弹簧，并假定弹簧两端与刚性板连接。在这一模型中，各微弹簧的性质代表材料的微观特性，而弹簧系统的集合性质表征了代表性体积元的性质。

图1 细观随机断裂模型Fig.1 Mesoscopic stochastic fracture model

假定微弹簧的应力-应变关系为理想弹脆性，如图2所示，且各个微弹簧的断裂应变为随机变量。在加载过程中，微弹簧的渐进断裂导致了整体系统的力学行为偏离线性，呈现出非线性和软化的特征。因此，宏观代表性体积单元的损伤变量可定义为［13-15］

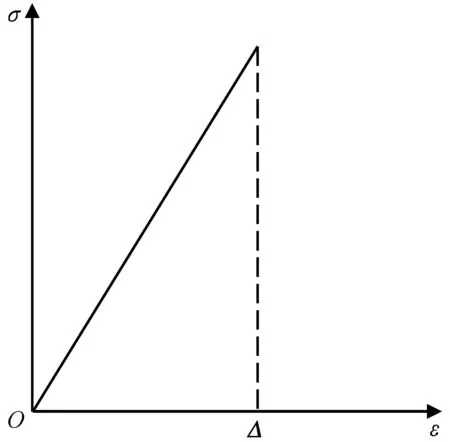
图2 弹簧应力应变关系Fig.2 Stress-strain relation for micro-springs

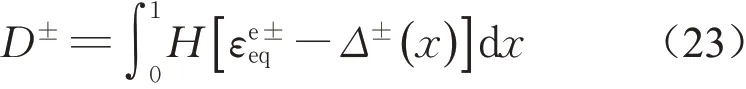
式中：Δ±(x)分别为受拉和受剪断裂应变随机场；分别定义为受拉和受剪能量等效应变，表达式分别为

由于断裂应变为随机变量，图1所示的随机系统不仅可以很好地反映混凝土力学性质的非线性，也可以综合反映混凝土应力-应变关系的随机性。即细观随机断裂模型实现了混凝土受力力学性质随机性与非线性的综合反映。对损伤演化方程式（23）两边分别求数学期望，得到损伤的均值演化规律为

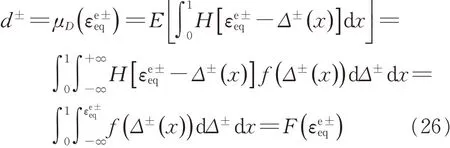
式中：f(·)和F(·)分别为断裂应变随机变量的一维概率密度函数和累计分布函数。

试验研究证实，受拉和受剪断裂应变随机场的一维概率分布一般为对数正态分布［18-19］，其均值和标准差分别为μΔ±和σΔ±。令

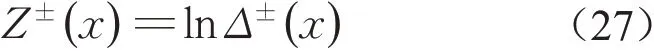
满足正态分布，其均值和标准差分别为

因此，Δ±(x)的一维概率分布函数为

式中：Φ(·)表示标准正态分布的累计分布函数。

2.3 塑性演化

塑性应变对混凝土本构关系的建模有不可忽略的影响。为简单起见，本文采用如下简化形式的塑性应变演化控制方程［19］：

式中：与为控制塑性演化的材料参数。

并认为塑性应变也可以基于有效应力张量分解的思想分解为正负两部分，即

3 算例及验证

本文所提出的模型涉及的材料参数如表1所示。其中，弹性参数、损伤演化参数和塑性参数的取值参照文献［19-20］。而本研究所提出的动力损伤参数的取值由单轴受拉强度和受压强度的动力提高曲线拟合得到。需要指出，在此忽略了混凝土强度等级、骨料种类等因素对动力损伤参数取值的影响，更为精确的参数取值方法将做进一步研究。

表1 动力损伤本构模型参数Tab.1 Parameters of dynamic damage constitutive model

此外，为聚焦本文研究目标，以下分析实例均只涉及确定性分析内容，而对混凝土动力效应的随机性影响另文专门论述。

3.1 应力-应变曲线

首先对混凝土单轴受拉应力-应变全曲线进行数值模拟。通过控制加载速率实现3种应变率，分别为0.001s-1、10 s-1和20 s-1。模拟中所采用的材料参数分别为：E=34700MPa，λ+=4.7536，ζ+=0.656，a+=3.0×10-10s-2，b+=3.0×10-5s-1，=0.6，=0.1。

模拟所得到的3种应变率下混凝土受拉应力应变全曲线如图3所示。从图3可以看出，随着应变率的提高，混凝土单轴受拉峰值应力及对应应变逐渐增加，从而验证了本文所提出的模型能够较好地反映混凝土在中、高应变率作用下的强度明显提高等动力力学行为。

图3 单轴受拉全曲线Fig.3 Uniaxial tensile curves

3.2 动力强度提高因子

混凝土在动力作用下的率相关效应可用动力强度提高因子（即动力强度与静力强度之比）来描述。采用本文模型，通过数值模拟分别计算了单轴受拉和单轴受压条件下不同应变率对应的动力强度提高因子，所得到的结果与经典试验结果［21-31］对比如图4、5所示。模拟中，关于受拉的材料参数同3.1保持一致，关于受压的材料参数取值分别为：λ-=7.471，ζ-=0.3767，a-=5.0×10-12s-2，b-=2.0×10-6s-1=0.4，=0.1。通过对比可发现，本文所提出的模型基本能够反映强度随应变率的变化趋势，尤其是能够描述在中、高应变率范围内强度的大幅度提高。

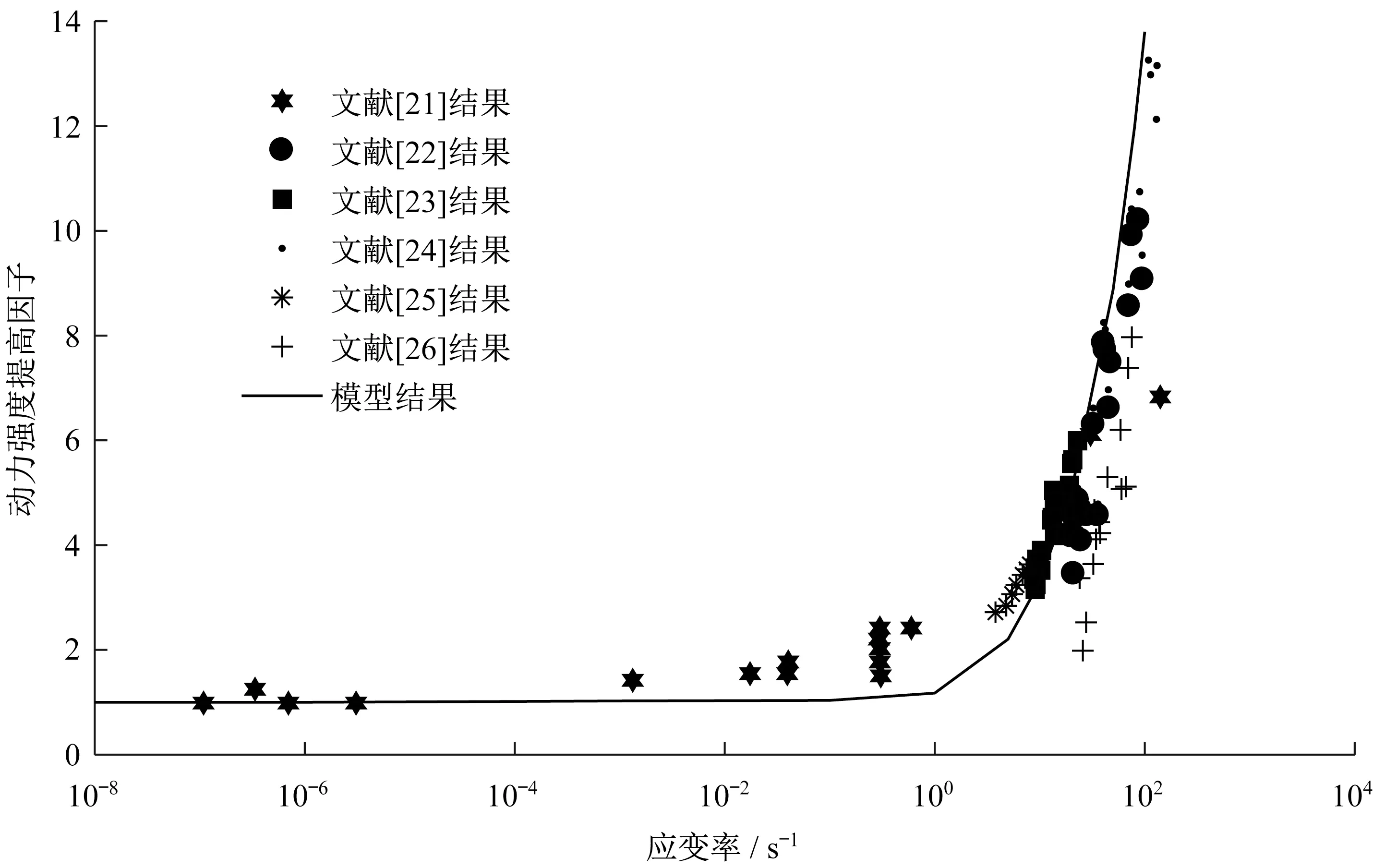
图4 受拉动力强度提高因子Fig.4 Dynamic increase factors under tension

3.3 混凝土层裂试验

Hopkinson杆层裂试验是探究混凝土在冲击、爆炸等强动力作用下动态拉伸强度的重要技术。为进一步验证所提出模型的有效性，本文选择Schuler等［32］所作的混凝土层裂试验，采用三维有限元模型进行了数值模拟。

图5 受压动力强度提高因子Fig.5 Dynamic increase factors under compression

Schuler等人的试验装置见图6，由直径同为75 mm，长度分别为60、5 500、250 mm的撞击器、入射杆和混凝土试件组成。试验中，通过撞击器撞击入射杆产生压缩波，压缩波传入混凝土试件并在试件自由端发生反射形成拉伸波，在拉伸波的作用下混凝土发生动态断裂，而通过控制撞击器的速度，可测试试件在不同应变率下的力学行为。

图6 层裂试验装置（单位：毫米）Fig.6 Setup of spall test(unit:mm)

本文选取4.1、7.6和14.1m·s-13种冲击速度，将撞击器、入射杆和混凝土试件综合建模，并进行数值分析。分析中，混凝土采用本文所提出的动力损伤本构模型，材料参数取值为：E=38900MPa，λ+=5.43，ζ+=0.54，a+=1.0×10-10s-2，b+=3.0×10-5s-1，ξ+p=0.6，n+p=0.1，λ-=8.43，ζ-=0.42，a-=6.5×10-12s-2，b-=2.5×10-6s-1，=0.4，=0.1。

在Hopkinson杆试验中，试件自由端的pull-back速度（即自由端质点速度从峰值到最低点的差值）是衡量混凝土动态抗拉强度的重要指标。本文数值模拟所得到的3种冲击速度下混凝土自由端的速度时程曲线如图7所示。由此所计算得到的pull-back速度和试验结果见表2。通过数值结果和试验结果对比可知，本文所提出的模型用于结构分析时能够较好反映混凝土在强动力作用下的力学行为。

表2 试验和数值结果的对比Tab.2 Comparisons of test and numerical results

图7 试件自由端速度时程Fig.7 Speed of free end of specimen

4 结论

在混凝土弹塑性损伤理论的基础上，提出了有效损伤驱动力的概念，引入微惯性和微黏性量化由于细微观层次裂纹演化时间效应而导致的宏观层次损伤滞后的效应，从而可以反映混凝土在爆炸、冲击等强动力荷载作用下的应变率效应。通过数值模拟结果的分析与对比，本文所提出的模型能够较好地描述混凝土在中、高应变率作用下的力学行为，可以应用于混凝土结构在强动力作用下的非线性分析。

作者贡献声明：

海 鲁：提出模型，进行数值模拟和撰写论文。

李 杰：提出研究方向，审阅、修改论文。