面齿轮参数对供弹传动系统影响分析

李毅恒,李 强,陈 赟,叶军雄,曹广群

(1.中北大学 机电工程学院，太原 030051；2.中国南方工业研究院，北京 100000；3.西北机电工程研究所，陕西 咸阳 712000)

1 引言

随着现代小口径防空火炮射速的不断提升，供弹系统的稳定传动对整个自动机系统的可靠性有着关键作用。为了进一步提高火炮射速和其工作稳定性，无链供弹技术应运而生，是现代高射速小口径火炮供弹系统的重点研究方向[1]。供弹系统高速供弹时，供弹机构相互冲击、碰撞完成规定动作。供弹构件的设计加工误差，会导致供弹传动过程的不平稳，出现停射、卡弹等现象，是影响火炮射速的关键因素之一。因此，本文在转鼓式无链供弹系统中，重点以集弹盘面齿轮供弹机构为研究对象，设计了一种基于精确点建模的集弹盘面齿轮,并对不同模数、不同压力角的集弹盘面齿轮对传动系统振动特性的影响进行了分析。

面齿轮传动是一种圆柱齿轮与面齿轮相互啮合的传动形式，国外研究者对此研究较早并应用于军事等领域[2]。如面齿轮传动技术应用到直升机传动系统中，可明显提高动力分流效果，减轻传动系统重量，并且增强了承载能力。具有面齿轮传动的主减速器结构装配在美国阿帕奇直升机中，使其质量减轻22%，传动性能提高35%[3]。面齿轮传动有很多优点，承载能力好、重量轻、噪音小、传动重合度大、动力分流效果好、振动小[4]。

在闵杰的研究中，分析了拨弹轮齿数对供弹系统运动的影响，证明了拨弹轮齿数对炮弹在不同单元交接有直接影响[5]。在刘志桐的研究中，说明了无链供弹提弹机构与弹间隙对炮弹在不同单元之间的交接有直接影响，不同间隙会导致弹在交接过程中出现卡弹情况[6]。在Litvin等的研究中，对面齿轮最大外径、最小内径等基本参数和刀具齿数的关系进行了研究分析[7]；在朱如鹏的文献中对面齿轮建模进行了研究，在 Matlab 中得到单齿齿面图形，再导入三维建模软件进行建模[8]；王尧等研究者，对X(径向放样法)和Z(齿根齿顶放样法)2种面齿轮截面法建模方法进行了比较，说明了Z截面放样法可以更好地完成各种参数的正交直齿面齿轮建模[9]。

本文以某供弹系统的供弹构件集弹盘面齿轮为研究对象，为了增加面齿轮传动仿真的真实性，先对其进行参数化精确点建模。并对不同模数、不同压力角的集弹盘面齿轮对传动系统振动特性的影响进行了分析。为提高武器射速、提升供弹系统传动稳定性有一定借鉴意义。

2 无链供弹系统结构及运动原理

2.1 无链供弹系统结构

高射速转管武器的供弹系统主要分为有链供弹和无链供弹两大类。有链供弹是通过弹链将弹丸固定并与自动机进弹组件连接，通过自动机进弹时的拨弹轮将弹丸拨出进行供弹。无链供弹主要通过弹鼓或弹箱进行补弹，通过相关的软导引、与自动机进弹接口相连接，实现快速供弹。本文采用弹鼓式无链供弹系统，结构如图1所示。其中，集弹盘面齿轮是重要的动力传动装置，集弹盘面齿轮设计参数是否合理直接影响供弹传动能否平稳。

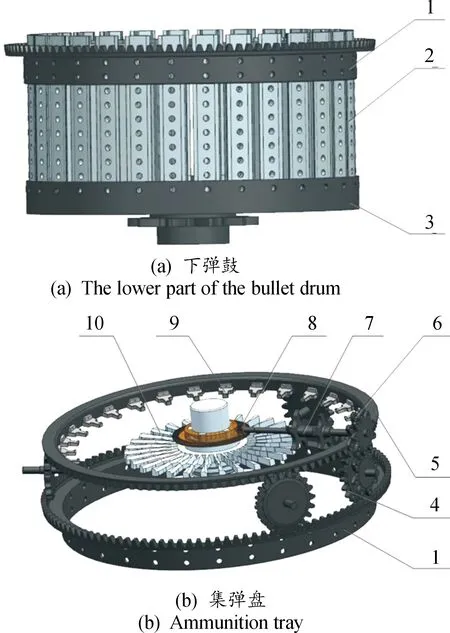
1-中间传动面齿轮；2-弹尾卡槽；3-底部大齿轮；4-周向齿轮；5-集弹盘面齿轮；6-大模数齿轮；7-弹鼓出口拨弹轮；8-锥齿轮1、2；9-集弹盘弹尾导引；10-集弹盘前卡槽

2.2 无链供弹系统运动原理

本文所设计的无链供弹系统在弹鼓中间安有螺旋片，弹丸在螺旋运动进弹过程中以螺旋片为前支点；弹丸弹尾卡在根据弹尾凸缘设计的弹尾导槽中。系统正常供弹时，螺旋片固定不动，弹尾卡槽在齿轮带动下带动弹丸运动，弹丸由前支点螺旋片和后支点弹尾卡槽双重约束。进弹时，弹丸螺旋上升至出口处，由拨弹轮及铲弹导引片将弹丸送入集弹盘内，再由集弹盘前后约束下将其送入弹鼓出弹口。

图2 集弹盘整体模型图

集弹盘面齿轮接收从下弹鼓传送到的弹丸，并使弹尾约束在集弹盘弹尾卡槽，弹头约束在集弹盘前卡槽内，使弹丸继续跟随集弹盘转动向自动机供弹。集弹盘面齿轮与集弹盘弹尾卡槽相互固定，而且集弹盘面齿轮通过3个周向齿轮与中间传动面齿轮进行动力传动，带动整个集弹盘及集弹盘上的弹丸转动。集弹盘面齿轮是重要的动力传动机构，集弹盘面齿轮设计合理与否将直接影响能否顺畅供弹传动和射速提升。因此，选择对集弹盘面齿轮进行重点研究，结合面齿轮精确点建模技术构造集弹盘面齿轮三维模型，并选取不同模数、不同压力角的面齿轮进行动力仿真，进而研究集弹盘面齿轮传动过程中的振动情况。

3 集弹盘面齿轮建模

关于面齿轮精确点建模有多种方式，王尧[9]根据面齿轮的齿面及过渡方程，推导了正交直齿面齿轮垂直于X轴和垂直于Z轴的截面方程，基于CATIA软件建立了正交直齿面齿轮模型，经比较得采用Z截面放样法建模更优；南耀仕[10]采用Z向截面放样法在Matlab中求解得到了面齿轮齿面方程和过渡齿面方程的解，并实现齿面离散点和齿面轮廓的可视化，将齿面离散点数据导入UG，最终在UG中建立了面齿轮的三维模型。笔者综合借鉴了王尧[9]的Z截面放样法与南耀仕[10]的方法运用Matlab进行齿面方程计算，在UG中对面齿轮进行建模。具体流程如图3所示。

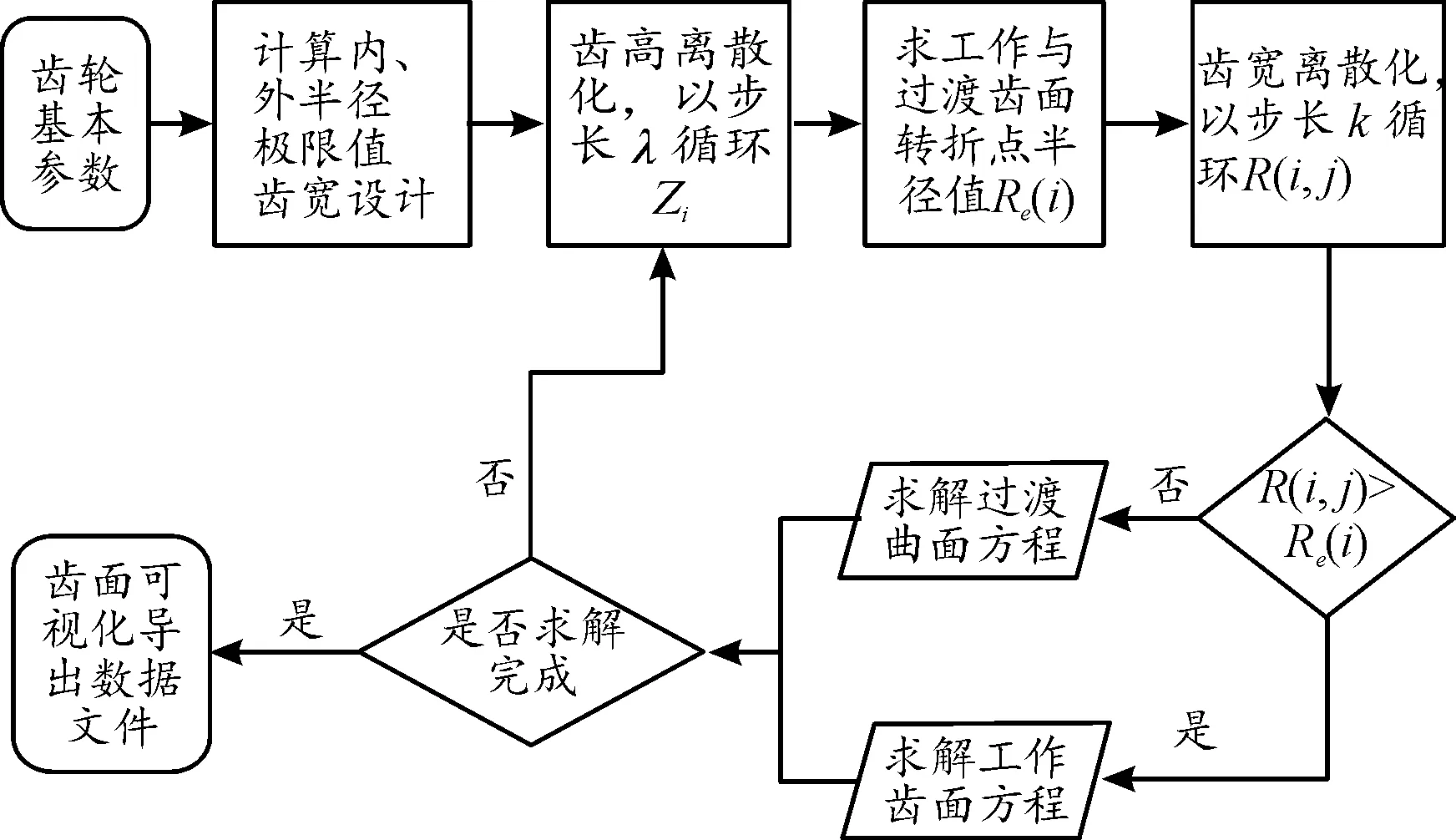
图3 面齿轮齿面点计算流程框图

3.1 齿面方程和刀具齿面方程的建立

面齿轮的加工坐标系由2个静坐标系S1(O1,X1,Y1,Z1),S2(O2,X2,Y2,Z2)和2个动坐标系Sh(Oh,Xh,Yh,Zh),Sp(Op,Xp,Yp,Zp)组成。S1和S2代表着刀具的固定坐标系和面齿轮的固定坐标系。Sh和Sp代表着刀具的动坐标系和面齿轮的动坐标系。初始位置时，刀具的静坐标系和动坐标系S1、Sh重合，面齿轮的静坐标系和动坐标系S2、Sp重合。图4表示面齿轮加工坐标系。Z1轴表示刀具做加工运动时的轴线，Z2轴表示面齿轮做加工运动的轴线。

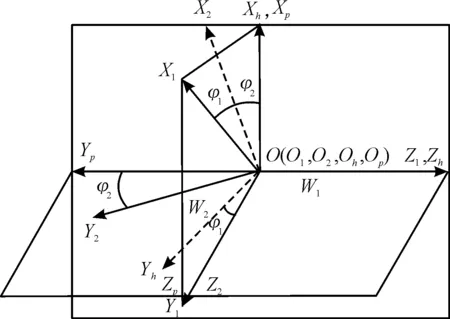
图4 面齿轮加工坐标系

图5表示刀具齿面渐开线参数，其坐标系与图4所示坐标系相对应。

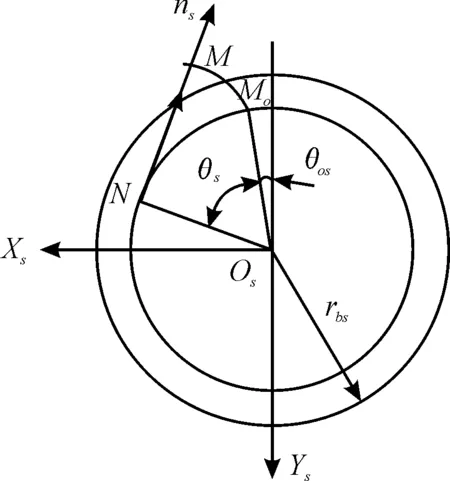
图5 刀具渐开线齿面的参数示意图

刀具的齿面轮廓图形在刀具动坐标系下，刀具渐开线齿面方程为：

(1)

由转换矩阵可知面齿轮工作齿面点坐标为：

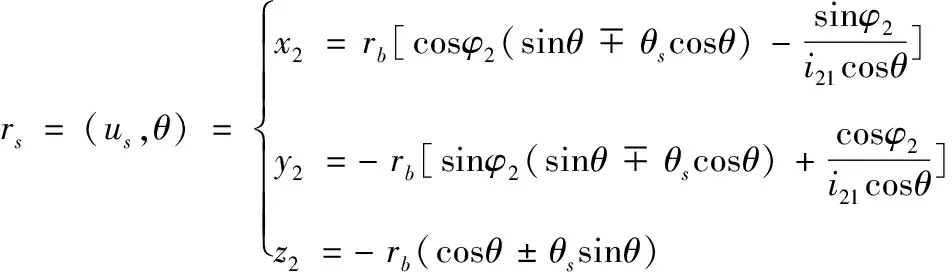
(6)

式中θ=θs+θos+φ1，φ2=i21·φ1

过渡齿面是由刀具齿顶加工而成的，可得面齿轮过渡曲面方程：

(7)

式中:

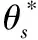
(8)

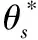
根据根切条件，可以得到面齿轮的最小内半径为：

(9)

根据齿顶变尖条件，可以得到面齿轮的最大外半径值为:

(10)

可以依据最大外半径和最小内半径设计出面齿轮齿宽。

3.2 面齿轮齿面点求解

根据面齿轮齿形特性，可采用2种放样方法对面齿轮轮齿进行截面放样：Z向截面放样法(齿根齿顶放样法)和X向截面放样法(径向放样)法。本文采用Z向截面放样法求取过渡曲面方程。

正交直齿面齿轮的齿轮模型如图6所示。截面关于坐标平面YOZ面对称。截面齿廓由过渡曲面截线DE和齿面截线EF组成，两侧截面连接线都是以面齿轮转轴为圆心的圆弧。齿面中部弧线为面齿轮过渡曲线，上部分为面齿轮工作齿面，下部为面齿轮过渡齿面。

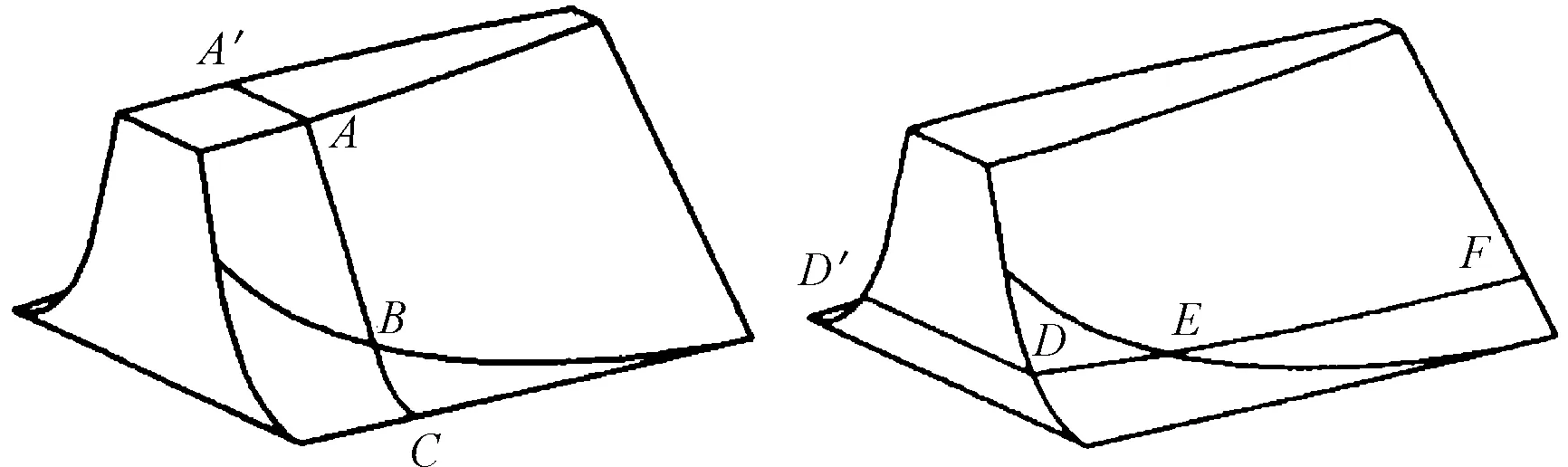
图6 正交直齿面齿轮模型示意图

运用Matlab求出每一R(i, j)处的值，即可解得相应面齿轮的工作齿面和过渡曲面各点坐标[11]。

3.3 基于UG进行面齿轮建模

本文是根据插齿法齿轮加工原理，构建出面齿轮传动的运动模型。面齿轮毛坯和刀具按顺时针绕各自轴线转动，在相同时间内两者转过的角度比为齿数比，以确保加工出完整的齿面[13]。

建模方法是基于齿面数学方程的精确建模方法[12]。根据上文Matlab中求解出的齿面离散点，在UG中将各个点汇集成线，利用网格曲面集线成面的精确建模方法。具体流程如图7所示。

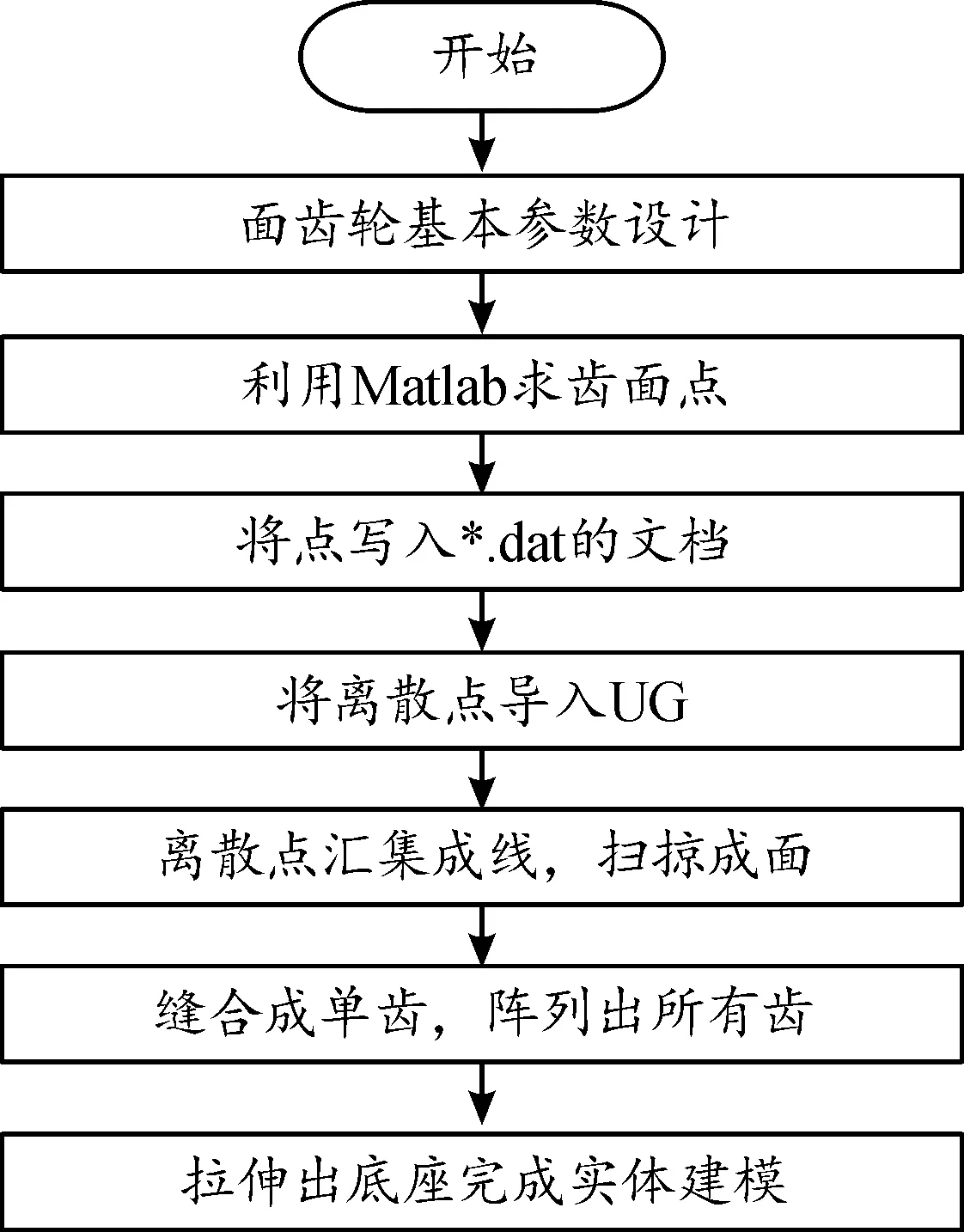
图7 面齿轮UG建模流程框图

完成面齿轮建模如图8所示。

图8 面齿轮在UG中建模流程示意图

完成了对集弹盘面齿轮的精确点建模。

4 集弹盘面齿传动系统动力学分析

4.1 仿真过程

将经过精确点建模的集弹盘面齿轮和与其相啮合的周向圆柱齿轮进行动力学仿真，并对其仿真结果进行分析。进行动力学仿真的前提条件如下：

1)将集弹盘面齿轮与周向圆柱齿轮传动作为主要研究对象，由于3个圆柱齿轮相同，重点研究一个周向圆柱齿轮与集弹盘面齿轮的啮合传动情况。

2)经过精确点建模后的面齿轮与真实面齿轮仍存在一定误差，进行运动学仿真时将此误差忽略。

3)由于仿真具有一定局限性，仿真结果只能证明笔者所用的方法理论在一定情况下可行。

集弹盘面齿轮传动模型如图9所示，将模型保存为x_t格式文件，导入ADAMS中。设置齿轮参数：模数取5，压力角为20°，面齿轮齿数106个，周向圆柱齿轮齿数取19,齿轮材料为钢(steel)。集弹盘面齿轮中心与地面之间设置旋转副，周向圆柱齿轮中心与地面添加旋转副，集弹盘面齿轮与周向圆柱齿轮之间设置为接触状态。

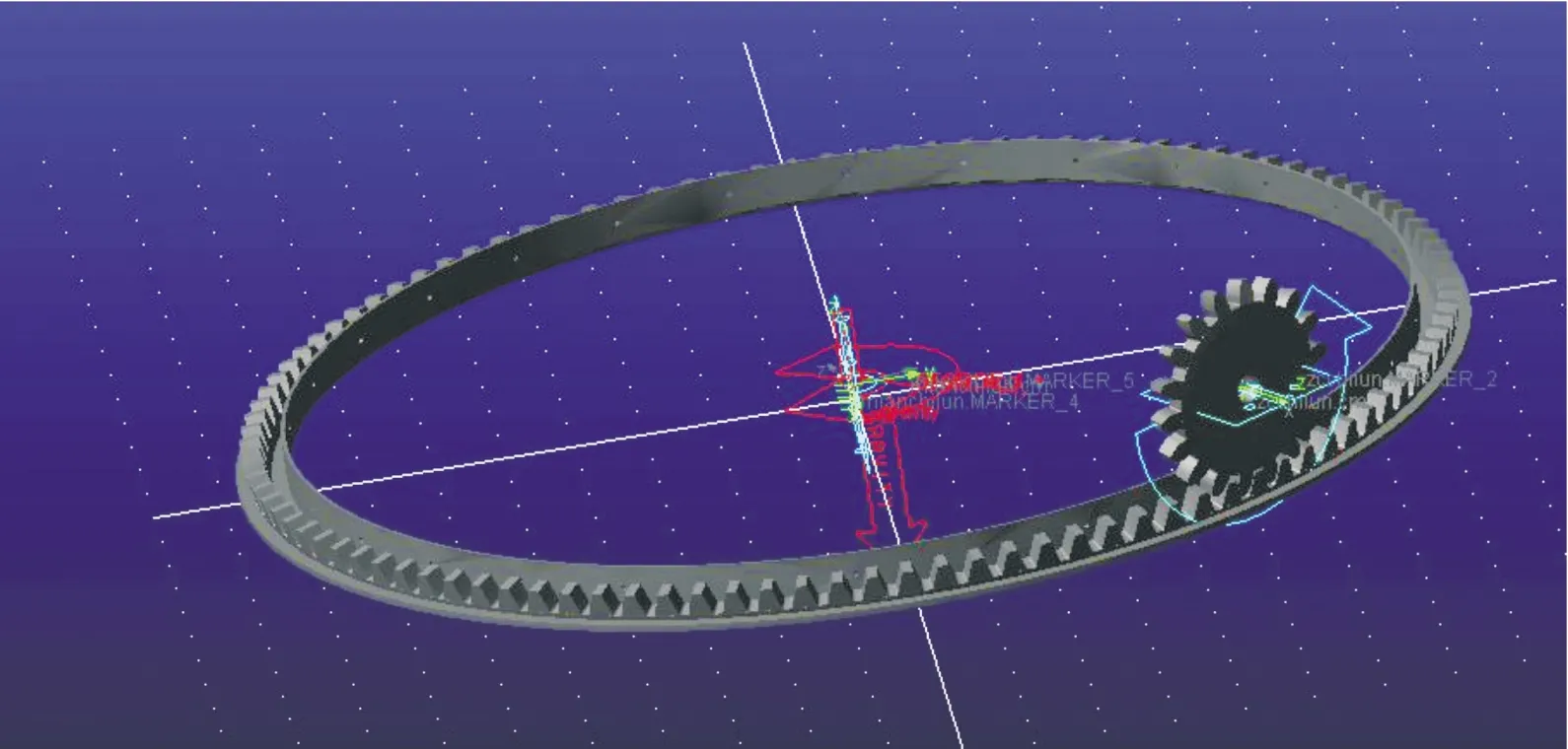
图9 ADAMS中的传动模型示意图

为模拟供弹时的机构运动情况，在周向圆柱齿轮旋转副上添加驱动，集弹盘面齿轮上添加负载扭矩，驱动转速为1 000 r/min，设置仿真时间5 s，仿真步长为500步。模型接触副中阻尼(damping)为10.0，动力系数(dynamic coefficient)0.1，材料刚度(Stiffiiess)为1.0×105N/m，材料刚度贡献值指数(Force Exponent)为2.2，静摩擦系数(static coefficient)为0.3[14]。

4.2 仿真结果分析

由图10可知由于在啮合过程中，集弹盘面齿轮与周向齿轮在传动过程中存在周期性冲击作用，故速度曲线呈现周期性波动趋势，集弹盘面齿轮与周向齿轮在啮合传动过程中存在周期性振动。

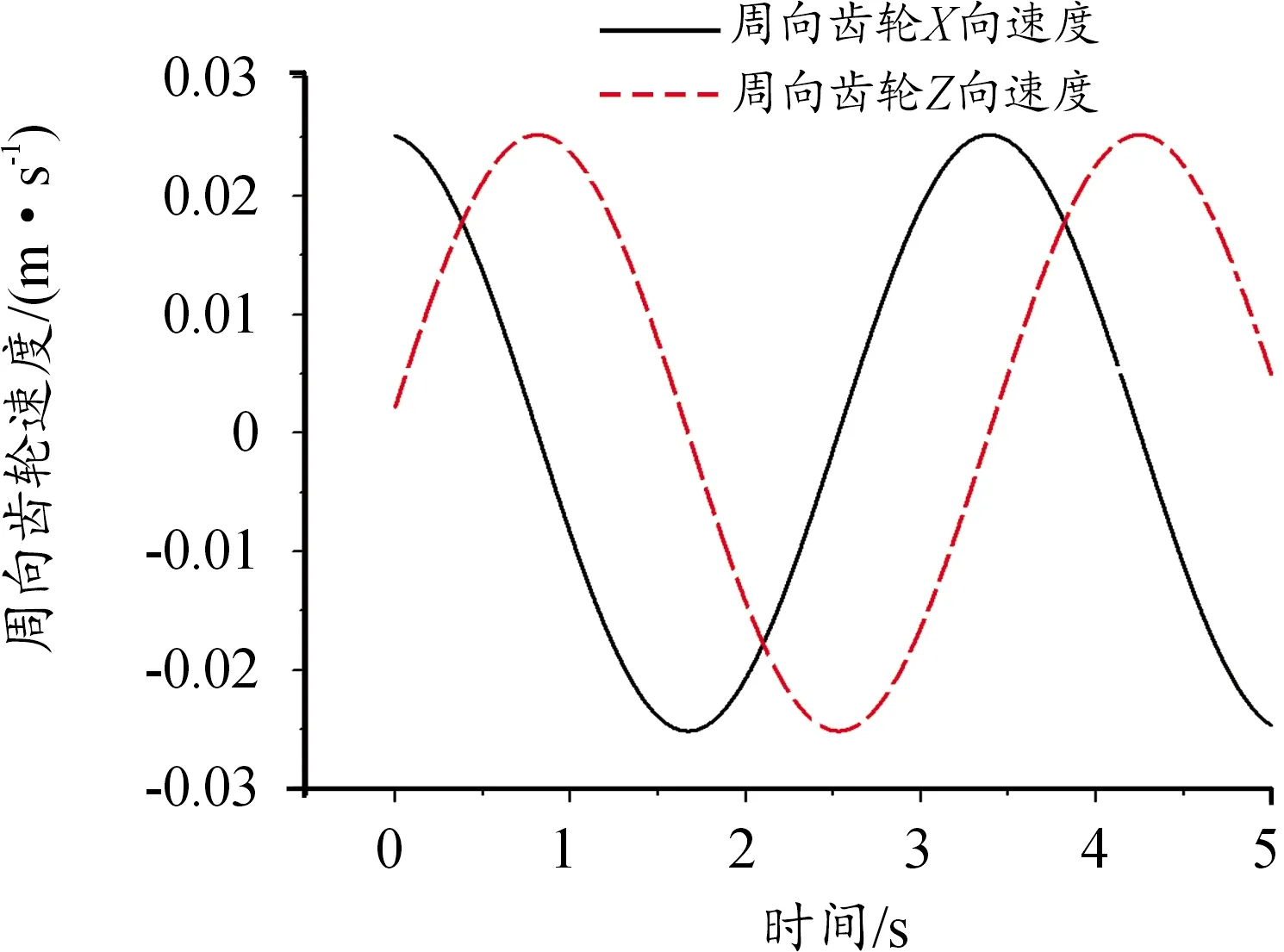
图10 周向齿轮X、Z方向速度曲线

集弹盘面齿轮在供弹过程中转速较高，故面齿轮传动系统振动属于高频振动问题，即振动位移及速度副值较小，而加速度却比较敏感，所以本文选择通过分析面齿轮的加速度来度量其振动量的大小[15]。仿真结果主要取面齿轮X、Y方向加速度进行振动分析。仿真结果如图11和图12所示。

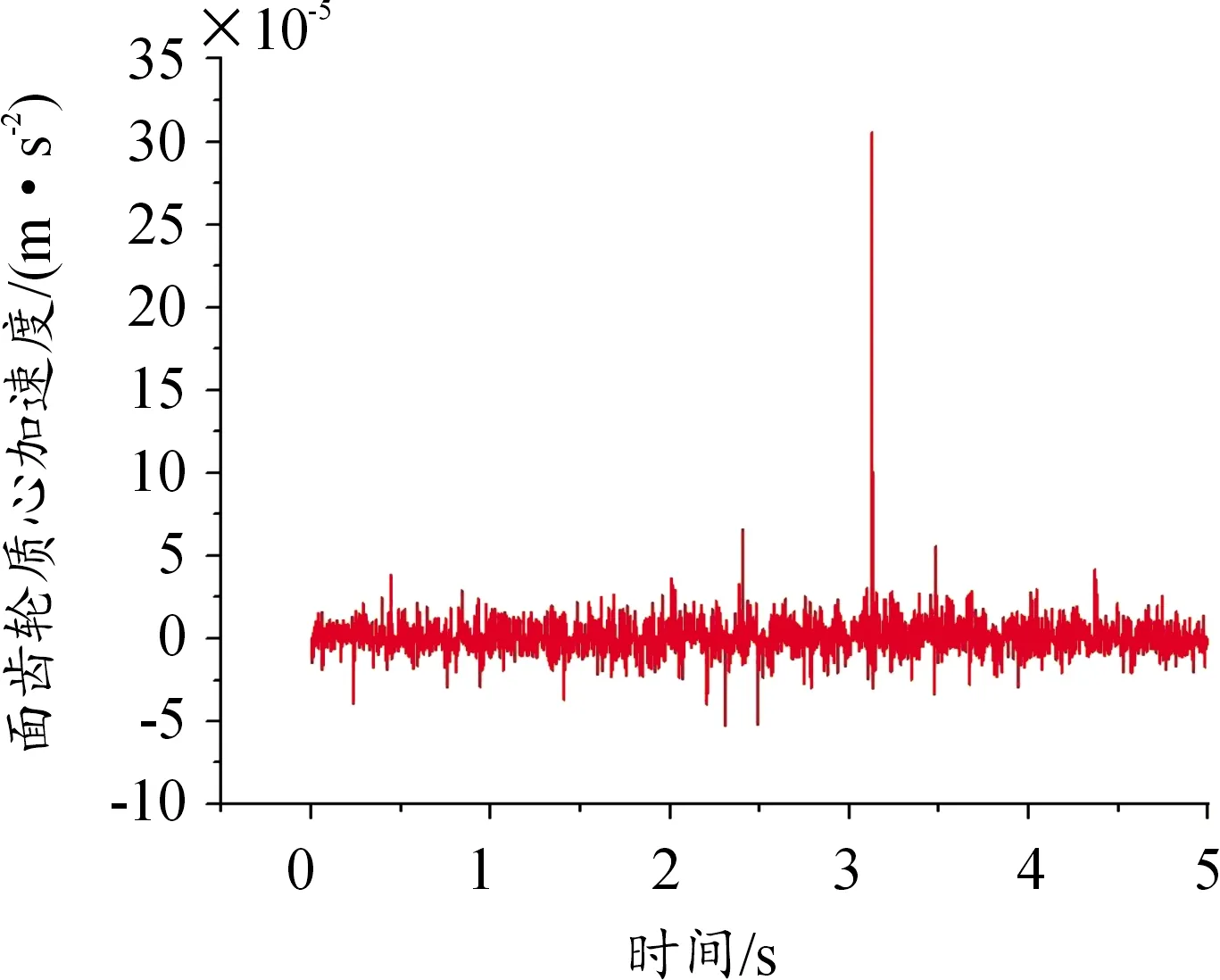
图11 面齿轮质心X方向加速度曲线

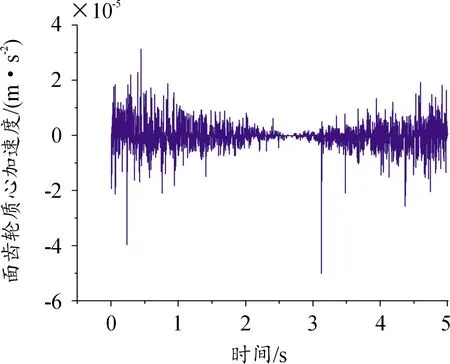
图12 面齿轮质心Y方向加速度曲线

为研究集弹盘面齿轮与周向齿轮在传动过程中的振动情况，重点分析了面齿轮质心X、Y方向的加速度由图可见面齿轮X方向加速度以0为中心值上下波动，在某些时刻存在峰值较大的情况；面齿轮方向加速度呈现由大到小再到大的趋势，中间有一阶段加速度值小且平稳。

模数是对齿轮制造的各方面性质都有重要影响。一般齿轮模数越大，齿轮强度越高、刚性越好。在齿轮设计中选定齿轮模数是十分重要的[14]。为了分析模数对集弹盘面齿轮振动特性的影响，分别建立了模数为3、4、5、6的面齿轮组，其他条件均相同。

压力角对齿轮啮合性能有较大影响，一般压力角越大，吃面啮合点的正应力及剪应力都会变小，压力角对面齿轮振动的影响也十分重要[14]。为了分析压力角对集弹盘面齿轮振动特性的影响没，分别建立了压力角为20°、21°、22°、23°、24°的面齿轮组，其他条件均相同。

对集弹盘面齿轮不同模数和不同压力角的啮合传动仿真结果如表1、表2所示。

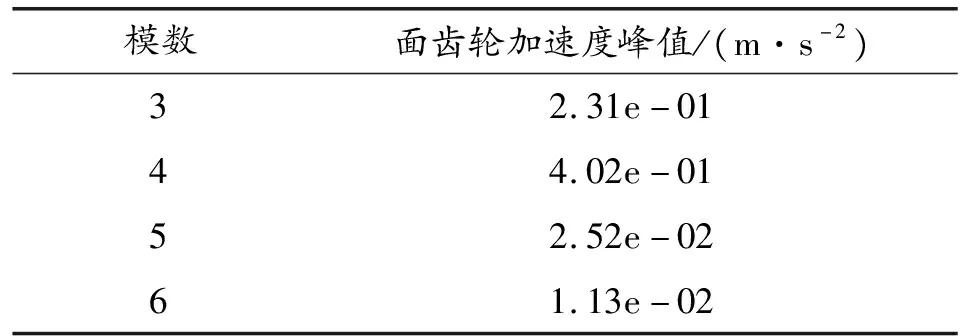
表1 不同模数时面齿轮加速度峰值

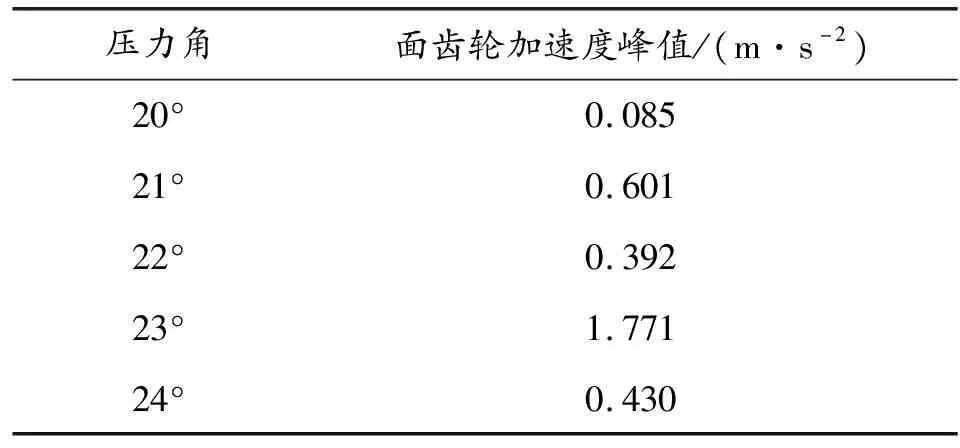
表2 不同压力角时面齿轮加速度峰值

5 结论

对某转管武器无链供弹系统的供弹构件集弹盘面齿轮进行参数化精确点建模，并对不同模数、不同压力角的集弹盘面齿轮对传动系统振动特性的影响进行了分析。结果表明：在仿真情况下，一定范围内集弹盘面齿轮模数越大，传动系统振动越小；压力角为23°时，传动系统振动最大。本文研究结果可以作为武器系统机构减振设计参考，对于提高武器射速、提升供弹系统传动稳定性有借鉴意义。