制导火箭弹一维稳定平台控制系统设计与分析
杨 煜,赵河明,彭志凌,夏 禹,王 英
(中北大学 机电工程学院,太原 030051)
1 引言
制导火箭弹在飞行过程中弹体是处于旋转状态中的,故弹内制导装置也随之旋转。这会使得惯性测量单元会跟随弹体沿纵轴发生连续滚转,从而影响弹内制导装置制导效果影响命中精度。另一方面,传统的PID控制方法与传感器反馈系统不能满足于对于现代化制导火箭弹的控制需求,且在实际应用中会存在很多偶尔故障,最终影响其对目标的精准打击。在制导武器的头部安装稳定平台系统可以保证制导探测设备能够精准地对目标进行瞄准与打击[1]。一维稳定平台可以使被控制载体在惯性空间的位置保持稳定状态,使载体能够达到精确制导[2]。近年来一维稳定平台系统在现代武器领域中得到了广泛应用。国内对于制导火箭弹应用一维稳定平台的新型控制技术的研究正处于起步和加速的阶段。长春光机所与哈尔滨工业大学对于制导火箭弹一维稳定平台进行了基础的理论分析与研究;南京理工大学姜丽辉对小成本简易制导火箭弹一维稳定平台使用了永磁同步电机三闭环矢量控制的研究;但这些均不适合与多因素下运转的制导火箭弹[3]。
本研究设计了一种实用性高的一维稳定平台控制系统,以此系统实现火箭弹体隔离滚转效果。永磁同步电机(PMSM)具有体积小、运行效率高、承载能力高、转矩脉动小等优点,日前于制导火箭弹中得到广泛应用[4]。故本文选用永磁同步电机作为一维稳定平台控制系统驱动电机,然对于PMSM控制理论来说,传统的PID控制方法与闭环控制系统已经不能满足于对于现代化制导火箭弹的控制需求,且在实际应用中会存在很多偶尔故障,因此研究高性能的PMSM无速度传感器控制方法具有重要意义。
目前高性能的PMSM无速度传感器控制方法主要分为3种,其中一种是滑模观测器法,此算法易于实现且鲁棒性强,得到广泛应用,但发现电机于低速运转中存在相位延迟、抖振与估算精度低的问题;另一种是在同步旋转坐标系下注入高频正弦电压信号,其能够实现在低速段极大改善滑模观测器的弊端,精确结算转子位置转速信息;最后一种是模型参考自适应法(MRAS),能够实现观测误差实现边界层收敛至零,提高了估算精度且能够抑制抖动。为了实现制导火箭弹一维稳定平台控制系统的高性能控制,利用Matlab/Simulink分别建立3种方法的仿真模型并分别应用于3个不同的电机,且对系统进行实验仿真,为系统的实际应用提供了验证。
2 一维稳定平台控制系统工作原理
设计制导火箭弹一维稳定平台控制系统由平台所需机械结构、驱动电机(上舵机、横舵机、下舵机)、控制模块、驱动模块与反馈平台位置信息的位置传感器组成,其中驱动电机由上舵机、横舵机与下舵机组成。上舵机与横舵机选用凸极型永磁同步电机,下舵机选用绕线转子型永磁同步电机,控制模块采用DSP和FPGA的控制架构,并对其3个永磁同步电机分别采用改进型滑模观测、高频脉振电压信号注入法与模型参考自适应法的无速度传感器矢量控制方法。一维稳定平台控制系统工作过程为:首先通过位置传感器监测出一维稳定平台实时位置信息,将此信息输入到控制模块,控制模块将实时位置与给定位置进行比较,得到控制量速度大小,然后根据位置信息提取到实时,将实时速度与给定速度进行比较得到电流控制量与实际电流大小进行对比,最后应用控制模块得到控制信号,应用驱动模块驱动电机对一维稳定平台进行控制调整,从而使得制导火箭弹能准确命中预设目标。一维稳定平台总体结构框图如图1。

图1 一维稳定平台控制系统整体结构框图
3 一维稳定平台控制系统数学模型
为了研究一维稳定平台控制系统,对系统与系统控制算法进行数学建模分析。
3.1 PMSM数学模型
永磁同步电机是一种非线性系统,它具有高阶、多变量、强耦合等特点,三相坐标系下所建立的永磁同步电机模型参数往往具有强耦合性和非独立性的,一般采用Clark变换与Park变换等坐标变换方法将其三相模型转化为两相模型,从而简化PMSM的参数关系[5]。本研究对一维稳定平台控制系统3个舵机均采用表贴式三相PMSM,假设在不影响整体性能的情况下忽略不计电机磁路饱和现象以及磁滞损耗与涡轮损耗[6],采用id=0的控制方法,在d-q坐标系下搭建PMSM。三相表贴式PMSM数学模型表达式为:
式中:ud、uq分别为dq轴电压;id、iq分别为dq轴电流;Ld、Lq为定子dq轴电感;R为定子电阻;ωe为转子电角速度;ψf为永磁体磁链。对于所采用的表贴式永磁同步电机,其交轴与直轴等效电感相等,dq坐标系下磁链方程为:
PMSM的电磁转矩方程为:
Te=np(ψdiq-ψqid)=np[ψfiq+(Ld-Lq)idiq]
式中:Te为电磁转矩;np为电机的极对数。永磁同步电机的运动方程为:
式中:TL为负载转矩;J为电机的转动惯量。
3.2 PMSM无速度传感器矢量控制
PMSM的无速度传感器矢量控制其本质在于不使用位置传感器,通过检测PMSM电机的电压与电流来估算转子的位置,从而能够对转子的磁场进行定向控制。一维稳定平台采用3个电机进行控制,设计上舵机采用改进型滑模观测器无速度传感器矢量控制方法、横舵机采用高频脉振电压注入法无速度传感器矢量控制方法、下舵机采用模型参考自适应法无速度传感器矢量控制方法。
3.2.1改进型滑模观测器无速度传感器矢量控制
一维稳定平台中上舵机应用表贴式凸极型永磁同步电机对其采用改进型滑模观测器的控制方法。滑模观测器法是通过给定的电流与反馈电流之间的误差设计出滑模观测器(SMO),误差可以构造电机的反电动势以此估算电机转子速度与转子位置信息。SMO的估算转速为:
式中:ωeq为SMO估计转速PMSM的控制信号是一种不连续的高频切换信号,因为引入低通滤波器滤除高频信号,然而在利用低通滤波器计算PMSM估计位置信号时会造成一定的位置角度相位移动误差,故需对其进行相位补偿[7]。SMO估算位置表达式为:
式中:θeq为SMO估算的位置信号;ωc为低通滤波器截止频率。改进型滑模观测器设计原理如图2所示。

图2 改进型滑模观测器设计原理图
3.2.2高频脉振电压信号注入法无速度传感器矢量控制
一维稳定平台控制系统中横舵机采用表贴式凸极型永磁同步电机使用高频脉振电压信号注入的控制方法。该方法是在同步旋转坐标系下向坐标系直轴注入高频正弦波信号,使得电机产生电机磁饱和效应,造成交轴与直轴电感不相等,交轴电流中因此含有电机转子的位置信息[8]。为了减小电机的转矩脉动,给估计的同步选择坐标系轴注入脉振高频电压信号,脉振电压表达式为:

式中:L=(Ld+Lq)/2为dq轴电感增量的共模向量,ΔL=(Ld-Lq)/2为dq轴电感增量的差模向量。在经过一定的信号处理方式滤除信号中的高频成分,然后保留并提取其中含有电机转子位置估计误差角的低频信号。高频脉振电压信号注入法使用带通滤波器滤除基频电流分量,以此得到电流信号并对电流信号进行调幅,然后使用低通滤波器提取电机转子位置估计误差角的低频信号[9]。其表达式为:

图3 高频脉振电压信号注入法实现原理图
3.2.3模型参考自适应法无速度传感器矢量控制
一维稳定平台控制系统中横舵机采用绕线转子型永磁同步电机使用模型参考自适应(MRAS)的控制方法。模型参考自适应法将PMSM作为参考模型,首先设置参数可调整模型,使得参考模型与可调整模型具有相同的电压、电流以及转速,然后进行自适应调节,直到2个模型差值为零即可,参考自适应观测器(MRAS)即实现参考模型与可调参考模型误差之间的调整[10]。
建立电机转速自适应律表达式为:

运行过程中满足且动态误差稳定,为提高电机转速估计精度[11],采用MRAS观测器得到:
模型参考自适应法实现原理如图4所示。

图4 模型参考自适应法实现原理框图
4 一维稳定平台控制算法仿真结果分析
在Matlab/Simulink环境对上舵机PMSM采用的改进型滑模观测器无速度传感器矢量控制方法建立模型进行验证;对横舵机PMSM采用高频脉振电压信号注入的无速度传感器矢量控制方法建立模型进行验证;对下舵机PMSM采用模型参考自适应的无速度传感器矢量控制方法建立模型进行验证。
4.1 上舵机PMSM采用改进型滑模观测器矢量控制仿真
上舵机PMSM搭建改进型滑模观测器矢量控制仿真模型采用凸极型电机,PMSM电气参数如表1所示。

表1 PMSM的电气参数
给定转速为800 r/min,仿真结果如图5、图6所示。

图5 转速为800 r/min时的估算转速与实际转速曲线

图6 转速为800 r/min时的估算位置与实际位置曲线
由仿真结果可知采用了改进型滑模观测器算法,滑模观测器估计的转速及位置与实际转速及位置基本重回,电机未出现高频抖动的现象,但是存在局部振荡和一定的误差。故需在横舵机PMSM加入高频脉振电压信号注入矢量控制来获取较高转速与位置精度,且使得控制系统受到逆变器等非线性因素影响较低[12]。
4.2 横舵机PMSM采用高频脉振电压信号注入矢量控制仿真
横舵机PMSM搭建高频脉振电压信号注入矢量控制模型采用凸极型电机,PMSM电气参数如表2所示。

表2 PMSM的电气参数
给定转速为100 r/min,仿真结果如图7、图8所示。

图7 转速为100 r/min时的估算转速与实际转速曲线
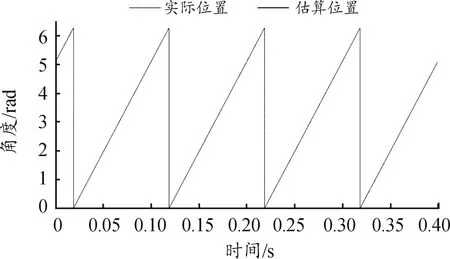
图8 转速为100 r/min时的估算位置与实际位置曲线
由仿真结果可知,使用的PMSM额定转速为2 200 r/min,然而给定转速100 r/min已经使得PMSM转子处于是极低转速段,由图7所示在低转速情况下,使用高频脉振电压信号注入法的控制方法使得转速基本稳定,估算转速及位置与时间转速及位置基本吻合,且振荡幅度较小,极大地改进了上舵机采用滑模控制器控制方法的弊端,使得整个一维稳定平台系统可支持弹体低速运转并准确进行控制。但是,由图可以发现该方法仍存在收敛时间太长、动态性能比较差与稳定范围较小等问题[13]。故需在下舵机PMSM采用模式参考自适应的控制方法来解决这一问题。模式参考自适应法可对PMSM参数进行准确辨识,完成对PMSM的实时监测与控制,以此且在高低速综合适用,弥补了上述2种方法的不足之处[14]。
4.3 下舵机PMSM采用模型参考自适应矢量控制仿真
下舵机PMSM搭建模型参考自适应矢量控制仿真模型采用绕线转子型电机,PMSM电气参数如表3所示。

表3 PMSM电气参数
给定转速1 500 r/min,仿真结果如图9、图10所示。
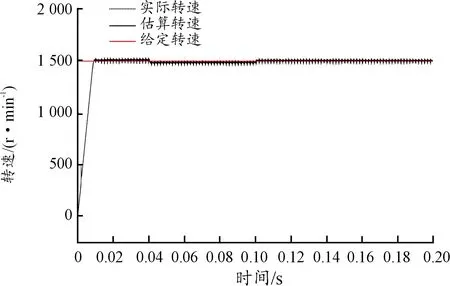
图9 转速为1 500 r/min时的给定速度、估算速度与实际速度曲线
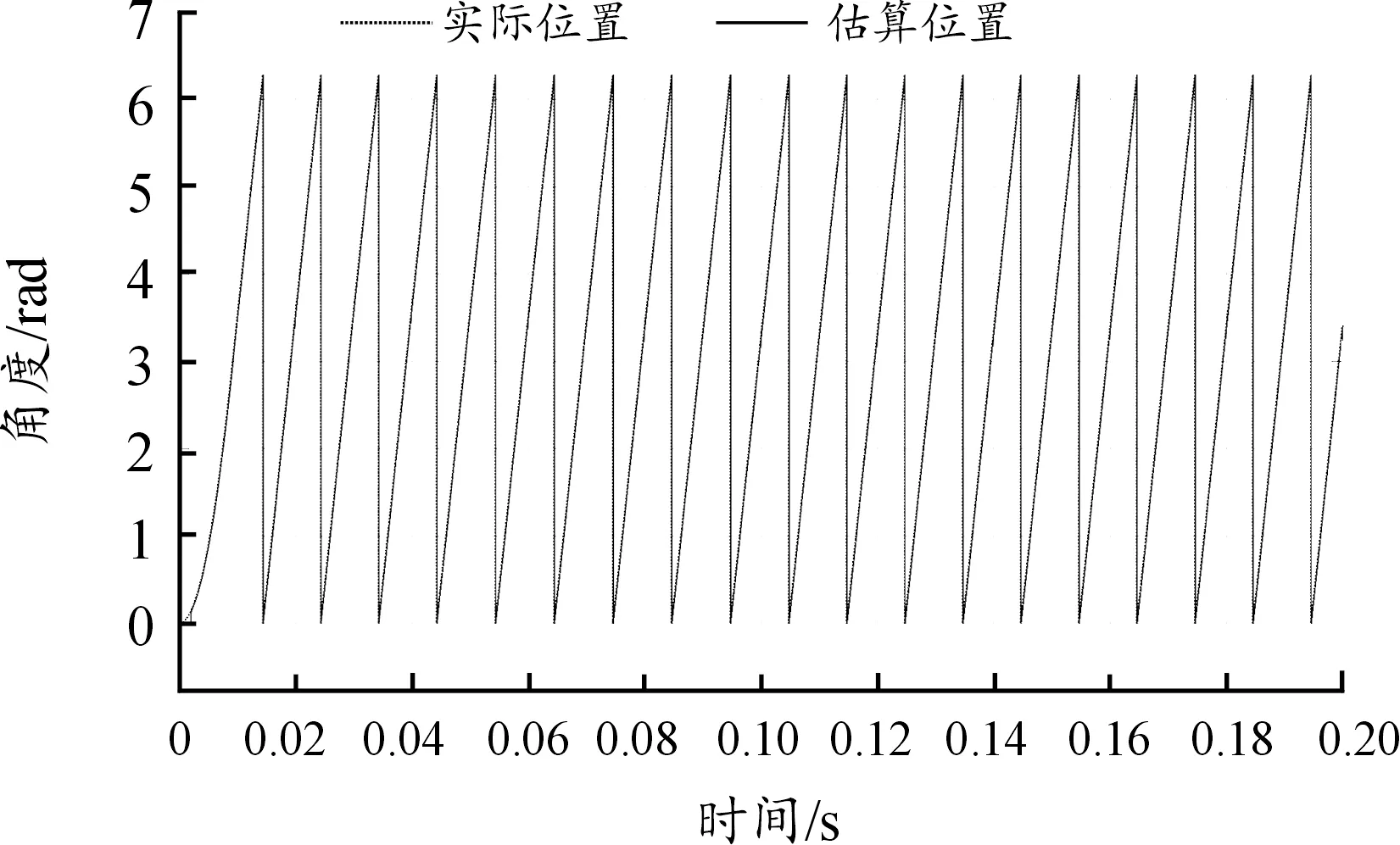
图10 转速为1 500 r/min时的估算位置与实际位置曲线
由仿真结果可知采用模型参考自适应的控制算法,MRAS观测器所估算转子速度及位置与实际转子速度及位置几乎完全相同,略有波动。于控制系统下舵机采用此控制方法补充并改进了上述2种控制方法的弊端且能使得一维稳定平台系统随着运动状态的不同进行自适应地控制。
5 一维稳定平台试验测试与分析
为了验证本文所设计制导火箭弹一维稳定平台控制系统的可行性,本文搭建了DSP+FPGA的一维稳定平台控制调试系统,实验平台包括上位机、供电电源以及上述一维稳定平台控制系统。上位机发送指令通过驱动模块发送控制指令,以此测试整个系统的性能。
实验测试测试高转速下上舵机PMSM估计转子转速的情况,给定2 000 r/min时结果发现电机估计转子能够紧紧跟住实际转速且误差较小;测试中等转速下横舵机PMSM估计转子转速情况,给定1 500 r/min时结果显示电机转子转速在经过较短时间后能够紧密与实际转速重合,误差几乎为零;测试低转速下下舵机PMSM估计转子转速情况,给定100 r/min时结果显示电机转子转速与实际转速从开始到结束几乎完全纯合。3次实验测试结果如图11、图12、图13所示。

图11 高转速估计转速波形

图12 中等转速估计转速波形
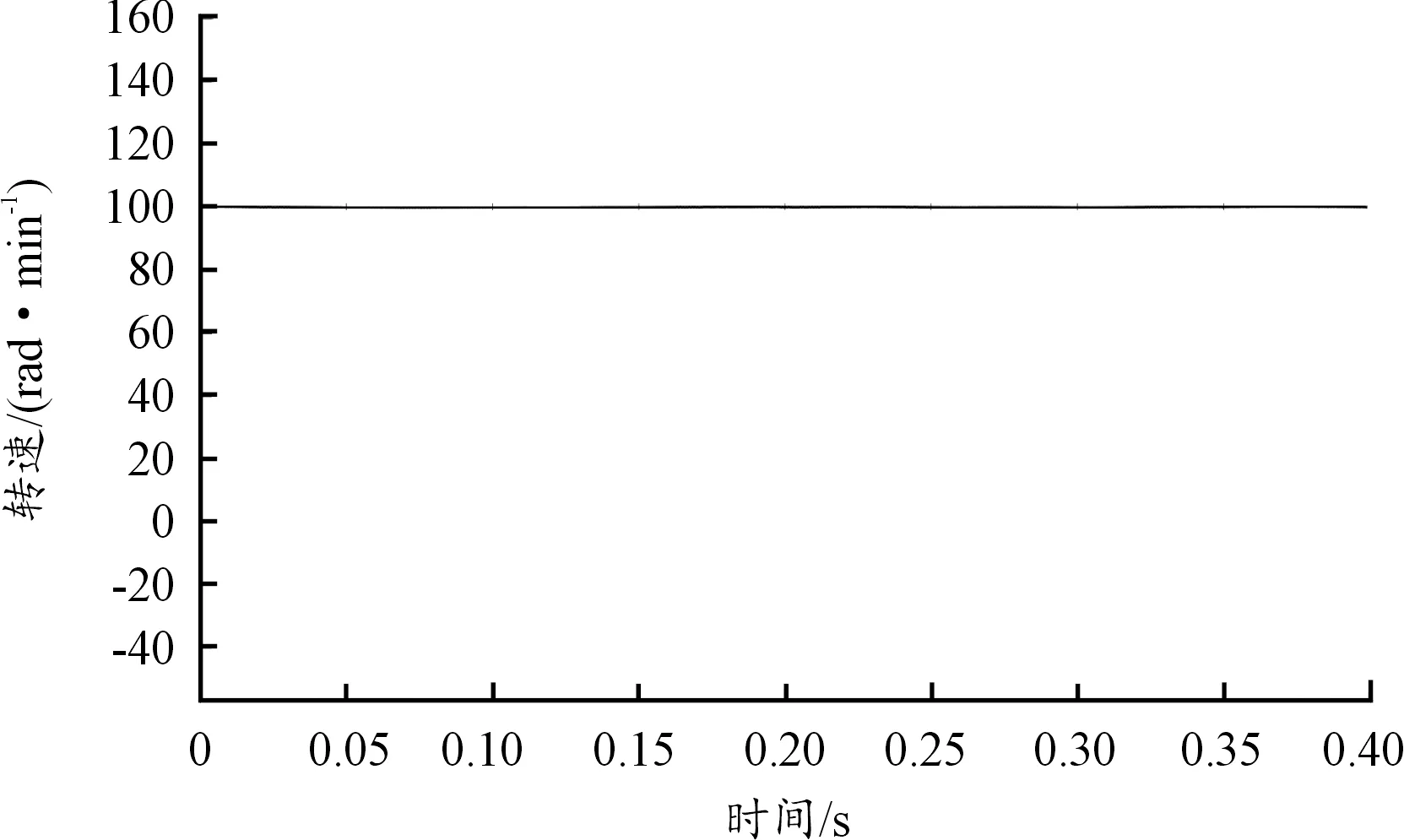
图13 低转速估计转速波形
为研究制导火箭弹一维稳定平台采用上横下三舵机控制系统的控制性能,另外搭建单舵机采用传统的PMSM三闭环位置反馈控制系统与三舵机无速度传感器控制系统进行对比。其中PMSM参数与表1相同,将给定电机转子位置与实际转子位置进行对比,测试结果图14、图15所示。

图14 三闭环位置反馈控制系统电机实际转子位置与给定位置曲线

图15 无速度传感器控制系统电机实际转子位置与给定位置曲线
由图14可知制导火箭弹一维稳定平台单舵机采用传统的三闭环位置反馈控制系统电机实际转子位置与给定位置一直存在误差,对于速度多变位置多变的制导火箭弹来说有较多的不适合,但本文采用的三舵机无速度传感器控制系统电机实际转子位置与给定位置误差存在较小且趋于相同,适用于制导火箭弹一维稳定平台。
6 结论
1)针对制导火箭弹惯性测量单元在弹体发射后会产生滚转,设计了一维稳定平台控制系统。制导火箭弹舵机采用PMSM,设计上舵机采用改进型滑模观测器控制,横舵机采用高频电压信号注入控制,下舵机采用模型参考自适应法控制。
2)PMSM在低中高速运行稳定,克服了单一方法所产生的较大误差与高频抖动的现象,使得控制精度更高,性能更加优越。
3)一维稳定平台控制系统3个舵机分别在高中低速控制性能较好,对整体性能进行分析对比。
4)本文对一维稳定平台控制系统的设计仍处于理论研究与原理实现阶段,后续研究应使控制系统更好地适应实际情况。

