舰载机牵引系统舰面转运动态避碰研究
朱兴动,韩啸华,范加利,王 正
(1.海军航空大学,山东 烟台 264001;2.海军航空大学青岛校区,山东 青岛 266041)
1 引言
舰载机是航母战斗力的体现,其在甲板上的转运策略是舰载机综合出动能力的直接影响因素之一[1]。作为舰载机出动和着舰回收流程的重要组成部分,由牵引车和舰载机构成的牵引系统需要在飞行甲板障碍密集和空间紧凑的情况下进行平面移动,以适配相应的保障站位和起飞站位。
随着信息技术的发展,各国相继通过计算机平台对舰载机甲板布列调运策略进行模拟,如美军目前正在使用的航空数据管理与控制系统(aviation data management and control system,ADMCS)[2],该系统能够实时监控舰载机的布列调运情况。国内王国庆等[3]也对甲板调度路径优化问题进行了相关研究。
舰载机在舰面上的转运可看作平面内移动机器人的避碰规划问题。移动目标的避碰规划问题经过多年来的研究已经发展成熟,如行为动力学法[4-5]、遗传算法[6-7]和粒子群算法[8-10]等。为了简化避碰过程,多数算法将机器人简化为质点或圆形,并且在进行规划时不考虑转弯约束,直接以折线或曲线作为有效路径。而舰载机形状复杂,存在尖角,特别是在收翼状态下,机身细长,若将其视为圆形,则会浪费大量空间。此外,由牵引车和舰载机构成的牵引系统复杂,规划的路径也需要考虑到运动学约束。
本文以此类问题作为研究背景,提出了一种适用于复杂目标形状在障碍密集环境下的避碰方法。该方法以动态窗口算法为基础,针对舰面环境提出了改进方法,同时设计了动态优先级分配策略,有效解决了牵引系统舰面转运的避碰问题。
2 舰载机形状描述及距离计算
2.1 舰载机轮廓描述
在甲板转运过程中,舰载机需要根据任务要求在展翼和收翼状态中进行切换,因此本文对舰载机的2种状态进行轮廓描述。为了降低模型复杂度,在包含舰载机轮廓且不损失较多有效空间的前提下,引入多边形线段集来进行描述,如图1所示。

图1 舰载机轮廓示意图
2.2 碰撞距离计算
实现舰载机的碰撞检测需计算舰载机之间的安全距离,被多边形线段集描述后的舰载机形状为凸多边形,故问题实质转化为求解凸多边形间的最小距离。给定两个非连接的凸多边形P和Q,本文按照如下步骤来推导凸多边形间最短距离,如图2所示。
步骤1计算P上纵坐标值最小的定点yminP和Q上纵坐标值最大的定点ymaxQ。
步骤2过yminP和ymaxQ构造两条具有相反方向的平行切线LP和LQ,使得对应的凸多边形位于切线的右侧。
步骤3计算yminP和ymaxQ两点之间的距离dPQ。
步骤4顺时针同时旋转两条平行线直到其中一条与边线重合。
步骤5判断:若切线没有与边重合,则计算点到点的距离,如图2(a)所示;若只有一条平行线与边线重合,则计算点到线的垂直距离,如图2(a)所示;若两条切线都与边重合,则计算边到边的垂直距离,如图2(c)所示。将计算结果与当前值比较,若小于当前值则更新dPQ。
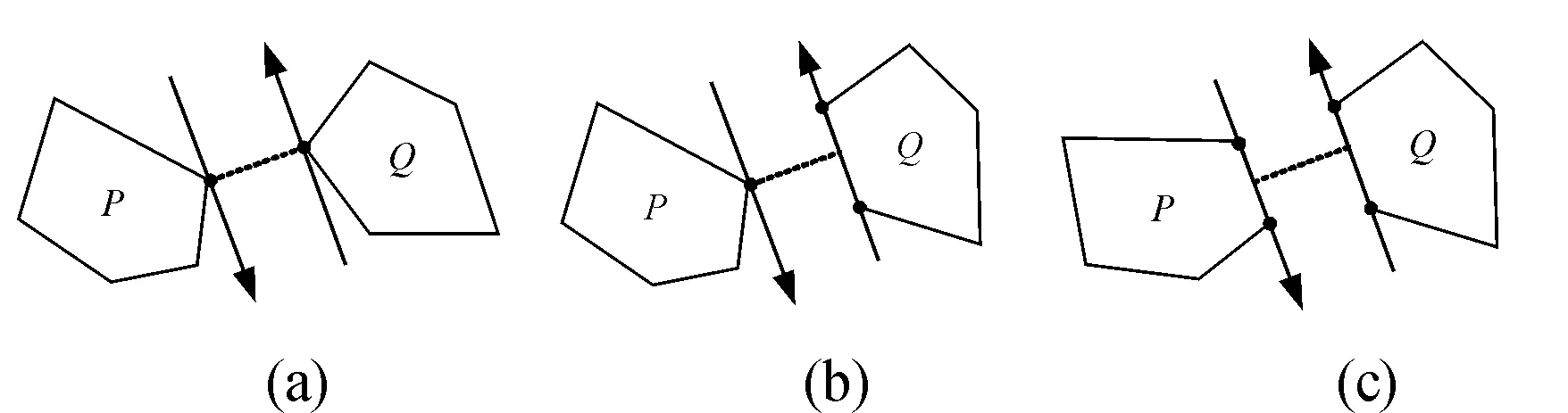
图2 碰撞距离检测示意图
步骤6重复执行步骤4和步骤5,直到输出最小值。
3 牵引系统运动学模型分析
舰面舰载机的转运过程可简化为轮式机器人在平面内运动,因此本文针对无杆牵引系统进行分析。在系统中,舰载机前起落架铰接在牵引车后轮中心位置,通过控制牵引车运动进而确定舰载机的移动速度和转弯半径,牵引系统如图3所示。

图3 无杆牵引系统示意图
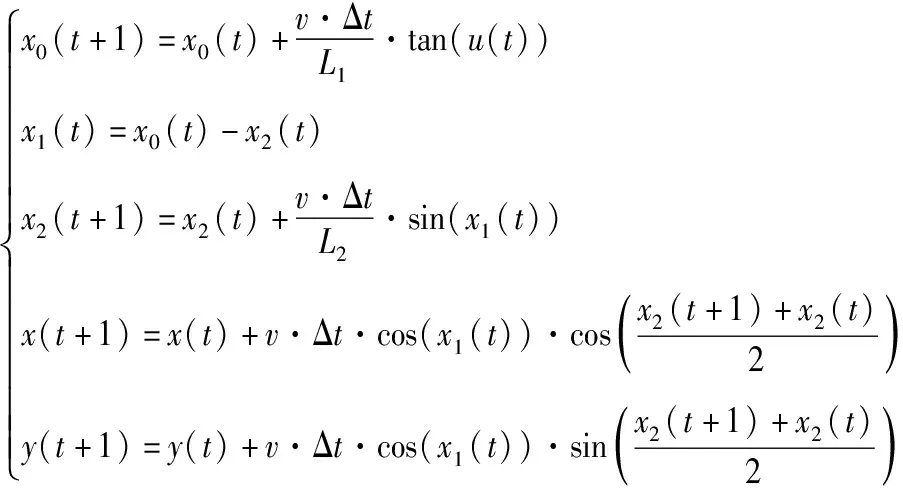
式中,x0(t)表示t时刻牵引车方位角度;x1(t)表示t时刻牵引车和舰载机的角度差;x2(t)表示t时刻舰载机方位角度;x(t)表示t时刻舰载机后轮中心水平位置;y(t)表示t时刻舰载机后轮中心垂直位置。由于牵引系统受轮式结构限制,其运动轨迹受最小转弯半径约束:
r≥rmin
现通过限制最大角速度来约束其转弯半径,且舰载机在舰面转运时速度较小,故对线速度和角速度进行约束:

通过上述关系式,在给定牵引系统速度v、角速度ω、迭代步长Δt、t时刻牵引车角度x0(t)和t=0时刻的舰载机角度x2(t)的条件下,即可计算舰载机的运动学轨迹。对上述模型进行仿真验证,仿真结果如图4所示。

图4 牵引系统运动仿真结果示意图
图4中,红色轮廓代表初始位姿,蓝色轮廓代表目标位姿;给定牵引系统初始速度v=0.1 m/s;迭代步长Δt=0.2 s。通过仿真结果可得出结论:在速度恒定的情况下,牵引系统做满足运动学约束的圆周运动,故实现了舰载机牵引系统的运动学建模。
4 动态窗口算法
4.1 基本原理
动态窗口法是SebastianThrun等[10-12]在1997年提出的一种基于机器人运动学和动力学的局部路径规划算法,该算法从运动学角度出发将动态规划问题转化为速度矢量空间上的约束优化问题。其基本原理是:在一定的时间间隔内,采集目标在二维空间的有效速度(包括线速度、角速度和加速度等),并同时模拟机器人在不同速度下的轨迹,根据设计的评价函数来选取最优轨迹,完成目标的局部路径规划。该算法具有实时性强、计算量小等优点,可有效解决舰载机转运问题。
4.2 速度采样
在获取牵引系统的运动学模型后,就可以根据模型推算出在一定时间内的运动轨迹。在理想的情况下,牵引系统的速度可以有无穷多值,但考虑到舰载机转运约束以及舰面环境条件限制,可将搜索空间缩小到一定的范围内,约束条件主要有以下3个方面:
1)速度约束:在上一节对牵引系统运动学模型分析的过程中,对系统的最大速度和最大角速度进行了约束,故速度矢量空间的约束可以表示为:
Vm={(v,ω)|v∈[vmin,vmax],ω∈[ωmin,ωmax]}
式中,vmax和ωmax为最大线速度和最大角速度;vmin和ωmin为最小线速度和最小角速度,在舰面转运过程中可取值为0。
2)动力学性能约束:牵引系统的最大加速度受舰面转运条件约束,故在模拟周期Δt内的线速度和角速度的窗口范围为:
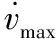
3)安全约束:舰载机与障碍物发生碰撞前,需确保以最大加速度值进行减速的条件下能够将减速到0,故对牵引系统的线速度和角速度约束为:
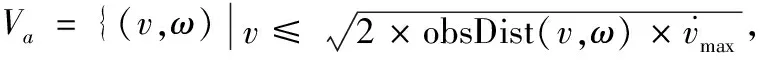
式中,obsDist(v,ω)为速度(v,ω)所对应轨迹与最近障碍物之间的最短距离。通过该约束来计算模拟轨迹是否合理,若不合理则舍弃该条轨迹。
综合上述约束条件,舰载机的速度矢量空间表示为:
V=Vm∩Vd∩Va
4.3 评价函数
速度矢量空间内的每一个速度(v,ω)都代表一条模拟轨迹,因此,需要设计评价函数来对模拟轨迹进行评价,并选取最优的轨迹。比较经典的评价函数为:
G(v,ω)=σ(α·heading(v,ω)+β·obsDist(v,ω)+
γ·velocity(v,ω))
式中,heading(v,ω)为航向角函数,用于评价模拟轨迹末端航向与目标位置之间的角度差,差值越小,评价越高;obsDist(v,ω)为障碍距离函数,用于评价模拟轨迹末端与障碍物之间的最短距离,距离越大,评价越高;velocity(v,ω)为速度函数,用于评价模拟轨迹对应的速度大小,速度越大,评价越高;α、β、γ表示3个评价标准的权重。为避免某一项评价因子的值过大而造成的该因子优势太大,引入σ来对3项参数进行归一化处理,进而选取综合评价最高的轨迹。
4.4 算法改进
在仿真过程中发现,当牵引系统在接近目标点时,由于航向与目标位置角度差较大,系统会在航向角函数的影响下增大角速度,这会导致牵引系统行驶不稳定,容易产生绕行现象,导致路径规划失败,如图5所示。

图5 绕行现象示意图
为此,本文设计了新的评价函数:
G(v,ω)=σ(α·goalDist(v,ω)+β·safeDist(v,ω))
式中,goalDist(v,ω)为目标距离函数,该函数用于评价模拟轨迹终端与目标位置之间的距离,来取代航向角函数,消除航向角偏差较大导致的绕行现象;safeDist(v,ω)为安全距离函数,该函数将速度采样中的安全约束与障碍距离函数结合,用于评价模拟轨迹终端与障碍物之间的安全距离,表达式为:
safeDist(v,ω)=max[brakDist(v,ω)-obsDist(v,ω),safeDist]
式中,brakDist(v,ω)为最大加速度下进行减速所需要的距离;safeDist为目标与障碍物之间的最小安全距离常数。
由于的改进后评价函数已将安全约束考虑进去,因此速度窗口仅由速度和动力学性能约束限制,表达式为:
V=Vm∩Vd
5 优先级策略
舰载机的动态避碰行为与避障行为类似,当舰载机检测到其他舰载机时,可将其视为障碍物进行避碰,但由于舰面空间有限,彼此互相避让会浪费较多有效空间,因此本文设计了一种动态分配优先级策略,当舰载机进入碰撞距离时,优先级高的舰载机优先转运,优先级低的舰载机视优先级高的舰载机为障碍物,并主动避让,动态分配优先级示意图如图6。
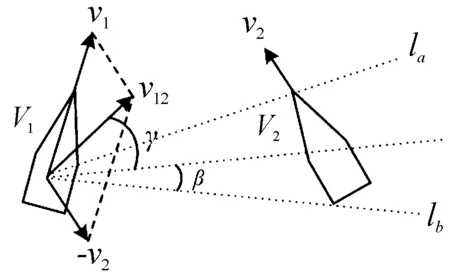
图6 动态分配优先级示意图
令v1和v2分别表示舰载机V1和V2的速度,则V12=V1-V2表示相对速度,假定V1的速度为V12,则V2可看做是静止。作V1到V2顶点的射线la与lb,并确保V2在射线所夹的范围内。将la与lb所成锐角记为α,令β=α/2,γ是v12与V1V2之间的夹角,若γ≤β,则必会发生碰撞。故记γ≤β的逻辑值为Rvi,若其成立则取值为1,反之取0。Rvi式为:

此外,舰载机的优先级也与当前的任务有关,通常出动任务较入库任务具有更高的优先级,故记转运任务的逻辑值为Lvi,若取值为1则代表出动任务,反之取0。Lvi式为:
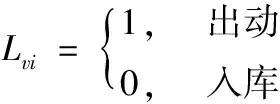
此处仅列举了两个优先级策略,在实际转运过程中,可根据舰面实际情况进行设计。综上,序号i舰载机优先级Vi定义为:
pi=∑(Rvi+Lvi)
6 仿真
给定牵引系统速度最大线速度vmax=1 m/s、最大角速度ωmax=0.5 rad/s、迭代步长Δt=1 s,通过Matlab对改进后的算法进行仿真。红色轮廓和青绿色轮廓代表起始位姿,黑色轮廓代表转运过程中的位姿,蓝色轮廓代表终点位姿。运动轨迹残影描述了系统碰撞检测外轮廓,轮廓密集处体现了速度约束与动力学性能约束的作用。设定红色轮廓舰载机的优先级最高。
图7(a)与7(b)为收翼状态和展翼状态下的单机避碰仿真;图7(c)与图7(d)为收翼状态和展翼状态下的多机避碰仿真。
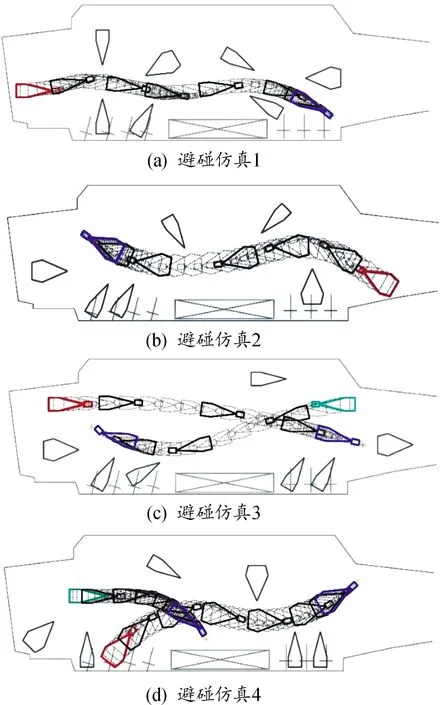
图7 牵引系统路径规划仿真图
由于,如(a)图、(c)图的最左边,(b)图的最右边,(d)图下排的最左边舰载机的优先级较(c)图上排的最右边和(d)图上排的最左边舰载机的优先级高,可以看到当舰载机即将碰撞时,图7(c)上排的最右边舰载机进行了主动避障行为,图7(d)的上排的最左边舰载机进行了减速行为。由此可见,本文算法能很好地解决舰面牵引系统的动态避碰问题。
7 结论
提出了一种适用于复杂形状目标的动态避碰方法。以动态窗口法为基础,针对避碰规划,对评价函数进行了改进。为提高多机环境下的避碰能力,提出了可动态分配的优先级策略。Matlab仿真结果表明,改进后的方法能够有效解决舰载机牵引系统舰面转运动态避碰问题,同时也可为其他类似形状的复杂目标避碰规划提供参考。

