基于灰色预测模型的板形PID控制器优化仿真与应用

王海霞，尤凤翔，张 兵

(1.苏州大学应用技术学院，江苏 苏州 215325；2 江苏大学机械工程学院，江苏 镇江 212011)

1 引言

目前科技及经济的发展使有色金属的应用领域不断拓宽，尤其是对高质量的铝板带材箔需求增大，市场对产品质量提出了更高要求，而板形作为板带材最主要的质量指标之一，影响着板带材最终成品质量，随着板带材生产技术水平的提高，带材的宽厚比越来越大，造成生产设备复杂庞大，使板形控制技术变的困难和复杂。尤其当前金属加工处于由量向质的转变过程中，高精度板形控制成为轧制设备、工艺和控制领域研究者必须面对的课题和目标。

铝板带材轧制过程中板形控制系统受张力、板厚、板凸度、轧制力、弯辊力、辊温度等诸多因素影响，具有较大的非线性特性，受轧制工艺和条件的限制，板形检测装置(板形仪)必须安装在轧机出口侧，距离轧辊中心有一定的距离，造成检测和控制之间存在实测数据的滞后；板形缺陷调整装置具有惯性特点，这两点造成了板形控制参数时变和大滞后的特点，所以常规控制手段很难获得满意的控制效果。

目前常用的控制方法是通过轧制理论，利用数学工具建立起非线性板形被控对象数学模型，进行控制量求解。这种方法很难做到既准确表达各参量之间的静态关系，又准确描述其动态关系的表达式，对板形控制的滞后特性和稳定控制很难做到两全其美[1]。文献[2]采用模糊PID控制器进行板形控制,文献[3]采用动态设定型板形板厚自动控制系统方法对板形进行参数预设定,文献[4]采用基于多元线性回归的板形平直度预测控制研究进行预测控制。这些控制方法并不能从根本上解决板形控制的滞后特性和稳定控制。

本文在深入研究灰色预测理论[6]的基础上，对灰色预测模型控制器进行了优化改进，该优化策略利用灰色预测模型较强的自适应性，结构简单实时性好的优点，同时采用滚动优化[12]策略避免灰色预控模型对建模维数及步长数的特殊要求，同时在轧制进入稳态状态后切入Smith预估方法代替灰色预估。通过这种改进策略进行板形测量值的预测和板形控制。这既能利用灰色预测模型的预测功能，又能克服因模型维数太大造成的跟踪性变差，同时实现对实测数据的滤波作用，并且在稳态轧制时用Smith预估代替灰色预估避免预测值的失准。通过仿真验证，这种方法降低了计算量增加了板形预测的准确性，进一步在某1400铝板带材冷轧机上进行的试验，表明该策略相对于传统方法准确有效，具有较快的响应速度、较强的鲁棒性和抗干扰能力，减小了动态超调量，板形控制系统的动静态性能和精度都得到了显著提高。

2 板形控制系统

板带材加工中的板形指的是带材的翘曲程度。轧制过程实质是金属坯料在轧辊作用下的塑性变形过程，金属坯料经过轧制会发生明显的纵向延伸和横向流动，当沿横向板宽压下量分布不均时，带材横向分布的各个窄条会相应地发生延伸不均，产生相互作用的内应力，内应力足够大就会引起带材翘曲，常规意义板形就是带材内部残余应力的分布。残余应力分布不均会带来板形缺陷，即通常所说的“波浪”，延伸大的带材受到压应力作用，而延伸小的带材受拉应力作用。当压拉应力达到一定值时，带材产生各种形式的波浪，包括单边浪、双边浪、中间浪、复合浪等，在纵切带材时带材不能保持平直达不到使用要求。带材板形通常采用翘曲度和延伸率来进行描述如图1。

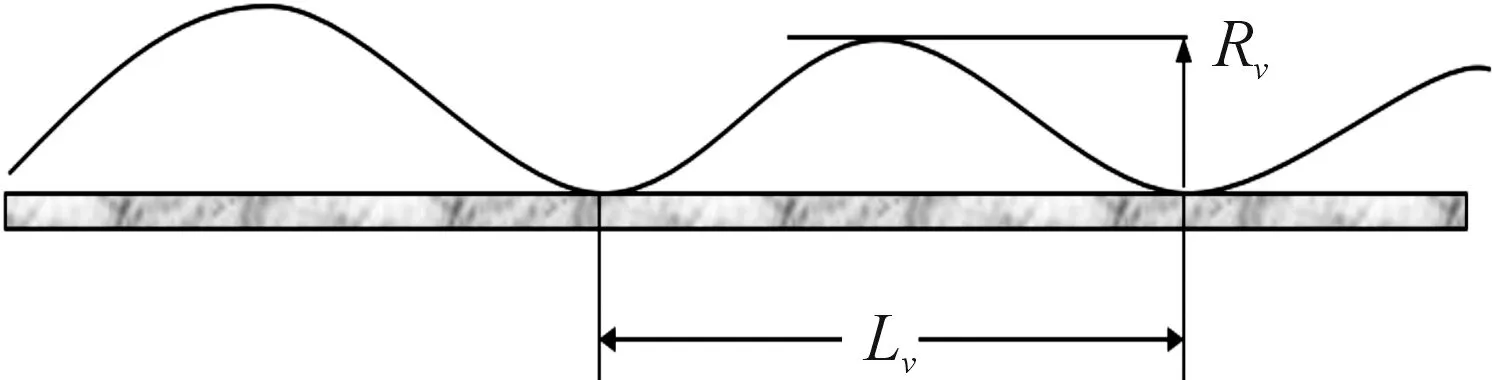
图1 板形翘曲示意图

(1)

理想板带材产品应该是平坦的，为了达到这个目标，除了从轧制工艺和轧机设备上进行板形调整外，最重要的调控手段是板形控制系统对板形缺陷的修正，它包含:一次项的倾斜控制，二次项的弯辊控制和高次项的冷却喷淋等控制手段。通常系统组成有：目标板形设定、板形测量、实测数据处理、板形缺陷模式识别及PID控制器等环节组成。控制系统原理框图如图2。

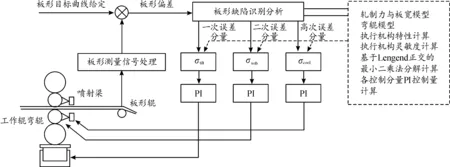
图2 板形控制系统原理框图

板形控制属于闭环控制，如图2所示轧制出口侧板形仪检测到一组实际的板形测量值σi后，通过Profibus总线通讯给板形核心控制器，经板形缺陷模式识别，得到板形各个项次的缺陷曲线参数，与轧制工艺要求的板带材目标曲线相比形成不同调整机构的误差分量，送入相应的调整控制器，经PI调节器输出控制量给轧机控制执行器，由不同调整机构动作，最终实现板带材出口板形的控制。

在板形闭环控制系统中，板形检测装置一般安装在机架出口侧距轧辊2～2.25 m处，轧制过渡过程中板形检测信号和板形控制系统之间的滞后时间大概在5～8个采样周期，明显滞后，导致带材头尾及低速动态轧制时板形控制精度较差[13]。

3 灰色预测模型

在灰色控制理论中模型表示为GM(M,N),M是微分方程的阶数,N是变量个数,常用的灰色预测模型是GM(1,1),含一个输入变量的一阶灰色模型，使用灰色模型预测板形检测张应力数据，需要的原始信息少,计算量小,适用于复杂的动态过程,能够满足对系统的实时控制[10,14]。

板形灰色预测模型控制原理图如图3所示,灰色预测模型的作用是把系统输出σ(k)读入(记做σ(0)(k)),根据灰色预测算法计算,预测一定时间后的输出值σ(0)(k+n),将其代替此刻的σ(0)(k),并与设定值r(k)比较,产生的偏差e(k)作为控制器的输入,控制器的输出u(k)是被控对象的输入。

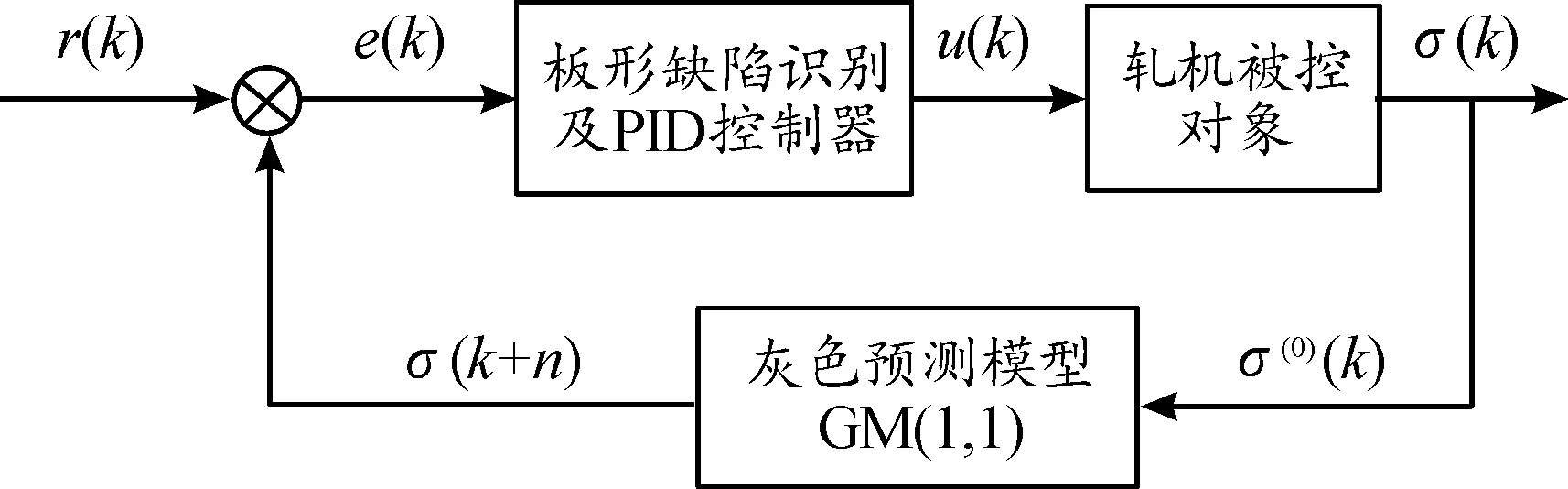
图3 灰色预测控制器控制原理示意图

灰度建模机理和过程如下：

1)选择建模维数n

已知实际测量值为一非负数列σ(k)={σ(0)(1),σ(0)(2),σ(0)(3),…，σ(0)(n)},数列中n为板形实测值组数，用来预测下一组板形张应力值，文献[5]中指出灰色预测模型精度和建模维数有关。工业生产过程波动较大，维数大容易使大量的旧数据掩盖新数据，这样预测对系统的波动反映迟缓跟踪性变差，对控制精度有影响；n过小则预测值的滤波作用变小。因此维数n大部分都选择在5以内。

2)生成累加序列σ(1)

σ(1)={σ(1)(1),σ(1)(2),σ(1)(3),…，σ(1)(n)},其中

(2)

数据序列做累加后测量值中的随机噪声将被滤掉，累加后的数据序列呈指数形式规律。

3)拟合灰色微分方程

σ(0)(k)+az(1)(k)=b,(k=2,3,…,n)

(3)

式(3)中:a为趋势系数，b为灰度模型参数，z(1)(i)=0.5(σ(1)(i)-σ(1)(i-1))，得到GM(1,1)的白化方程：

(4)

令

σ=[σ(0)(2)σ(0)(3)…σ(0)(n)]T

(5)

(6)

则σ=XY，最后用最小二乘法[15]求出y=(XTX)-1XTσ。

4)求解预测值

通过白化方程式(4)可得K+1时刻板形测量值的累加值：

(7)

通过对去除第一点的原始数据进行Mea(k)=Nea(k+1)的拟合，得到原始数据对K+1时刻的预测值为

(1-e-a)[σ(0)(1)-b/a]e-ak

(8)

σ(0)(k+n)=(1-e-a)[σ(0)(k)-b/a]e-ak

(9)

其中(k=1,3,…,n)。

4 灰色预测优化模型PID控制

灰色预测模型从系统实测数据中寻找数据发展规律，着眼于系统未来的行为可进行超前控制，对测量数据呈指数形式或具有惯性环节及大滞后特点的系统，能够克服传统PID控制的局限性和不足之处[7-9]。但在实际应用中发现，灰色预控确定建模维数N和预测步长数M比较困难，需要通过现场不断的实验和调整，尤其步长M对控制性能影响比较大，M过大响应速度慢，过小则输出变化剧烈引起超调增大，比较难精确确定[11]。

为解决这个问题，本文在灰色预测的基础上引入预测滚动优化模型，并和Smith预估相结合在板形稳态生产中也能够进行板形实测值预估，其控制原理如图4所示。取n=4的建模维数，M=2的预测步长，在轧制测量的滞后时间段内进行预测参数滚动优化，即在每一个采样时刻，性能优化参数只涉及从测量点到轧辊辊缝间的板形控制参数，下一个采样时刻，优化时段同时向前推移。以滚动形式反复在线进行，同时根据滞后时间，将采集到的同时刻板形测量值和预测模型值进行对比，通过反馈校正对下一次预测行为加以补偿，利用检测信息构成预测闭环优化，本设计优化后的目标函数表达式如下：

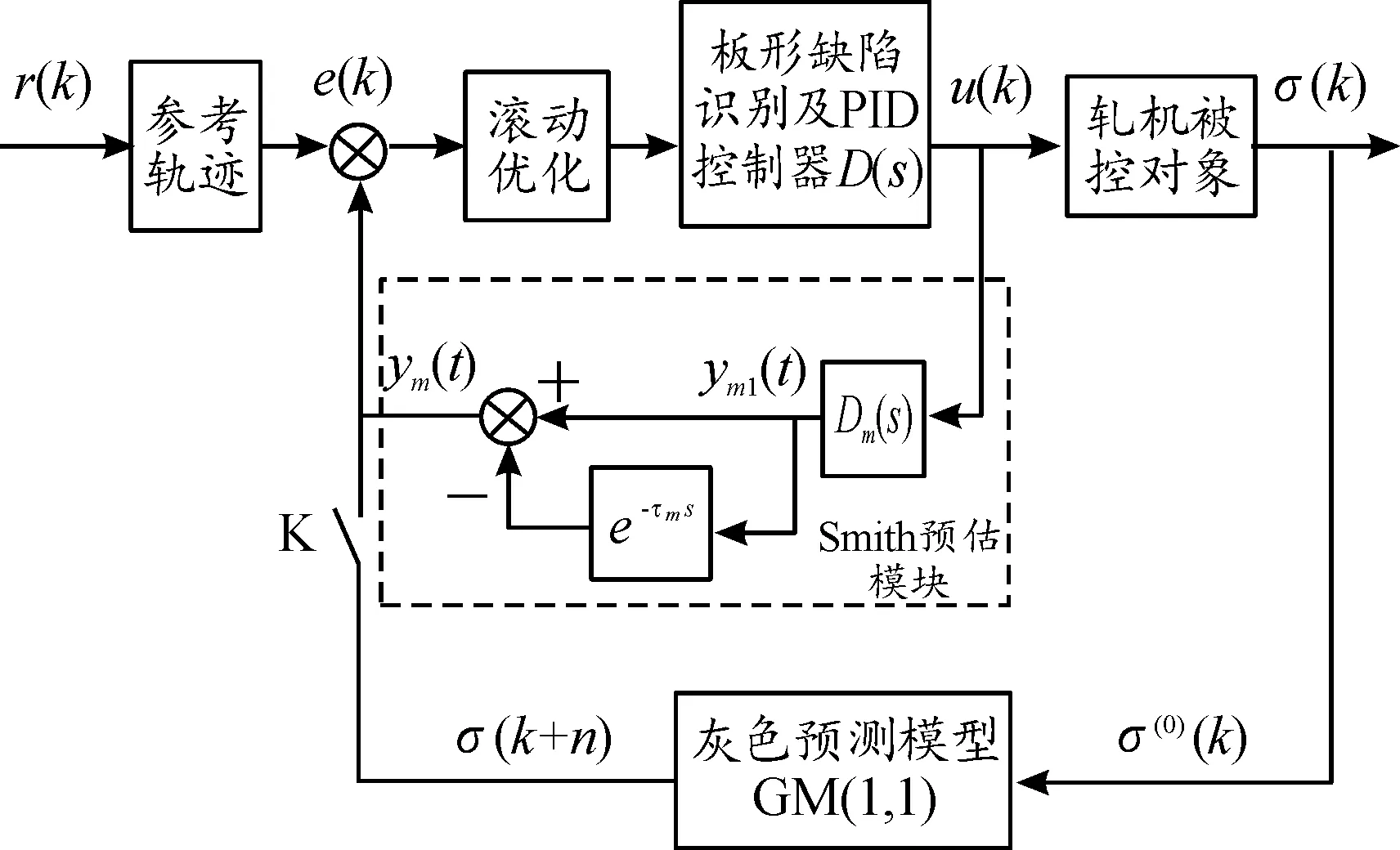
图4 灰色预测优化控制器控制原理示意图

(10)

式(10)中：N为预测时域，M为控制时域，E为系统输出的期望值，σ(0)为板形预测值，σr为板形设定值，wj为板形板宽和轧制力的加权系数，ri为误差加权系数。当j>M时，u(t+i-1)=u(t+M-1)。在优化后，控制并不是输出直接跟踪目标值，而是跟踪参考轨迹，参考轨迹由板形效应函数模型离散成101个离散点组成，根据不同的控制函数组成相应的板形目标评估曲线。

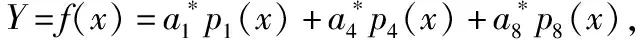
F1=P1(X)=ax-bx7

(11)

F2=-P1(X)=-ax+bx7

(12)

F3=P4(x)=0.125(35x4-c*cos(π(1+x)))

(13)

F4=-P4(x)=-0.125(35x4-c*cos(π(1+x)))

(14)

F5=P8(x)=de(-2(1-fabs(x)))cos(2πx)

(15)

F6=-P8(x)=-de(-2(1-fabs(x)))cos(2πx)

(16)

J(θ)=(F-P(X))T(F-P(X))

(17)

(18)

将分解后的板形控制分量代入式(12)中进行参考轨迹的跟踪：

σr(k+j)=ajσr(k)+(1-aj)σ(0)(k)

(19)

一次板形分量对应PI控制模型为

Y(T)ftilt(t)=(Ctilt+kt(Tdelay+(LRr+LCm)/V))*

(20)

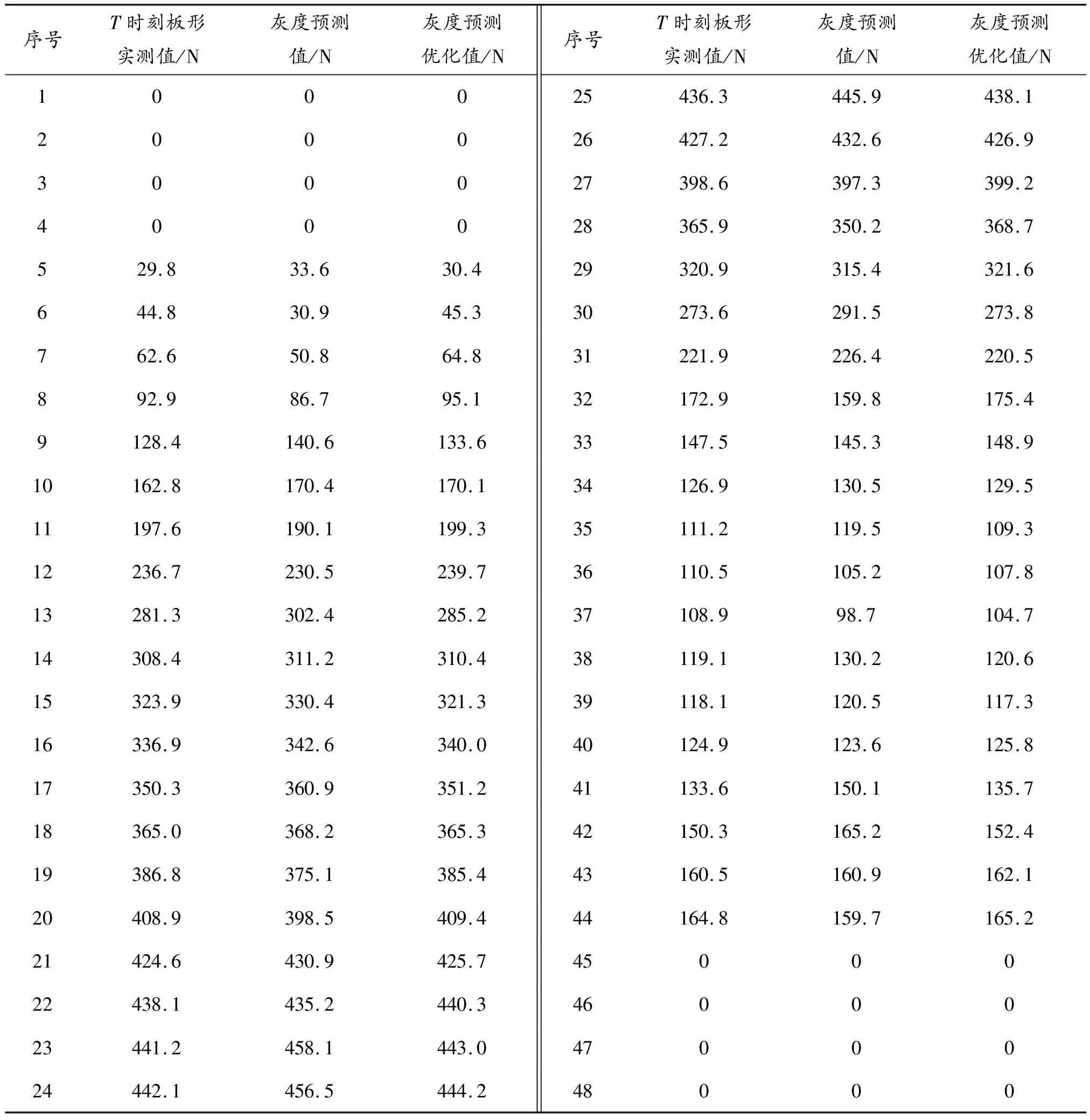
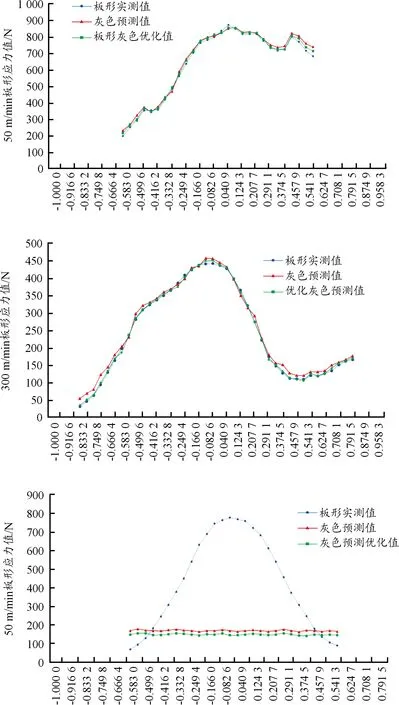
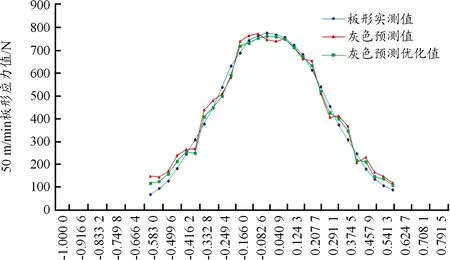
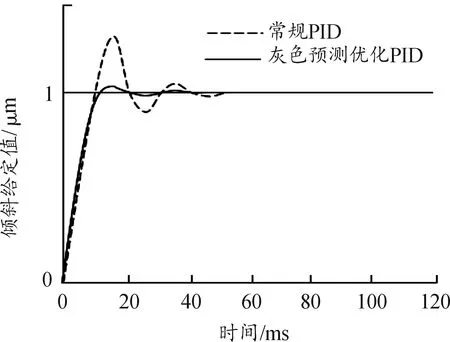
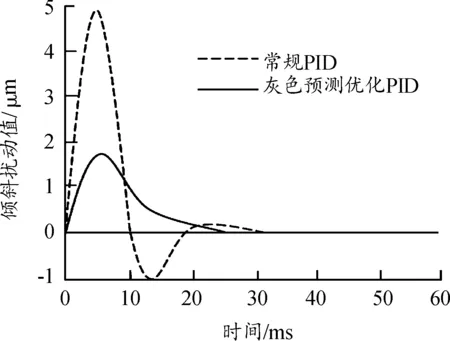
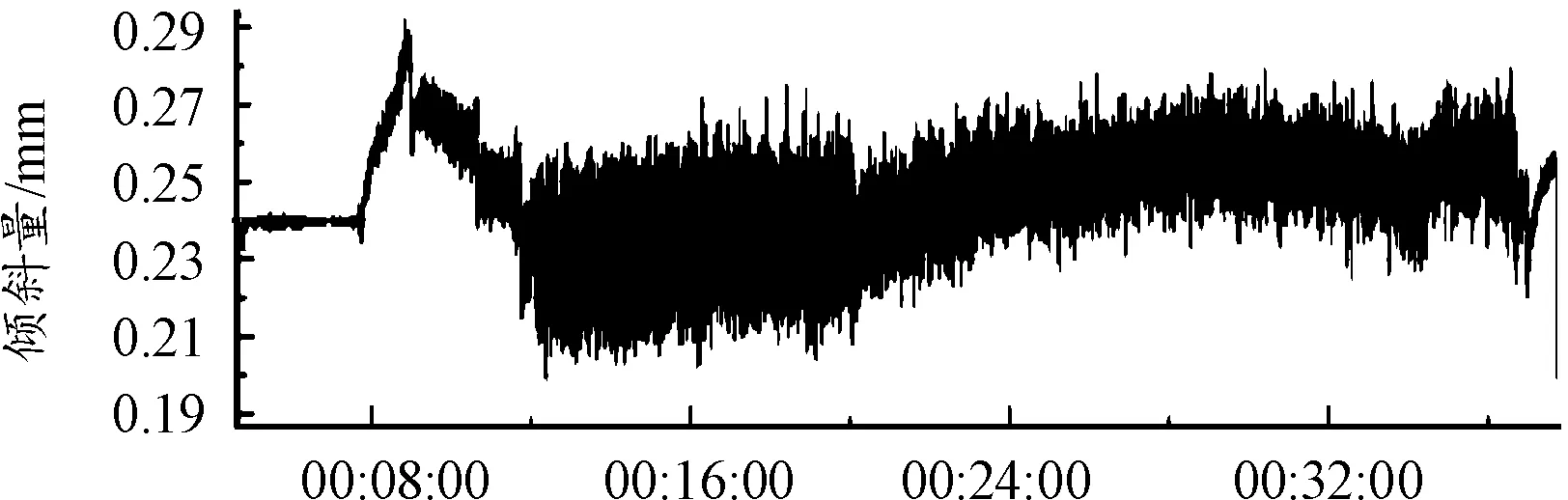
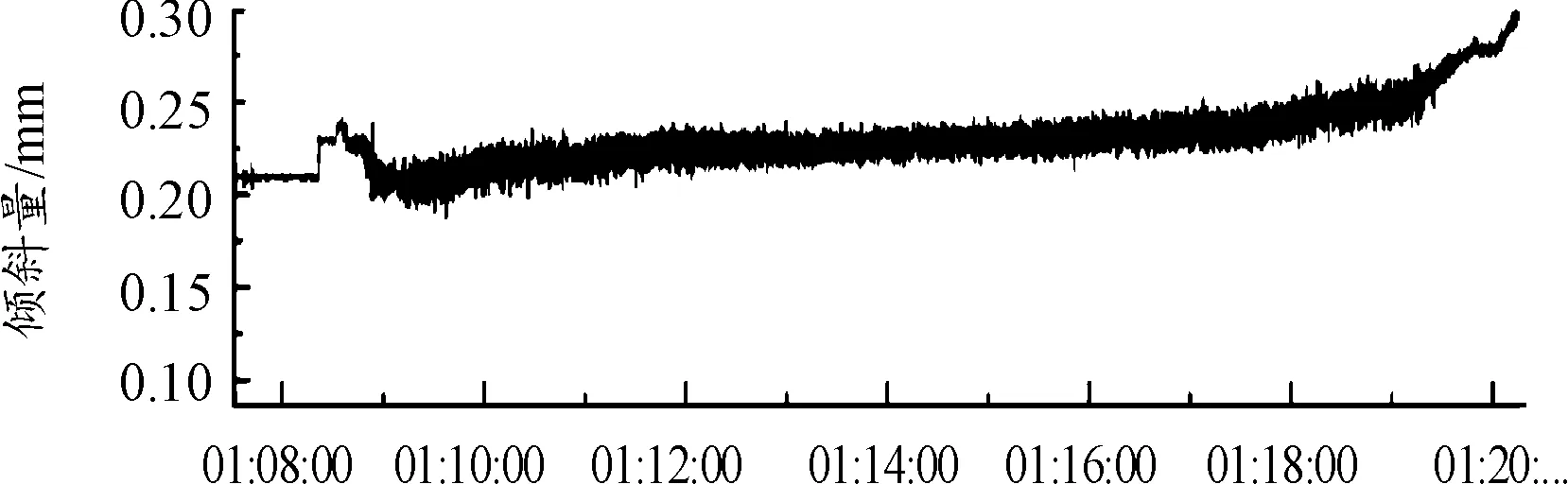
式中：当Ts

ISUM(t)=(Ctilt+kt(Tdelay+(LRr+LCm)/V))*

(21)

当Ts≥Tn时，

(22)

二次板形分量对应PI控制模型为：

Y(T)fwrb(t)=(Cwrb+kt(Tdelay+(LRr+LCm)/V))*

(23)

式中：当Ts

ISUM(t)=(Cwrb+kt(Tdelay+(LRr+LCm)/V))*

(24)

当Ts≥Tn时，

(25)

5 控制系统仿真分析及应用

本文在某1 400 mm铝冷轧机上进行验证，采集板形仪实测数据进行仿真测试，轧机所生产的铝带材卷合金牌号为3003，来料宽度有2种1 395 mm和1 100 mm，最大轧制力500 t，最高轧制速度600 m/min，板形辊测量分区为48个，中间14个区每区宽度为52 mm，两边各17个区每区宽度26 mm。板形仪距轧辊中心线2.25 m，板形数据测量采样周期20 ms，数据传输周期25 ms，预测数据和实测数据滞后时间为

27 ms,300 m/min}

为准确验证灰色预测和滚动优化的预测结果，分别采集了2种1 395 mm和1 100 mm宽度在高中低不同速度下进行预测结果仿真比对，其中一组检测值如表1中T时刻板形实测值所示。

使用灰度预测模型对板形预测值和经滚动优化后的预测值进行仿真，结果见表1中灰度预测值和灰度预测优化值。

表1 板形实际测量值、灰色预测值及预测优化值数据

仿真结果(图5)分析：在轧机低速50 m/min带头带尾轧制时，板形实测M时刻值和灰色预测M时刻值、滚动优化后预测值之间的误差分别在17.2%和12.8%左右，中速300 m/min即升速阶段时，误差在21.3%和16.2%左右，当轧机进入稳态轧制时，两者误差都大于了50%，因此灰色预测当预测步长N=2时在低速轧制过程中的预测能力远远好于稳态轧制时的预测能力，且通过滚动优化，大大提升了灰色预测模型的预测精度，但在稳态轧制中，无论是灰色预测还是滚动优化都给预测控制带来了反作用。本文通过判断速度在T时刻内不发生变化后切入Smith预估来弥补这一缺陷，经数据仿真验证(图6)，切换Smith预估后，预测数据跟随性良好，预测误差控制在20%以内。

图5 高中低速实际测量值、灰色预测值、优化预测值曲线

图6 稳态轧制时经Smith预估后的测量值曲线

选用上述1400轧机板形控制倾斜数学模型进行预测模型PID控制器进行仿真实验，滞后时间在高中低速时分别是:

6 ms,600 m/min}

仿真闭环传递函数：

(26)

其中β=0.6；ωn=44.5，板形一次设定模型：F(x)=1.4x-0.7x7; PID控制器调节参数kp=1.8；ki=0.2当给定阶跃信号时，控制策略仿真对比结果如图7所示。

图7 2种控制策略的阶跃响应曲线

在系统稳态时，加入一个20%的随机扰动，输出变量的响应曲线仿真对比结果如图8所示。

图8 倾斜干扰后的响应曲线

从图8可以看出：灰色预测优化控制器仿真结果其超调量仅为5.2%，上升时间和调节过程大大缩短，加入随机扰动后，结果表明灰色预测优化控制器抗干扰能力强。

将灰色预测优化PID控制器应用于某1400铝板带冷轧机上进行试验轧制，合金牌号3003，轧制带宽1 080,来料厚度0.3 mm,板形控制效果如图9、图10所示。

图9 1 050 mm常规PI控制倾斜量板形控制效果曲线

图10 1 050 mm灰色优化预测PI控制倾斜量板形控制效果曲线

从仿真结果及实际轧制上可以看出，本文设计的灰色预测优化PID控制的结果比常规PID控制结果，在相同条件下，超调量减少，改善了系统的动态性能，提高了系统板形控制成品的控制精度。

6 结论

将灰色预测、滚动优化和Smith预估模型和常规的PID控制器融合，提出了一种基于灰色预测模型的板形预测优化PID控制算法，通过滚动优化策略来弥补灰色预测建模维数和预测步长大小的影响。通过某厂板形实测数据的仿真实验，能够降低维数和步长选择对数据预测带来的振荡影响，提高了预测精度；稳态轧制时切入Smith预估代替灰色预测克服板形控制机构的惯性和滞后特性，符合实际生产工艺要求，同时运算简单、直观且计算时间短，通过1400铝板带实际生产验证，能够有效提高板形控制精度，非常适用于各种轧机类型的板形实时控制。