基于犹豫模糊集的毁伤效能评估方法
邢 驰,聂光戍,唐上钦,王 芳
(1.空军工程大学 研究生院, 西安 710038;2.空军工程大学 航空工程学院, 西安 710038)
1 引言
现代化战场环境愈发的复杂,目标的毁伤评估也变得愈发困难,但其作为再次打击的有力评判依据,就必须要求选取的评估方法既高效又有依据。最近的研究中,常用的毁伤评估方法有:毁伤树法[1-2]、层次分析法[2-3]、贝叶斯网络[4-5]、模糊综合评判法[2,6]等,这些方法在不同应用场景中表现出不错的效果:李林[2]用多级模糊综合评判法对不确定环境下的战场毁伤等级进行评估,侯夷[6]也提出了一种二级模糊评判模型,但是都只考虑了参数区间值的模糊性,并没有考虑到隶属度的不确定性。吕红亮等[3]引入三角模糊数互补判断矩阵确定准则层元素的权重,建立了灰色关联层次分析法评估模型,但在多名专家共同评分系统下应用不强。本文改进了DRATSCI评估模型[7]中提到的基于模糊模式识别的等级评估方法。Alemi-Ardakani M[8]也利用了准则间相关性方法(CRITIC)对其进行改进,Yu C[9]提出了改进的熵赋权法(E-DRASTIC),Wang J[10]采用线性组合赋权法将改进的层次分析法和信息熵方法相结合,Mohammadi和Yu介绍了熵权法的应用并对连续型输入参数值进行了模糊处理[9-11]。但是这些方法没有从犹豫模糊的环境中进行评估,导致在犹豫模糊这种不确定环境下无法融合不同专家的评分,得出确定的评估结果。
针对文献[7-8]方法忽略了专家评分的不确定性,以及处理连续变量离散化的缺陷,本文引入了犹豫模糊集(HFSs),发展了一种基于犹豫模糊集的熵权模糊优化方法改进DRASTIC,以减少连续输入变量离散化和权重分配所带来的不确定性。首先,通过提取毁伤指标参数,分析各参数值的有效作战范围,利用高斯隶属度函数,使用模糊规则下的连续评分替代初始的专家评分,改进了传统单一模式的评分方案。而后用客观犹豫模糊熵权代替原始熵,提出主客观结合的复合权重,避免了主观赋权的不确定性,以及客观赋权法在低样本数据时导致参数权重与实际意义上略有差异的现象,最后通过计算不同HFSs之间的距离测度[26],求出输入样本的各个参数隶属度距离不同毁伤等级的标准参数隶属度的汉明(Hamming)和欧几里得(Euclidean)距离,从而求出输入样本与不同毁伤等级之间的隶属度。
2 犹豫模糊集及DRASTIC方法的介绍
1)犹豫模糊集(HEEs)
定义1[12-13]:设X为参考集,X上的犹豫模糊集(HFS)记为A,A是用函数hA(x)定义的,当x∈X时,返回[0,1]的子集,即:
A={
其中,hA(x)是[0,1]中的一组不同的值,表示元素x∈X对A的可能隶属度。
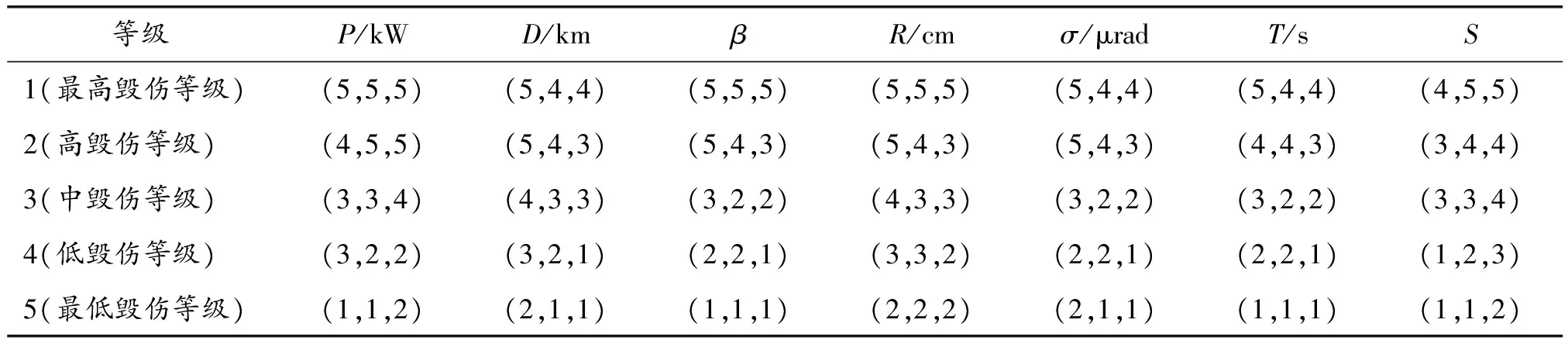
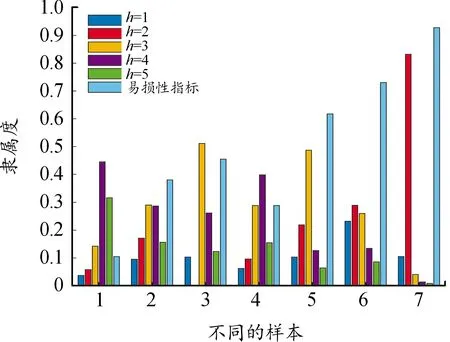
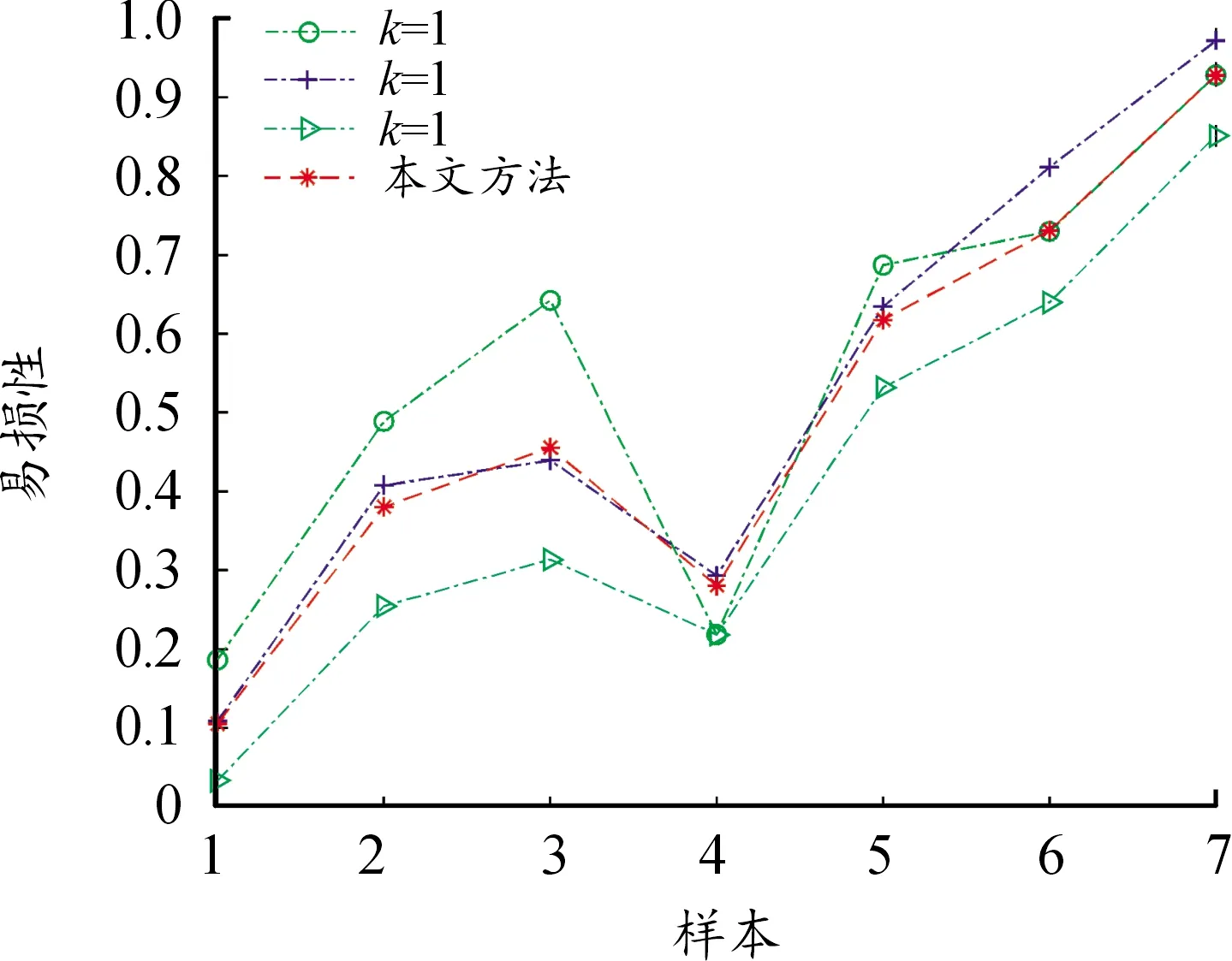
Xu Z S等[14]提出:以递减的顺序排列HFE中h的值,并且让hσ(k)(k=1,2,…,lh)表示任意两个HFEs:α和β,其中lα和lβ分别是α和β中的数值个数。当lα≠lβ,将较短的一个延长到两个HFEs具有相同的长度,并给出了如下规定:如果lα 定义2[15]:上述运算法则,设l=max{lα,lβ},Xu,Z.S.和Xia,M.M.定义了HFEs的犹豫汉明(hamming)距离和欧氏距离: (1) 当p1=1时为HFEs的汉明距离测度,当p1=2时为HFEs的欧式距离测度。 2)文献[7-8]中的DRASTIC评估方法 文献[7-8]中的DRASTIC方法主要通过一种模式识别的方法,判断输入样本参数值距离某一等级下此参数标准值的加权距离。 文献[7-8]中的评估指标评分值可以表示为[11] 其中:V为整体指标评分值,Wj为参数j的归一化理论权值,Ri为参数j的初始评分值。 由于毁伤过程中不确定因素影响较多,特别是大气传输模块中的线性效应和非线性的热晕效应。对于传输性能的影响难以用简单的数值模拟计算出来,一些学者常以概率的形式来反应这些大气效应对激光传输能力的影响,而本文的方法是通过模糊的专家评分来判断最终的毁伤等级[16-19]。本文主要根据徐国亮[20]提到的指标参数,并参考其他学者对作战参数的具体分析[21-23],主要对作战性能和参数对毁伤等级的影响作以概括。具体指标范围如下: P:激光器发射功率,0~100 kW,激光发射功率与毁伤等级之间的函数曲线呈凹性,当功率较大时功率增大越快,毁伤等级的变化越快。根据此特性,结合专家经验将输入的功率划分成不同长度的评分区间。 D:作战距离,0~5 km,作战距离与激光器发射功率相反,当距离较远时距离增加越快,毁伤等级下降越快。 β:光束质量因子,1≤β≤5,光束质量因子β定义为测量的实际光束的远场发散角与同尺度的理想光束的远场发散角之比[18],非理想的β值总是大于1,光束质量因子越小,实际发散角与理论发散角越接近,光束扩展越小,相应的毁伤能力越强。 R:远场光斑大小,R63.2%,3~10 cm,远场的功率密度呈高斯分布,距离光斑中心点越远功率密度越小,文中取距离中心63.2%的区域为有效毁伤区域。 σ:ATP跟瞄误差,0≤σ≤10 μrad,误差越小,光斑稳定性越好,所需的照射时间越短[23]。 T:辐照时间,0~5 s可调,辐照时间与毁伤等级的函数曲线呈凹性。 S:目标属性,包括光电探测器,光学系统,机翼,油箱,发动机。同等毁伤能力下不同的目标区域对应不同的毁伤等级,油箱和发动机相比探测器的破坏更具毁灭性[19]。 将每个参数都分为5个分区,每个分区对应一个专家给出的清晰的评分。具体清晰评分根据文献[20-24]分析得到,如表1所示。 表1 基于经典DRASTIC评估模型的激光武器毁伤等级评分方案 为了有效地降低输出的误差,产生一条能平滑过渡的连续的曲线,本文选取了比梯形或三角形模糊隶属度函数更具优势的高斯隶属函数[11],利用Matlab软件进行模糊分析。并假设毁伤参数是独立的,每个参数的模糊化可以分别进行。隶属度定义如下: (2) 其中:μi(x)为参数的隶属度,x为模糊输参数;ci为输入参数的高斯函数的均值,σi为输入参数的高斯函数的标准差。 基于质心加权平均法使用方程去模糊化。 其中VP(x)为输出评分值;Ri为输入参数的初始评分。 以输入参数D为例,说明高斯模糊离散化评分过程。在清晰条件下,即只有一个专家对于D的5个基集评分时,高斯隶属度函数如图1所示。 图1 参数D的高斯模糊隶属度函数曲线 各参数分区的均值、标准差、临界评分值如表2所示,在清晰条件下每个分区对应一个专家的评分,而在犹豫模糊条件下每个分区对应l个专家评分,如果某个参数分区的评分数小于l,即有一个专家没有评分,则按照定义1增加其他专家对此分区的评分最小值来扩展。 表2 参数各分区的均值、标准差临界评分值 犹豫模糊集(HFEs)的应用能有效的减小决策者的主观因素对评估结果带来的影响,同时犹豫模糊评估的使用使决策和评估系统的信息更丰富判断更加可靠。犹豫模糊集的长度(l=max{lα,lβ})为3,于是对传统的清晰评估方案作以改进(表3)。 表3 改进的模糊加权评分方案 (3) (4) 参数j的模糊平均熵为 (5) (6) 因此可以得出犹豫模糊条件下的新权重计算方法,参数的修正权重是经典权重及其熵权重的线性组合: (7) ε为线性组合系数,wj归一后的权重向量表示为 W=(w1,w2,…,wm)T (8) (i=1,2,…,n;j=1,2,…,m;k=1,2,3) 评分值越高表示:此样本i中参数j的取值,对毁伤能力的贡献越高。由于每个专家对同一个参数的打分范围的总和可能是不同的,于是将评分等级矩阵X归一化如下: 对于第1个专家: (9) 当不清楚不同等级下各参数的标准值时,假设ui为输入样本对最高毁伤等级的隶属度,ui越大表示此样本的易损性越高,相对应的表示为易损性的广义加权模糊距离。 清晰条件下样本(分区)i到最高毁伤等级的距离可以描述为[7] 根据式(3)~式(7)可得,则根据式(1)可以求出犹豫模糊条件下的易损性广义加权距离: (10) 类似的可以解释为可靠性的广义加权模糊距离为 (11) 其中:p1为HFEs的犹豫距离的距离参数,p2为广义加权距离的距离参数,p1,p2=1和p1,p2=2分别代表汉明距离和欧几里德距离。最终可以通过优化目标函数F(ui)来求得最优解ui: (12) (13) 表4 分割排序产生的标准等级评分 对于lα≠lβ的情况按照Xu Z S等[15]提出的方法,增加长度小的模糊数中的最小值来扩展,使两者长度相同。 (14) 于是可得标准犹豫隶属度矩阵: 犹豫模糊条件下样本到等级的距离可以描述为 从模糊集理论的观点来看,uh,i可以认为是距离dhi的一个权重,因此综合加权距离可以更好地表达样本i和h等级之间的差异,Dhi=uhidhi。 与式(11)相似为了求解uh,i,建立了以下目标函数: 导出以下拉格朗日函数: 其中λi是拉格朗日乘数,将拉格朗日函数关于每个uh,i和λi的偏导数分别设置为零,即: ∂L(uh,i,λi)/∂uh,i=0, ∂L(uh,i,λi)/∂λi=0 可计算属于h级的样本i的隶属度公式为 (15) 最终可以根据样本对每个等级的隶属度,找出最接近的等级。若在无法求得Q的情况下,也可以通过计算样本对“最高毁伤等级”的隶属度u1,i,通过对比大量输入样本的u1,i,而后将u1,i排序并进行等级的划分,比较得出输入样本的等级区域。 假定有3个专家(l=3)对参数的不同等级分区评分,在此犹豫模糊环境下,输入7个样本,具体样本在不同指标参数下的值如表5所示。 表5 输入样本 对应表3可得犹豫模糊条件下的评分矩阵 由式(3)~式(5)可得,(HEEs)熵矩阵e(sij)(表6)。 表6 输入样本中参数的熵矩阵 再根据式(6)并结合理论权重可以求出各参数的客观犹豫模糊权重。 0.134 6,0.155 4,0.116 5) Wj=(0.153 8,0.153 8,0.076 9,0.115 4, 0.115 4,0.192 3,0.192 3) 由结果可以看出,功率、光斑大小、距离和辐照时间对输入样本更具有辨识度,其对毁伤等级的隶属度的离散程度更高,同时结合主观权重消除了样本数据不足对等级评估的影响,也可以避免专家在评估系统中主观标准的不同而导致评估结果不同。一般情况认定ε=0.5[10],由式(7)、式(8)可知: W=(0.165 8,0.155 7,0.086 8,0.138 5, 0.125,0.173 9,0.154 4) 图2 3种客观赋权法计算结果的直方图 表7 利用熵权法计算参数熵和客观权重 表8 参数间相关系数 表9 3种客观赋权法的计算结果 取范数p1=p2=2,根据式(10)~式(13)可以得到每个样本的易损性指标ui。根据式(15),可得到每个输入样本对不同毁伤等级的隶属度uh,i,如表10、图3所示。将本文方法与DRASTIC方法进行比较,分析3个专家系统在同一权重分配方案下对样本评价的差异,如图4所示,红色代表犹豫模糊环境下得到的综合评价,由于专家主观差异导致第1个专家和第3个专家对样本的易损性评价误差比较大。由于专家1对样本7的评价为等级为5的标准评分,以样本7为例,对比标准评分方案的结果,发现在专家3的评分基础上的得到的易损性评价误差为7.8%,专家2的误差为4.2%,而文中所提方法将误差减少为0.2%,所得结果较为接近标准等级评分。 表10 不同样本对5种毁伤等级的隶属度以及分布情况 图3 样本对不同等级的隶属度直方图 图4 样本易损性曲线 1)本文提出的方法拓展了传统的加权优化模糊识别等级评估方法的应用范围,考虑了适合处理属性决策问题模糊性和不确定性的犹豫模糊评价方法,当评价信息有几个可能值组成时,能够在充分保留原始决策信息的同时,减轻决策系统主观性的影响,保证能得到一个综合性的毁伤等级结果,所提方法将误差减少为0.2%。 2)该方法利用了犹豫模糊熵求客观权重,同时将主观和客观的权重进行线性组合,适合在犹豫环境下产生较为合理的权重分配结果。 本文提出的犹豫模糊集可以表示不同决策者的评分偏好,将犹豫模糊集扩展到区间犹豫模糊集,表示决策者不能给定一个确定的评分或者隶属度的情况。本研究存在以下不足:例如,样本数量不足,下一步还需从数据挖掘和区间犹豫模糊集的角度进行优化;高能激光武器毁伤数据的有效性有待进一步验证。3 高能激光武器毁伤原理及其毁伤指标参数的提取
3.1 评估指标参数确定
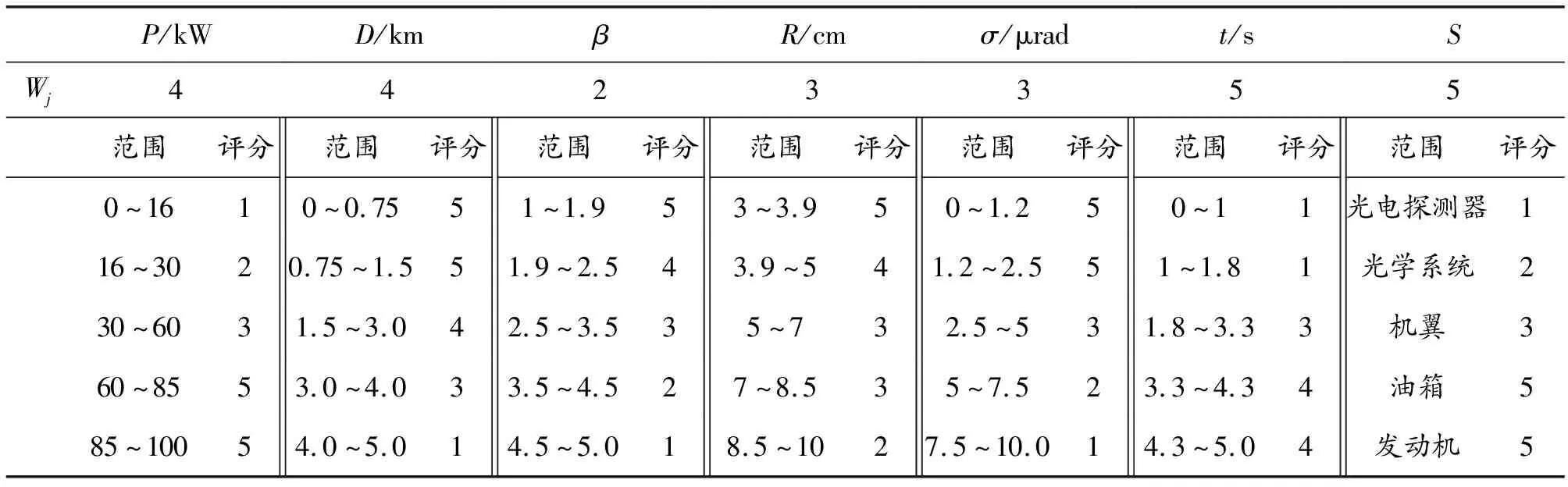
3.2 连续参数值的离散模糊与去模糊化
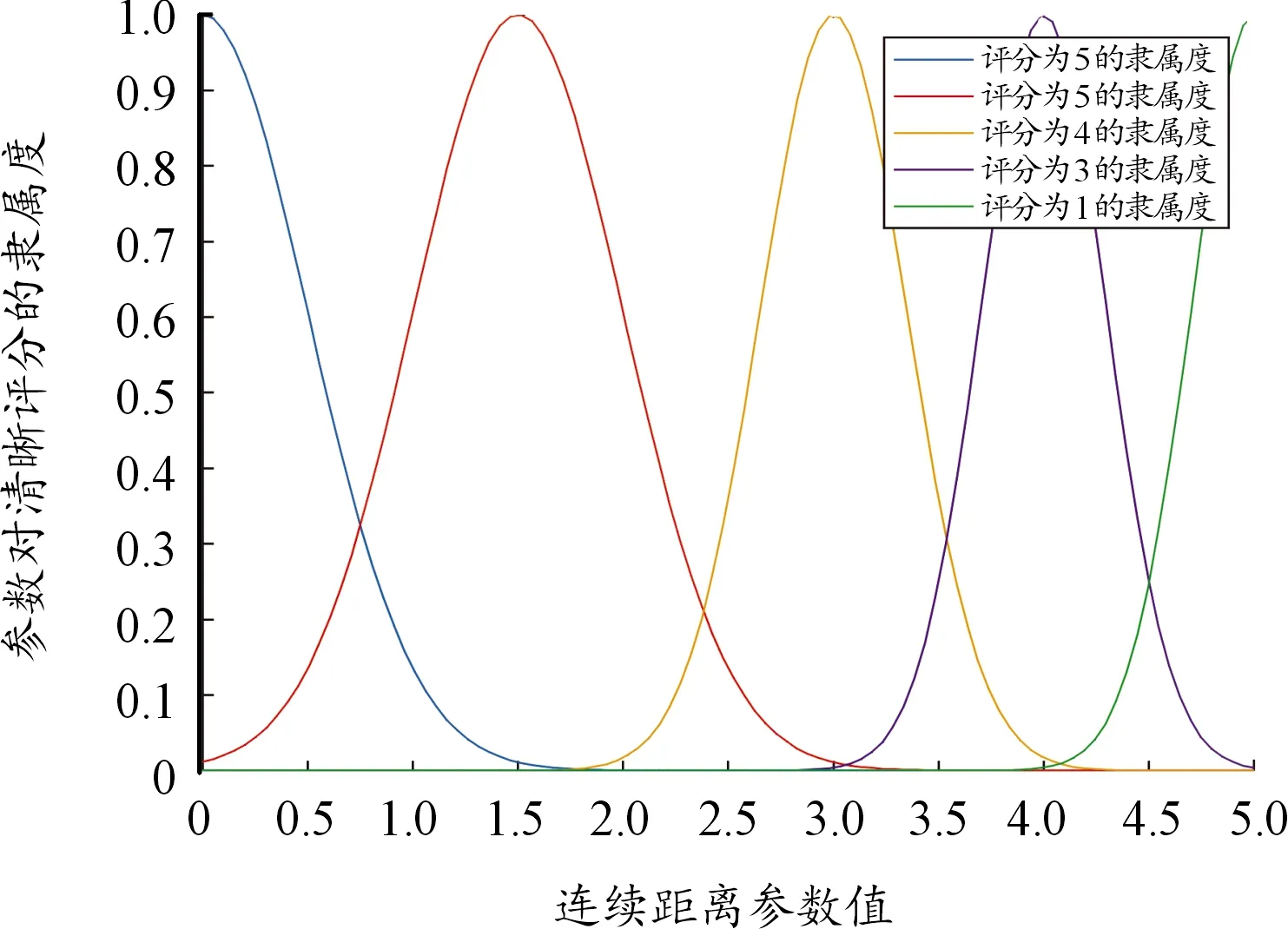
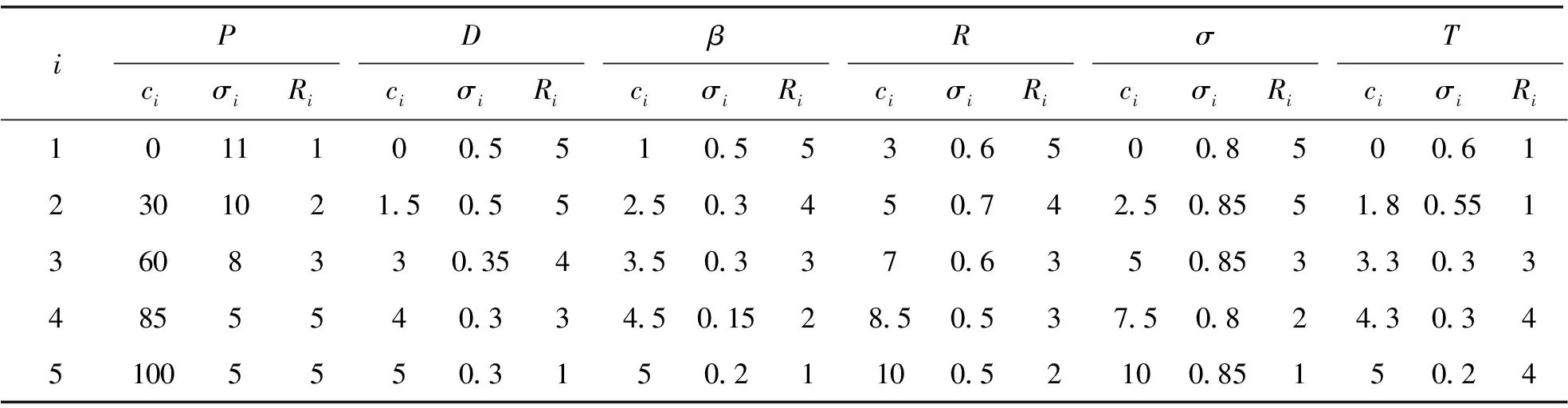
4 基于犹豫模糊集的评估方法
4.1 犹豫模糊评分矩阵
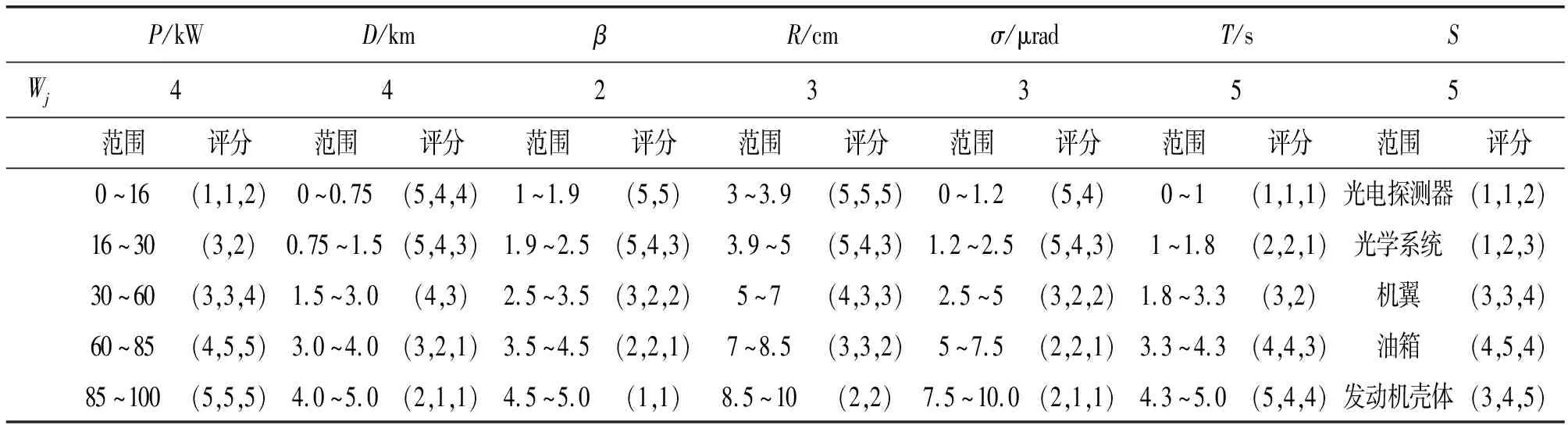
4.2 组合权重的计算

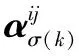
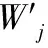
4.3 犹豫模糊集下的样本评分矩阵
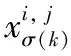
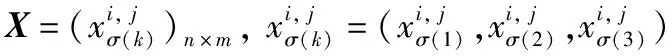
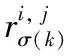
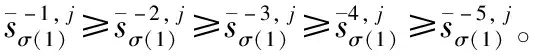
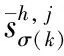
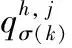
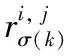
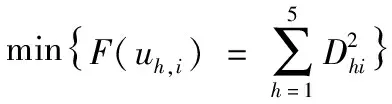
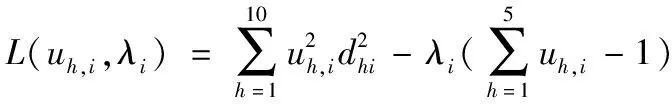
5 应用实例
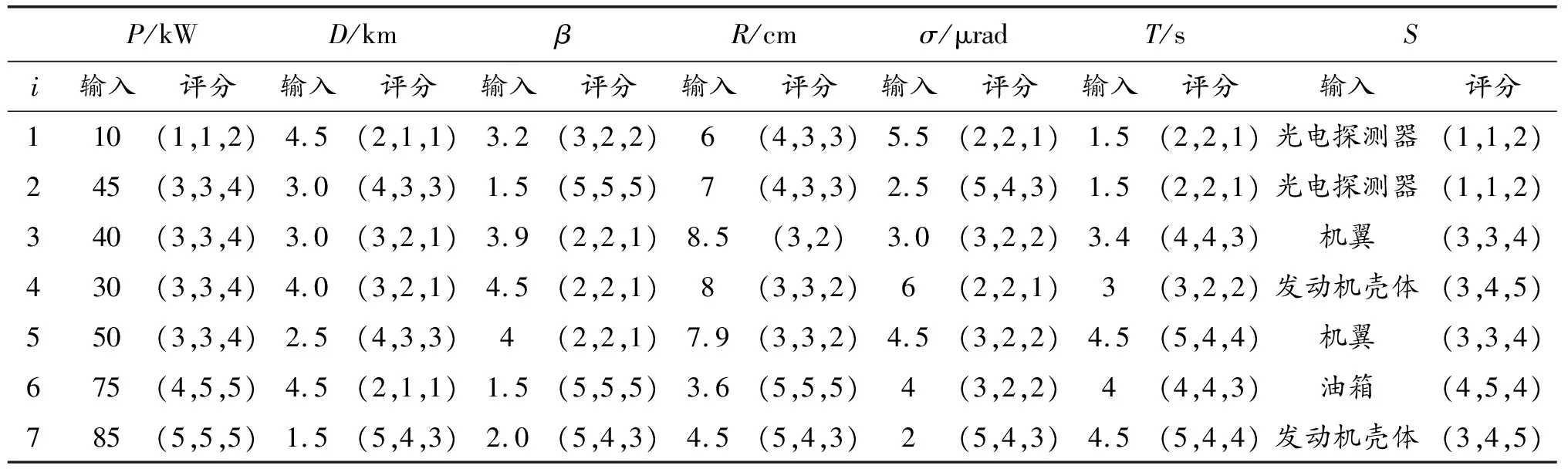
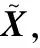
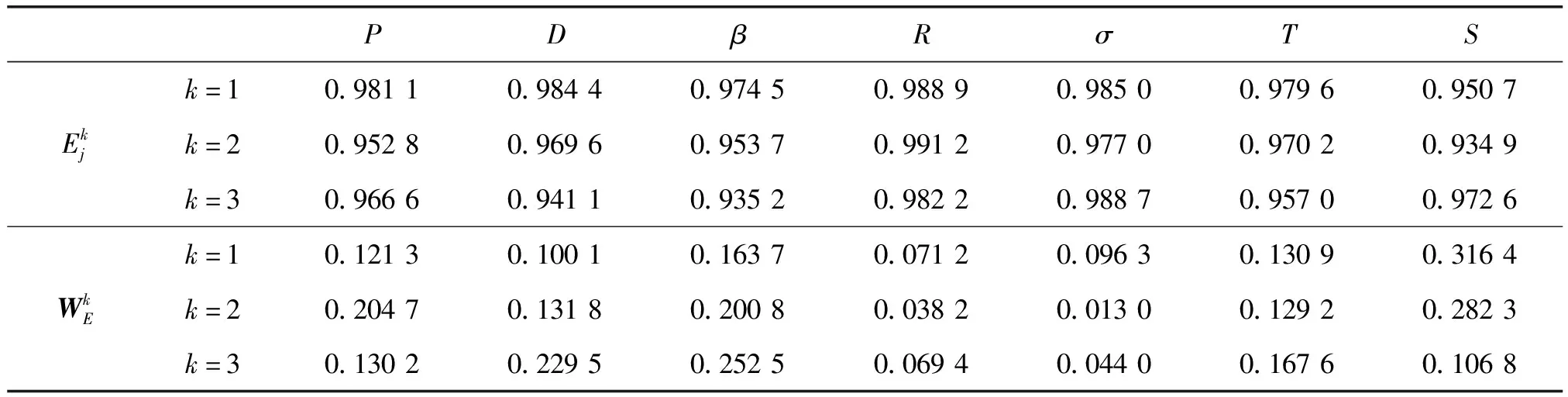
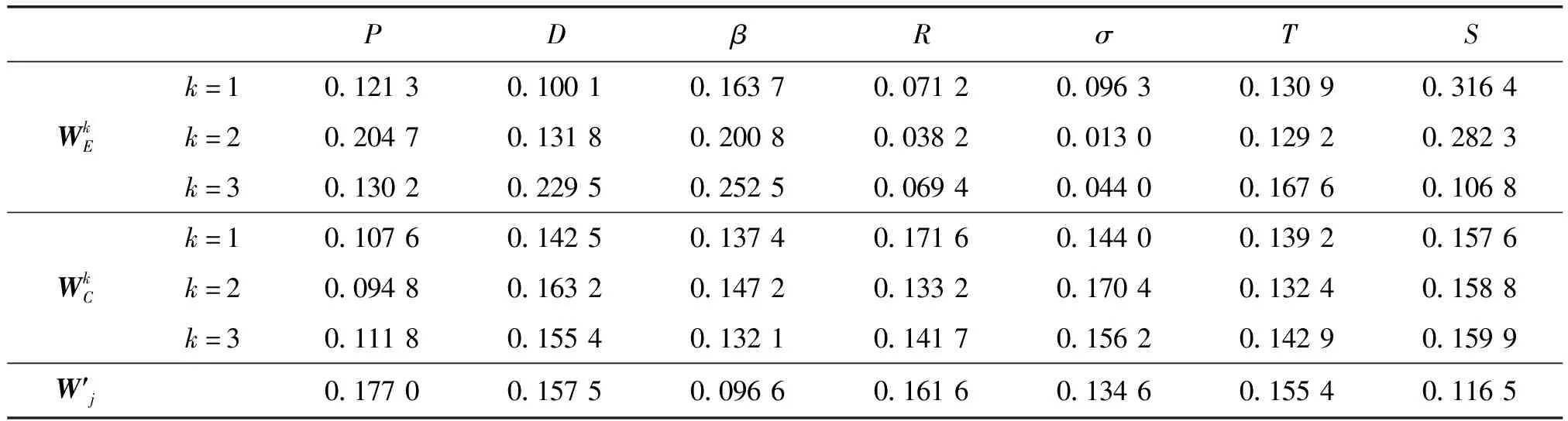
5.1 基于犹豫模糊熵的权重分配
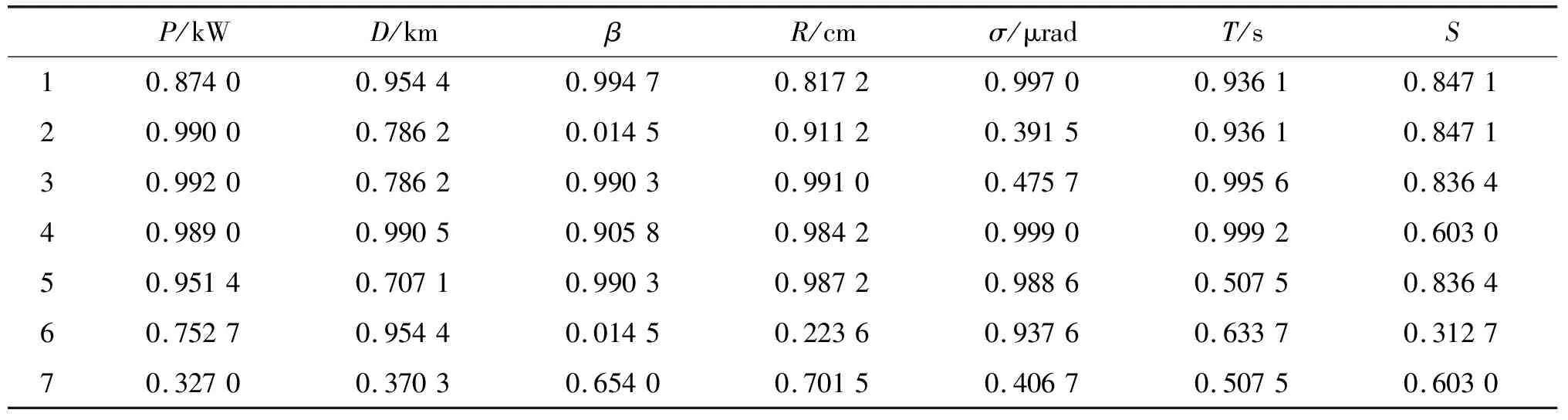
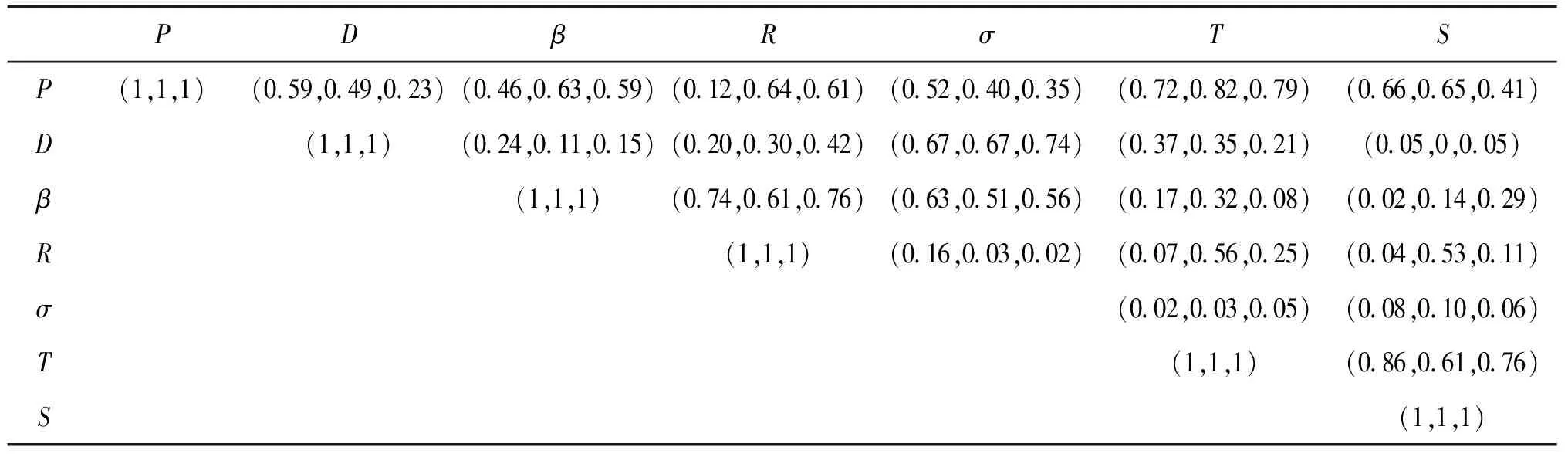
5.2 不同权重分配方法的比较
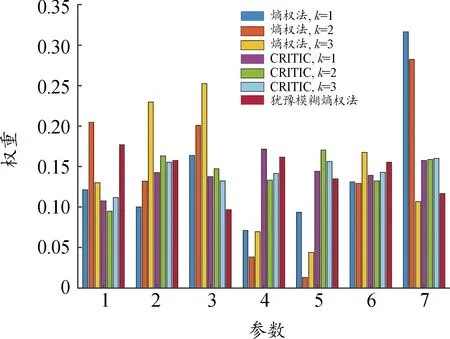
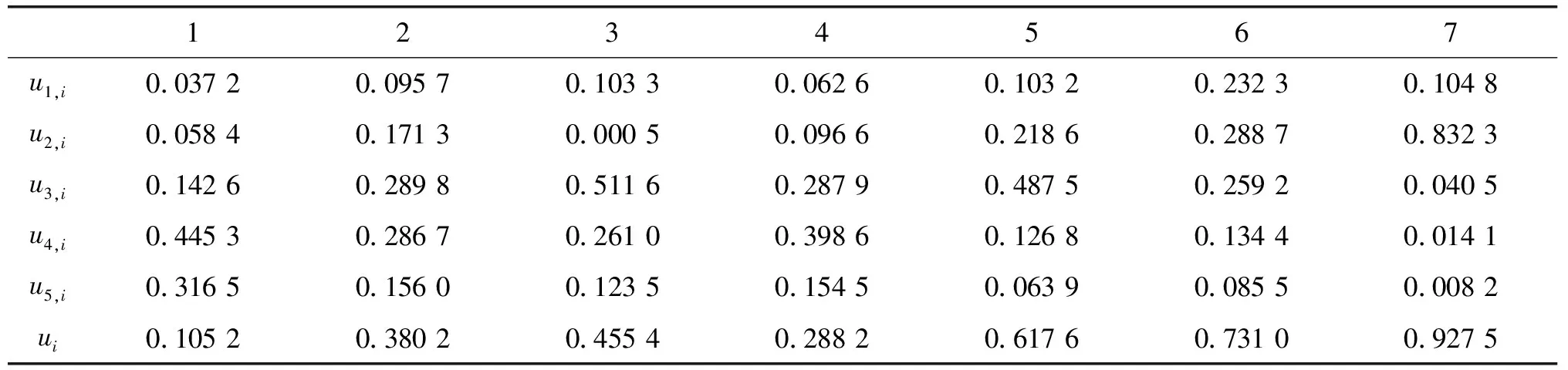
6 结论

