基于增强型果蝇算法的智能车移动路径规划

陈 中，陈克伟，张前图，刘瑶华

(1.盐城工学院 电气工程学院，江苏 盐城 224051;2.陆军装甲兵学院 兵器与控制系, 北京 100072; 3.中国人民解放军驻重庆地区第五军代室，重庆 404000)

1 引言

在智能车智能移动车辆领域，路径规划是智能车完成自主移动的首要条件，可以说是智能车的关键技术之一，一直以来都是国内外学者的研究重点[1-2]。智能车的路径规划，简而言之就是在整个运行环境内，找到一条从起点至终点的无障碍行驶路径，并满足行驶路径最短、能耗最少、耗时最短等要求。关于路径规划方法，从目前国内外已有的文献来看，主要包括传统方法和智能方法2种。传统方法主要包括人工势场法[3-4]、A*算法[5-6]等，智能方法主要是通过一些智能算法(如蚁群算法[7]、遗传算法[8]、粒子群算法[9]等)进行路径规划。和传统方法相比，智能算法的总体运算速度更快、计算效果更高，获得的移动路径更优。

虽然上述提到的智能算法在路径规划中有较好的效果，但由于算法本身存在一定的缺陷，这就导致得到的路径规划结果可能并没有达到最佳状态。因此，国内外很多学者又对这些智能算法进行改进设计，以此来进一步提升路径规划的能力。如，Zhou等[10]针对天牛须搜索算法的不足，提出基于改进天牛须搜索的智能车路径规划新方法，相比于改进前，规划得到的移动路径大幅缩短；Paikray等[11]针对粒子群算法的不足，提出正余弦粒子群算法的多机器人路径规划方法，实验结果表明正余弦粒子群算法在无碰撞路径、到达时间和能耗上均比粒子群算法更优；Guo等[12]针对地面无人车辆多目标路径全局规划问题，提出改进粒子群算法对该问题进行求解，实验结果验证了改进的有效性。

果蝇优化算法[13](fruit fly optimization algorithm，FOA)也是一种智能优化算法，同样可以应用到智能车的路径规划中。但FOA同前文所述的智能算法相似，算法本身存在易陷入局部最优[14-15]、后期搜索精度不高[16-17]等问题，如果直接将其用于智能车的路径规划中，算法本身存在的缺陷势必会对路径规划效果造成影响。因此，有必要对其缺陷进行改进设计，以达到提升智能车路径规划效果的目的。

本文以FOA为智能车路径规划方法，同时针对FOA存在的缺陷，对其进行改进，提出增强型果蝇算法(enhanced fruit fly optimization algorithm，EFOA)，以得到提高智能车路径规划效果的目的。3个典型函数的测试结果和3种不同行驶环境的智能车路径规划实例验证了EFOA算法的有效性。

2 智能车路径规划模型

利用智能算法进行路径规划主要包括两部分。首先，是进行环境建模，在几何法、单元分解法、可视图法、栅格法等几种常用的环境建模方法中，栅格法的操作最为简单，更适用于智能车行驶环境建模；其次，是在环境模型的基础上，利用智能算法反复迭代以找到一条最优的移动路径。

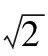
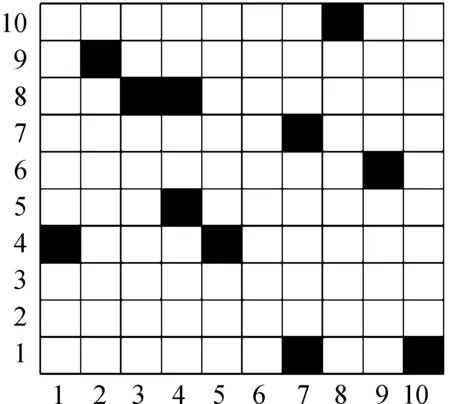
图1 10×10栅格地图

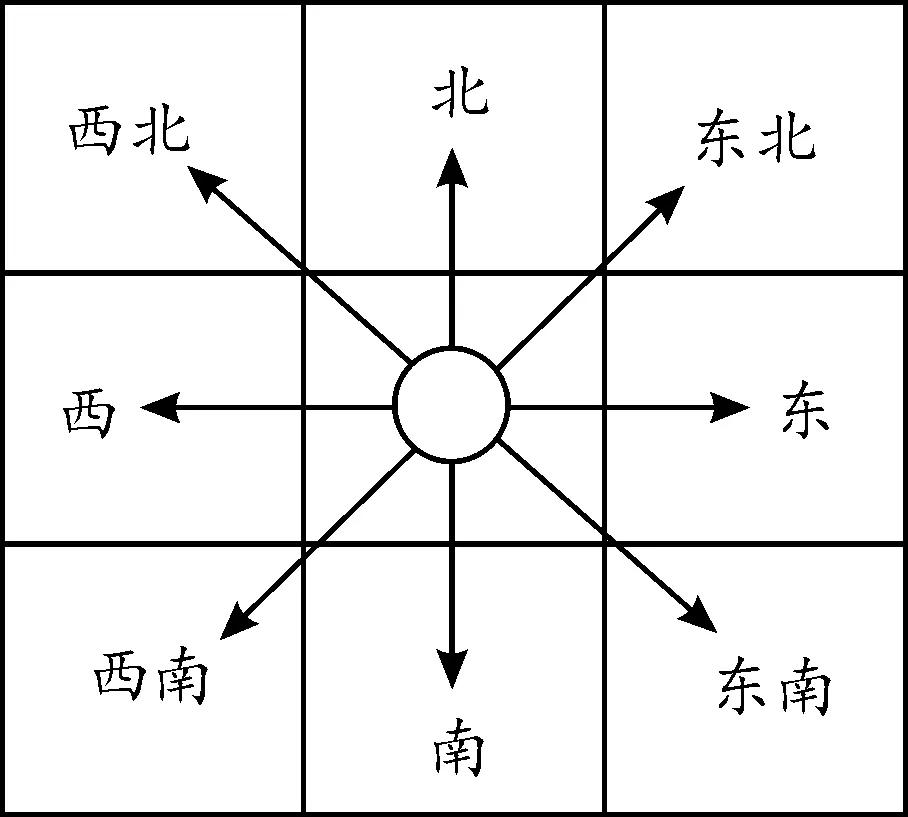
图2 8个移动方向示意图

在完成环境建模后，就可以利用智能算法进行路径规划。而对于智能算法而言，需要建立一个目标函数来评价规划路径的好坏。目标函数可以是满足路径最短、能耗最少、行驶时间最短等单个目标，也可以是多个目标的组合。目标函数可以表示为

minf(p),p∈Γ(ps,pt)

(1)

其中，f(p)为与路径相关的目标函数；p表示路径；ps和pt分别表示路径的起点和终点；Γ(ps,pt)表示从起点ps至终点pt所有可行路径的集合。在本文的研究中，将路径最短设定为目标来进行路径的规划。

3 增强型果蝇算法

3.1 果蝇算法

众所周知，FOA是模仿自然界中果蝇的觅食行为而提出的一种新型仿生优化算法，它主要有如下7个步骤：

1)设置相关参数，主要包括：果蝇种群的规模M，种群的最大迭代次数Gmax、种群的初始位置X_axis和Y_axis、果蝇个体的搜索视觉长度L；2)更新果蝇个体的位置，如式(2)所示。

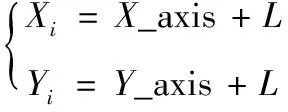
(2)

3)计算果蝇个体与坐标原点之间的距离Disti，而后将距离的倒数值Si作为发现食物的味道浓度判定值：

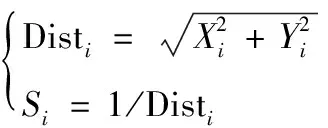
(3)

4)计算果蝇个体的食物味道浓度Smelli，即将Si代入适应度函数(在智能车的路径规划中，适应度函数可以为路径最短、能耗最少等，通常以实际需要进行设定)得到Smelli。

Smelli=function(Si)

(4)

5)对于当次迭代，通过式(5)对种群中Smelli值最大的果蝇个体的位置信息和食物味道浓度信息进行保留；

[bestSmell,bestindex]=max(Smelli)

(5)

6)在将当次迭代中bestSmell值记录到数组Smellbest中的同时，所有果蝇个体均移动至bestSmell值最大的果蝇个体处；

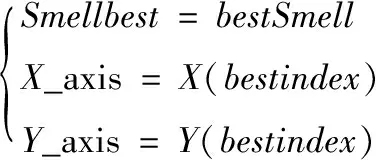
(6)

7)继续迭代，重复执行上述步骤2)～步骤6)，并判断当次迭代所得bestSmell是否比前一次迭代更优，如是，则将其记录至Smellbest中；反之，则仍将上次迭代所得bestSmell记录至Smellbest。当迭代次数达到Gmax，则停止迭代，输出最优结果。

3.2 增强型果蝇算法

从上述FOA的基本步骤中可知，当算法的步骤5)执行完毕后，当次迭代中最优果蝇个体位置信息得到了记录。以此位置为基础，在步骤6)中，所有的果蝇个体都会移动到该位置，即果蝇种群从分散的位置完成了聚集，并随后以这个聚集的位置为中心，通过搜索视觉长度L向四周进行搜索。但是，如果当次迭代中搜索到的位置是局部最优位置且L设置得不合理时，则果蝇种群在该位置聚集后，就极有可能陷入局部最优而无法跳出，不能在更广阔的空间进行搜索，从而降低算法的寻优精度。

因此，本文为克服FOA中存在的上述不足，对果蝇个体的位置更新方式进行改进，即在寻找到当次迭代中最优果蝇个体所在的位置后，其余果蝇个体并不是直接聚集到该位置，而是缓慢的向当次迭代中最优个体所在的位置靠近，改进后的果蝇个体位置更新方式如式(7)所示。

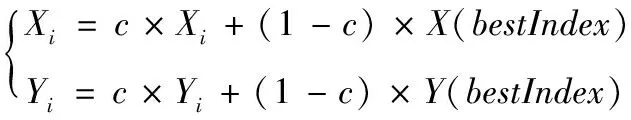
(7)

其中，c为一个0～1之间的随机数。式(7)实现了式(2)和式(6)的部分融合，通过这一改进，果蝇个体就不再单纯的向当次迭代中的最优位置聚集，而是缓慢的向其靠近。并且，整个迭代过程都不再受L设置是否合理的影响。同时，由于c为一个0～1之间的随机数，且每次迭代所得最优位置往往都是不同的，这使得果蝇个体每次移动的步长和方向是不同的，果蝇个体搜索的随机性和广泛性就得到了保证，从而避免算法陷入局部最优后无法跳出。

3.3 EFOA测试

为了验证对FOA改进的有效性，本文利用1个单峰值Sphere函数、1个多峰值Griewank函数和1个无限震荡Scahffer函数对FOA和EFOA的性能进行对比分析，上述3个函数的表达式依次如式(8)、式(9)和式(10)所示。其中，3个函数的搜索范围依次为[-100,100]、[-600,600]和[-100,100]；3个函数的维数依次为30、30和2；3个函数的理论极值依次为0、0和-1。

(8)

(9)

(10)

在计算开始前，设置FOA和EFOA的最大迭代次数Gmax均为2 000，设置果蝇种群规模M均为40。依次采用FOA和EFOA对3个函数进行20次理论极值的搜索，得到如表1所示的测试结果。其中，最优值表示20次中搜索到的最优结果；最差值为20次中搜索到的最差结果；平均值为20次搜索结果的平均值；标准差为20次搜索结果的标准差。图3给出了2种方法得到的3个函数的寻优迭代曲线(为便于展示，纵坐标取以10为底的对数)。

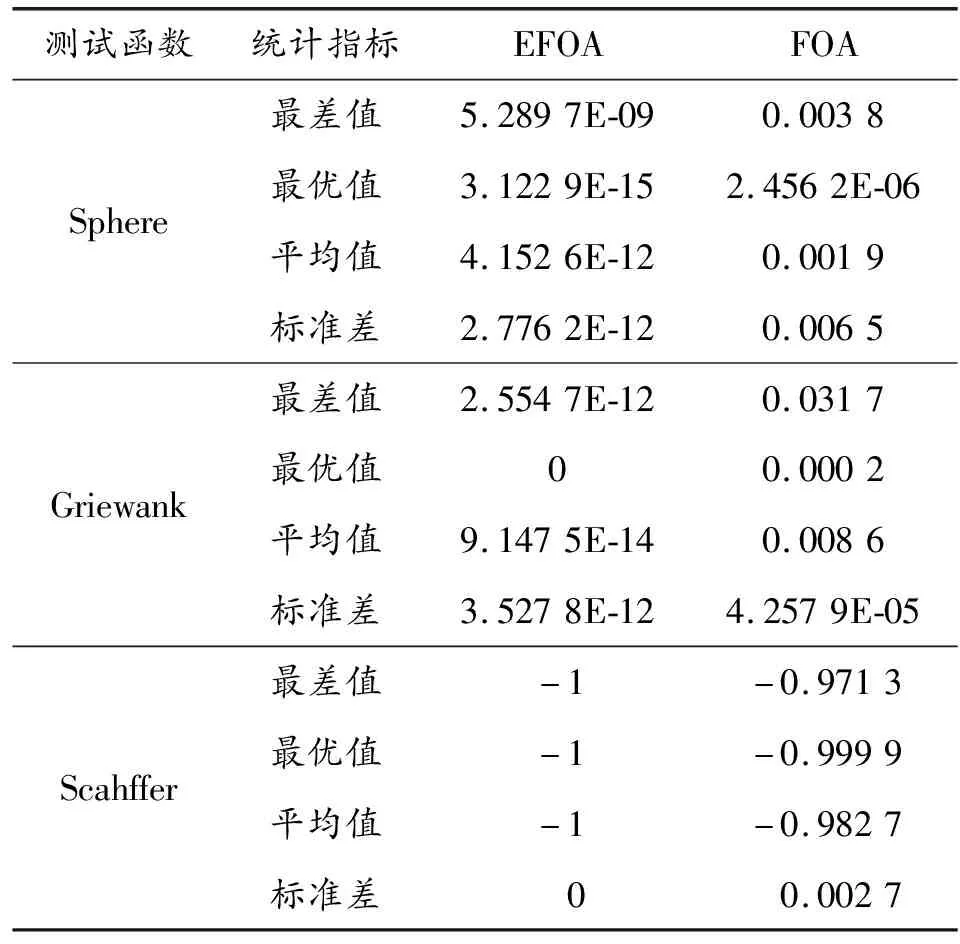
表1 测试结果

从表1可知，对于3个不同类型的测试函数而言，EFOA得到4个指标均比FOA好，如EFOA求得的Sphere函数最差值比FOA求得的最优值都还高3个数量级；又如EFOA在20次计算中部分搜索到了Griewank函数理论极值0，而FOA一次也没有；再如EFOA在20次计算中都搜索到了Scahffer函数的理论极值-1，而FOA同样是一次也没有。从图3可知，对于3个测试函数而言，FOA在搜索前期就陷入了局部最优，换言之就是迭代曲线在开始稍有下探后就保持不变了，而EFOA在整个搜索过程中迭代曲线却是在不断的往下探。表1和图3的结果表明，无论是在搜索精度、搜索速度和搜索稳定性方面，EFOA均是要强于FOA。

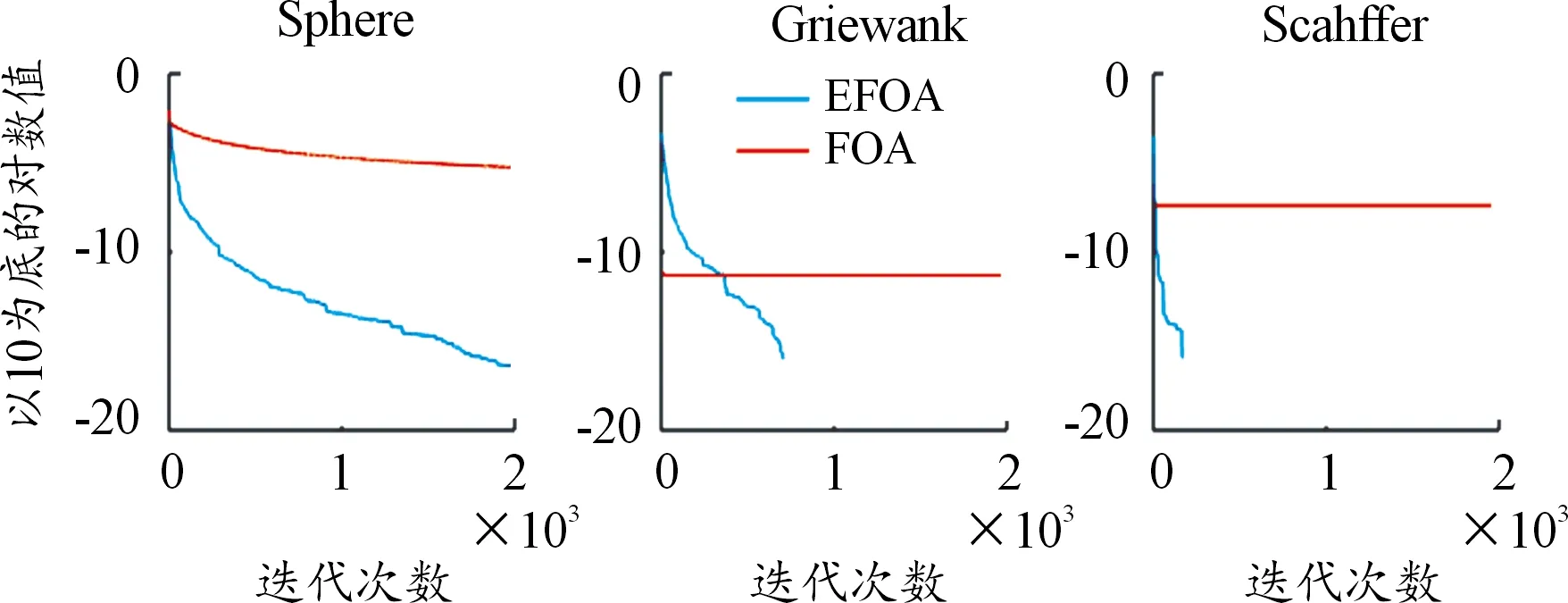
图3 3个函数的迭代曲线

4 路径规划应用

本文在MATLAB环境中分别构建简易地图(20×20栅格地图)和复杂地图(40×40栅格地图)用于分别模拟智能车在简易空间和较复杂空间的路径规划。同时，本文还采用自主搭建的智能车系统进行路径规划实验验证。为验证EFOA在智能车路径规划中的效果，本文还将EFOA与FOA、文献[15]中的LFOA方法、文献[17]中的RCFOA方法进行对比分析。其中，LFOA和RCFOA是2种与本文EFOA不同的改进型FOA算法。在利用上述方法进行路径规划时，最大迭代次数Gmax和果蝇种群规模M分别设置为200和30，LFOA和RCFOA方法所需参数均按照原文献进行设置。

4.1 20×20栅格地图

利用EFOA、FOA、LFOA和RCFOA分别在简易20×20栅格地图中进行智能车的移动路径规划。分别得到如图4所示的路径规划结果图、如图5所示的搜索过程迭代曲线、如表2所示的计算结果。由图4、图5和表2可知，对于最短路径而言，EFOA得到了4种方法中最短路径27.77，比LFOA、RCFOA和FOA得到的路径分别缩短了2.01%、6.78%和13.14%；对于达到最短路径所需的最佳迭代次数而言，EFOA所需的次数和LFOA一样，均为11次就搜索到了最短路径，相比于FOA和RCFOA的13次和16次，分别减少了2次和5次，这说明EFOA和LFOA可以更快的搜索到最优解；对于运行时间而言，EFOA的耗时最短，比LFOA、RCFOA和FOA的耗时同比缩短了19.79%、18.48%和18.60%。需要说明的是，虽然EFOA和LFOA搜索到最优解所需的迭代次数相同，但由于LFOA算法在FOA的基础上增加了种群划分和Levy飞行步长的计算步骤，导致算法的复杂度有所增加，因此在耗时上就出现了差异。

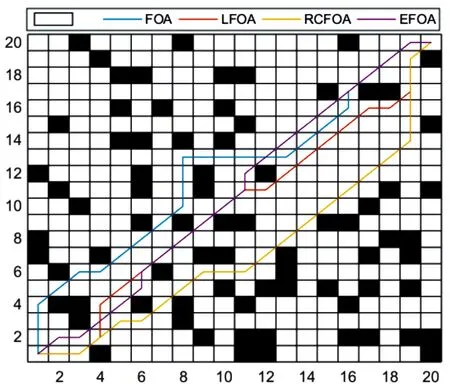
图4 20×20栅格路径规划结果地图

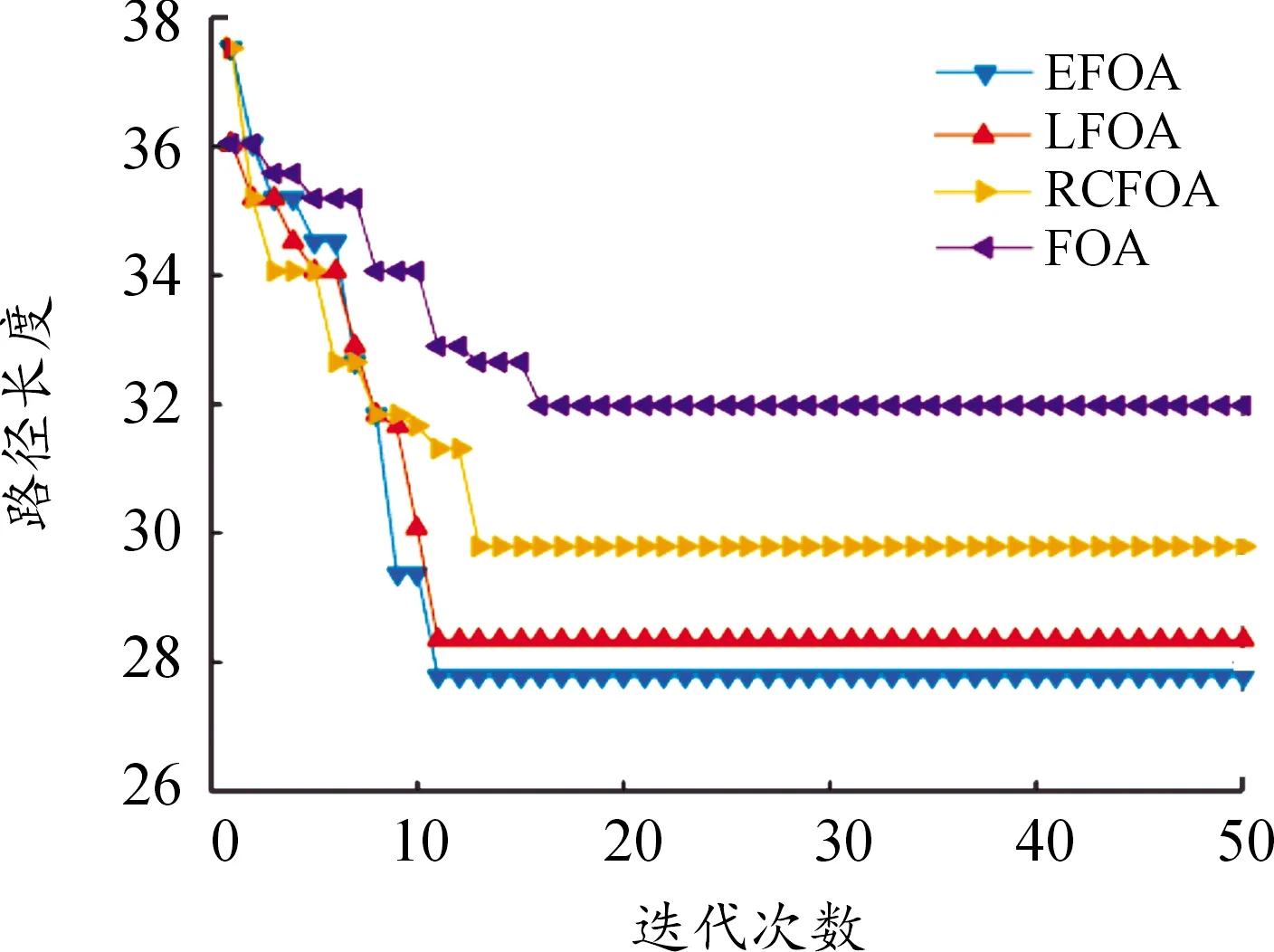
图5 20×20栅格地图路径规划迭代曲线

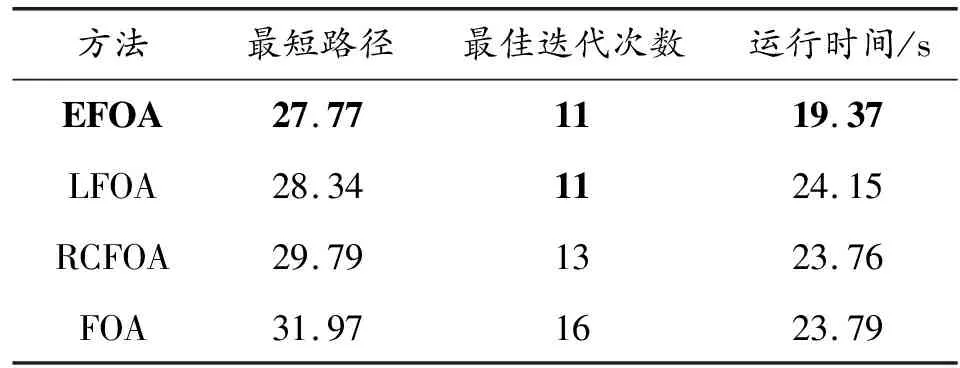
表2 20×20栅格地图各算法计算结果

4.2 40×40栅格地图

利用EFOA、FOA、LFOA和RCFOA分别在复杂40×40栅格地图中进行智能车的移动路径规划。分别得到如图6所示的路径规划结果图、如图7所示的搜索过程迭代曲线、如表3所示的计算结果。由图6、图7和表3可知，对于最短路径而言，EFOA得到了4种方法中最短路径56.86，比LFOA、RCFOA和FOA得到的路径分别缩短了4.4%、9.18%和10.23%；对于达到最短路径所需的最佳迭代次数而言，EFOA所需的次数为17次，比LFOA的16次多了一次，比FOA和RCFOA分别减少了6次和14次；对于运行时间而言，EFOA是最少的，比其余3种方法中耗时最短的RCFOA都还节省了约10 s。需要说明的是，虽然LFOA在迭代次数上比EFOA少1次，但是由于LFOA算法的复杂度要比EFOA强，因此在时间消耗上比EFOA要多。上述分析表明，EFOA在处理较为复杂环境的路径规划时，效果同样明显。

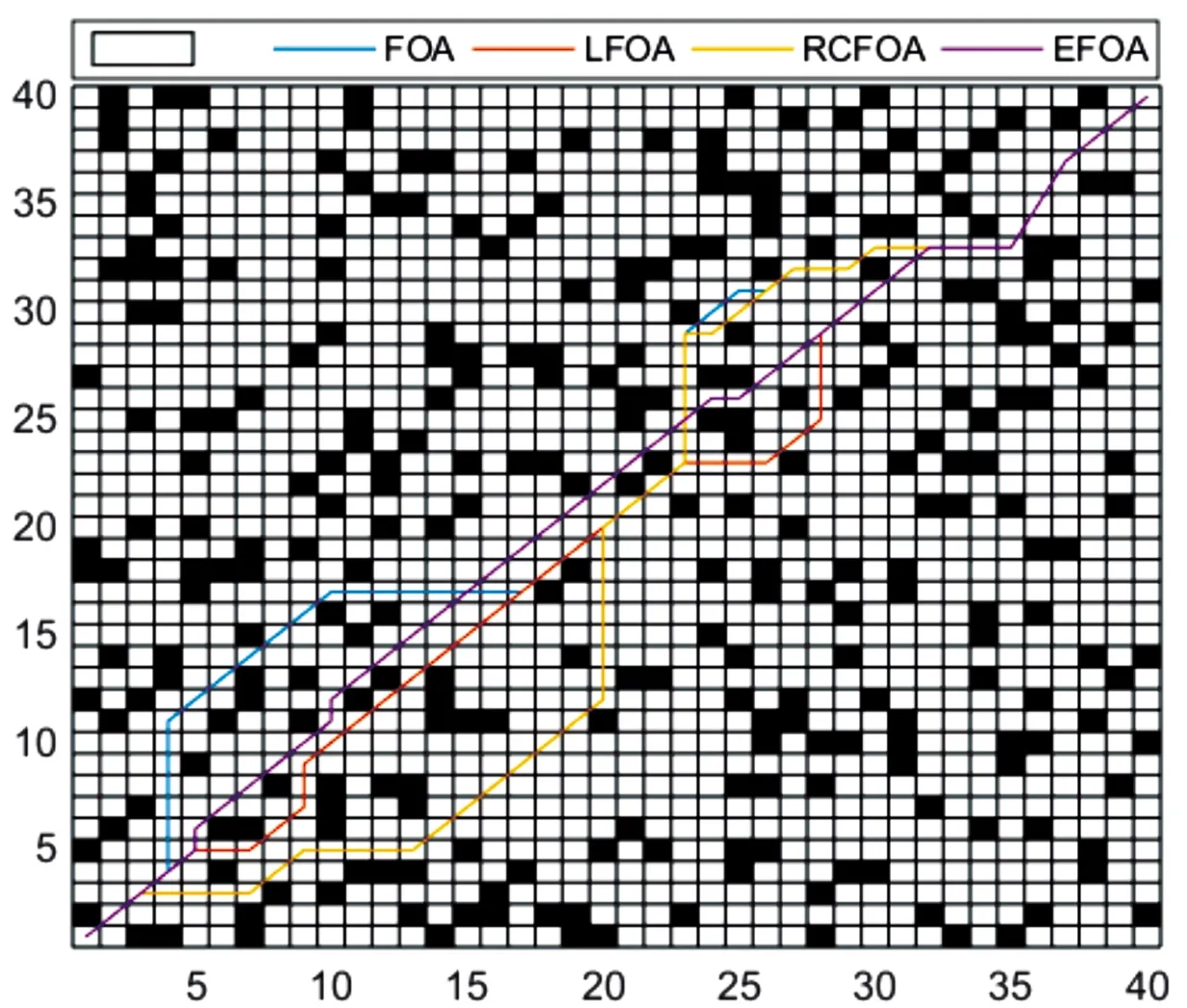
图6 40×40栅格路径规划结果地图

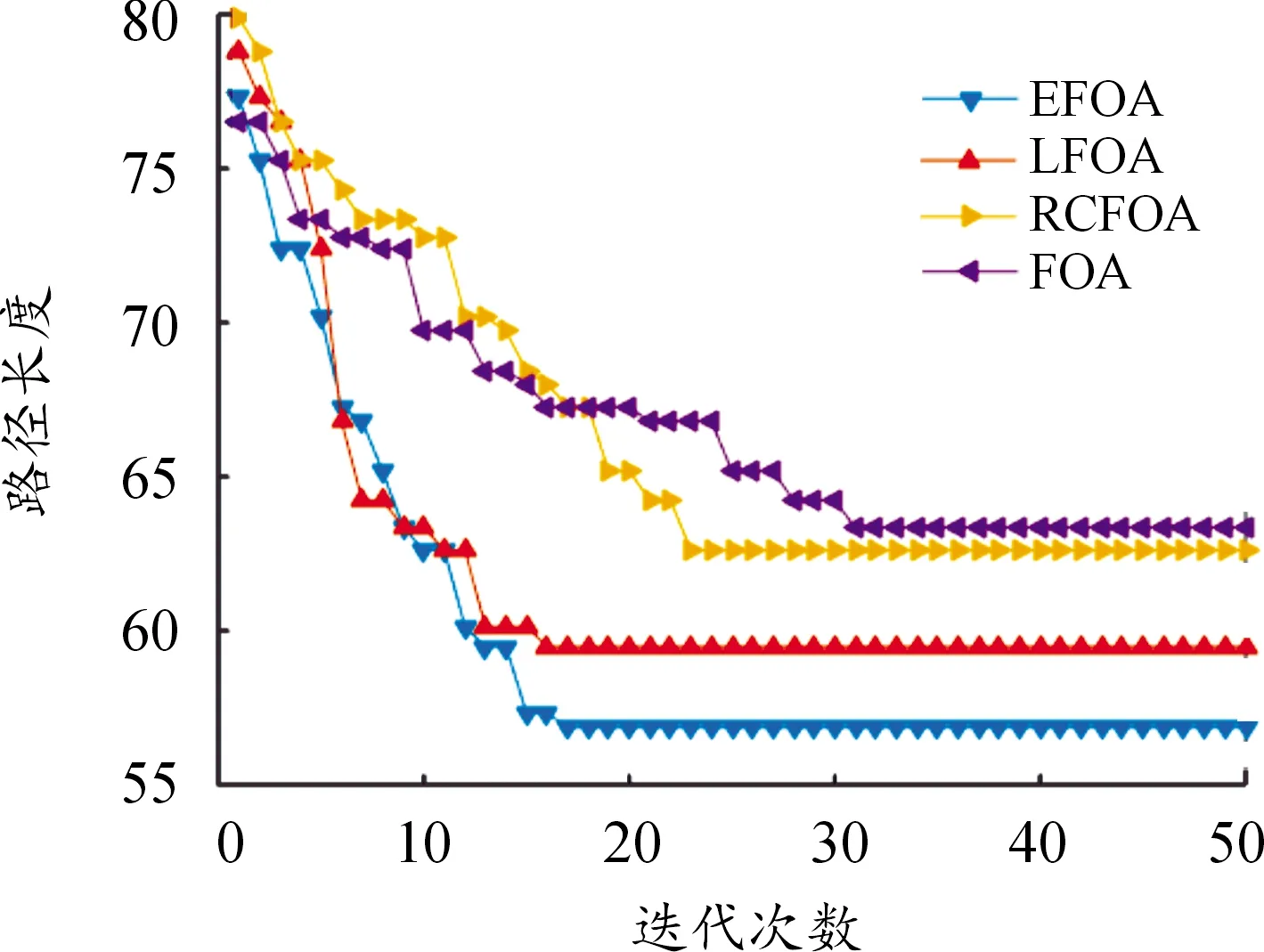
图7 40×40栅格地图路径规划迭代曲线

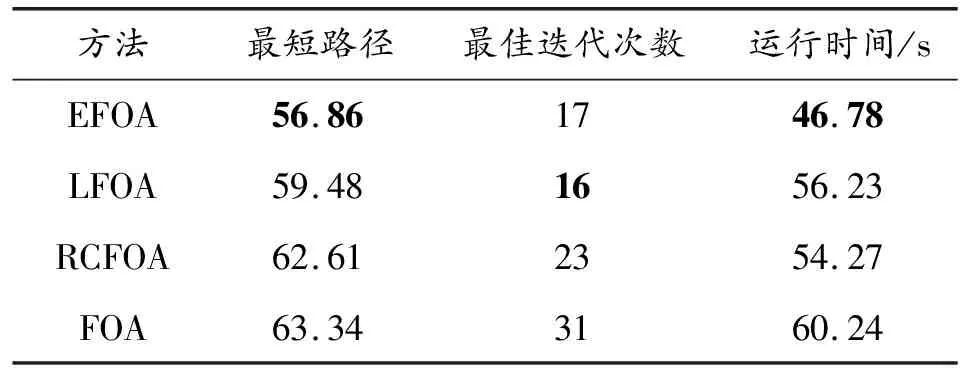
表3 40×40栅格地图各算法计算结果

4.3 实验

在利用模拟仿真进行智能车移动路径规划的基础上，本文还利用搭建的智能车系统在真实的环境中进行移动路径的规划，如图8所示。其中，图8(a)为智能车起点位置示意图，图8(b)为智能车运行过程示意图，图中的实验场景为20×20栅格。

图8 实验环境示意图

EFOA、FOA、LFOA和RCFOA等4种方法得到的计算结果如表4所示。从表4中的数据可知，EFOA得到的路径是4种方法中最短的，且耗时最少。这一结果表明本文的EFOA方法在智能车路径规划实际应用中可以以更快的速度找到更优的移动路径，可有效提高路径规划的效率。

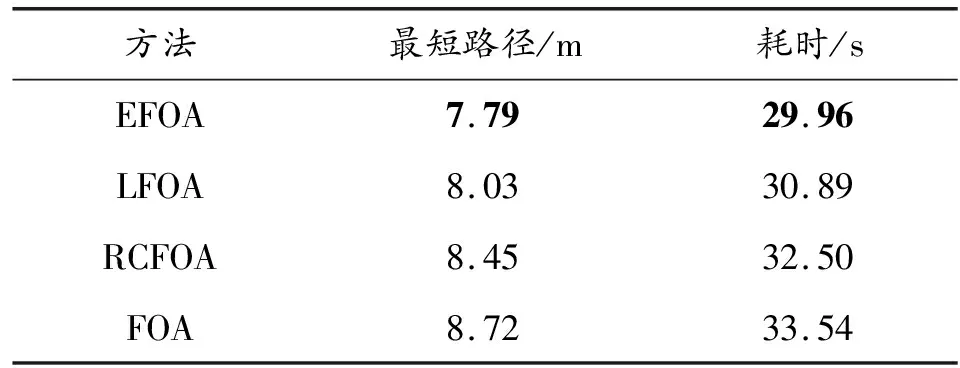
表4 真实环境计算结果

5 结论

为有效提升智能车的路径规划效果，提出了EFOA算法并通过3个典型测试函数验证了方法的有效性。将EFOA用于智能车不同行驶环境的路径规划中，效果更优。