SO（3）上航天器自适应反步姿态跟踪控制

史忠军，邵长宝，张剑桥，赵艳彬

（1.上海航天技术研究院，上海 201109；2.上海卫星工程研究所，上海 201109；3.上海航天技术研究院 北京研发中心，北京 100081）

0 引言

航天器姿态控制是实现编队飞行、交会对接、卫星通信、高分辨率对地观测等任务的关键技术［1-4］。对于在轨运行航天器，受恶劣太空环境以及燃料消耗等因素影响，在进行航天器控制器设计时，往往需要解决转动惯量不确定性以及外部干扰等问题。此外，航天器姿态动力学的非线性特性为高精度姿态控制的实现增加了难度。因此，近年来有大量学者在考虑航天器存在转动惯量不确定性以及外部干扰情况下，采用非线性控制理论进行控制器设计，解决航天器姿态控制问题。

文献［2，5］利用反步控制理论，解决了服务航天器与非合作航天器构成的组合体航天器的姿态稳定控制问题。LIU 等［6］通过设计H∞控制器解决了柔性航天器姿态稳定控制和振动抑制问题。XIAO 等［7］利用滑模控制理论设计控制器，解决了航天器姿态跟踪和执行机构容错控制问题。其中，反步控制方法因具有针对控制器设计、对干扰的鲁棒性高等特点，在航天器控制领域被广泛应用［8］。需要指出的是，在上述文献中航天器的姿态或采用局部坐标表示，或利用四元数和修正罗德里格参数（Modified Rodriguez Parameters，MRPs）进行描述。然而，采用局部坐标或修正罗德里格参数描述航天器姿态运动时存在奇异问题，四元数则需要考虑退绕问题［1］。

由于方向余弦矩阵可以在SO（3）上全局无奇异地描述刚体姿态，因此文献［9-10］基于方向余弦矩阵描述航天器姿态来建立动力学模型，解决了姿态跟踪控制问题。但是，由于SO（3）的非线性特性，在SO（3）上直接进行控制器设计比较困难［11］。文献［11-13］通过定义一个非负定的势函数描述姿态跟踪误差，将姿态动力学修改为易于进行控制器设计的形式，解决了刚体的姿态跟踪控制问题，但设计的传统的比例-微分（PD）控制器对干扰的鲁棒性差，且响应速度慢，控制精度低。ZHANG 等［1］基于此建模和控制器设计思想，采用滑模控制理论解决了航天器姿态跟踪控制问题，但却没有考虑模型不确定性和外部干扰。

基于上述国内外研究现状介绍与分析，本文针对存在模型不确定性和外部干扰的刚体航天器姿态跟踪控制问题展开研究。首先，在系统存在模型不确定性和外部干扰情况下，通过定义姿态误差势函数，推导建立SO（3）上航天器相对姿态动力学模型；然后，设计自适应反步控制器对模型进行控制，并对系统的稳定性进行严格的数学证明；最后，通过数值仿真验证所提出的控制算法的有效性。

1 姿态动力学描述

本文研究全驱动刚性航天器的姿态跟踪控制问题。首先，为描述航天器的姿态运动，定义航天器本体坐标系Fb和地球惯性坐标系FI。FI的原点为地球质心，oxI沿着黄赤交线指向春分点，ozI轴与地球自转轴重合，oyI轴通过右手定则确定；Fb的原点为航天器质心，oxb、oyb、ozb三个坐标轴与航天器的三个惯性主轴重合。航天器的姿态记为Fb到FI的转动矩阵C∈SO(3)。SO（3）为由特殊正交矩阵构成的Lie 群，满 足：SO(3)={C∈R3×3：CTC=I3×3，det(C)=1}，其中，R为实数集合；()T为矩阵的转置；I3×3为3×3 的单位矩阵；det()为计算一个矩阵的行列式。用方向余弦矩阵描述的航天器姿态运动学和动力学方程为［1］

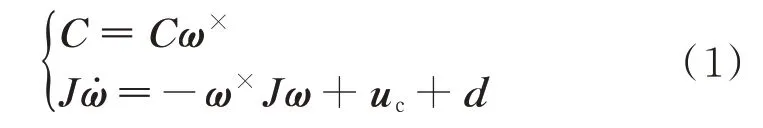
式中：ω=[ω1，ω2，ω3]T∈R3×1为本体系下航天器本体坐标系相对于惯性坐标系的姿态角速度；J∈R3×3为航天器转动惯量；uc∈R3×1为航天器执行机构产生的控制力矩；d∈R3×1为航天器所受的外部干扰力矩。

()×：R3×1→ςo(3)为计算 任意一 个三维向量x=[x1，x2，x3]T∈R3×1的反对称矩阵，具体形式为

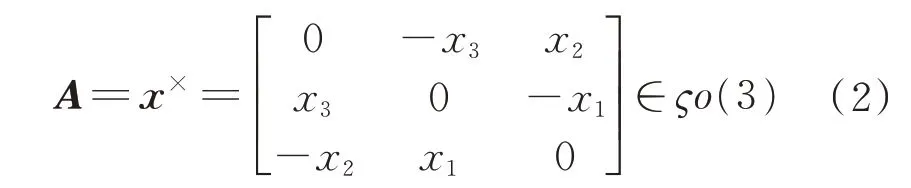
式中：ςo(3)={A∈R3×3|AT=-A}为SO（3）的李代数。

记航天器的目标姿态为Cd，且满足，其中，ωd∈C1∩L∞为航天器的目标角速度，则可以得到航天器的姿态跟踪误差和角速度跟踪误差为

对Ce和˜求导，并将式（1）代入，可以得到航天器的姿态误差运动学和动力学方程为

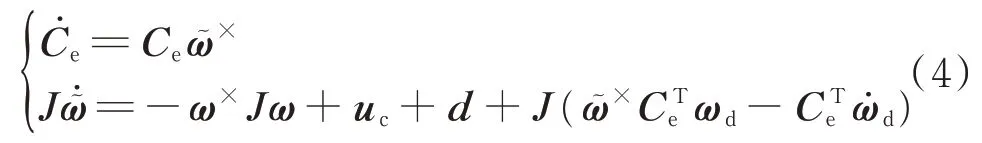
为解决航天器姿态跟踪控制问题，需要设计控制器uc，使得ω˜=0，Ce=I3×3。然而，SO（3）是一个具有9 个元素和6 个约束的非线性微分流形，姿态误差运动学中Ce的存在导致在SO（3）上直接进行控制器设计比较困难［12］。一种常用的处理方式是通过定义一个非负定的误差势函数，将Ce转化为一个三维姿态误差向量，然后对姿态误差运动学方程进行修改，再基于修正后的模型进行控制器设计。本文选用文献［13］中定义的姿态误差函数：

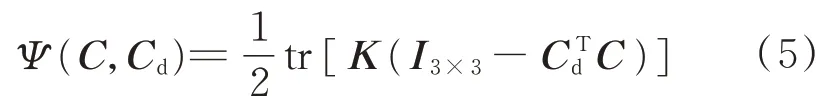
式中：K=diag(k1，k2，k3)＞0为正定对角矩阵；tr()为求矩阵的迹；姿态误差函数Ψ(C，Cd)关于C=Cd局部正定，当C=Cd时，Ψ(C，Cd)=0［13］。

对Ψ(C，Cd)取导数，有

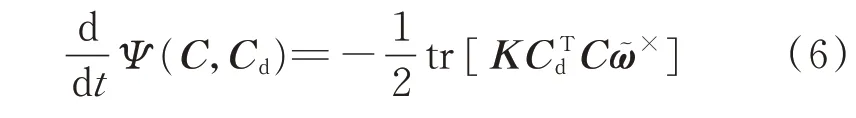
利用下述关系［14］

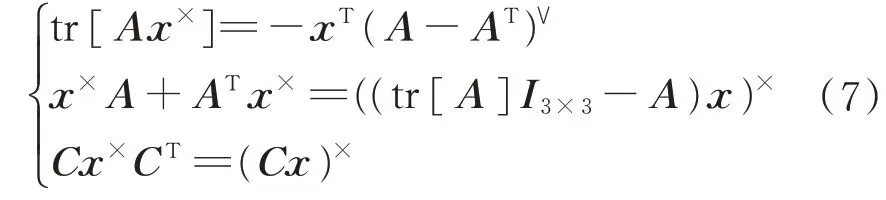
可以得到

对ec求导，可以得到修正后的姿态误差运动学方程为

则航天器姿态跟踪控制问题的动力学模型可以用式（4）和式（9）来描述。

此外，由于燃料消耗或释放载荷等因素影响，在轨运行航天器的质量和转动惯量无法精确获得。因此，需要考虑航天器转动惯量的不确定性。记航天器的实际转动惯量为

式中：J0为转动惯量的标称部分；ΔJ为转动惯量的不确定部分。

则考虑转动惯量不确定性后，姿态误差动力学方程改写为

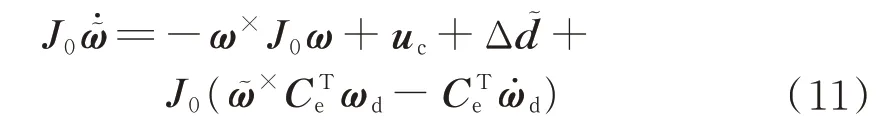
本文研究的姿态跟踪控制问题，可以由式（10）和式（11）来进行描述。控制目标：考虑外部干扰和转动惯量不确定性，在˜满足上述假设情况下，设计自适应控制器uc，使得姿态跟踪误差ec可以一致渐近收敛到零点附近的小邻域内。

2 自适应反步控制器设计

本章将通过设计自适应反步控制器来处理由外部干扰和转动惯量不确定性产生的系统总干扰，并实现控制目标。

步骤1定义下面的反步控制虚拟变量：

式中：α为虚拟控制输入。

将式（11）、式（12）和式（13）联立，可以得到构造的虚拟变量z1的动力学方程为

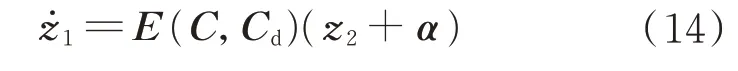
然后，选取Lyapunov 函数：

对V1求导，并将式（14）代入，可得

设计虚拟控制α为

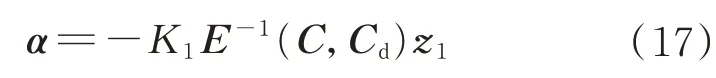
式中：K1＞0为控制器设计参数。

将式（17）代入式（16），有

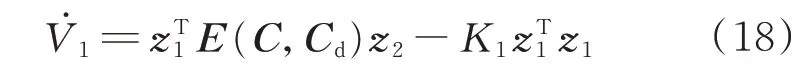
步骤2对式（13）取导数，并将式（11）代入，可以得到构造的虚拟变量z2的动力学方程为

然后，选取Lyapunov 函数

式中：γ1＞0为待设计参数为系统总干扰的估计误差为干扰的估计值。

对V2取导数，得

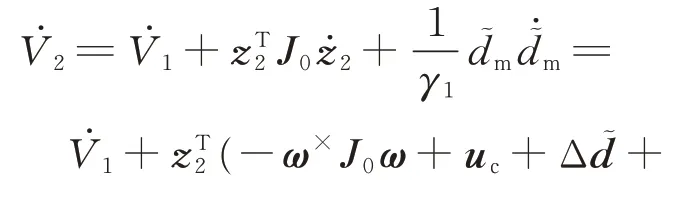
步骤3设计如下的自适应反步控制器：

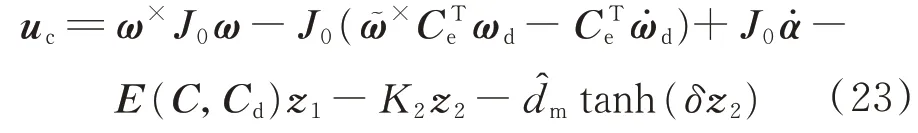
式中：K2＞0、δ＞0为控制器设计参数。

将式（23）代入式（22），得到

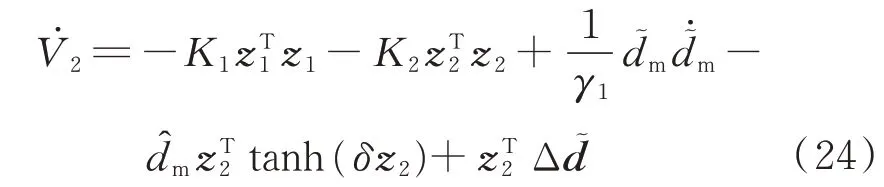
为了估计系统的总干扰dm，设计如下的自适应控制率：

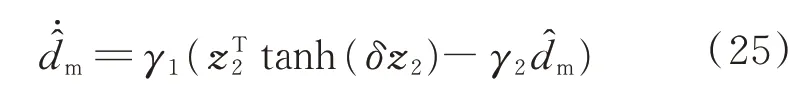
式中：γ2＞0为控制器设计参数。

将式（25）代入式（24），得到

3 控制系统稳定性分析

为了后续稳定性证明需要，首先给出下面引理。

引理1对于双曲正切函数满足下述不等式［15］：

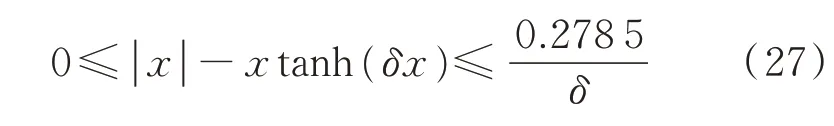
结合步骤1～3，本文研究结果可以用下述定理进行概括。

定理1考虑由式（9）和式（11）描述的航天器姿态跟踪控制系统，在满足系统所受总干扰有界假设条件下，应用控制律式（23）和自适应律式（25），航天器姿态跟踪误差ec能够一致渐近收敛到零点附近的小邻域内。

证明选取式（21）的Lyapunov 函数，经过计算后可以得到式（26）。对于项来说，满足

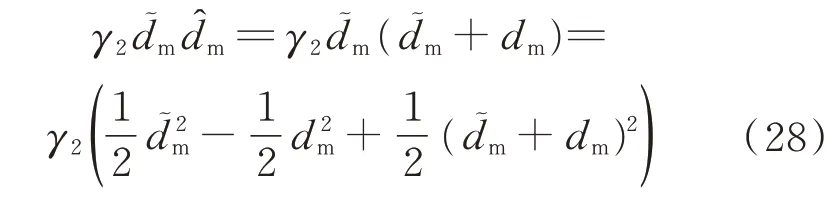
将式（28）代入式（26），并利用引理1，可以得到

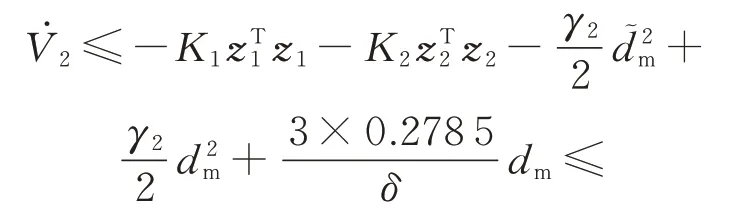
注1：对于本文研究的航天器姿态跟踪控制问题来说，最终的控制精度取决于，较小的γ2和较大的δ可以得到较小的χ。尤其是较大的δ可以明显改善系统对于干扰的鲁棒性。但同时需要注意，δ越大会导致tanh 函数越接近符号函数，会使系统产生抖振。因此，在进行控制器参数设计时，要在稳态精度和系统性能间做好平衡。

注 2：对于角速度跟踪误差来说，ω˜=z2+α，由文献［13］可知，E(C，Cd)有界。因此，根据z1、z2有界可知，角速度跟踪误差ω˜也是一致最终有界的。

注3：受航天器姿态控制执行机构的动力学特性影响，在工程应用过程中，需要考虑执行机构的输出饱和问题。因此，实际的控制输出为

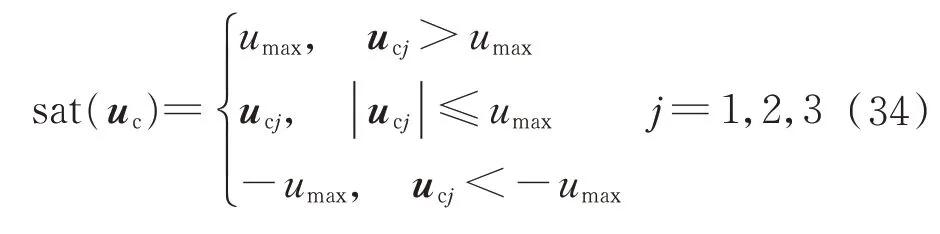
4 仿真试验及结果分析

本章将通过数值仿真分析验证本文所提出的控制方法，可以有效地解决航天器姿态跟踪控制问题。仿真过程中航天器参数如下，转动惯量标称部分为

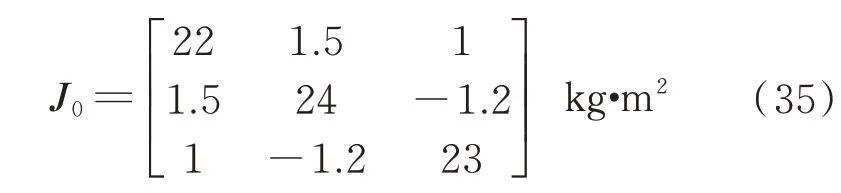
转动惯量不确定部分为ΔJ=0.15J0，航天器的控制力矩上限为umax=0.5 N·m，航天器所受的外部干扰力矩为

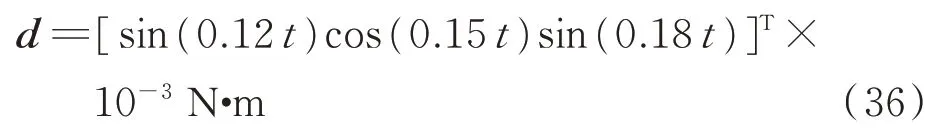
初始时刻的航天器姿态信息为：姿态转动矩阵C(t=0)=I3×3；姿态角 速度为ω(t=0)=[0.01-0.01-0.01]T×180/π((°)/s)；航天器的初始目标姿态为

为了验证本文所提出的算法的有效性，主要考虑两种情况的对比仿真。

情况1：本文所提出的自适应反步控制器式（23）、式（25），控制器参数设计为：K=diag ( [ 1 1 1 ] )；K1=10；K2=8；δ=100；γ1=0.002；γ2=0.001。

情况2：文献［12］中的类PD 控制器，用来与本文所设计的控制器的控制效果进行对比，说明本文所提控制算法的优越性，控制器参数设计为：KΩ=2.5。

情况1 仿真结果如图1～图3 所示，仿真时间设置为150 s。图1为航天器姿态跟踪误差，图2为角速度跟踪误差。图中可见，航天器姿态运动误差在30 s内收敛到稳态，通过系统状态收敛后的曲线放大图可以看出，姿态控制精度为：|eci|＜2×10-3°，姿态角速度控制精度为：。相应的控制力矩变化曲线如图3 所示。图中可见，在整个仿真过程中控制力矩没有超过航天器控制输出上限，表明了本文所提控制方法具有一定的工程应用价值。

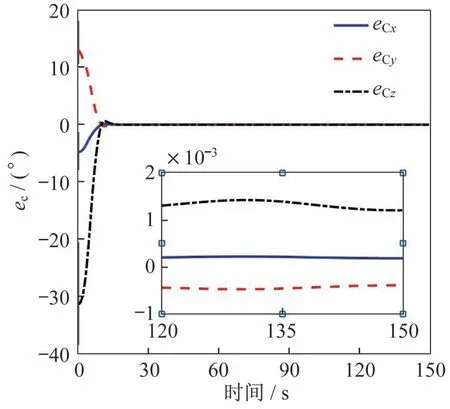
图1 姿态跟踪误差（情况1）Fig.1 Attitude tracking errors（Case 1）

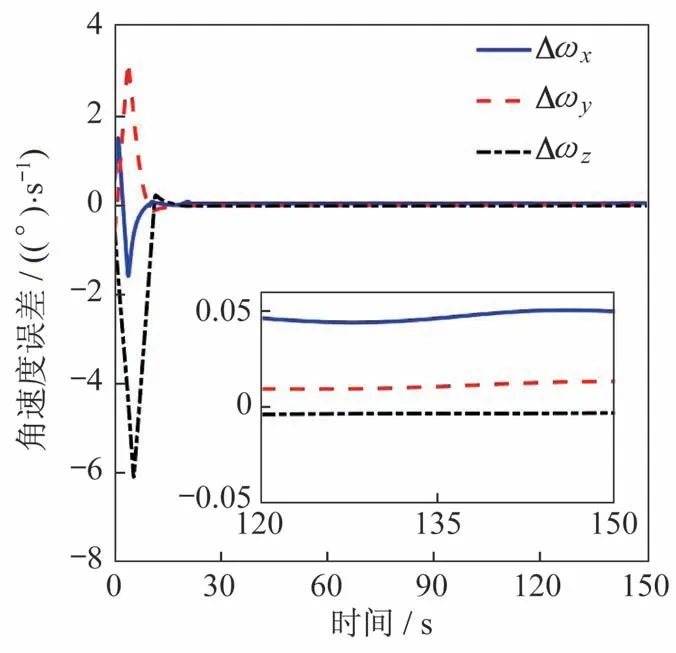
图2 角速度跟踪误差（情况1）Fig.2 Angular velocity tracking errors（Case 1）

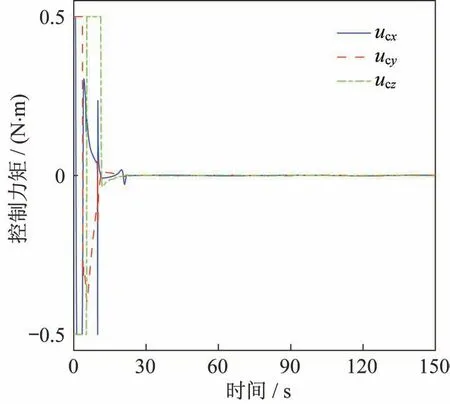
图3 控制力矩（情况1）Fig.3 Control torques（Case 1）

情况2 仿真结果如图4～图6 所示，仿真时间设置为300 s。图4为航天器姿态跟踪误差，图5为角速度跟踪误差。图中可见，航天器姿态运动误差在150 s 左右收敛到稳态，通过系统状态在120 s 到150 s，以及收敛后的曲线放大图可以看出，与本文设计的控制器式（22）的仿真结果相比，无论是误差收敛时间还是最后的稳态控制精度，本文所设计的控制器均优于文献［12］。

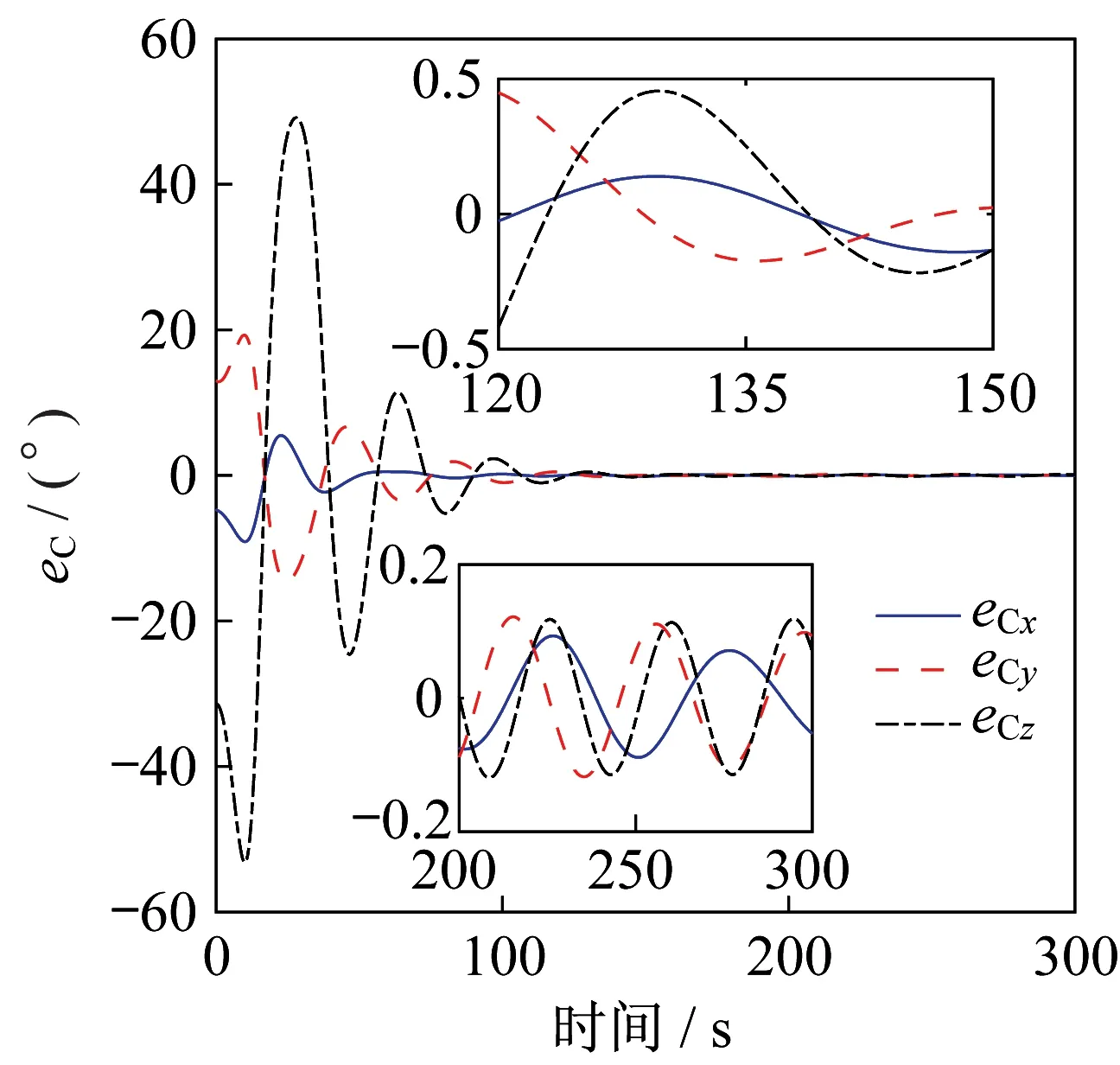
图4 姿态跟踪误差（情况2）Fig.4 Attitude tracking errors（Case 2）

图5 角速度跟踪误差（情况2）Fig.5 Angular velocity tracking errors（Case 2）

图6 控制力矩（情况2）Fig.6 Control torques（Case 2）

此外，对于在轨运行航天器来说，能量消耗是决定其在轨运行寿命的一个关键因素。为了进一步比较两种情况的仿真结果，定义能量消耗函数为

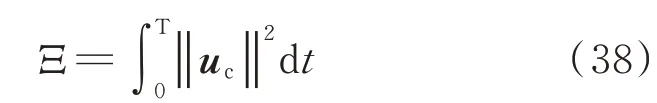
式中：T=150 s。

两种情况的能量消耗曲线如图7 所示。图中可见，与文献［12］控制器相比，本文所设计的控制方法可以在保证较高的控制性能的同时，将能量消耗降低72%左右。通过上述两种情况的仿真结果及对比分析可以发现，在系统存在外部干扰和模型不确定性情况下，本文所提出的控制方法可以有效地解决航天器姿态跟踪控制问题，且与传统的PD 控制器相比，可以实现更好的控制效果。

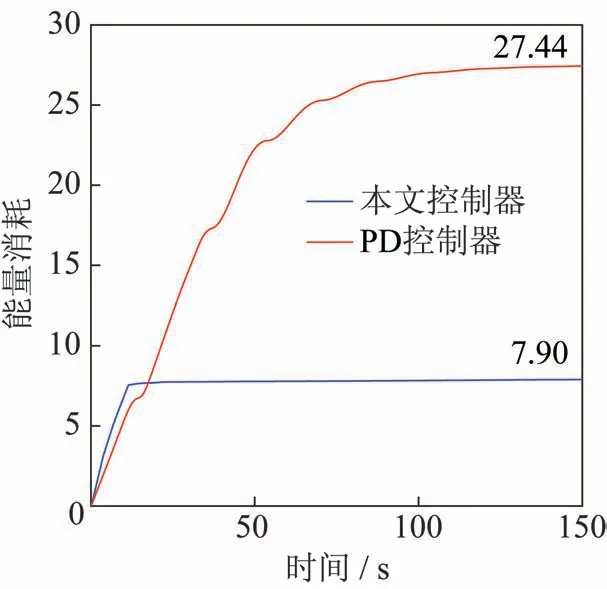
图7 能量消耗Fig.7 Energy consumption

5 结束语

本文研究了刚体航天器姿态跟踪控制问题，在姿态跟踪系统存在模型不确定性和外部干扰情况下，推导了SO（3）上航天器相对姿态动力学模型。在模型中，采用方向余弦矩阵描述航天器姿态运动，且通过引入非负定的势函数描述姿态跟踪误差，将动力学模型转换成了易于控制器设计的形式，并有效避免了用其他姿态描述方式表示姿态时，引起的奇异或退绕问题。基于此模型，设计了自适应反步姿态控制器，保证了闭环控制系统的最终一致有界收敛，并通过Lyapunov 稳定性分析方法，证明了控制系统的收敛特性。最后，对所设计的控制算法进行了仿真校验，且与文献［12］中的PD 控制器进行了对比分析。结果表明，本文提出的控制方法收敛速度快、控制精度高、能量消耗低，具有一定的工程应用价值。此外，本文的研究对象为刚体航天器，而为了增加航天器的在轨功能，一般都配备有太阳电池阵、天线等柔性附件。柔性附件在轨会发生振动，且振动信息一般无法测量。因此，未来的一个研究方向是如何将本文设计的控制算法用于解决柔性航天器姿态控制问题。