空间站柔性太阳电池翼对日跟踪控制

赵 真，王 碧，钱志源，陈国平

（1.南京航空航天大学机械结构力学及控制国家重点实验室，江苏南京 210016；2.上海宇航系统工程研究所，上海 201109）

0 引言

我国载人航天工程已进入空间站研制阶段，计划在2022 年前后全面建成。空间站采用三舱“T 型”布局，分别为核心舱、实验舱Ⅰ和实验舱Ⅱ。在核心舱两端分别留有载人飞船和货运飞船对接口，如图1所示［1］。

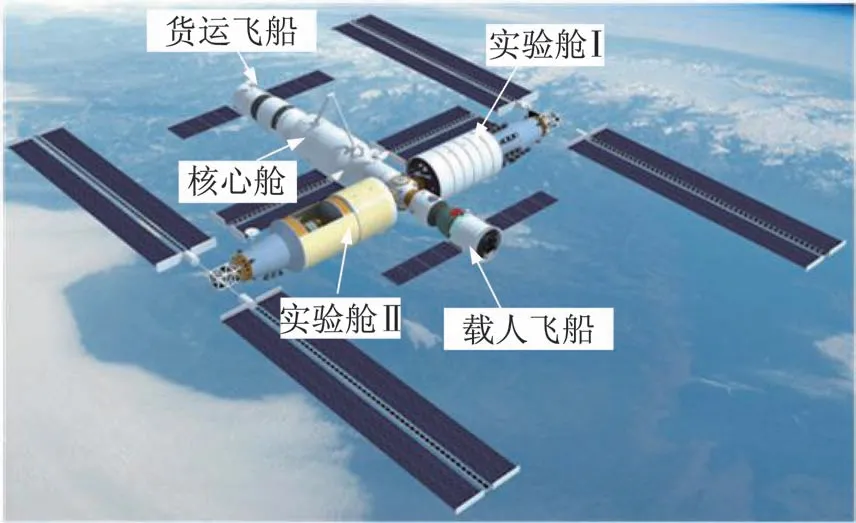
图1 中国空间站构型Fig.1 Schematic diagram of Chinese Space Station（CSS）

为保证我国空间站15 a 在轨运行期间能源平衡，在实验舱Ⅰ、Ⅱ末端各配置1 套Alpha 对日定向装置和2 套太阳电池翼，如图2 所示。为适应空间站90 min 每圈的轨道周期，Alpha 对日定向装置持续驱动太阳电池翼和末端桁架组成的柔性负载以0.065（°）/s 的角速度对日跟踪，将太阳能转化为电能。

图2 空间站太阳电池翼驱动控制系统Fig.2 Schematic diagram of the solar cell wing drive control system of CSS

由于柔性负载的大尺寸（翼展大于55 m，面积约270 m2）、大惯量（3.4×105kg·m2）、超低频（基频小于0.07 Hz）、模态密集（2 Hz 以内频率超过600 阶）等特点，为柔性负载地面模态试验、数学建模、模型正确性估计等带来难度。Alpha 对日定向装置长期在轨工作过程中的性能退化对长期保持低速稳定驱动控制带来挑战。因此，突破空间站大柔性太阳电池翼高稳定驱动控制技术，对于保障空间站能源安全和平稳运行至关重要。

以国际空间站（International Space Station，ISS）为例，与Alpha 对日定向装置输出端连接的末端桁架上配置4 个太阳 电池翼，如图3 所示［2］，翼展超过70 m，面积552 m2，1 阶频率0.06 Hz，转动惯量5.4×105kg·m2。为实现柔性负载稳定驱动，采用带4 阶Butterworth 低通滤波器的速度、位置双环系统，控制参数的确定通过构造与两环控制带宽相关的受限优化函数（Constrained Optimization Scheme）进 行综合［3-4］。

图3 国际空间站Alpha 对日定向装置与太阳电池翼Fig.3 Solar Alpha rotary joint（SARJ）and solar cell wings of ISS

随着现代航天器柔性附件（太阳翼、天线、桁架等）尺寸越来越大，对于大柔性附件高稳定驱动控制系统的研究，得到了学者们重视［5］。除国际空间站上的应用外，BONG 等［6］在带有大柔性太阳翼的哈勃望远镜（Hubble Space Telescope，HST）指向控制中，提出采用带陷阱滤波的鲁棒控制方案，并与经典PID控制进行对比，认为该方法在确保平台速度稳定度和挠性振动抑制上有较好的效果。YOSHIRO 等［7］在日本工程试验卫星八号（Japan Engineering Test Satellite Ⅷ，ETS-Ⅷ）上，为解决柔性天线大角度跟踪指向控制，采用线性插值规划控制（Linearly Interpolated Gain Scheduling Controller）进行运动拟合，也得到了较好的速度稳定度效果。针对线性控制器对大柔性体非线性系统调节能力不足的问题，学者们考虑将输入成型控制、鲁棒控制［8］、变结构控制、自适应控制等应用于大柔性体伺服控制，以满足系统动、静态性能指标［9］。

本文以空间站大柔性太阳电池翼高稳定对日跟踪控制为研究对象，推导柔性太阳电池翼动力学模型和开展有限元分析，建立Alpha 对日定向装置机电系统模型和非线性传动系统模型；针对柔性负载低频和传动系统非线性对控制性能的影响，设计带变速规划和柔性振动抑制的速度、位置双环控制系统；并通过仿真校验，证明控制方案的有效性。

1 控制系统建模

1.1 柔性太阳电池翼动力学建模

参考我国空间站Alpha 对日定向装置和太阳电池翼的相对布局关系，采用混合坐标法和有限元法对柔性负载（末端桁架和两侧太阳电池翼的组合体）进行离散化，并用Lagrange 方程建立柔性动力学模型，得到太阳电池翼驱动力矩与转速的状态方程［10］。

建模中引入空间站本体坐标系{b}，末端桁架固连随动坐标系{α}。{α}原点Oα在Alpha 对日定向装置与末端桁架连接法兰面几何中心，rb为空间站本体坐标系{b}原点Ob到末端桁架坐标系{α}原点Oα的矢径，rα，j为桁架和太阳电池翼组成的柔性体上任意点j相对于坐标系{α}的矢径，δα，j为j点的变形位移，Rb，j为j点相对于坐标系{b}的位移矢量，具体描述如图4 所示。

图4 单自由度转动柔性负载坐标系定义Fig.4 Definition of the coordinate system of single-degree-of-freedom rotating flexible body

矢径Rb，j及其导数的表达式为

式中：ωα=(ωα，x，ωα，y，ωα，z)为{α}系相对于{b}系的角速度矢量在{b}系中的描述，其中，ωα，y为Alpha对日定向装置转动角速度。

假设Cb2α为由{b}系到{α}系的变换矩阵：

式中：θα为Alpha 对日定向装置转过的角位移（yα轴方向）。

柔性负载上任意点j的速度公式（2），转换到随动系{α}系下描述如下：

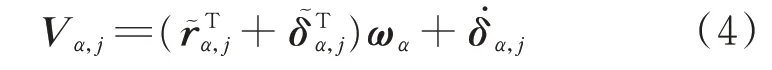
假设向量δα表示柔性负载上所有节点的线弹性变形，可用柔性负载模态分析得到的基向量的线性组合表示：

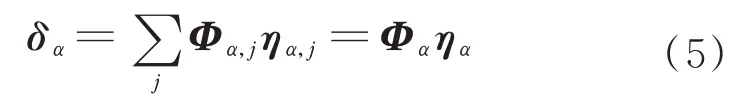
式中：Φα=(Φα，1，Φα，2，…，Φα，j，…，Φα，q)表示柔性负载的振型基?向量阵；ηα=(ηα，1，ηα，2，…，ηα，j，…，ηα，q)T表示?柔性负载的模态坐标，其中，q为柔性负载的总节点数。

经运动学描述，可得系统动能T和势能V表达式为式中：mα，j为柔性负载上的j点集中质量；Κα为刚度矩阵为柔性负载的固有频率矩阵（n×n阶）。

Jα为柔性负载相对坐标系{α}原点Oα的转动惯量矩阵：

Fα为柔性负载振动对其转动的耦合系数矩阵：

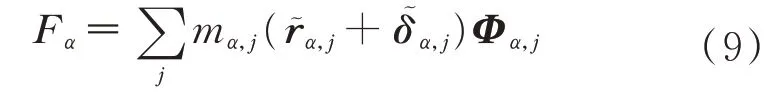
系统Lagrange 函数为

将式（6）、式（7）代入式（10），建立第2 类Lagrange 方程如下：

描述系统绕Alpha 对日定向装置转动和弹性振动的系统动力学方程为

式中：Tα为Alpha 对日定向装置驱动力矩；ζα=diag(ζα，1，ζα，2，…，ζα，n)为柔性负载各阶模态的阻尼比对角阵；Ωα为柔性负载圆频率对角阵Ωα=diag(ωα，1，ωα，2，ωα，3，…，ωα，n)，n为模态阶数，有

将式（12）、式（13）用状态方程描述，输入为Alpha 对日定向装置驱动力矩Tα，y，输出为柔性负载转动角加速度αα，（y可由αα，y积分得到角速度ωα，y）。状态方程的状态量为柔性负载的模态坐标及其变化率，可通过对模态坐标动态变化评估各阶频率在振动响应中所占权重和演化规律，并结合模态基向量得到每1 个离散点的位移量。

状态方程形式如下：

式中：A、B、C分别为2n×2n、2n×1、1×2n的系数矩阵；D为实数系数；n为柔性负载模态分析频率截断后的保留阶数。则有

由式（15）的第1 式调整后为

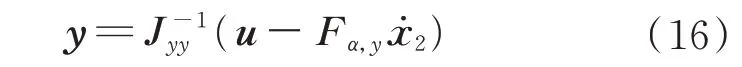
将式（16）代入式（15）第2 式，可得状态方程（14）的第1 式。推导过程如下：

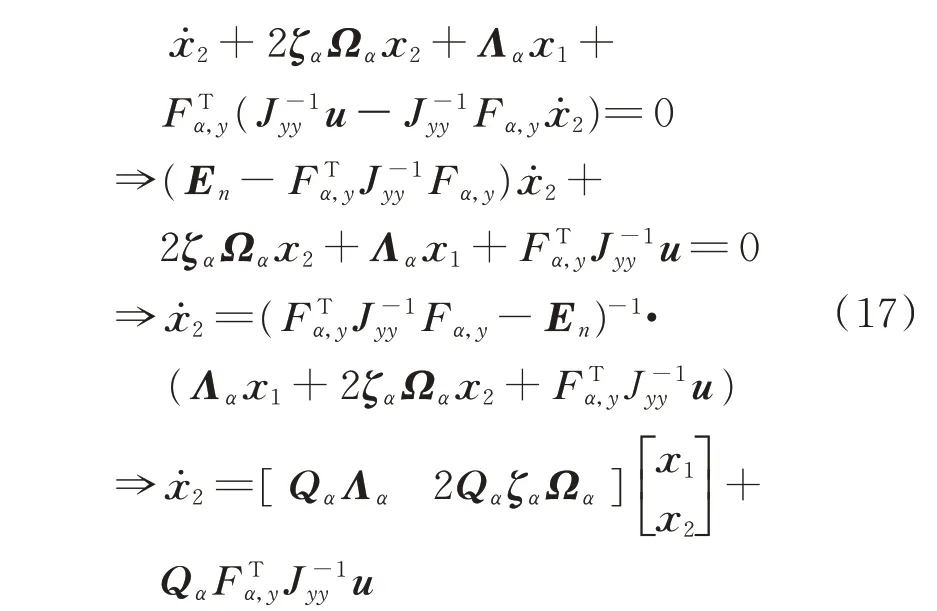
又式（15）的第2 式代入第1 式，调整后可得状态方程（14）的第2 式如下：

得Alpha 对日定向装置驱动力矩与柔性负载转动角加速度（输出量积分得到角速度）的状态方程为

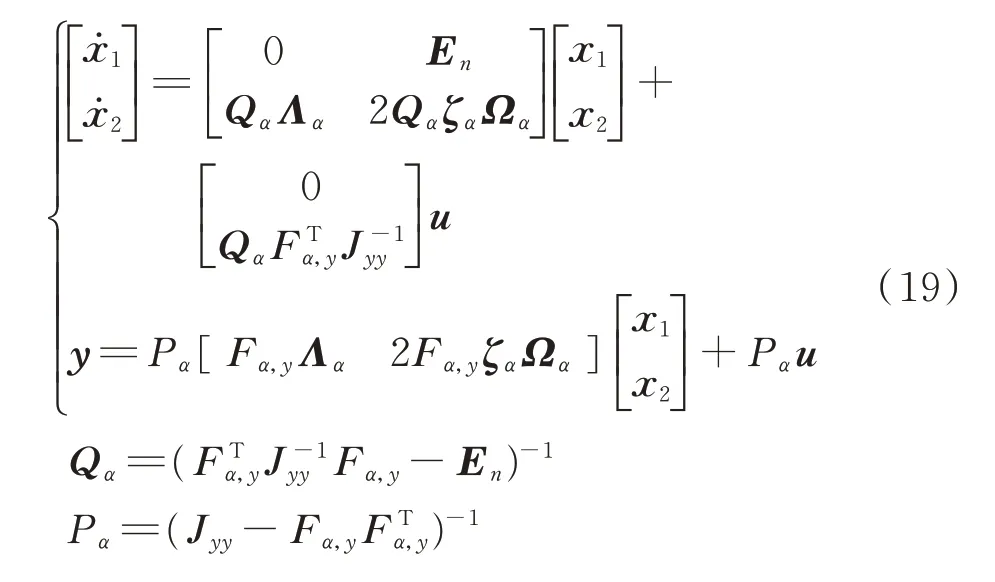
1.2 太阳电池翼模态分析与截断

柔性体状态方程如式（19）所示，为得到方程系数，需要对太阳电池翼进行模态分析，获取其各阶频率和振型。如空间站太阳电池翼这样尺寸大、基频低、模态密集的结构，直接采用模态截断仍然将导致模型阶数较高。先根据伺服控制带宽进行初次截断，再依据惯性完备性准则和模态有效质量进行模态筛选［11］。

根据末端桁架和太阳电池翼的设计方案，用MSC.Nastran 建立非线性有限元模型，如图5 所示。设转轴正方向为yα、原点为Alpha，对日定向装置与末端桁架连接法兰的几何中心。有限元模型节点41 976个，各类单元41 465个，各类多点约束连接237个。采用非线性动力学求解器SOL 106对柔性负载进行模态分析，其中前3阶主模态如图6～图8所示。

图5 太阳电池翼有限元模型Fig.5 Finite element model of solar cell wings

图6 太阳电池翼第1 阶主模态两对称振型（0.066 9 Hz）Fig.6 The first main mode of solar cell wings（0.066 9 Hz）

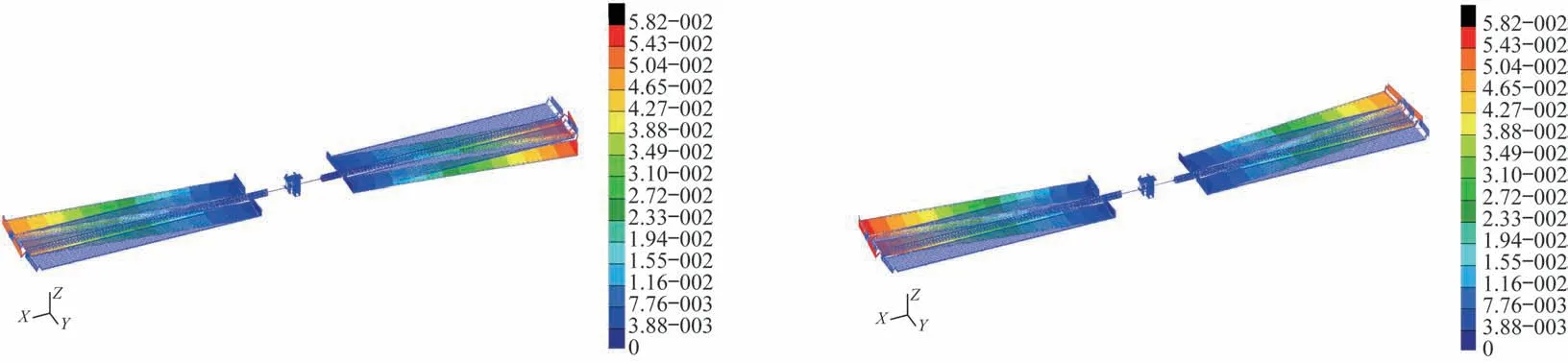
图7 太阳电池翼第2 阶主模态两对称振型（0.067 2 Hz）Fig.7 The second main mode of solar cell wings（0.067 2 Hz）

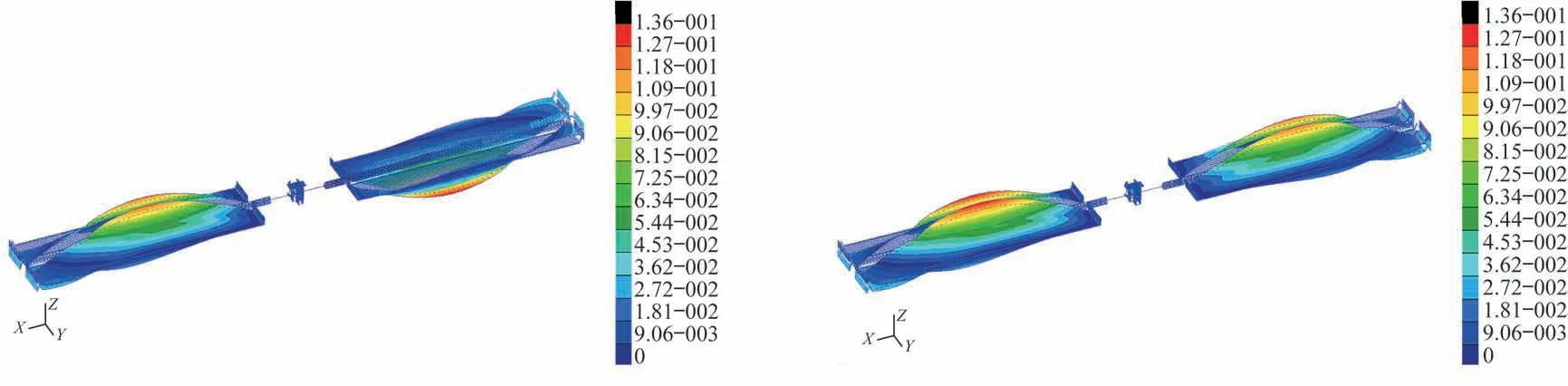
图8 太阳电池翼第3 阶主模态两对称振型（0.123 0 Hz）Fig.8 The third main mode of solar cell wings（0.123 0 Hz）

对1.0 Hz和2.0 Hz截止频率下的模态阶数和模态有效质量进行汇总，见表1。

表1 不同截止频率下的模态阶数和模态有效质量Tab.1 Modal orders and effective mass at different cutoff frequencies

由于柔性负载在Alpha对日定向装置驱动下实现绕坐标系{α}的yα轴转动，在驱动力矩Tα，y作用下，柔性负载弹性变形主要体现在zα轴方向的平动和绕yα轴的转动。而模态截断至2.0 Hz或1.0 Hz，其RY向模态有效质量已经大于98%，保留的动力学特性可为工程接受。频率2.0 Hz内的模态有638阶，需要根据模态有效质量进一步完备性筛选，减少系统阶数。

1.3 Alpha 对日定向装置机电系统建模

Alpha 对日定向装置采用永磁同步电机配合高精度角度传感器，实现宽调速范围的多级闭环驱动控制。取永磁体基波磁场轴线（转子N极）为d轴，q轴顺着旋转方向超前d轴90°电角度。电机模型遵循如下假设：1）忽略磁路饱和、磁滞和涡流影响，磁路线性，无阻尼；2）定子绕组三相对称，各绕组轴线在空间上互差120°；3）电机电势正弦，定子电流在气隙中只产生正弦分布磁势，忽略磁场高次谐波［12］。

永磁同步电机动力学模型为

式中：uq、ud为交轴、直轴电压；iq、id为交轴、直轴电流；Lq、Ld为电机直轴、交轴同步电感，Lq=Ld；ψf为转子永磁体的励磁磁链；ωi为转子电角速度（转子机械角速度ωm=ωi/Pn）；Rs为定子电阻；Pn为定子绕组极对数；Jm为电机机械转动惯量；Te为电磁转矩；Bm为黏性摩擦系数；Tm为Alpha 对日定向装置电机端输出力矩，通过传动系统放大，并克服传动摩擦力矩TD后，为Alpha对日定向装置驱动力矩Tα，对应式（19）中的u。

1.4 传动系统建模

1.4.1 间隙模型

Alpha 对日定向装置的多级减速器会带来设计中不可忽略的传动间隙，在控制系统设计中需克服间隙引起“死区”非线性。Alpha 对日定向装置减速器装配间隙等效模型如图9 所示。

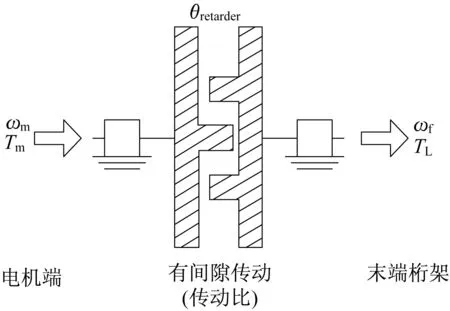
图9 传动间隙等效模型Fig.9 Equivalent model of transmission gap

图中：θretarder为减速器折算到柔性负载端的间隙；Tm、ωm为Alpha 对日定向装置电机端力矩和转动角速度；TL、ωf为Alpha 对日定向装置输出端驱动力矩和转动角速度。

当传动轴弹性形变角度θmf满足切换条件|θmf| ≤θretarder/2 时，Alpha 对日定向装置输出端悬空：

式中：输出驱动力矩TL为零；电机端负载力矩Tm为传动系统摩擦力矩TD，反映传动摩擦特性；i为减速比。

当间隙消除，即|θmf|＞θretarder/2 时，

式中：Alpha 对日定向装置驱动力矩TL为净扭转形变力矩。

1.4.2 摩擦模型

传动系统中的摩擦力矩会降低传动效率，并且在低速转动时由于动、静摩擦力矩的切换导致“爬行现象”。但摩擦力矩的存在也可以有效减缓柔性负载振动对Alpha 对日定向装置电机的反作用力矩，实现振动隔离，保护驱动电机。

结合试验数据，可拟合出Alpha 对日定向装置的传动摩擦特性。采用动态LuGre 模型拟合，模拟静、动摩擦间的切换。摩擦力矩TD数学表达式如下：

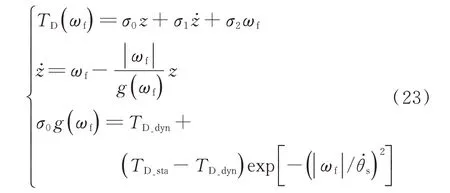
式中：ωf=ωα，y为Alpha 对日定向装置转动角速度；z为平均变形量；σ0为刚性系数；σ1为滑动阻尼系数；σ2为黏性摩擦系数；TD_dyn为库伦摩擦力矩；TD_sta为最大静摩擦力矩；θ˙s为Stribeck 特征速度［13］。

假设传动系统静摩擦力矩为80 N·m，动摩擦力矩为60 N·m，构造摩擦力矩TD是转动角速度ωf的函数，LuGre 摩擦曲线如图10 所示。

图10 LuGre 摩擦模型曲线Fig.10 LuGre friction model curve

2 稳定跟踪控制方案设计

为提高驱动稳定性，采用带运动规划和振动抑制的速度、位置双闭环伺服方案。控制系统框图如图11 所示。

图11 对日定向装置驱动控制框图Fig.11 Drive control block diagram of the SARJ

2.1 变速规划方案

提高启动和制动等变速过程的平稳性，降低柔性体低频扰动载荷，采用Heaviside 五次样条变速规划策略，实现1、2 阶导数连续，且角度和角速度规划匹配。在调速过程中，通过Heaviside 变速规划，也可克服传动间隙影响，表达式如下：

2.2 位置环和速度环方案

位置环、速度环调节器为消除静差，提高跟踪精度，引入积分环节。但传动间隙θretarder会导致末端反馈测量偏差较大，造成速度环调节器积分累积超过限幅阈值，引发系统振荡。因此，在位置环和速度环都引入积分分离控制器。

当被控量与规划值偏差较大时，取消积分作用，以免积分导致系统稳定性降低；当被控量接近规划值时，引入积分控制，消除静差，提高跟踪精度［14］。

积分分离控制算法表示为

式中：Δt为采样时间；β为积分项的开关系数，

2.3 振动抑制方案

太阳电池翼受到外界扰动时，会激发其弹性低频振动，且持续时间较长。为快速抑制柔性太阳电池翼受外界扰动载荷引起的振动，在速度调节器前，设计特定频率的陷阱滤波器（Notch Filter）：

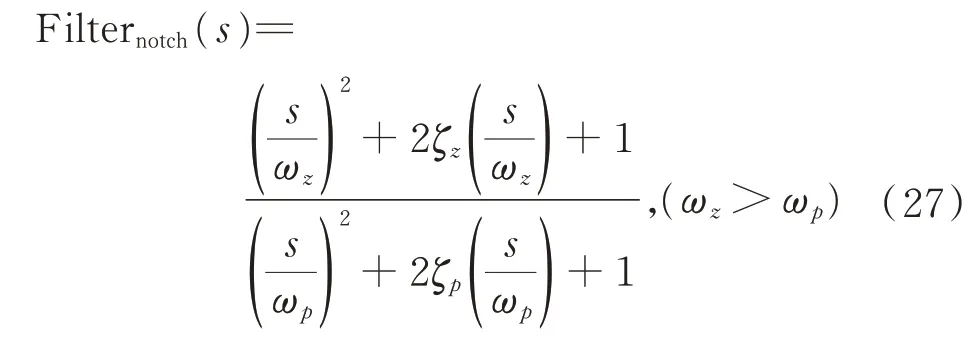
通过设置陷阱滤波器参数ωz、ωp、ζp、ζz，使滤波器作用区域限制在太阳电池翼基频附近。参考模态分析结果，柔性负载弹性主要体现在1 阶模态上（0.066 9 Hz），取ωz=0.42，ωp=0.377，ζp=0.70，ζz=0.02。陷阱滤波器传递函数Bode 图如图12所示。

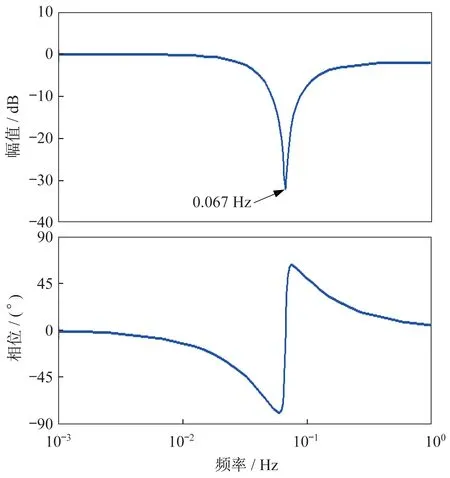
图12 陷阱滤波器幅频、相频曲线Fig.12 Phase frequency and amplitude frequency curves of the notch filter

3 仿真校验

空间站运行在380～410 km 之间的轨道高度，为确保柔性太阳翼阵面与太阳光入射方向垂直，常见工况为：Alpha 对日定向装置加电启动，从停转状态加速到0.300（°）/s，开始对太阳进行搜索捕获，捕获太阳后Alpha 对日定向装置转入空间站轨道角速度0.065（°）/s 持续对日跟踪模式。

假设，柔性负载转动惯量为

主模态频率fa=（0.066 9，0.067 2，0.123 0，0.180 0，0.181 7，…）Hz。

柔性负载振动对其转动的耦合系数矩阵为

得到反映柔性负载传递函数Bode 图（输入驱动、输出角速度）如图13 所示。图中，蓝色实线为其幅频特性、相频特性曲线，红色虚线为简化负载为刚体时的动态特性，两者差异明显。由于给出的是Alpha 对日定向装置转动方向的特性，由Bode 图可知0.067、0.123、0.180、0.882、0.956 Hz 等频率对其动力学振动特性起主导作用。

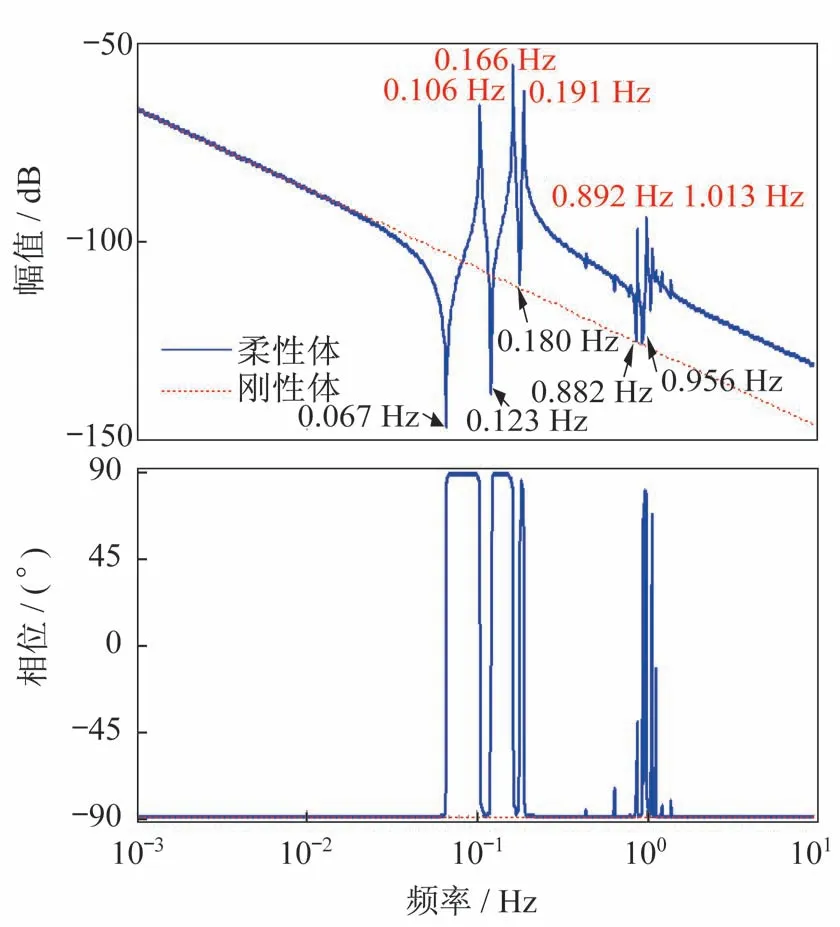
图13 柔性负载动力学特性Bode 图Fig.13 Bode diagram of flexible body transfer function

设Alpha 对日定向装置永磁同步电机、传动系统的参数见表2［15］。

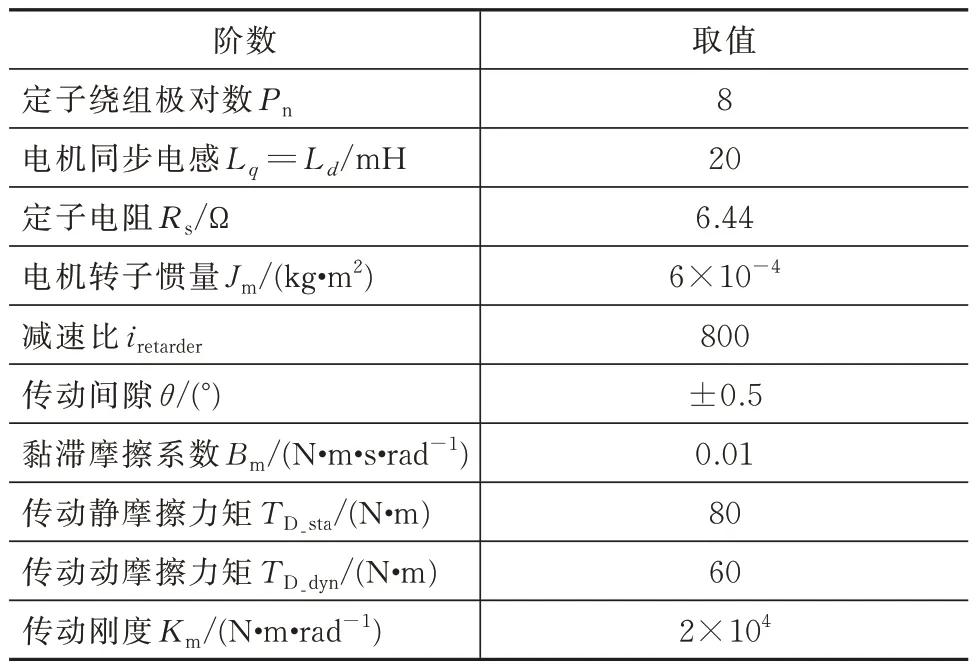
表2 Alpha 对日定向装置参数Tab.2 Input parameters of the SARJ

设计控制参数，位置环控制带宽0.027 8 Hz；速度环控制带宽0.039 5 Hz。仿真中柔性负载的启动规划时间180 s，分析结果如图14～图19所示。

图14 伺服角速度与规划指令角速度Fig.14 Servo angular velocity and planning angular velocity

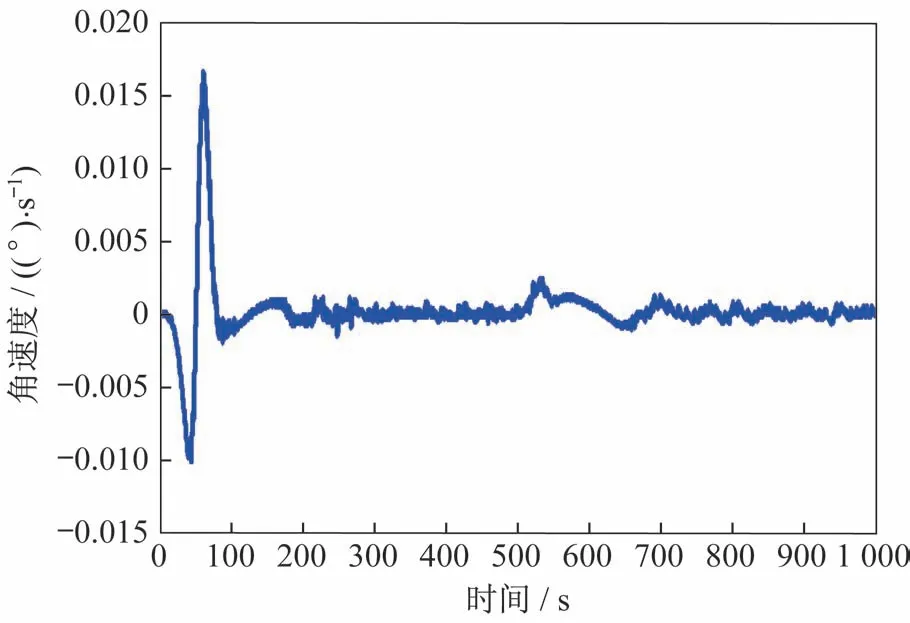
图15 伺服角速度与规划指令角速度偏差Fig.15 Deviation between the servo angular velocity and the planning angular velocity

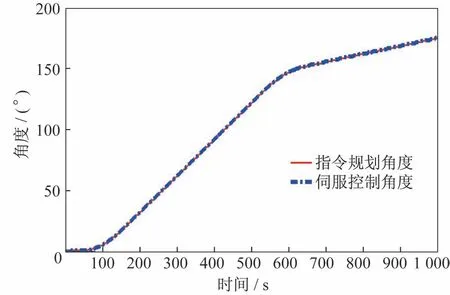
图16 伺服角度与规划指令角度Fig.16 Servo angle and planning angle of the SARJ

图17 伺服角度与规划指令角度偏差Fig.17 Deviation between the servo angle and the planning angle

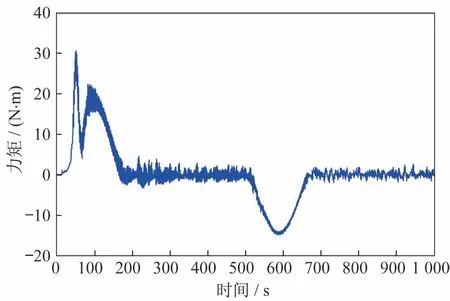
图18 Alpha 对日定向装置输出力矩Fig.18 Output torque of the SARJ

图19 前3 阶主频率模态坐标Fig.19 Modal coordinates of the first third order frequencies

从图14～图17 可知，在启动规划过程中受传动间隙和传动摩擦影响，存在速度跟踪偏差，180 s 规划完成时已经实现稳定跟踪。跟踪精度优于0.3°，速度偏 差±0.005（° ）/s，稳定度优于 7%＠0.065（°）/s。

从图18 和图19 可知，Alpha 对日定向装置的启动和变速过程中驱动力矩不大于30 N·m。稳速运行期间，驱动力矩不大于5 N·m。驱动过程中激发柔性负载第1、3 阶模态，当驱动处于稳速转动后，低阶柔性振动也得到抑制。

4 结束语

本文研究空间站柔性太阳电池翼高稳定对日跟踪控制问题，推导了柔性太阳电池翼驱动力矩与转速状态方程，建立考虑传动间隙和传动摩擦的Alpha 对日定向装置模型，提出一种带运动规划和振动抑制的速度、位置双闭环伺服控制方法。文中给出的仿真算例说明了该方法在实现柔性负载稳定驱动的有效性。文中所述方案控制性能好于国际空间站Alpha 对日跟踪控制设计指标：稳态跟踪偏差不大于 2°，速度稳 定度优于10%＠0.065（°）/s［3-4］。