敏捷SAR 卫星平台载荷一体化控制方法研究

张永强，王 赟，刘德庆，陈筠力，于迎军，吴敬玉

（1.北京跟踪与通信技术研究所，北京 100094；2.上海卫星工程研究所，上海 201109；3.上海航天控制技术研究所，上海 201109；4.上海航天技术研究院，上海 201109）

0 引言

近年来，随着星载合成孔径雷达（Synthetic Aperture Radar，SAR）系统技术的发展，特别是轻型天线等技术的应用，使得性能高、质量小、反应快、成本低的轻量化SAR 卫星的研制成为可能。轻量化SAR 卫星通过协同工作的方式，在特定目标的搜索发现、识别确认、跟踪监视、目标指示、长时间连续覆盖、高频多重覆盖等方面越来越显示出其特有的优势，成为国内外航天领域研究的热点之一［1］。

采用相控阵体制的SAR 天线具备模块化、波束赋形功能强大等优点，易实现与卫星平台一体化设计，在轻量化设计方面具有明显优势［2］。而由于具备二维载荷波束电扫描能力的传统大型相控阵天线结构复杂，造价高昂，质量较大，难以适用于小卫星。故需要以载荷有限波束扫描能力与平台的机动能力配合工作来实现传统大型卫星的成像效果。此外，可以通过卫星的高精度敏捷姿态机动能力增加卫星的工作模式，使得卫星工作模式灵活机动，增强卫星获取信息的能力。如：通过卫星的姿态机动或波束扫描，以不同的视角观测，可以获取被观测区域的更多维信息量，增强目标识别能力；通过二维姿态导引，可以提高SAR 的图像质量［3］；通过机动和波束扫描结合，还可以更好地进行多目标获取，提高多目标获取能力［4］。文献［5］提出可通过敏捷卫星的姿态机动实现SAR 滑动聚束成像。文献［6-10］研究了敏捷卫星通过姿态机动的方式，实现聚束成像、视频成像等成像模式，并给出了相应的姿态机动策略。但是，这些研究均是从敏捷平台配合固定有效载荷的方式出发，通过姿态机动完成成像过程所需载荷波束扫描。在此基础上，使用敏捷平台配合具备一维波束扫描能力的SAR 载荷，将具备更高的灵活性和成像能力。

同时，为提高图像信息获取能力，轻量化SAR卫星也往往采用大尺寸、大质量的天线，并且对卫星姿态敏捷机动能力提出更高的要求［11］。使用传统飞轮作为主执行机构，只能实现0.1～1.0（°）/s 的最大机动角速度，难以满足高时间分辨率要求［11］。使用单框架控制力矩陀螺（Single Gimbal Control Moment Gyroscopes，SGCMG）作为小卫星的姿态机动控制执行机构，可有效提高敏捷平台姿态机动能力，更好地配合载荷完成成像任务。文献［12-13］论述姿态机动路径快速规划和跟踪控制结合的姿态闭环控制策略，提出了避免SGCMG 奇异的方法。

本文系统性地分析了具备一维波束扫描能力的小型SAR 卫星通过平台机动与载荷波束扫描配合成像时对姿态的需求。针对成像姿态需求对平台快速机动的要求，提出了采用小型化SGCMG 作为执行机构的方案，通过改进型递阶饱和控制方法，实现卫星高指向精度高稳定度控制与敏捷机动。

1 采用SGCMG 的动力学模型

系统本体系相对于参考系的姿态用四元数Q=q0+q1i+q2j+q3k表示，对于本体系相对于参考系的角速度在本体系分量ω=[ωx ωy ωz]T，姿态变化的角速率可描述为［14］

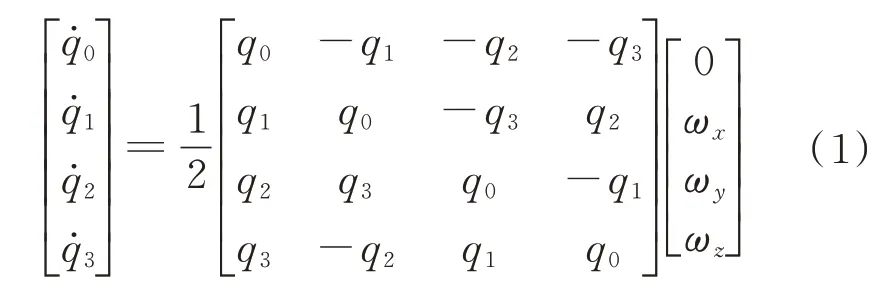
对于采用SGCMG为执行机构的系统，卫星动力学在卫星本体坐标系的表示为［15-16］

式中：I为系统惯量矩阵；T为作用于系统的外力矩；ω×为ω的叉乘或反对称斜方阵；为SGCMG 系统的 框架角速度矢量；H为SGCMG 系统合成角动量在本体坐标系下的表示；C为SGCMG 系统输出的力矩矩阵。

2 成像基准姿态确定

2.1 条带成像

条带模式成像要求控制天线波束指向在方位向和距离向固定不变，以进行连续高分辨率的成像。敏捷SAR 卫星通过控制平台侧摆飞行的方式，保持SAR 天线波束实际指向与飞行方向之间的固定夹角，实现条带模式成像。同时，利用俯仰方向姿态偏置实现大角度斜视保证高分侦察的时效性，SAR 天线距离向波束扫描实现目标快速切换，提高区域观测响应能力，条带成像示意图如图1所示。图中：θL为成像距离向下视角（简称“下视角”）；θ为成像方位向斜视角（简称“斜视角”）；φcs为卫星左右侧视基准角度（简称“侧视角”）。

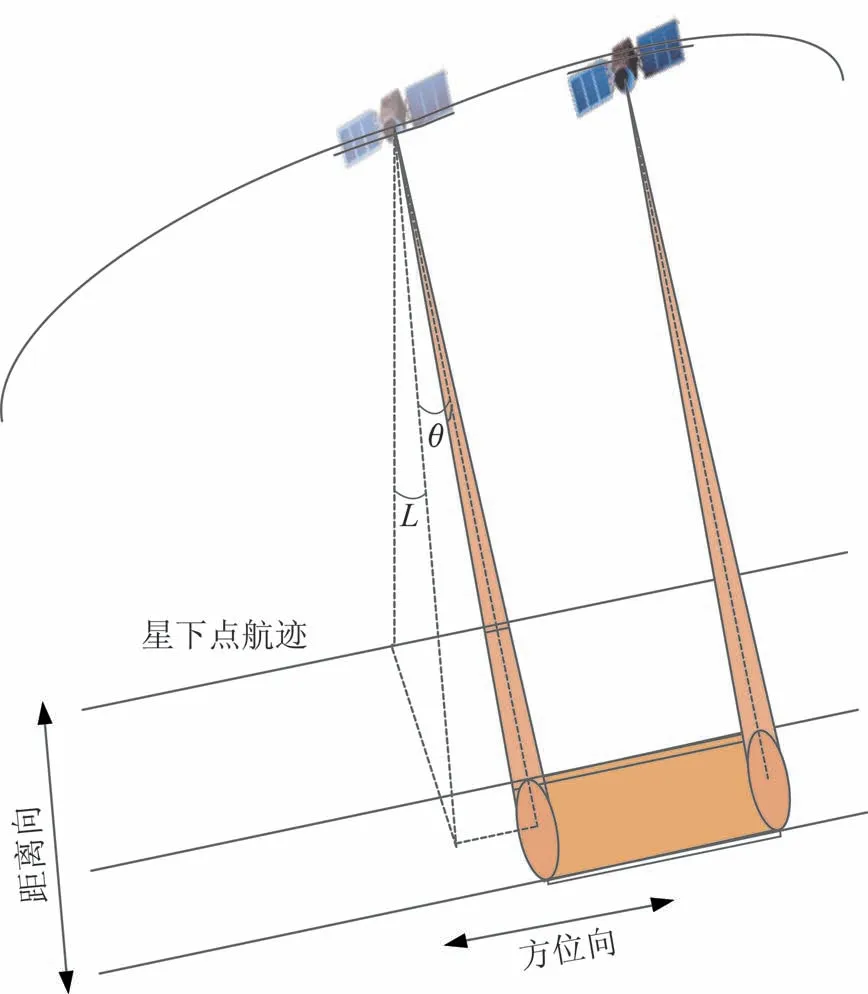
图1 条带成像示意图Fig.1 Schematic diagram of strip imaging

为提高敏捷性，平台通过绕惯量主轴机动的方式配合载荷成像。采用本体坐标系相对轨道坐标系 123 转序或 312 转序计算基准姿态角和雷达波束扫描角λ，卫星本体相对轨道坐标系姿态通过绕本体Xb轴和Yb轴旋转后不需要再绕Z轴旋转，故ψm=0，第一次绕Xb轴旋转实现左右侧视，故φm=φcs。

绕Yb旋转角度θm和雷达波束扫描角λ计算方法如下：

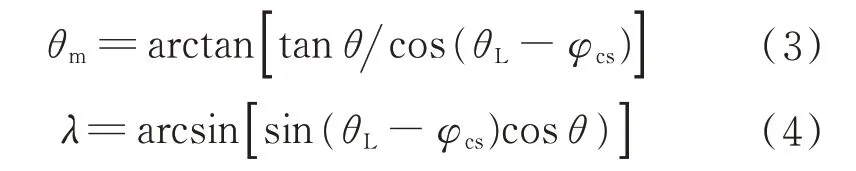
将基准姿态角（123 转序或312 转序）转换为基准姿态四元数qm，基准姿态角速度为ωm=[ 0 0 0]T。

2.2 多条带拼接成像

卫星通过绕Yb轴姿态机动实现从前斜视到正侧视再到后斜视的不同角度下观测，配合载荷距离向波束扫描，通过扫描条带拼接，可实现大幅宽成像。

多条带拼接成像的基准姿态建立过程与条带成像相同（如图2 所示），但是对姿态机动速度要求高，前一次成像结束到下一次成像开始之间的姿态机动必须在指定的时间内完成，否则影响后一次成像性能，甚至导致多条带拼接成像任务失败。

图2 多条带拼接成像示意图Fig.2 Schematic diagram of multi-strip splicing imaging

2.3 滑动聚束成像

滑动聚束模式通过控制天线波束在方位向的旋转速度，从而控制天线辐照区在地面的移动速度，实现高分辨率大面积滑动聚束成像，如图3 所示。传统大型相控阵天线通过波束捷变切换方式实现旋转速度控制，受角度量化误差影响，无法实现连续变化。对于敏捷SAR 卫星，通过控制平台连续转动实现波束控制，可以更精确地实现滑动聚束模式，提高SAR 方位向分辨率。

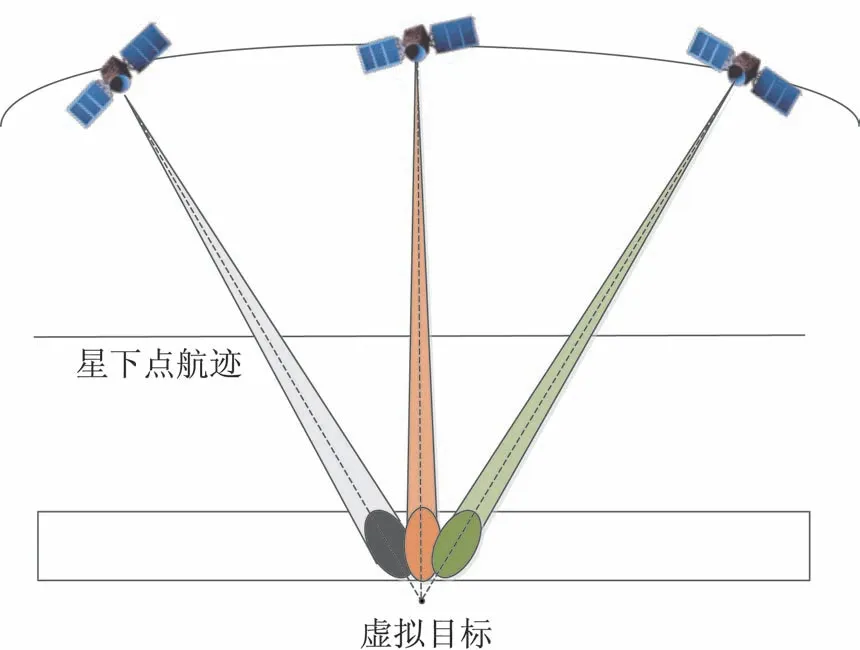
图3 滑动聚束成像示意图Fig.3 Schematic diagram of sliding bunching imaging

给定转动中心虚拟目标，可建立卫星指向目标的参考姿态基准。地心至目标的矢量ret在轨道坐标系的表示为

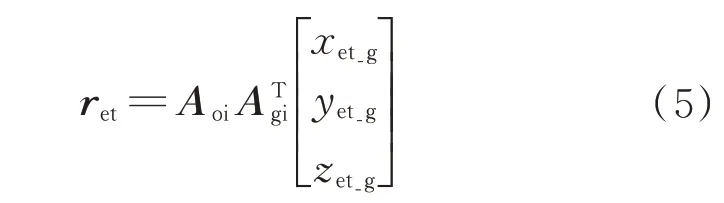
式中：[xet_gyet_gzet_g]T为在WGS84 地球固联坐标系下的目标点坐标；ATgi为J2000 惯性坐标系到WGS84 地球固联坐标系的旋转矩阵；Aoi为J2000 惯性坐标系到轨道坐标系的旋转矩阵。

卫星至地心的矢量在轨道坐标系表示为rse=[0 0r]T，则卫星到目标的矢量为

卫星指向虚拟目标示意图如图4 所示。为了确定相对轨道坐标系的基准姿态，将指向表示在轨道坐标系下，如图5 所示。r1为卫星无姿态偏置时电扫方向，为了实现电扫指向虚拟目标点，卫星姿态按照相对轨道坐标系先绕X轴旋转φm实现电扫方向指向r2，再绕与r2垂直方向旋转θm实现电扫方向指向rst。

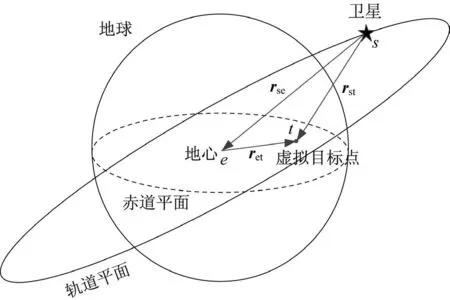
图4 卫星指向虚拟目标示意图Fig.4 Schematic diagram of satellite pointing to a virtual target

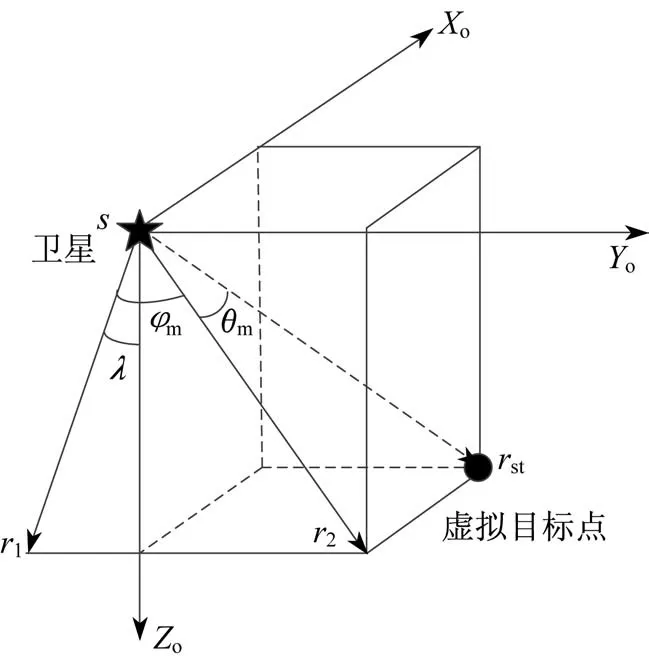
图5 滑动聚束成像基准姿态确定示意图Fig.5 Schematic diagram of reference attitude of sliding bunching imaging

记rst=[rx ry rz]T，两次旋转角度φm和θm分别为

式中：λ为预置的雷达波束扫描角。

采用相对轨道坐标系的四元数描述滑动聚束成像基准姿态可表示为

式中：⊗为四元数乘法。

对四元数按照以下运动学逆方程求取目标姿态角速度ωm：

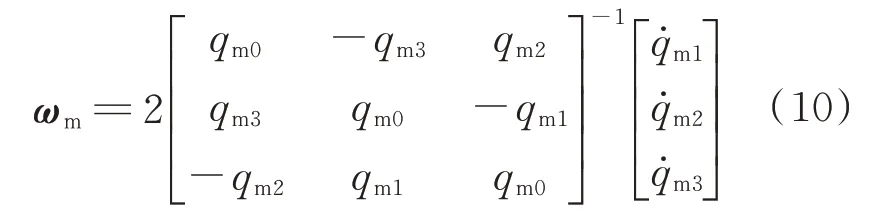
式中 ：为q对时间 的导数，qm=[qm0qm1qm2qm3]T；qm0为四元数标量。

3 控制器设计

定义目标姿态的虚拟动坐标系为“m”系，目标姿态相对轨道坐标系的四元数为qm，星体相对轨道坐标系的四元数为qb，目标姿态相对轨道坐标系的角速度为ωm，星体相对轨道坐标系的角速度在本体系表示为ωb，目标姿态相对轨道坐标系的角加速度为am。除了ωm、am是表示在目标姿态的本体系下外，其他矢量都是表示在卫星本体坐标系下。

姿态四元数误差和姿态角速度误差分别表示为

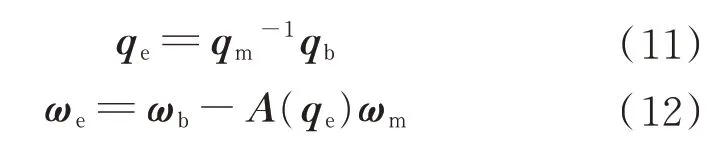
式中：A(qe)为星体姿态相对目标姿态的旋转矩阵；，其 中，qev为qe的矢量部分；ωb=ωs-A(qb)ωo，其中，ωs为星体惯性角速度。

采用基于四元数和姿态角速度反馈的改进型递阶饱和控制算法，控制卫星当前姿态向目标姿态qm趋近，可得反馈控制力矩如下：

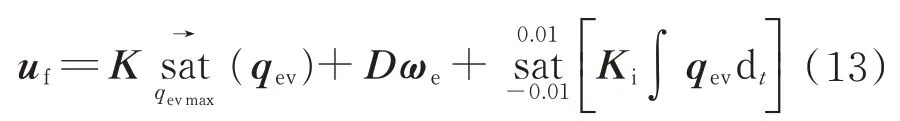
式中：ωe为姿态角速度误差在控制基准坐标系下的表示；qev为误差四元数的矢量部分；K、D、Ki为控制参数常值对角阵；sa（t）为限幅，上标和下标分别对应限幅上限和下限。

qevmax是控制器中四元数偏差的限幅值，采用矢量限幅的方式，即

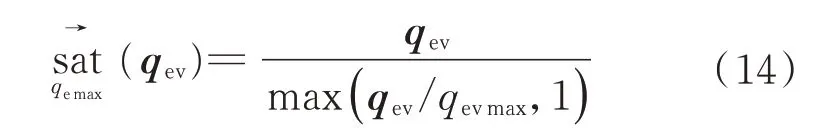
将式（12）代入式（2），得到误差姿态动力学方程为

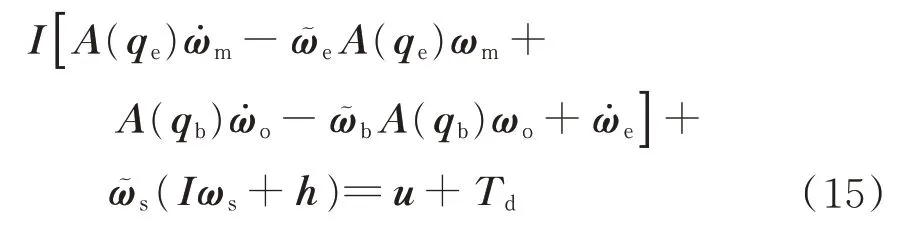
式中：ωs为卫星本体相对惯性系的角速度；hg为控制力矩陀螺群合成角动量；ωo为轨道角速度在轨道系下的表示，近圆轨道ω˙o≈0，椭圆轨道ω˙o通过星上实时计算得到；ω˜为ω的斜对称矩阵。

所以，设计前馈控制力矩为

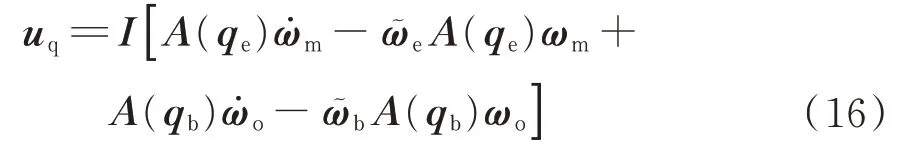
指令控制力矩为

4 仿真试验

以敏捷SAR 卫星的姿态机动控制为例，转动惯量参数见表1。

SGCMG 系统配置5 台10 N·ms 控制力矩陀螺，采用五面锥构型，锥顶角为β=45°，如图6所示。

设置仿真初始姿态[2 2 2 ]°，初始惯性角速度[0.010 -0.050 0.010]（°）/s，0～100 s 卫星处于对地平飞姿态，100 s 后先后机动至前侧视37°状态、平飞状态、后侧视37°状态。仿真中控制力矩陀螺群操纵律采用文献［14］所描述方法，仿真结果如图7～图11 所示。

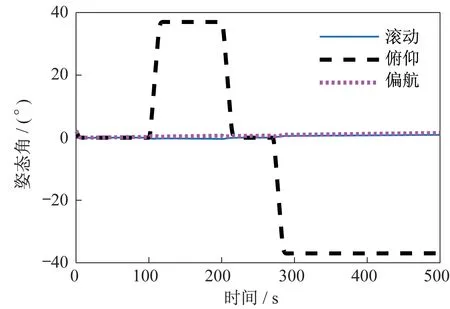
图7 连续机动的姿态角变化Fig.7 Attitude angle of multiple maneuver

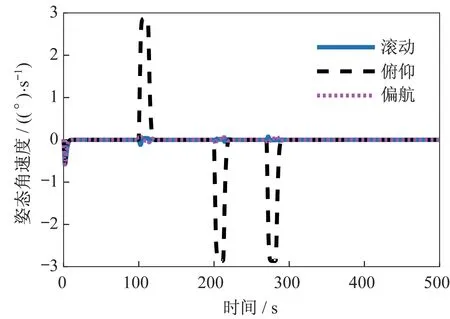
图8 连续机动的姿态角速度变化Fig.8 Attitude angle velocity of multiple maneuver

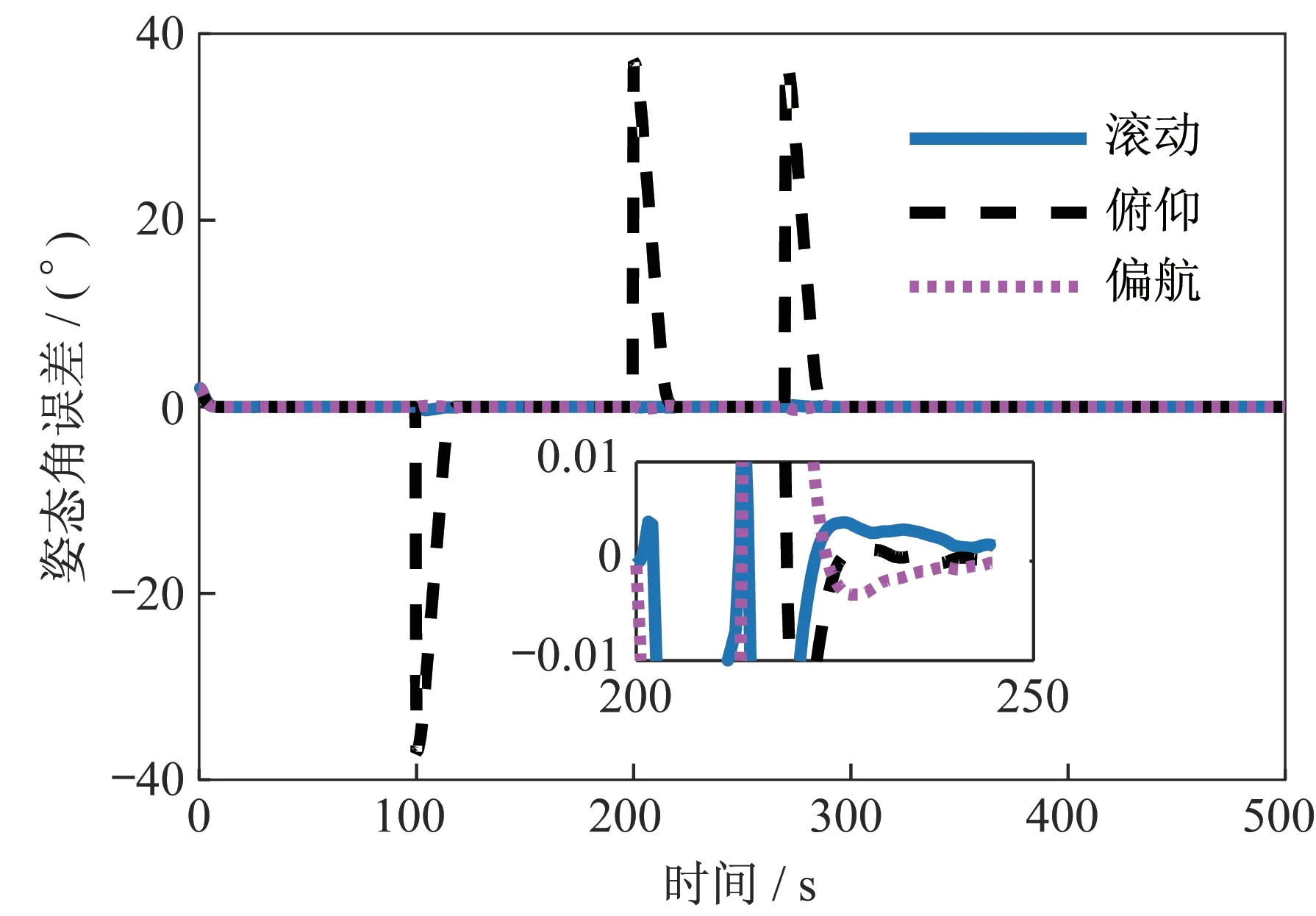
图9 连续机动的姿态角误差Fig.9 Attitude angle error of multiple maneuver

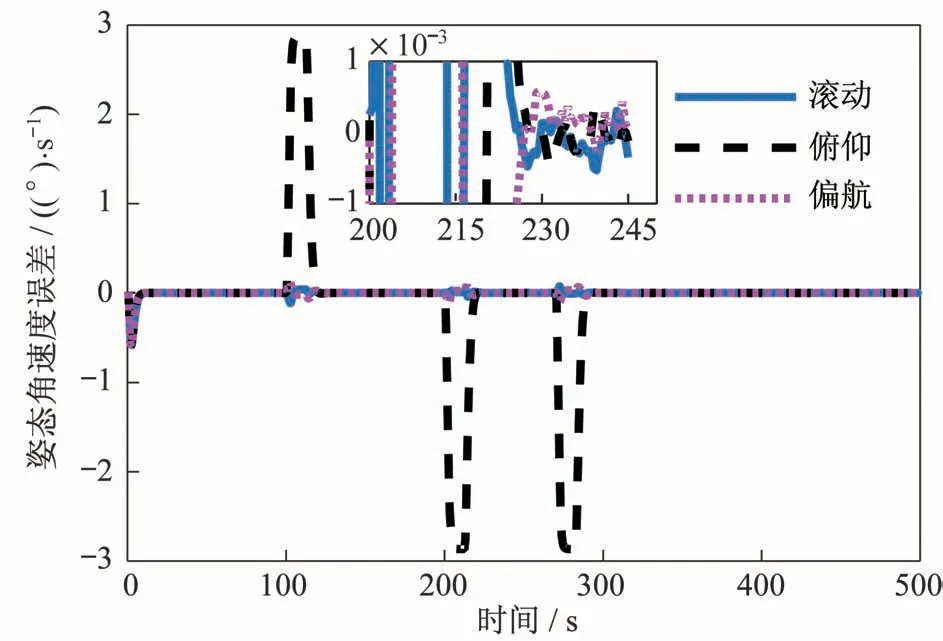
图10 连续机动的姿态角速度误差Fig.10 Attitude angle velocity error of multiple maneuver

图11 连续机动的控制力矩陀螺外框角位置Fig.11 SGCMG frame angle of multiple maneuver

由仿真结果可知，所设计的控制系统在26 s 内绕卫星俯仰轴机动37°并实现0.01°指向精度和0.001（°）/s 稳定度，最大机动角速度为2.800（°）/s。

给定如下虚拟目标见表2，对卫星指向跟踪目标进行仿真。

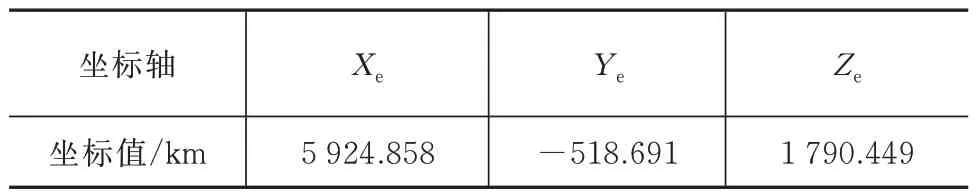
表2 虚拟目标位置Tab.2 Coordinates of the virtual target

仿真初始姿态[2 2 2 ]°，初始惯 性角速 度[0.010 -0.050 0.010 ]（°）/s，平纬度幅角150°，恒星时角102.976°。100 s 开始向指向跟踪基准姿态机动，300 s 滑动聚束成像任务完成，姿态转对地平飞。仿真结果如图12～图17 所示。

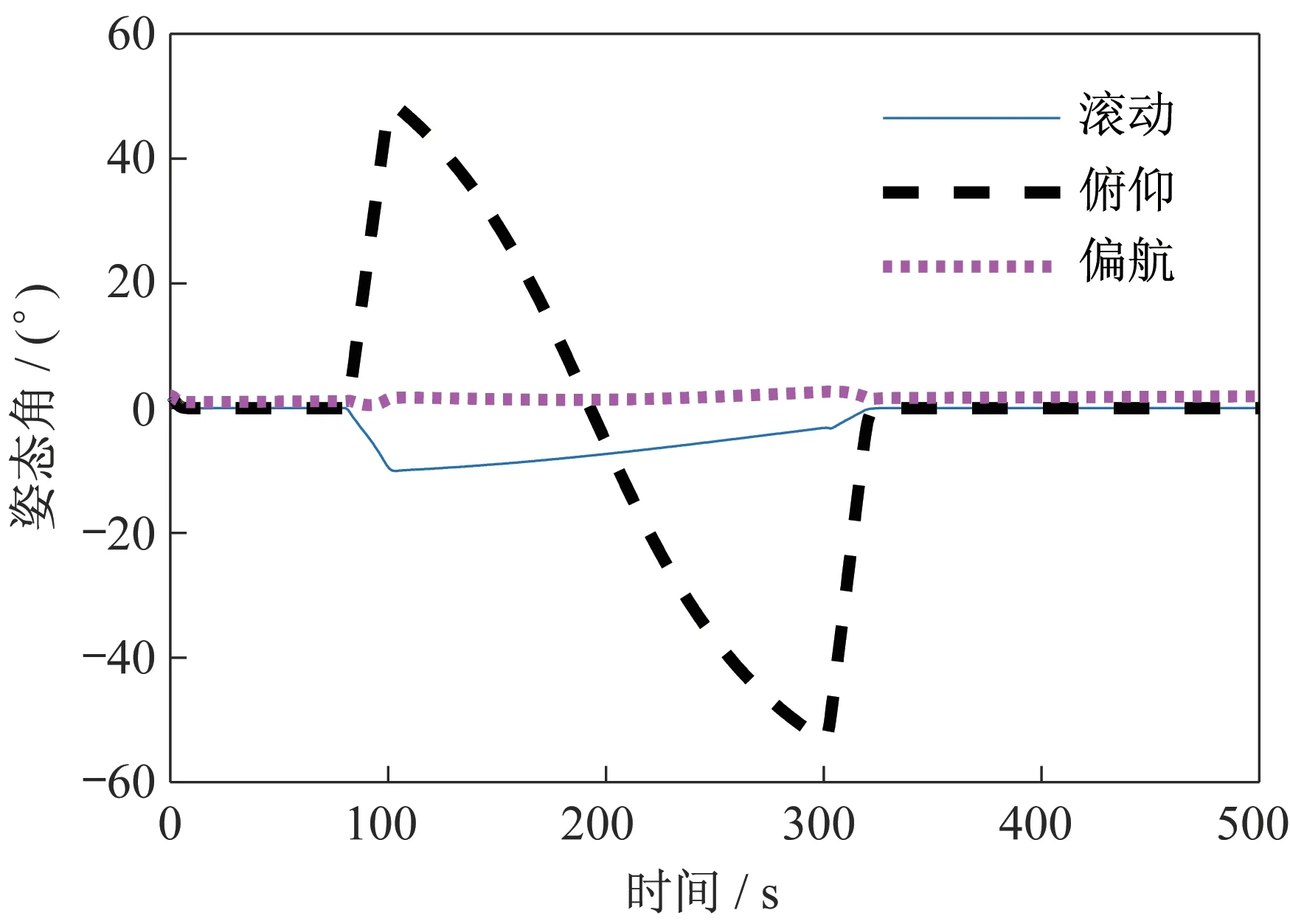
图12 滑动聚束模式姿态角变化Fig.12 Attitude angle of sliding bunching mode

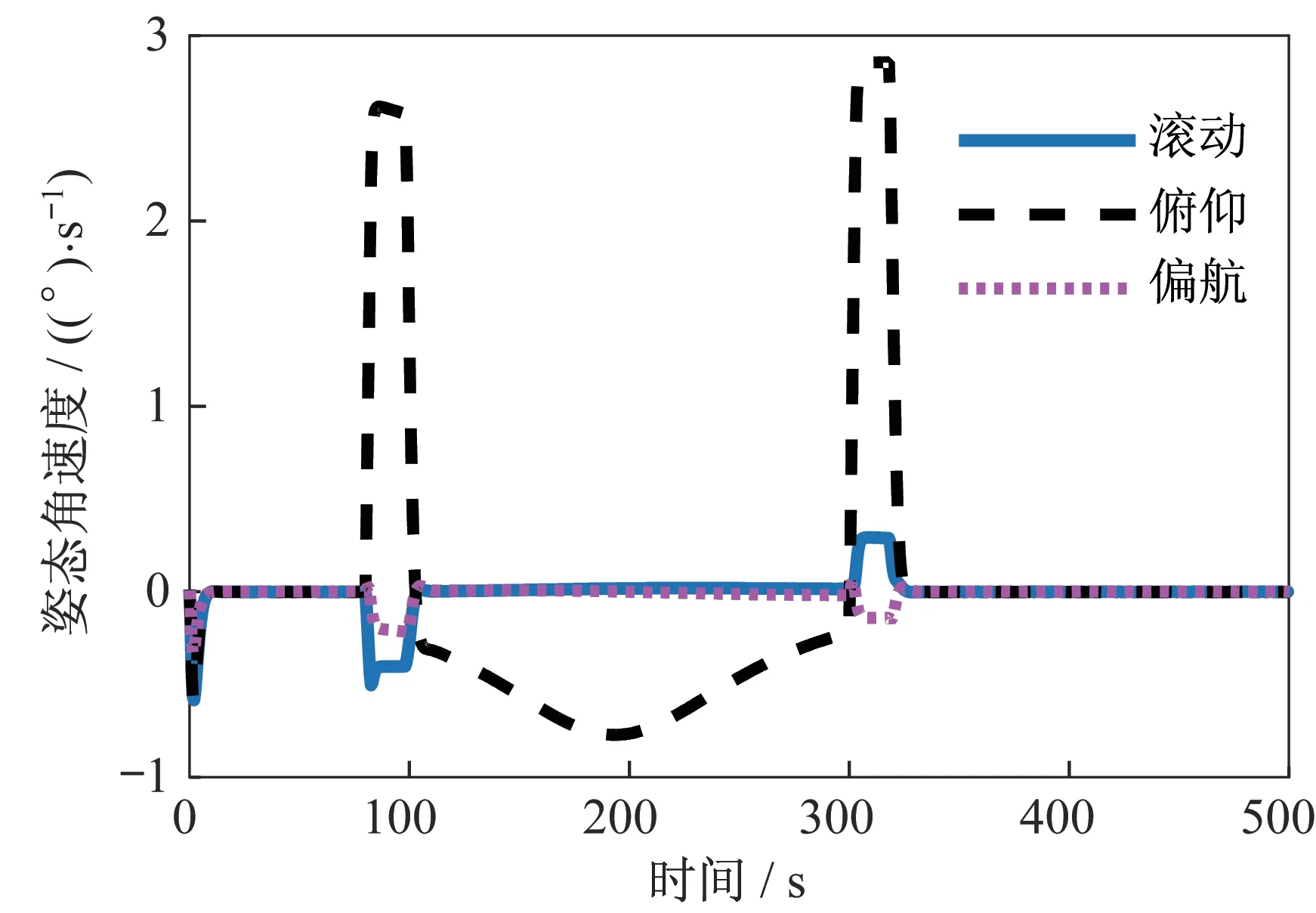
图13 滑动聚束模式姿态角速度变化Fig.13 Attitude angle velocity of sliding bunching mode

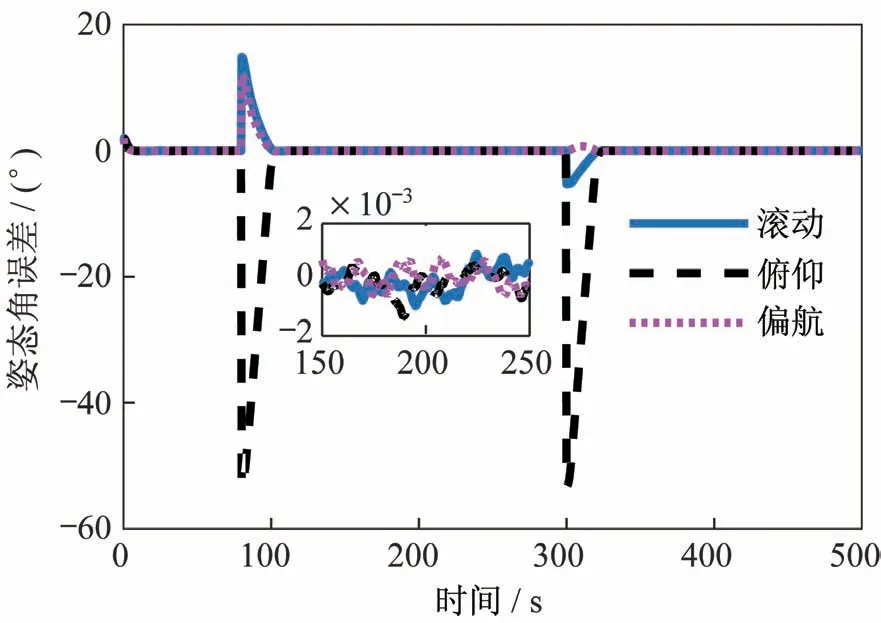
图14 滑动聚束模式的姿态角误差Fig.14 Attitude angle error of sliding bunching mode

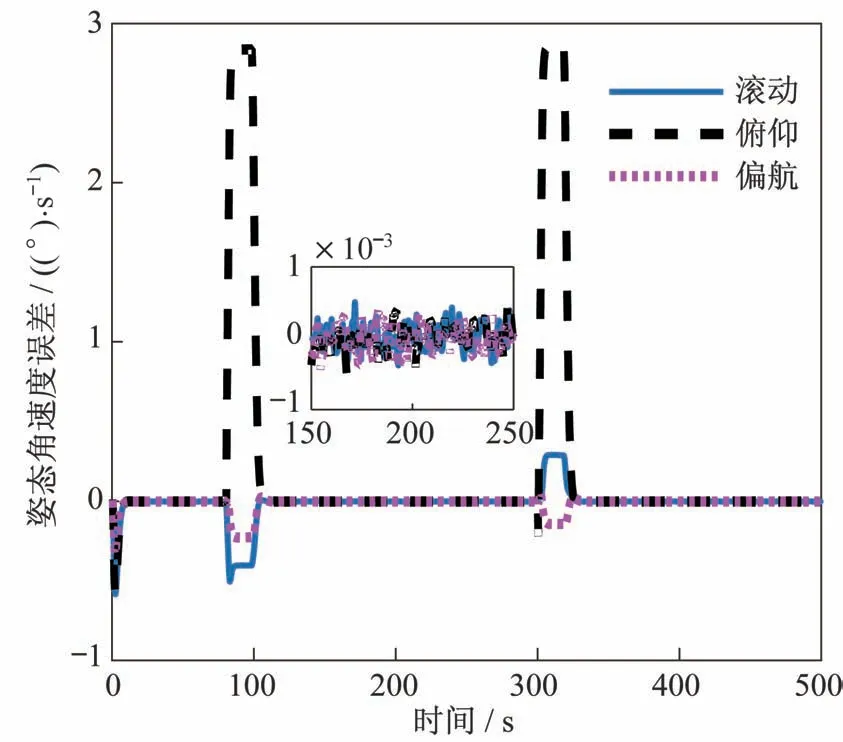
图15 滑动聚束模式的姿态角速度误差Fig.15 Attitude angle velocity error of sliding bunching mode

图16 滑动聚束模式的控制力矩陀螺外框角位置Fig.16 SGCMG frame angle of sliding bunching mode

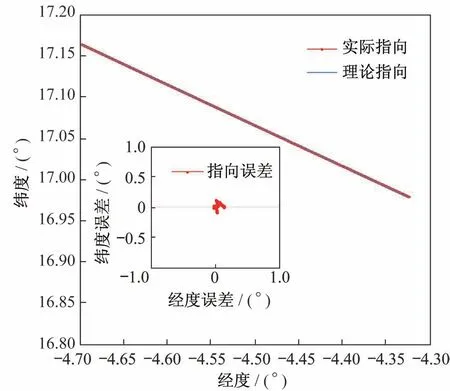
图17 跟踪过程中波束指向在地球表面投影Fig.17 Beam points to a projection on the earth’s surface

由仿真结果可以看出，所设计的控制系统在指向跟踪目标点时，姿态角跟踪精度可达0.002°，姿态角速度跟踪精度可达0.000 7（°）/s，波束中心指向控制偏差优于5 m，实现了SAR 载荷高波束瞄准精度和高成像质量。

5 结束语

传统SAR 卫星为了实现快速响应和高分辨率成像，需要载荷具备二维电波束扫描能力，导致卫星造价昂贵，并且电波束扫描无法实现连续波束角切换。

本文提出使用具备一维电波束扫描能力的SAR 载荷结合卫星平台姿态敏捷机动，实现传统SAR 卫星二维电波束扫描具备的成像功能，并且在雷达波束扫描角固定情况下，通过平台机动可实现连续的波束角切换，提高成像分辨率。针对载荷波束指向捷变扫描与平台姿态敏捷机动一体化控制实现SAR 成像方案，提出了典型成像模式包括条带成像模式、多条带拼接模式和滑动聚束成像模式对姿态的机动需求与跟踪策略；给出基准姿态确定算法，构建基于SGCMG 系统的卫星姿态控制系统，引入基于姿态四元数和角速度反馈的改进型递阶饱和控制算法；实现了卫星大角度敏捷机动和稳定跟踪控制，通过数学仿真结果表明了该控制方案的有效性。