大口径火箭弹模态试验及仿真方法研究

李东旭,郭向向,肖艳文

(1.海装广州局，广州 510000；2.山东特种工业集团有限公司，山东 淄博 255201；3.中国人民解放军32381部队，北京 100071)

1 引言

随着对火箭武器系统的射程、威力需求的不断增加，新型火箭弹的长径比、飞行速度等较以前有很大的提高。对于大长径比火箭弹，飞行过程中弹体对控制力、气动力、发动机推力等外力的响应极大地影响弹体飞行强度及飞行稳定性[1]。大长径比的弹体飞行过程中偶然受到扰动后，就会引起共振，导致飞行失稳，出现掉弹等现象。因此，在大长径比火箭弹结构设计时必须进行动态特性试验，即进行结构动力学的分析计算。为了解火箭弹的动态特性，一般采用模态试验和有限元分析2种方式进行验证，通过仿真计算和模拟试验2种方式，获取火箭弹被动飞行阶段的多阶模态参数、共振频率、模态振型等[3]。由此判断设计的弹体结构是否满足设计上的力学性能要求，后期优化大长径比火箭弹的结构设计，减少由外部激励对于火箭弹飞行造成的影响[2]。本文采用多输入多输出(MIMO)模态识别试验方法验证了有限元分析火箭弹动态特性的准确性，为后期的动态特性分析方法提供依据。

2 基于MIMO的试验及模态辨识方法

2.1 模态分析基本原理

MIMO即多输入多输出模态分析方法，模态分析的基本思想实质上是一种坐标变换，其目的在于把原物体坐标系统中描述的相应向量，转换到“模态坐标系统”中来描述，建立模态试验模型[4]。模态试验就是通过对火箭弹部件或结构的试验数据的分析和处理，寻求其“模态参数”。模态参数识别技术是通过试验的方法，在激励状态下测试火箭弹结构或部件的动态响应特征，再对试验模态进行全面的测试和分析，识别出系统的模态参数，获得结构或部件的动态特性。模态分析是建立在在3个基本假设和一个定理基础之上的[5]：

1)线性假设：假设火箭弹结构的动态特性是线性的，也就是说任何输入组合引起的输出，等于各自输出的组合，其动态特性可以用一组线性二阶微分方程来描述。

2)时不变性假设：即火箭弹结构的动态特性不随时间而变化，因而微分方程的系数是与时间没有关系的常量。确定我们需要的与系统动态特性所有关的全部数据都是可以测量的。

3)确定我们所关心的系统动态特性所需要的全部数据都是可以测量的。

4)Maxwell互易性原理：测试结构应遵从Maxwell互易性原理，即在a点输入激励起的b点的响应，等于在b点的相同输入激励起的a点响应。此假设使得刚度矩阵、质量矩阵、阻尼矩阵和频响函数矩阵都成为对称矩阵[6]。

2.2 弹体MIMO试验方法设计

试验时，将弹体用弹性绳索悬挂在空中，以此来模拟该火箭弹的自由状态。本次模态试验我们采用了多点激励输入多点输出(MIMO)的锤击试验方法。整个弹身上布置3到5个加速度传感器，根据弹的结构特征设置30多个锤击点。每个锤击点敲击3次，采集加速度响应值。移动力锤对每个布置在构件上的测点进行锤击激励的方法采集激励和响应信号，然后在计算机中进行存储记录。每个测点敲击3次是为了防止力锤敲击力度不当带来的误差，3次敲击后取敲击力和加速度的平均值。测试仪器的连接如图1所示。

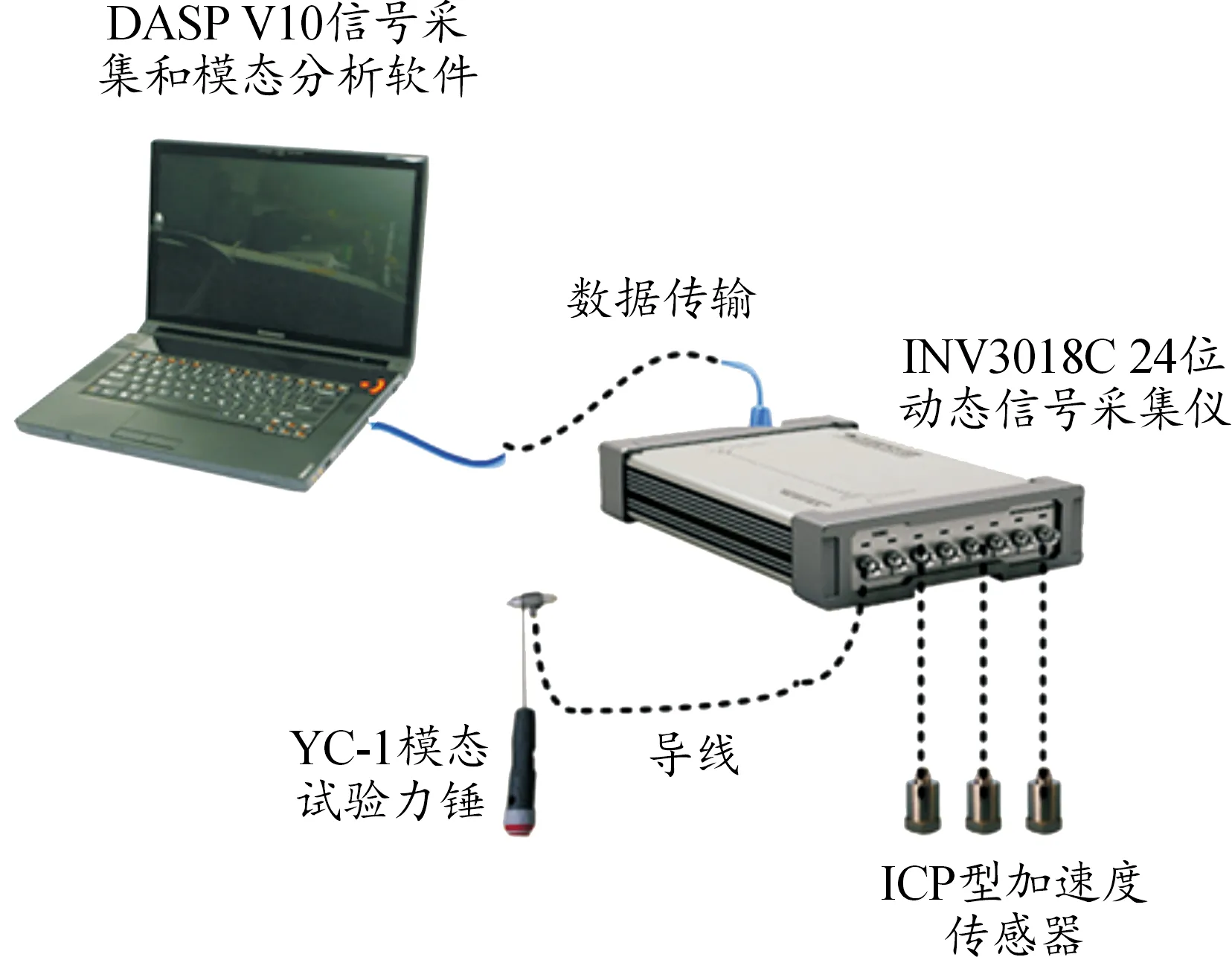
图1 测试仪器连接示意图

以弯曲模态识别为例，模态试验时共布置测量点35个，以弹体最末端记为1号点，依次测量35个点，各测量点的位置如图2所示。

图2 弯曲模态试验各测量点位置示意图

2.3 模态测试结果分析

首先对采集的数据进行传递函数分析，建立模态文件，生成结构模型，输入参考点和测点信息，然后通过特征系统实现算法(ERA)对频率、振型、阻尼等参数进行提取。ERA算法对低频、重根、密集模态有很好的识别能力，图3为特征系统实现算法稳定曲线。

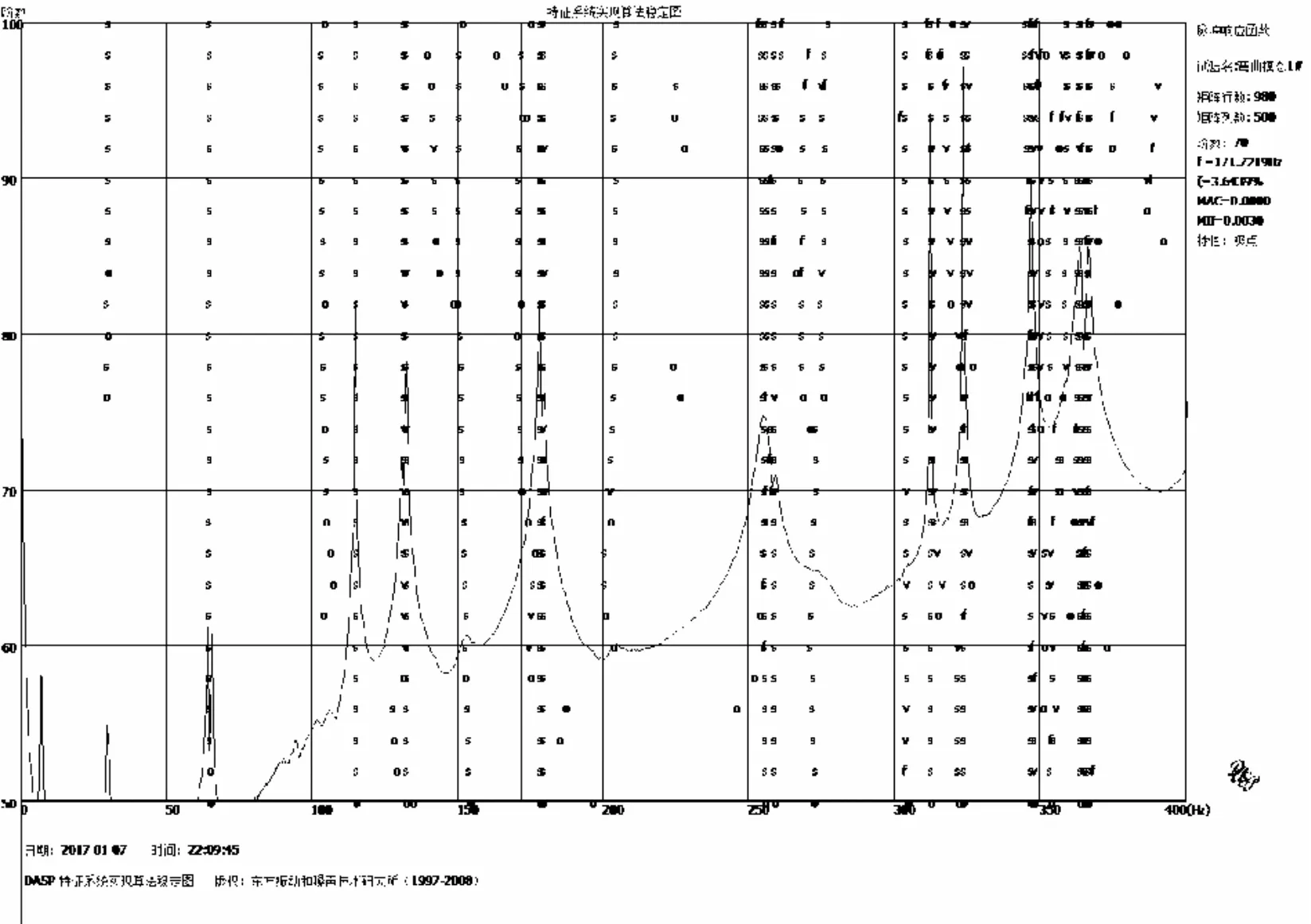
图3 特征系统实现算法稳定曲线

当得到模态分析结果后，采用振型相关矩阵进行校验，检查模态分析的振型结果是否可靠。用振型相关矩阵校验法，进行各阶模态振型之间的正交性校核，矩阵关于主对角线应对称，主对角线的元素都为1。矩阵的行号和列号分别代表两阶模态，其大小表示了这两阶模态振型的正交性，是归一化后的两阶模态振型标量乘积，乘积越小表示正交性越好[7]。如图4所示，弯曲模态的中的一弯和二弯MAC值为0.03，一弯和三弯的MAC值为0.04，小于相关标准0.1的要求，正交性较好。

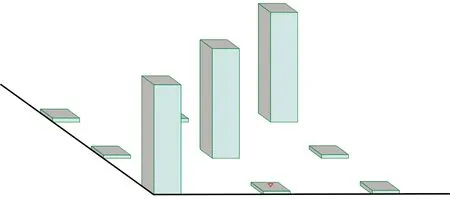
图4 特征系统实现算法稳定直方图

各阶弯曲模态的频率和阻尼试验结果如表1，各阶弯曲模态振型如图5所示，对各阶位移进行归一后得到的振型曲线如图6，弹体不同状态下各测点位移的归一化是将各测点的位移除以该状态下某一测点的最大位移。

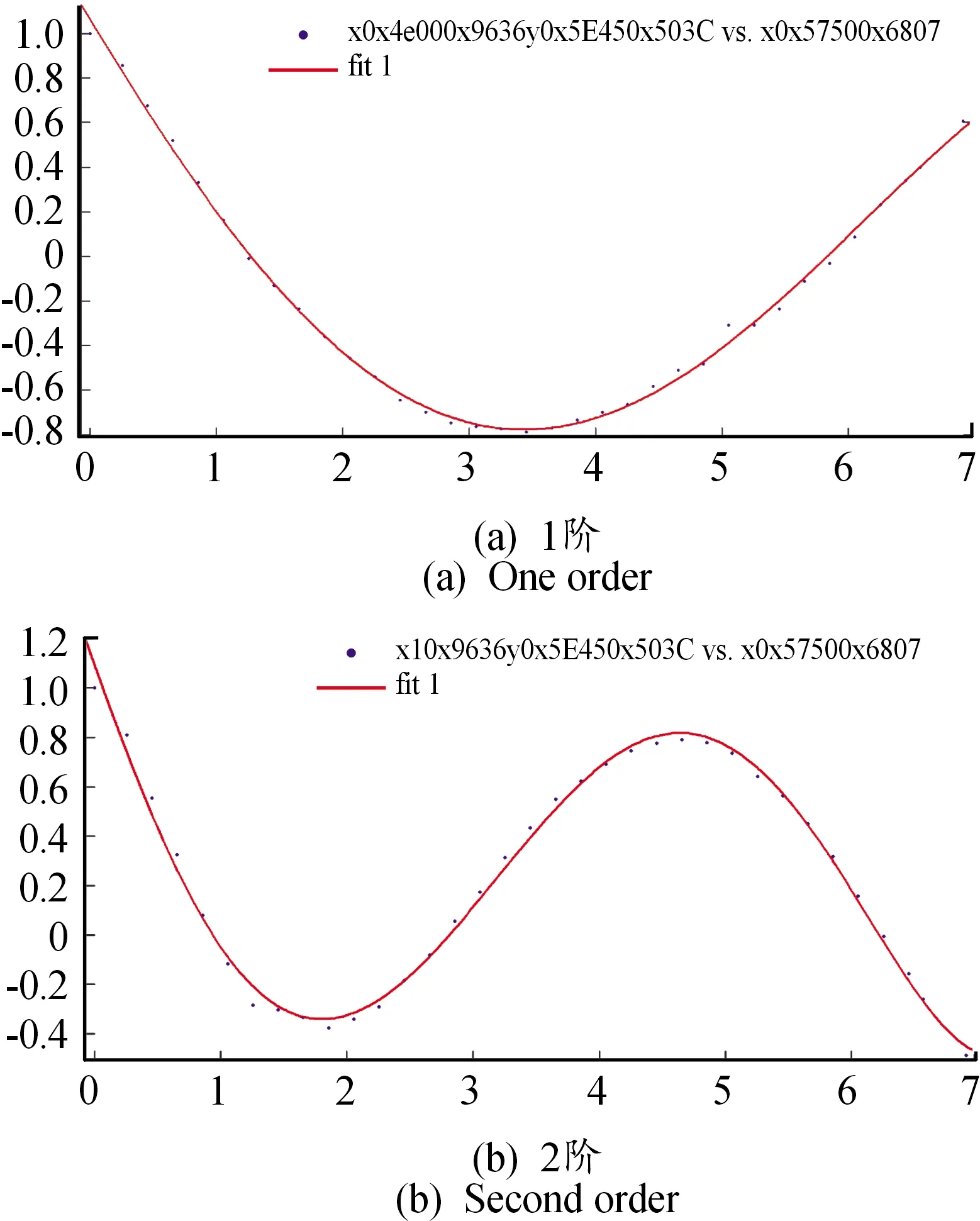
图6 试验模态拟合弯曲振型曲线

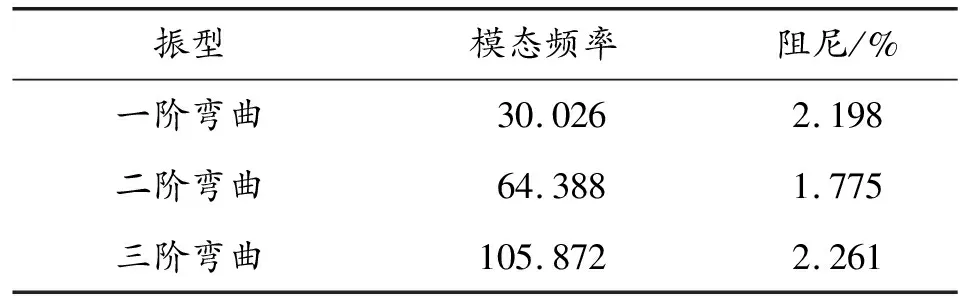
表1 MIMO试验各阶模态试验结果

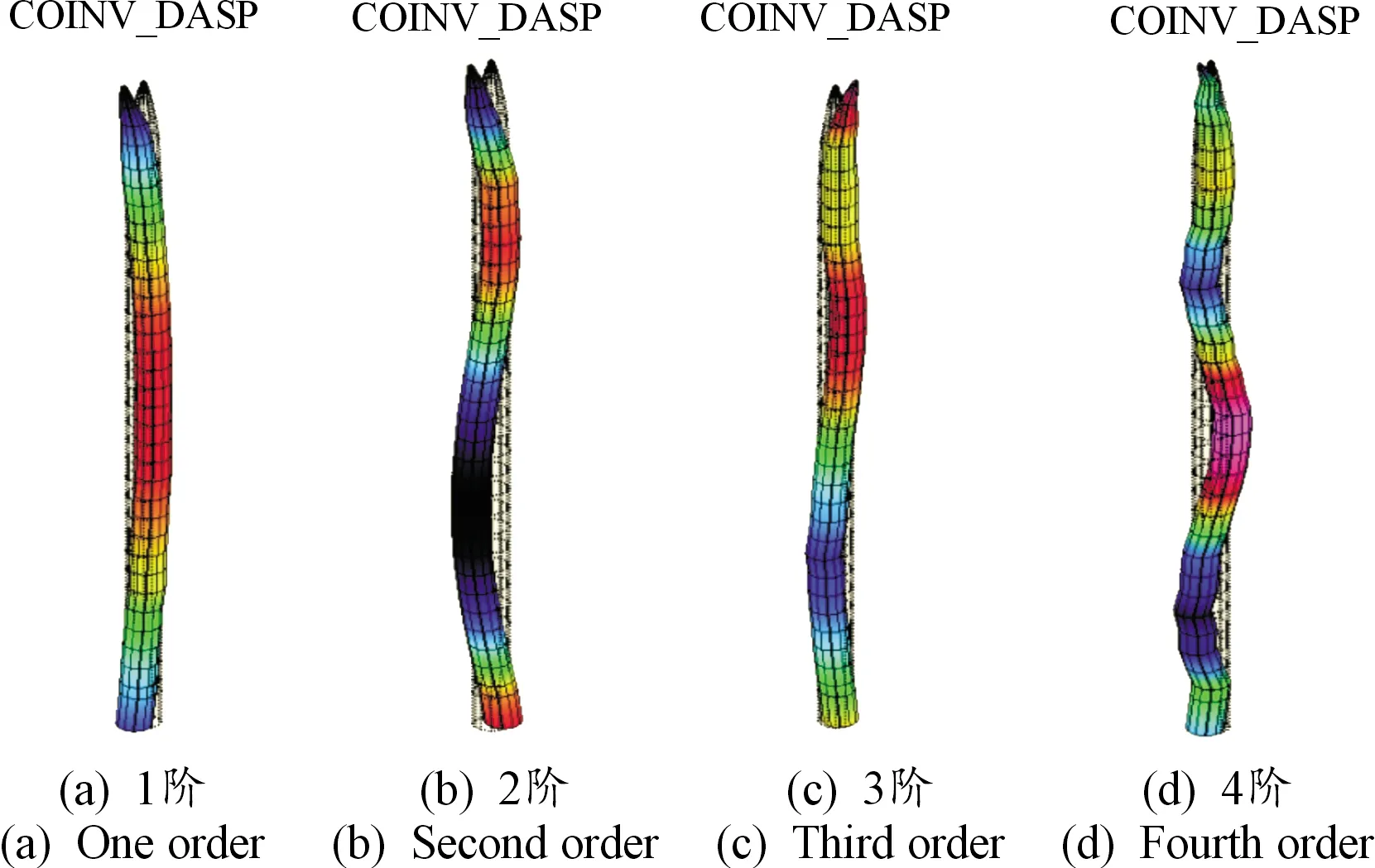
图5 试验各阶弯曲模态振型示意图

3 火箭弹动态特性的有限元数值仿真

采用有限元法进行模态分析是一种研究结构动力特性的新方法[8]。所谓有限元法就是将弹体结构离散化为有限大小、有限数量、具有质量、弹性特性的单元，然后进行数值分析计算，最终得到结构的固有频率和振型[9]。这一方法的巨大优点是在结构设计之初，不需要试制产品样机，根据设计图纸，便可计算出产品的动态性能，并可在设计阶段根据需要进行结构优化，进而消除不利影响，该方法对指导设计具有重要意义[10]。

3.1 结构模型简化

由于火箭弹的长径比非常大，结构非常复杂，实际建模过程中很难考虑到所有的细节。在进行有限元分析时，必须先对整个结构作一些合理的简化，否则会引起计算繁琐，耗费机时[11]。简化工作主要是用壳体的假密度模拟仪器舱、控制舱及燃烧室的内部结构和舵机、尾翼的弹体外部结构。这样，既能大大降低模型的复杂度和计算机时，又能保证足够的计算精度[12]。简化模型如图7所示。按实际结构和材料的不同，把全弹大体分为五部分：头部、仪器舱、控制舱、燃烧室和尾部。对火箭弹各零部件进行质量等效，同时根据结构尺寸进行实体建模求得其理论体积，根据其等效质量求得理论等效密度，再采用大型有限元分析软件计算无约束状态下全弹模态变化[13]。

图7 火箭弹简化模型示意图

3.2 数值仿真模型的建立

弯曲模态共测量同MIMO试验一样共布置35个点，弹尾最末端记为1号点，依次测量共35个点，测量点布局如图2。

根据实际情况对火箭弹各部分材料参数进行假设[14]：头部材料为聚四氟乙烯(PTFE)，其泊松比u=0.4，弹性模量E=0.28 GPa；仪器舱材料为玻璃钢(FRP)，其泊松比u=0.25，弹性模量E=21 GPa；头部体积及质量较小，把头部和仪器舱一起考虑，其参数假设为：泊松比u=0.3，弹性模量E=21 GPa。控制舱、燃烧室、尾部材料均假设为钢：泊松比u=0.3，弹性模量E=210 GPa，密度取其等效质量与体积所得出的理论值，表2为被动段各部分结构等效质量特性。

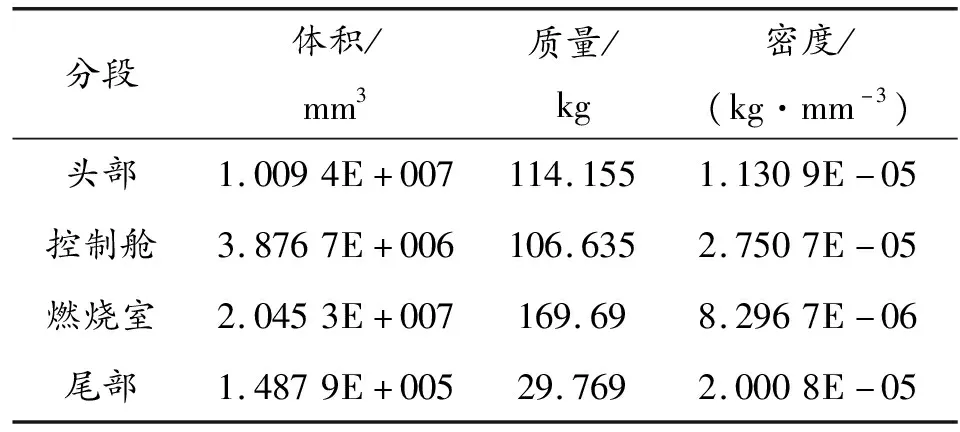
表2 被动段各部分结构等效质量特性

建立有限元模型单元数：2 294 184，节点数：5 003 127，有限元网格模型如图8所示。

图8 全弹被动段有限元模型示意图

3.3 数值分析及结果

经过数值仿真后得到火箭弹的模态频率、模态质量、刚度、阻尼系数及阻尼比见表3，各阶弯曲模态振型如图9所示，各阶位移进行归一后得到的振型曲线见图10。

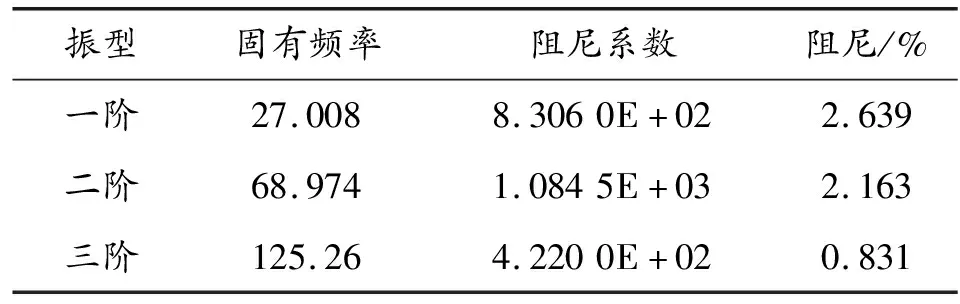
表3 各阶振型固有频率、阻尼系数及阻尼等参数

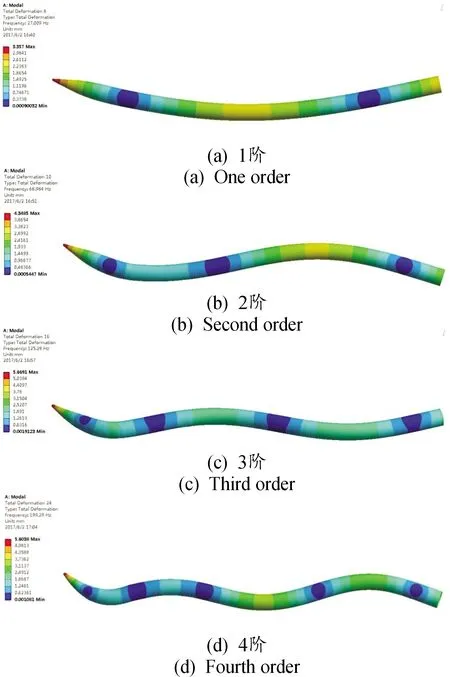
图9 仿真计算各阶弯曲模态振型示意图

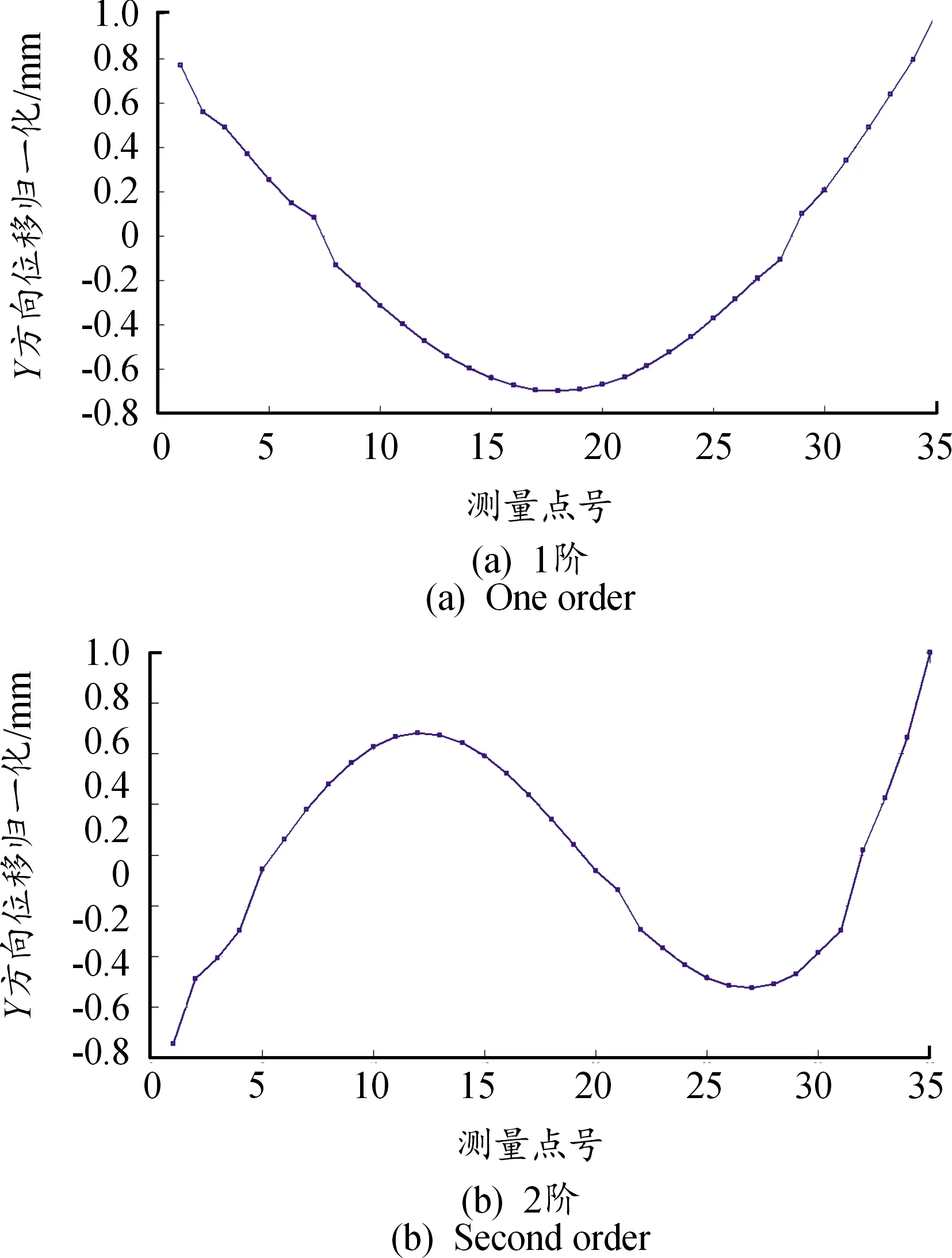
图10 仿真弯曲模态振型拟合曲线

4 2种试验方案结果

弹体前两弯的动态特性最为关键，将前两弯的仿真频率与试验所得频率进行对比可得，MIMO试验得到一弯频率为30.026、二弯为64.388，有限元仿真的到一弯频率为27.008、二弯为68.974。一弯误差为10%、二弯误差为7%，误差在10%以内，符合设计要求，具体结果见表4。

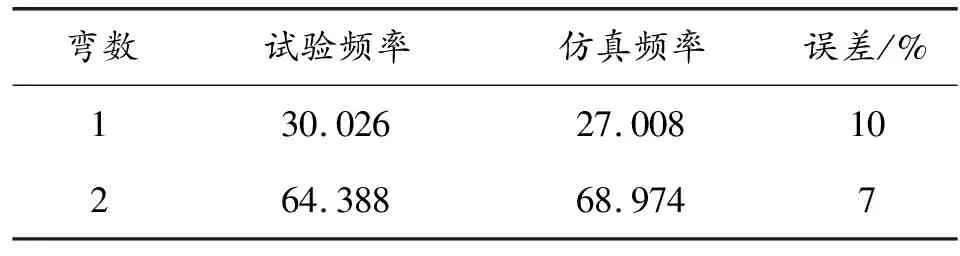
表4 被动段仿真频率与试验频率

弹体不同状态下各测点位移的归一化后的振型曲线如图11，由图可以看出2种试验条件下的位移归一曲线特别接近，有些区域为重合状态，误差很小。因此有限元仿真满足动态特性试验的要求。

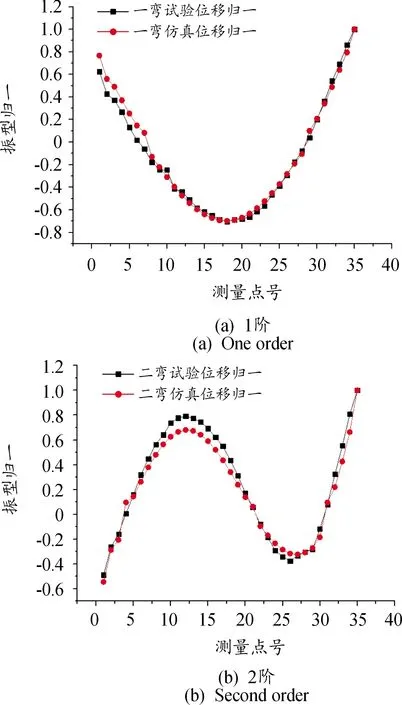
图11 仿真试验弯曲振型曲线

5 结论

通过MIMO即多输入多输出模态分析方法和有限元分析方法，对大长径比火箭弹进行动态特性试验，得到前四阶弯曲的弯曲模态振型曲线、频率、阻尼以及归一化后的振型曲线。2种试验时在各阶的弯曲模态振型曲线一致，对本试验来说前两阶弯曲的影响比较大，第一和第二阶弯曲的频率误差小于10%，2种试验条件下的前两阶弯曲位移归一曲线特别接近，有些区域为重合状态，误差很小。动态特性试验的结果与有限元仿真结果一致，火箭弹后期科研阶段可采取这种经济、省时的仿真试验方法，在设计阶段根据需要改变结构的形状以消除不利影响，该方法对指导火箭弹设计具有重要意义。