以画促思,以图求解
马苏婉


【摘 要】小学低年段学生的思维主要以具象思维为主,对稍复杂问题的理解与消化能力较弱。在解决问题教学中,教师要善于引导学生借助几何直观,把抽象的问题简单化、直观化,找到解决问题的突破口,架起学生行与思的桥梁,提高低年段学生解决问题的能力。
【关键词】几何直观 低年段 解决问题
所谓几何直观,主要是指借助图形分析来解决问题。几何即是图形,包含点子图、线段图等。图形是数学直观化的语言,利用图形发现问题中的关系,从而帮助我们化难为易,找到解决问题的方法;直观是对图形表象特征的感知,通过图形洞察事物的本质,从而发现规律。借助几何直观解决数学问题是小学低年段学生常用的一种手段,在数学解题过程中有着重要的地位和意义。
从小学一年级开始,解决问题就在数学教材中占据着重要的地位,它既是教学的重点,也是教学的难点。现行的苏教版一、二年级教材解决问题的题目类型虽经常辅以形象的实物图或情境图表达数学内容,但是也穿插着一些抽象的文字描述,与小学生认知水平有差距,从而成为低年段学生学习数学道路上的“拦路虎”。教师应巧妙借助几何直观训练学生动手画图,层层深入,分阶段实施画图训练,加强画图的系统性学习,从而提高学生的几何直观能力。
一、初试几何直观,画简图知概念
低年段学生最先接触“数”的概念,教师要以此为切入点,逐步渗透,教会学生学会将实物图符号化。学生经历将情境实物图抽象成直观图,再抽象到数的过程,实现“实物图→几何直观图→数”的转化,为学生今后理解、分析题目中的数量关系打下基础。
【案例1】苏教版一年级上册第27页的例题1“1~5的认识”(如图1),教师出示情境图,让学生先数一数,然后用点子图来画一画,最后抽象出数。
在整个教学过程中,通过画一画建立数感、符号感是重要目标之一。因为在第一课时“数一数”中学生已初步认识点子图,教师要有意识地引导学生用点子图来表示这些物体,进一步体会复杂问题简单化的数学思想。
纵观整个“数”概念教学过程,教师引导学生通过几何直观来表示1~5这些数字,用图画式来沟通实物图与数两者之间的聯系,完善“数”概念的教学。久而久之,学生也就慢慢感受到几何直观的好处,培养画图意识。
二、细品几何直观,画算式明意义
低年段学生对加减乘除运算意义的理解程度直接关系到他们日后利用数学知识解决问题的能力。许多学生在解决实际问题时,经常是看到数字直接运算,而忽略了分析题意这一环节。究其原因,主要有两点:一是低年段学生认知能力较弱,没有从根源上理解算式的含义;二是教师没有有意识地引导学生画几何直观图理解分析题意,学生未形成画图的好习惯。
1.“式”由图“生”,探究本源
在之前由实物图抽象出点子图的基础上,教师可以引导学生尝试将图与图之间进行整合,理清其中关系,再用算式表示,完成“点子图→关系图→算式”的有效推进,帮助学生深刻理解算式的由来,明白图形与算式之间的内在联系。
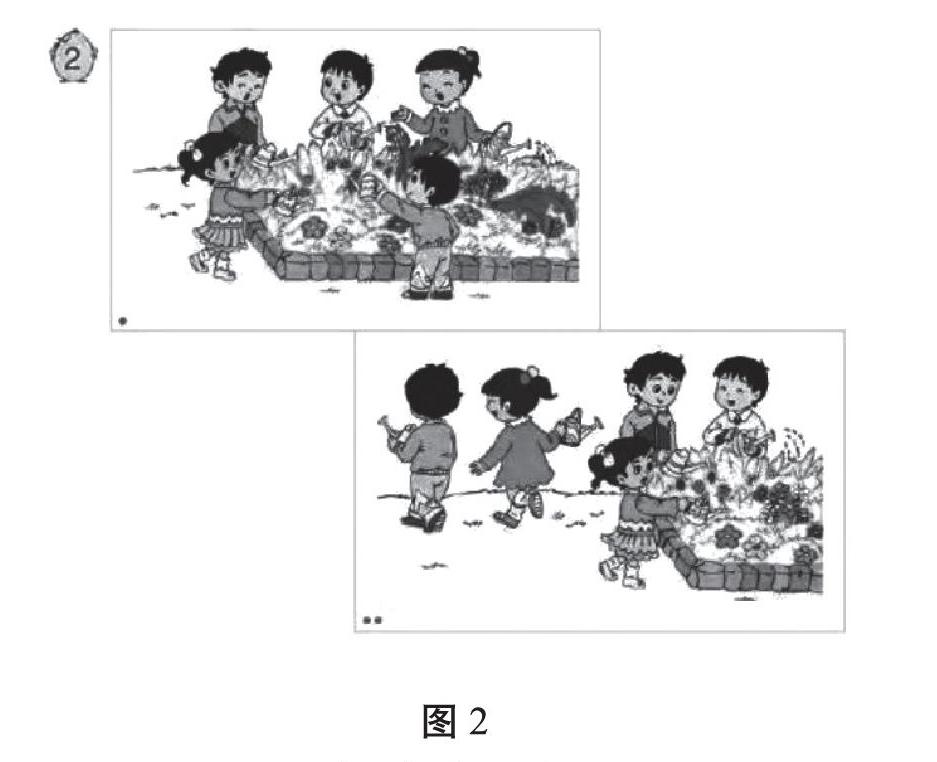
【案例2】苏教版一年级上册第46页例题2“5以内的减法”(如图2)。
这类问题虽然较简单,但在实际教学中有学生列式却是这样的:5-3=2。怎样让学生自己发现错误呢?在学生列出此算式后,教师可以提问:“你能试着用图把题目中的意思画出来吗?”此时,学生根据情境图画出题意(如图3)。
生1:
生2:
生3:
从图3中可以发现,学生能用简单的直观图画出题目的意思,并用画线的方式表示走掉的人数,没画线的则表示剩下的人数,理清单一图形之间的关系。教师要在此基础上,引领学生建构减法模型(如图4),加深对其意义的理解。
通过这一系列的操作,学生很清楚地明白为什么应该列成5-2=3这一算式,就不会出现把问题的答案写在算式中这样的情况。
2.“图”现式“清”,理解含义
画图可以帮助学生区分差异、理解意义,并根据四则运算的具体含义选择正确的运算方法,
例如,在教学苏教版二年级下册第21页的例2后,学生对于乘法的含义有了一定的认识,但是对于画图思想印象不深,还需设计题目充实,通过图真正理解算式含义。设计出示2×5,让学生独立画图来表示此算式。有的学生画圆形来表示,有的学生画正方形来表示,有的学生画三角形来表示;有的人画3个6,有的人画6个3。此时让学生看图说一说“算式中的3表示什么?6又表示什么?你能编一道题用此算式解答吗?”,学生利用画图,把文字符号转变为图形,由抽象回到直观,深刻理解乘法的意义,帮助学生进一步感受到画图的好处。
当学生经常自主探究算式的由来,经常将文字转换为图形来理解算式含义,几何直观图在学生面前出现的次数达到一定程度时,一旦遇到稍微有难度的问题,学生就会第一时间想到画几何直观图,以帮助其理解意思,解决问题。
三、知味几何直观,画数量显关系
解决问题教学最能体现学生的几何直观训练成效,其考查的是学生理清题目中数量关系的能力,借助几何直观策略展示所要表达的信息,化难为易,进而分析数量关系,探索解决问题的方法。
1.善用线段图,简化数量关系
随着年级的升高,知识量不断增多,问题中的数量越来越多,数量关系也越来越复杂,不可能用符号一一表示出来,这时,可以借助线段图来分析数量关系。但是线段图在中高年级才会学习,低年级教学并未涉及线段图。那么如何在低年级教学中逐步渗透画线段图的意识与方法呢?
例如,在苏教版二年级上册教材中,教学“把两个大小不同的数量摆成同样多的问题”,习题中已出现以长方形的长短来表示数据的大小。因此,在教学例题时,很有必要将例题延伸,以引发学生的思维碰撞,从而逐步引出线段图的雏形。
【案例3】 苏教版二年级上册第6页例题3(如图5)。
(1)画图:小軍有8个彩珠,用8个红色圆片来表示;芳芳有12个彩珠,用12个蓝色圆片来表示。
(2)分析:让学生说一说,芳芳比小军穿的是哪一部分?
(3)变形:若用这个长方形表示小军穿的个数(长方形遮住圆片),那么这个长方形表示多少?(8个)同样,用一个长方形遮住芳芳穿的个数,那么这个长方形又表示多少呢?(12个)。你能指出哪一部分是芳芳比小军多的吗?形成如6图所示:
(4)理解:两个长方形各表示什么?各表示多少?
(5)练习:出示习题——苏教版二年级上册教材第7页看图填空(如图7)。
(6)对比:你觉得哪种画图方式比较好?
从点子图到色条图的过程,是学生认识线段图的一大跨越。学生通过画线段图的雏形将抽象的问题直观化,化繁为简,从而突破思维的瓶颈,提高解题的挑战性。
线段图雏形建立后,到二年级后续学习线段就可以直接将色条图简化成用线段表示,帮助学生建构完整的线段图体系,为中高年级学习线段图打下基础。
2.借用示意图,分析数量关系
当学生单从读题不能清晰地分析出题目中的数量关系时,教师要引导学生借助几何直观还原出题目的原始脉络,通过观察、思考来解决问题。
例如,二年级下册有一道习题:水果店有一批桃子,第一天卖出一半,第二天卖出剩下的一半,这时水果店里还剩下5个桃子。水果店原来共有多少个桃子?
学生读题结束,有的抓耳挠腮,有的一脸茫然。这时教师可以适当引导学生:“你能把这道题的意思用图画出来吗?也许你会打开新的思路。”于是学生开始在纸上涂一涂、画一画,只听见“哦”“原来这样”“我会了”的声音此起彼伏。
通过画图(如图8),学生很快就找到了题目中的数量关系,并列出算式,甚至有的学生还能够借助所画的图,生动有趣地讲解题目的解决方法,自由地阐述自己的思维过程和结果。同样一道题,学生运用了不同的几何直观图,展现了不同的思维品质。学生已经能够选择个性化的图形进行画图分析,这是学生思维的真实展现。
生1:
生2:
生3:
生4:
教师应将学生的成果展示给全班同学,对他们进行充分的鼓励和肯定,并可适当引导学生发现其内在联系,优化几何直观图的画法。通过坚持这样长期的训练与比较,画图一定会成为学生的一种良好学习习惯。
几何直观训练在我们的教学实践中已有成效,经过两学年的努力,学生解决问题的能力进一步提升,碰到稍复杂的问题就会自然而然地想到用画图的方法解决,多数学生已经能自如地以图促思、以图求解,体会“画图方法”的优越性,轻松实现文图转换,提升解题有效性。
总之,在小学数学解决问题的教学中,几何直观的策略运用无疑给学生提供了更多的思路和解题方法,有助于学生更准确地接受新的知识,突破重难点,正确理解数量关系,提高解决问题的能力。因此,教师应将几何直观训练贯穿于整个小学数学教学中,特别是在低年段,要不断引导学生体会几何直观的价值和作用,使他们养成画图的好习惯。

