直墙前多向不规则波波高平面分布的数值模拟研究

罗天翔，朱良生*，徐润刚，程赵德

（1.华南理工大学土木与交通学院，广东 广州 510640；2.中交第四航务工程勘察设计院有限公司，广东 广州 510230）

0 引言

由于离岸建筑物的布置在港湾工程的重要性逐渐提高，如今工程设计不仅关注波要素对直墙的作用，对于直墙前沿水域的波高平面分布也要有全面的了解，以便能够合理地确定直墙前沿的泊位、浮码头等工程布置位置。实际波浪往往是不规则且方向不单一的，多向不规则波更符合天然波浪的特性。因此研究正向、斜向入射后的多向不规则波经历反射、叠加作用后波浪在直墙建筑物前沿水域的平面空间分布具有重要意义。

陈汉宝[1]使用数值模拟和物理模型探讨了斜向波与直立式防波堤的相互作用，波高最大值与斜角的关系，给出了对应的波态图，定性分析了波浪特性；冯卫兵等[2]利用浅水定常莆田经验谱分解结果等模拟非线性随机波在直墙前的运动和动力过程，形成了波高、周期等一系列极值序列、分布曲线，但二阶非线性理论解不能完全表现近岸波浪的非线性，对波高等要素的统计分布停留在直墙上的概率分布；俞聿修等[3]探讨了波浪斜向性和多向性对不规则波作用于直墙堤上波浪荷载的影响，并提出了实用的计算方法；骆俊彬等[4]采用物理模型试验证明不规则波作用下的直墙前的波谷压力概率分布可以用韦伯分布来描述，并与相对波高有关；姚国权等[5]在从堤头多角度入射的波况下研究了规则波与不规则波反射问题，推导了规则波沿直立堤外侧波高分布的计算式，沿直立堤方向横截面的不规则波和规则波的波高分布，这里未强调波浪的非线性；周枝荣等[6]结合物理试验和相关研究成果，提出斜向波作用在矩形重力墩结构上最大总水平波浪力简化计算公式；张文海等[7]分析了统一方程，并以此为基础建立了从深水到浅水域都有效的数值模型。刘思等[8]首先根据给定的波要素、群性参数和方向分布参数，给出了多向不规则波群的数值模拟方法，在此基础上利用有限元法求解改进的Boussinesq 方程的数值计算模型，建立了数值水池在指定位置模拟所要求群性的多向不规则波入射波浪边界条件的计算方法。栾英妮[9]采用Mike21 BW 数学模型，并选用文献[10]中的计算模型进行计算并与其提供的试验结果比较，分析结果表明，Mike21 BW 数学模型与前人试验结果相近，适用于非线性较强、浅水以及有限水深情况下的计算；张娜等[11]使用Mike21 BW 数学模型对波浪在缓坡上的破碎现象及爬坡过程进行了精确模拟，并将此方法成功应用于实际工程中。

关于波浪传播入射后直墙前波高分布的研究，国内外学者已对其进行了大量的理论推算、物理模型以及数值模拟，并得到有效的计算方法和经验公式。但前人的研究多考虑于直墙上波浪力、反射系数，对波高分布的研究讨论集中在直墙与波浪交汇处以及沿堤方向的横切面，相比前人的研究，本文完全考虑不规则波的多向性、非线性，且对直墙前整体水域平面的波高分布以及波长和腹点、节点位置、间距的关系进行了较系统研究。本研究采用基于Boussinesq 方程的Mike21 BW 模型，对正向、斜向入射的多向不规则波在直墙前的反射、叠加过程进行数值模拟，探讨入射波与直墙前有效波高的平面空间分布关系，不同波况的有效波高分布以及得到腹点、节点间距和位置与入射波波长的关系。

1 试验研究方法

1.1 Mike21 BW 数学模型简介

计算采用丹麦DHI 的Mike21 中的BW 波浪模型，该模型通过求解沿垂向积分的Boussinesq方程获得沿水深的平均流速、水位变化以及波高等物理量。模型中考虑了波浪的折射、绕射、反射、底部损耗等因素，可以很好地满足计算内容的要求。对方程采用ADI（交替方向法）算法，式中各项保证二阶精度。新形式的Boussinesq 方程改进了色散关系式，使BW 模型适合模拟从深水到浅水的传播。

1.2 基本方程

式中：x、y 为水平坐标，m；t 为时间，s；ξ 为高出平均水位的水面高度，m；p、q 分别为x、y 方向的流量密度；h 为水深，m；D 为平均水深，m；c为谢才阻力系数，c=M·h1/6，m0.5/s；M 为曼宁系数，m1/3/s；E 为紊动“涡黏”系数；g 为重力加速度，g=9.81 m/s2。

1.3 方向谱

模型中，本文关于方向谱的设置包括对主波向的定义、方向谱的形式以及具体传播参数的设置，波浪频谱选择Jonswap 谱：

式中：f 为波频；f0为谱峰频率，s-1；γ 为谱峰尖度因子；H1/3为有效波高，m；T0为平均周期，s；β为峰型参数；α 为γ 的函数。方向分布类型选择频率相关分布，方向分布函数G（θ）具体表现形式为：

式中：s 为频率相关形状参数；θmain为主波向，（°）。具体传播参数设置为主波向θmain，最大偏离角度Δθmax两项，为了简化试验，本文中Δθmax固定为常用值30°。

1.4 计算实例

1.4.1 试验概况及计算条件

计算水域尺度为1 000 m×7 000 m，水深8 m。造波线距离左侧边界200 m，左、上、下侧边界分别设置海绵层，右侧边界设置为直立实体结构，具体布置情况如图1 所示。本文数值计算多向不规则波经直立实体结构全反射后全水域波浪的水平分布，各计算工况条件见表1，其中主波向角度θmain指波浪的主波向与造波线法向的夹角。

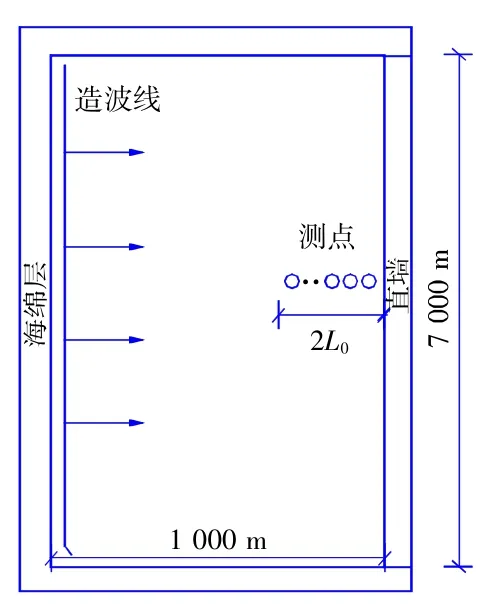
图1 试验地形示意图Fig.1 Schematic diagram of experimental topography

表1 波浪初始入射条件Table 1 Initial wave incident conditions

1.4.2 模型设置

采用矩形网格划分，空间步长Δx=Δy=1 m，时间步长Δt=0.1 s。近岸采用直立实体结构，反射系数为1，模型四周在开边界上设置海绵层，吸收超出模型范围的波浪，造波线后面产生的波浪也被置于该处的海绵层吸收。

试验造波方式选择多向不规则波，Jonswap 谱参数的谱峰尖度因子γ=3.3，σa=0.07，σb=0.09。取稳定后200 个左右波的实时波面数据进行统计分析，测点间距1 m，采取的测点与直墙的最远距离为入射波的2 倍深水波长，造波线设置在距离左、上以及下边界200 m 处，依据模型的计算要求，最小周期（截断周期）设置为0.7 s。

消波系数按式（6）计算：

式中：α 和r 为给定的常数；Nsponge为消波线的数量。海绵层的宽度一般为波长的1～2 倍。

2 数学模型验证

选取Demirbilek 和Nwogu 的物模试验工况对数学模型进行对比、验证。模型布置见图2。试验从造波端至右侧斜坡边界一共布置9 个波高仪，造波端左侧布置的海绵层厚度为5 m，右侧斜坡边界的坡度为1∶12。波浪在深水区经历一段等水深传播至由3 段斜坡组成的复合斜坡上，深水区的水深为0.531 m，复合斜坡平均坡度为1∶10.2。经过斜坡后波浪在等水深的浅水段传播，浅水区的水深为0.031 m。模拟波浪为不规则波，有效波高HS=0.075 m，谱峰周期TP=1.5 s。

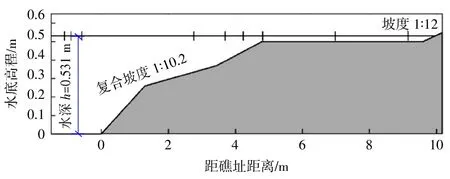
图2 Demirbilek 和Nwogu 的试验布置示意图Fig.2 Schematic diagram of Demirbilek and Nwogu experimental layout

数值模型参数：空间步长Δx=0.05 m，时间步长Δt=0.002 s，底摩擦系数fw=0.011，换算成谢才系数（Chezy Number）为55。在出口处布置1~2倍波长的海绵层。模型模拟时长为900 s，模拟100 s后波浪特征趋于稳定，稳定后的波浪用作统计分析。

沿程波高的数模值和物模值对比见图3，试验结果表明波高的数模试验值与物模试验值比较一致，说明模型可用于不规则波在复杂地形上的传播模拟。

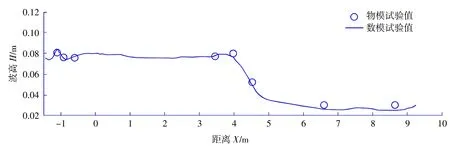
图3 Demirbilek 和Nwogu 物模试验值与MIKE21 BW 模型有效波高试验值对比Fig.3 Comparison of the experimental values of the Demirbilek and Nwogu physical model with the experimental values of the effective wave height of the MIKE21 BW model

3 计算结果分析

3.1 离岸方向HS 空间分布

3.1.1 正向入射波况

在不规则波入射直墙后反射的情况中，也将最大波高Hmax值处视为腹点，最小波高Hmin值处视为节点。本文采用两种波浪周期求得波长值进行分析，分别为谱峰周期TP对应波长LP和平均周期对应波长L。

图4 为对3 种主波向为0°的工况结果进行统计得到的各测点的HS。图中x 轴为距直墙相对距离s/LP或s/L，s 为距直墙实际距离，m；LP为入射波当前水深谱峰周期TP对应的波长值，m；L为入射波当前水深平均周期对应的波长值；y 轴为该点有效波高HS与入射波有效波高HS0的比波高HS/HS0。

图4 主波向为0°时直墙前的波高空间分布曲线Fig.4 Spatial distribution curve of wave height in front of a straight wall when the main wave direction is 0°

相对距离分别为s/L、s/LP时，不同工况下的波高空间分布曲线一致，其中相对距离为s/LP时，其曲线的腹点和节点的分布位置与规则波入射直墙反射后形成的驻波相同。在远离直墙的方向上，腹、节点处的波高值变化很大，振幅随着离堤距离的增加变小，2 个平均波长距离后腹、节点处的波高值变化与平均波高之比小于5%。根据波高与波浪能量存在H2-E 的关系，波浪入射直墙一定时间后，直墙前波能为2E，HS为入射波的倍，即HS/HS0≈1.4，而试验工况离堤距离达到一定值，波高分布曲线稳定后腹点处的比波高值在1.4 左右，这也说明了试验的合理性。这表明不同工况的直墙前波高空间分布取决于入射波当前水深下的波长，其中谱峰周期TP对应波长LP与之关联性最强。

3.1.2 斜向入射波况

限于篇幅，在此给出平均周期为12 s 时的不同主波向工况条件下的有效波高分布图及其腹点包络线，各入射波向波况下波高空间分布曲线如图5 如示。

图5 各入射波向波况下波高空间分布曲线Fig.5 Wave height spatial distribution curve under various incident wave directions and wave conditions

在靠近直墙的部分，主波向为0°的工况波高整体高于斜向入射的工况，且入射角度越大，比波高整体越低。当将波浪分解成横向、纵向传递，入射角度越小，正向传递的波浪能量越大，直墙前波浪的反射、叠加作用越大。但在远离直墙一定距离之后，由于斜向入射条件下的波高空间分布曲线整体相位被拉长，腹、节点的分布并不均匀，这是因为在远离直墙的位置，由于海浪的多向性，叠加作用强于主波向正向的工况，主波向角度大的曲线不一定低于主波向角度小的曲线，靠近直墙的腹点不一定比远离直墙的腹点高。直墙上的比波高值普遍小于2。由图5 可知，不论何种波况下，直墙前平面波高最低点为离墙最近的节点处，且该点波高比之后的节点处波高值小很多。

3.2 反射后腹点、节点间距Lf 与波长L 的关系

分别对腹点和节点的间距统计分析，Lf与L的关系尚不明确，下面通过弥散方程以及试验数据探讨两者之间的联系。首先确定Lf如何统计分析，Lf的测量方式有两种，一种是腹点的间距Lf1，第二种是节点的间距Lf2。将各种工况的波高空间分布曲线中，根据上述对不规则波入射直墙后的腹点、节点的判断方式对腹点、节点的位置和波高值进行统计，相邻的腹点、节点的间距即为Lf的计算方法。将各工况的Lf1和Lf2统计，并引入公式计算其离散度σ。其表达式如下：

由表2、表3 可知，腹点和节点在主波向为0°时分布均匀，它们的间距可以整体被考虑，在主波向角度变大时，分布不再均匀且整体并无明显规律。

表2 HS 统计中各波况Lf1 的离散度Table 2 The dispersion degree of each wave condition Lf1 in HS statistics

表3 HS 统计中各波况Lf2 的离散度Table 3 The dispersion degree of each wave condition Lf2 in HS statistics

根据3.1 节中对主波向正向入射的波况，波高空间分布曲线与当前水深、谱峰周期对应波长LP，再加上入射角度、叠加作用等因素影响，直墙前Lf、T 和L 的关系有待进一步确定。受限于篇幅，下面只列出了与Lf值对应关系最强的LP的计算结果和结果分析。

3.2.1 正向入射波况

表4 直墙前第1 个节点和其相邻腹点中点比值Table 4 The ratio of the midpoint between the first node in front of the straight wall and its adjacent antinode

表5 正向入射时各波况下的Lf /（1 2Lp）Table 5 LLp）under each wave condition at normal incidence f /（1 2主波向θmain/（°）平均周期/s 8 1.02 1.01 1.01 0 10 12

3.2.2 斜向入射波况

随着主波向角度的变大，Lf值的离散度增大，波高分布曲线变得越来越不规则，很难得到准确的与L 的关系式，难以计算出腹点或节点的准确位置。

由表4 可知，对于不同入射方向，第1 个节点与相邻腹点的中点吻合。为了讨论方便，将直墙前第1 段腹点间距定义为L1f。即在L1f中，腹点和节点的对应关系不变。因此可以通过入射波况确定L1f对应腹点、节点的位置，可见对直墙前第1 段腹点间距和波长的讨论是有意义的。下面列出L1f与Lp以及不同入射角θmain的对应关系。

在其他入射波要素相同的情况下，随着主波向角度θmain的变大，L1f变大。

表6 各波况下的L1f/（1 2cos θmain Lp）Table 6 L1f/（1 2cos θmain Lp）under various wave conditions主波向θmain/（°）平均周期/s 8 10 12 1.02 1.01 1.01 11.25 0.97 1.01 1.00 22.5 0.98 1.00 1.03 33.75 0.99 0.98 1.00 45 0.98 1.00 1.02 0

3.3 直墙前HS 横向切面的空间分布情况

在波浪正向入射的试验中，直墙前横切面上的等波高线大多与直墙平行，由于入射波是多向不规则波，等波高线不严格平行十分正常；在波浪斜向入射的试验中，直墙前的等波高线与横切面并不平行，波高分布呈现相位差。

4 结语

1）多向不规则波入射后，离岸方向有效波高空间分布情况如下：主波向正向时，不同周期的条件下，堤前相同相对距离s/LP内有效波高空间分布曲线一致，腹、节点分布规律与规则波入射直墙的波况一致，在远离直墙方向腹点对应的比波高值逐渐变小，节点对应比波高值逐渐变大；斜向入射波况中，随着主波向偏离法向入射的角度变大，波高分布曲线不规则程度变大，腹、节点间距变大且不均匀；各工况在距离直墙一定距离后波高值趋于稳定，比波高值在1.4 左右；整体波高分布最小值处为堤前第1 个节点，且该点波高远小于其他节点处波高。

2）多向不规则波入射直墙后，腹、节点间距与谱峰周期计算得到波长LP有关。正向入射时，腹点间距Lf1相较与节点间距Lf2离散度较小，腹点间距Lf1与LP关系式为斜向入射时，堤前第1 段L1f与 LP以及主波向角度θmain对应，关系式为以上关系式可以依据入射波确定直墙前两个腹点的位置和间距以及第1 个节点的位置，在工程实践中可以考虑将泊位或浮码头的位置设置在第1 个节点位置及其位置附近。

3）波浪正向入射的试验中，直墙前横切面的波高分布基本为等波高线；波浪斜向入射的试验中，直墙前的等波高线基本不平行于横切面，波高分布出现相位差。