CPM 和PERT 技术在综合交叉工程的应用
王晓东
(中交四航局第二工程有限公司,广东 广州 510300)
0 引言
综合交叉工程是指作业空间小但项目投资大,且涉及学科、专业和施工队伍多的工程。建设空间小决定了工程无法在有限的空间内投入足够的资源,无法通过“以资源换时间”的方法来满足施工进度的要求;同时因为涉及学科及专业较多,不同工序需不同工种来完成,且交界面众多。如何在工程交界面众多、工序繁杂、工期要求严格的限制下,合理制定项目进度计划,合理安排工序,做到项目进度可控,避免出现超期现象,是综合交叉工程项目计划管理的一大难题。需应用到项目计划管理的手段,目前应用比较广泛的方法是关键路径法(CPM)和计划评审技术(PERT),两者有机结合,可以获得更显著的效果[1]。但是实际工程建设中,现场工程师应用较多的是关键路径法,很少使用计划评审技术。
关于CPM 和PERT 技术的应用,国内已有不少专家学者进行了相关研究工作。赵葆等[2]结合CPM 和PERT 对某石化项目的施工进度计划进行了优化;金勇[3]利用贝叶斯网络提出了改进的PERT技术;陈芳等[4]提出了基于PERT 的不确定因素影响下的生产进度评估方法;王赛等[5]将关键路径法(CPM)运用到国防阵地重型防护设备的制造安装项目进度控制中,提出了项目工期优化算法;金丰[6]和尹好[7]采用PERT 技术分别对某公司轻卡汽车开发项目和某有线电视工程的工期进行了估计。虽然已有相关学者针对PERT 技术进行应用及改进模型的探索,有部分学者开展了CPM 与PERT的结合应用,但并未对网络计划技术的真实应用情况进行对比研究,并没有充分验证技术及模型的可信度。本文以港珠澳大桥沉管隧道最终接头为背景,该工程在实际建设过程中只形成了甘特图为项目计划管理成果,并未采用CPM 和PERT相关技术,但实施过程中相关理念和数据与前述技术是相契合的;因此,本文对最终接头整个推进过程中的实际工作进行复盘,尝试将CPM 与PERT 技术应用于综合交叉工程的流程优化,以此验证实际工期与模型推演优化的差距,为类似工程在网络计划技术应用提供参考。
1 依托工程概况及网络计划技术简介
1.1 港珠澳大桥沉管隧道最终接头简介
港珠澳大桥岛隧工程包含1 条长6.7 km 的沉管隧道,其中沉管段长5 664 m,由33 个管节和1 个最终接头组成,最终接头位于E29 与E30 之间[8]。最终接头块采用钢壳混凝土组合结构,由2个对称的倒直角梯形单元组成,两个单元间设置永久管节接头设施。在组装、运输和安装阶段,通过临时预应力将2 个对称单元连接成整体,安装后予以解除。最终接头的钢壳结构制造和混凝土浇筑分别在钢结构加工厂和沉管预制工厂两地进行,采用驳船进行运输并做为混凝土浇筑的场地,最后采用浮吊进行水下快速安装[9-12]。
1.2 网络计划技术概述
网络计划技术采用有向网络图来表达计划中各项活动的进度和它们之间的相互关系,主要分为计划编辑阶段与实施跟踪阶段。在计划编制阶段,主要进行WBS 分解、确定各项工作的逻辑关系和持续时间以及资源配置、网络图绘制并计算各类参数,在考虑一定约束条件的情况下拟定总体计划。在实施跟踪阶段,则主要根据实施情况,按期执行计划并根据反馈情况进行计划调整及优化。整个过程为动态过程。
CPM 技术,即关键路径法,是用寻找关键路径及其时间长度来确定项目的完成日期与总工期的方法。对各关键活动,优先安排资源,挖掘潜力,采取相应措施,尽量压缩需要的时间;对非关键路径活动,在不影响工程完工时间的条件下,抽出适当资源,用在关键路径上,以缩短工程工期,合理利用资源。
PERT 技术,即计划评审技术,发端于美国海军北极星导弹核潜艇研制的计划和控制[13]。其应用可以理解为工程工期的概率分析,与CPM 技术不同的是,CPM 中工序时间是确定的,而PERT中单个工序时间是随机变量,进而完工工期也是随机的;其应用的基本原理是完工工期从概率统计角度来看服从正态分布,并以此得出实现具体某一个时间节点工期的完成概率。具体的操作方法是:由最熟悉有关作业的人员利用三点估计法估算出关键线路上每项作业所需要的最乐观时间A、最可能时间M 和最悲观时间B,进而求出每项作业的平均持续时间 Ti=(A+4×M+B)/6 和标准差 σi=(B-A)/6(i 为对应各项工序),完工工期 T作为随机变量则服从一个数学期望TE、标准差σ的正态分布(TE=∑Ti,σ2=∑σi2),以此可求出完成要求工期的概率,同时也可求出某个完工概率条件下的完工工期。
2 工期要求下的完工概率分析
最终接头施工的整体工期要求:隧道贯通时间为2017 年6 月15 日,钢壳制造开始日期为2016 年10 月10 日,因此最终接头整体施工工期(不考虑节假日、周末)为249 d。
2.1 对各分部分项工程任务分解
最终接头相较沉管隧道管节,虽然体积小,但是涉及范围广,同时须在不同的地点完成相应的作业。在不同的地点有一定的逻辑衔接关系。因此,按照地点划分的原则,将最终接头整体施工分为六大部分并在此基础上,针对其中几个施工地点工序较多、涉及施工队伍较多的分部工程进行再细分。
根据以上的原则和分析,按照一定的逻辑关系和顺序,得到该项目的工程任务分解图,如图1 所示。
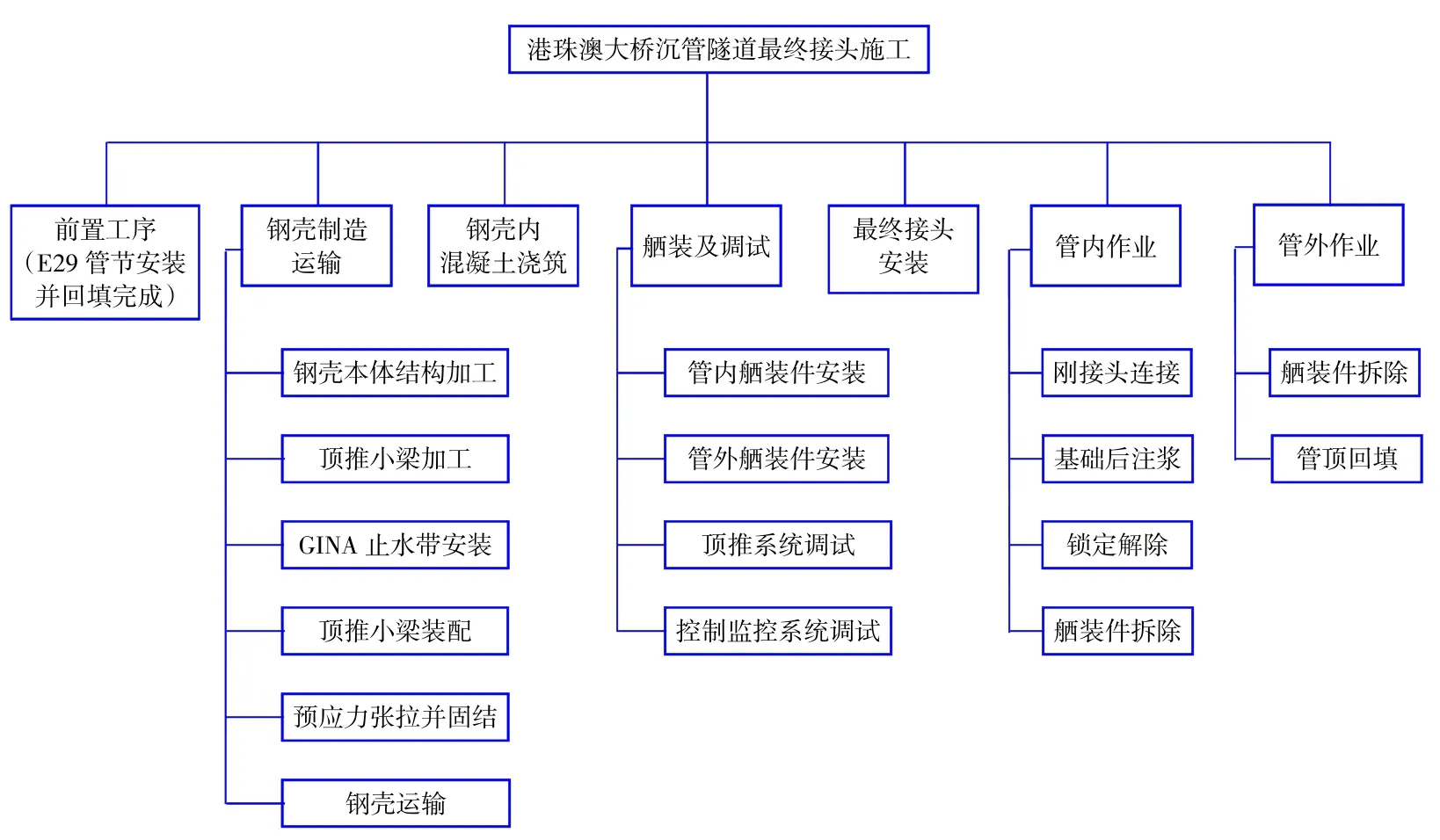
图1 最终接头工作任务结构分解图Fig.1 Work breakdown structure of closure joint project
2.2 项目任务分解清单
对分部工程进行进一步分解和定义,为分部、分项工程定义名称并设立工作代码、估算每个分项工程的工期天数。各工序三点估计法工期参数的选取原则分为以下3 类:
1)成熟或已应用工艺,调取该分部分项在本项目不同管节的完成工期进行数据分析,时间最长为B、时间最短为A、所有数据的平均值为M;例如舾装件安装、舾装件拆除,则参考了已完成33 个管节相关作业的数据。
2) 新工艺但是有类似工法,则参考类似工法,同样采取数据分析,并考虑与本项目相应参数相结合,最长、平均、最短分别对应B、M、A;例如钢壳本体结构加工则参考了造船的工期,按照同等钢结构的重量及难易程度相当的要求,选取了多艘船舶的造船时间进行了数据分析。
3)新工艺但是无类似工法参考,则将该工艺流程细化并对可能的困难进行分析,然后分别对劳务分包单位、施工单位、总承包单位进行交底,3 个单位在背靠背的前提下分别对该分项工程的所需工期进行制定,3 个工期数据最短、中等、最长分别对应A、M、B;例如刚接头连接。
工期确定后,根据施工工艺和各分项工程间的关系将工作中的具体内容拆分,并依据逻辑关系制表(见表1)。
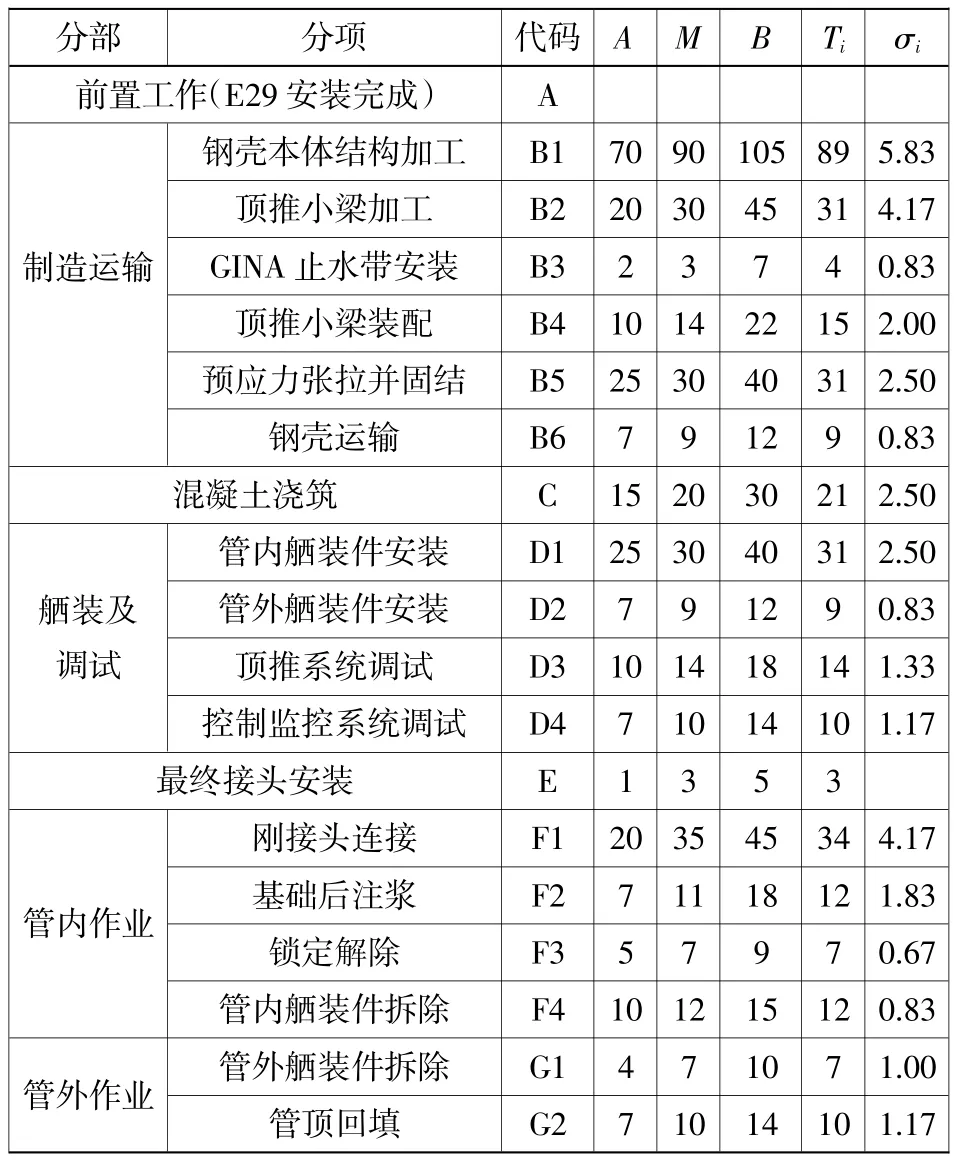
表1 分部分项工程项目活动分解表Table 1 Activity breakdown table of divisional and items works d
2.3 绘制进度网络图
根据前述的项目活动分解清单,以及最初的最终接头总体施工流程图,进一步理清各活动间的关系,以此为基础绘制双代号网络图(图2),因A 工作的前置时间充裕,不会影响最终接头安装,只绘制逻辑关系,工期影响不考虑。由图2可以得出,关键线路为1—2—3—4—5—6—7—8—12—13—14—15—16—19,时长为264 d,显然超过了要求工期的249 d,因此需完成249 d 工期的概率,以此确定是否可控。
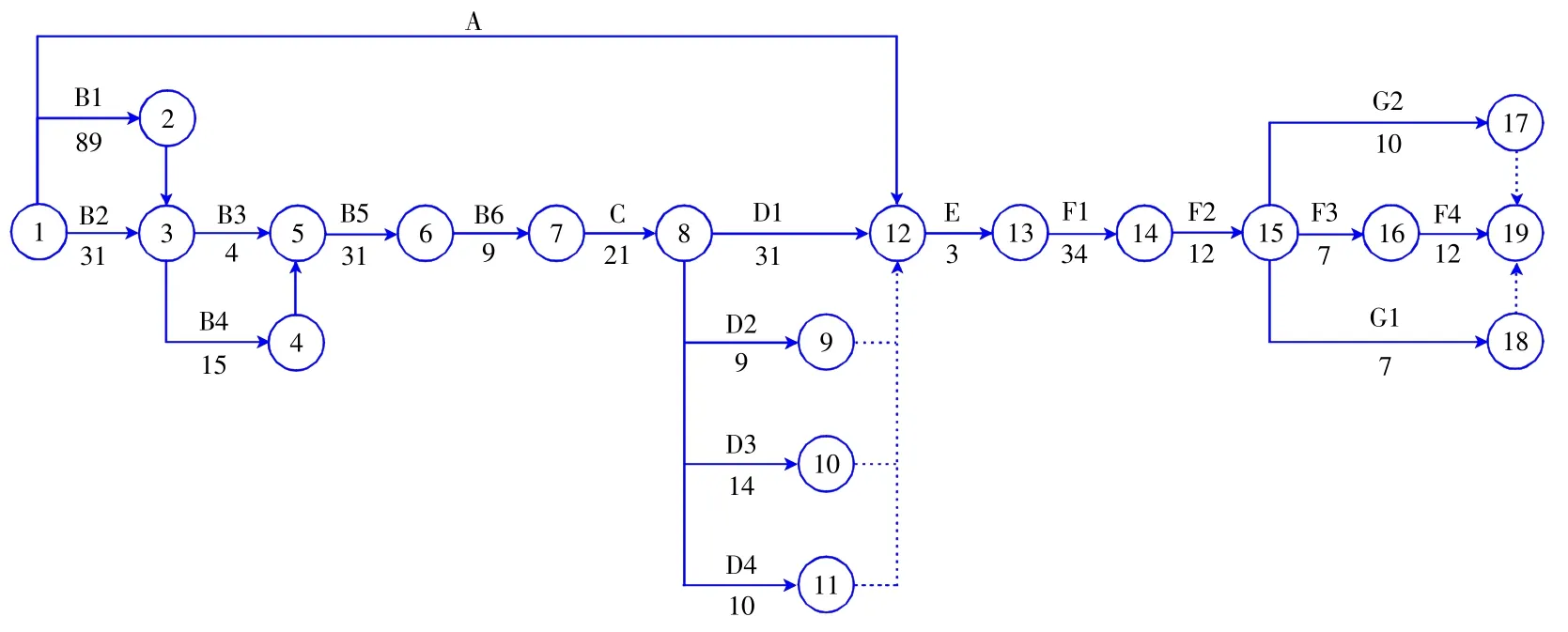
图2 最终接头工程进度计划网络图Fig.2 Network chart of closure joint project schedule
2.4 计算工期完成的概率
首先计算关键线路上各关键工序(B1、B4、B5、B6、C、D1、E、F1、F2、F3、F4)的平均持续时间Ti和标准差σi(表1),进而得出TE=263.34 d 和σ=8.932 d,因此最终接头完工工期T 服从一个数学期望为263.34 d、标准差为8.932 d 的正态分布。前述要求工期T=249 d,由概率论相关计算方法可得出249 d 内完成最终接头工程建设的概率P(T≤249)=φ[(249-263.34)/8.932]=φ(-1.61),查标准正态分布表,得φ(-1.61)=0.053 7。则可知在249 d 内完成的概率为5.4%,显然极大概率是无法满足要求的,因此需要在此基础上进行工艺或工序的优化。
3 工序优化及完工概率计算
3.1 各分部分项工程任务再分解
本工程关键工序工期制定时就没有考虑节假日、假期等影响,同时在许多关键工序还需要考虑24 h 作业,因此压缩关键工序时间实施困难;另外,非关键工序项目较少,几乎所有工序均为关键工序,且非关键工序耗费时间相对较短,因此在非关键工序上挖掘潜力的可能意义不大。因此网络图的优化,从“尽量采用平行工序和交叉工序”中着手,经过多次的工艺推演,目前的关键工序均有严格的逻辑关系,无法提前或滞后;然而,部分关键工序涉及施工内容较多,可在原有基础上继续分解,并重新安排工序,形成工作任务细化分解表和子分项工程的工作分解表(如表2 所示),使得部分占用关键线路的工序不占用关键线路。

表2 舾装及调试子分项工程工作分解表Table 2 Activity breakdown table of outfitting and commissioning items and subitems works d
细化后,管内舾装件安装工序中的D11、D12、D13 工序,管外舾装件安装工序中的D21、D22、D23、D24 工序,以及 D31、D32 和 D41 工序均可在钢壳制造完成后,两个1/2 结构组拼过程中采用平行或者交叉的作业完成,造成高流动性混凝土浇筑时间会比原定计划多4 d,即C 工作由最初估算的20 d 调整为24 d。
3.2 绘制任务再分解后的网络图
根据任务再分解后项目活动分解清单,绘制优化后的双代号网络图(图3),由图3 可以得出,关键线路为1—2—3—4—5—14—15—16—17—18—23—24—25—26—27—29,时长为 247 d,比要求工期249 d 要短,初步计算可以满足工期,为充分论证工序安排的合理性以及应对风险的能力,还需对完工概率进行计算。
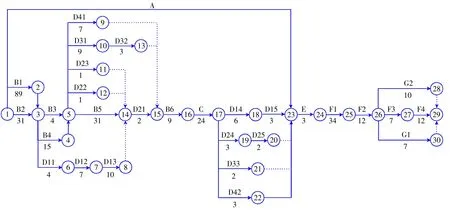
图3 优化后最终接头工程网络示意图Fig.3 Optimized network chart of closure joint project
3.3 计算工期完成的概率
首先计算关键线路上各关键工序(B1、B4、B5、D21、B6、C、D14、D15、E、F1、F2、F3、F4)的平均持续时间Ti和标准差σ(i表1、表2),进而得出TE=247.85 d 和σ=8.61 d,因此最终接头完工工期T 服从一个数学期望为247.85 d、标准差为8.61 d 的正态分布。前述要求工期T=249 d,由概率论相关计算方法可得出249 d 内完成最终接头建设的概率P(T≤249)= φ([249-247.85)/8.61]=φ(0.13)=0.551 7,则可知在 249 d 内完成的概率为55.17%。
4 工序优化措施及实际完成情况对比
4.1 网络图优化后采取的措施
根据计算情况,预计工期小于要求工期的概率为55%,从概率上讲,完成要求工期的可能性是比较大的。影响整体完工工期的主要是标准差(或方差)比较大的关键工序,即B1 钢壳制造;F1 刚接头连接。针对这两个关键工序,采取一系列的措施。
B1 工序工期保障措施:钢壳制造整体工序安排上,减少室外作业,从板单元到整体拼装均在场内进行,不会受风雨天气影响,采用流水线生产作业[11]。
F1 工序工期保障措施:影响刚接头连接的主要原因为狭窄空间焊接,起重能力有限,装配难度大,不确定性大,通风环境差,这些都将导致工期延误;在此基础上,进行陆上等比例工况演练,定人定岗定位置,在最终接头安装完成后,所有人员有序进行;优化施工工艺,简化装配流程,可以在陆上完成的尽量不在水下完成[14]。
4.2 实际完成情况对比分析
正式施工过程中,最终接头实际最终完成的贯通时间为2017 年6 月30 日,总时长为264 d,影响工期整体进度的为钢壳结构制造[12]。可见方差较大的分项工程应作为项目实施过程中重点关注对象,同时也说明F1 工序采取了较为有利的措施,最终在实际实施中并未对总工期有较大影响。以264 d 为实际完工工期,利用前述完工工期所服从的正态分布,反推264 d 工期所对应的完工概率,可知P(T≤264)=φ[(264-247.85)/8.61]=φ(1.876)=0.969 7。
可见,实际完工工期在前述的正态分布中,对应的完工概率为96.9%,因此对应于该类综合交叉工程,在对工期进行精确的估计时,应选取96%左右的概率下求得实际的工期天数与实际情况更为契合。
5 结语
1)利用CPM 技术绘制网络图能够清晰地反映出工程多个关键工序任务之间的逻辑关系,明确关键路径和工作;并结合PERT 技术可以对工期进行估计,计算实现完工工期的概率,以判断工期布置是否合理;并可利用WBS 分解原理对工作任务进行再分解,通过“尽量采用平行工序和交叉工序”实现工期的优化,并制定合理可行的进度计划。
2)通过三点估算法,既可为完工工期的概率做基础,也可找出通过对各工序中标准差大小进行排序以此作为重点关注的工序;本文选取的工程背景,在正式工程建设中,对工期进度造成较大影响的恰恰是标准差最大的一项工序。
3)通过对比实际工期反推工期完工概率,得出实际工期在原模型推演的正态分布中完工概率约为96%;因此,在后续类似综合交叉工程中,选取96%左右的概率下求得实际的工期天数,可作为项目部外控指标,减少总承包单位的工期风险;同时也可以选取60%~80%的完工概率下求得实际工期天数,作为内控指标,可根据内控指标及时调整资源的配置。

