基于对勾函数的新型天然气压缩因子计算关联式
王艺晨 叶继根 吴淑红
中国石油勘探开发研究院
天然气压缩因子(Z因子)是石油天然气工业中最重要的流体物性参数之一。在油气藏工程领域,准确计算出天然气的压缩因子,对于天然气储量计算、开发方案编制和开发指标预测至关重要。一旦天然气压缩因子计算结果不够准确,就会使储量计算结果存在较大误差,油气开采也会遭受一定的经济损失[1]。因此,在矿场实践中快速而又准确地确定天然气压缩因子尤为关键。
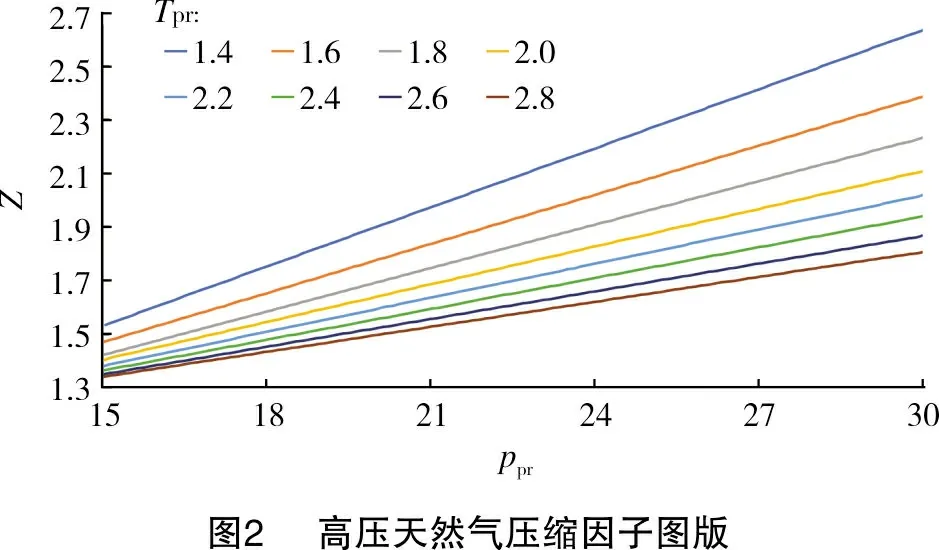
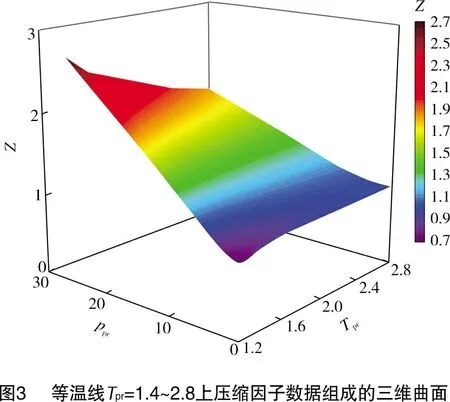
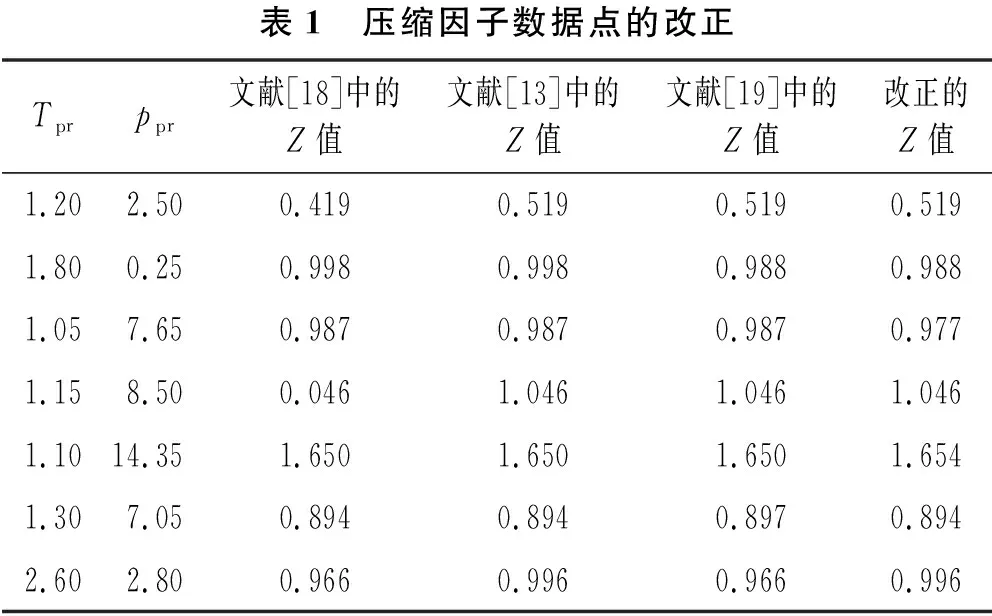
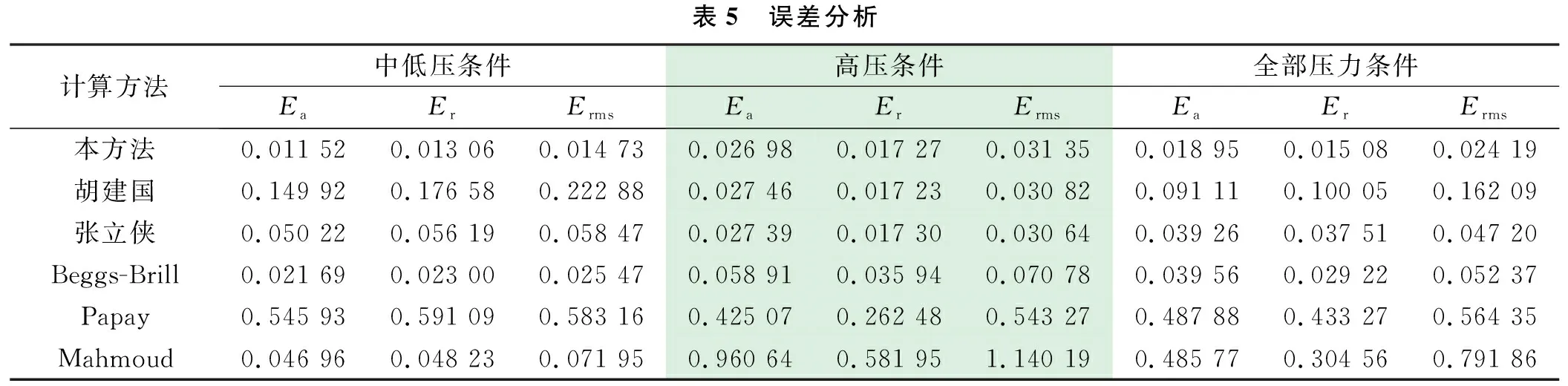
确定天然气压缩因子的方法分为实验测定法、图版法和计算法。实验测定法虽然直接可靠,但是具有周期长、成本高和费时费力的缺点;图版法则存在人工读值误差,难以保证精度;而计算法简单实用,得到了广泛运用。计算法又可分为隐式计算法和显式计算法。隐式计算法是指利用状态方程拟合天然气压缩因子数据、进而得到隐式计算公式的方法,例如Hall和Yarborough[2]利用Starling-Carbahan状态方程拟合压缩因子数据得出的HY方法、Dranchuk等[3]利用BWR状态方程得出的DPR方法、Dranchuk和Abou-Kassem[4]利用BWRS状态方程得出的DAK方法。这3种经典方法虽然在0.2≤ppr≤15范围内具有较高的计算精度,但是在15 为了提高0.2≤ppr≤30压力范围内天然气压缩因子的计算精度与计算效率,本研究基于天然气压缩因子图版的曲线形态,利用非线性曲面拟合的方法,选择对勾函数对压缩因子图版进行整体拟合,提出了一种新型天然气压缩因子显式计算公式,以期为矿场实践提供一种快速准确的天然气压缩因子预测方法。 1942年,Standing和Katz[12-13]基于对应状态原理,根据实验数据绘制了天然气压缩因子图版(见图1、图2)。此后,该图版成为石油行业中天然气压缩因子的标准图版。大多数天然气压缩因子计算模型都是根据Standing-Katz图版回归拟合而成[9],但是复杂的曲线形态给天然气压缩因子计算公式的拟合造成了极大的困难。 由于未能找到恰当的函数来拟合整个Standing-Katz图版(见图1和图2),学者们通常只选取图版中某一规律性较强的区域中的压缩因子数据进行拟合。由于选取的数据点不同,采用的拟合方法也不同,导致各种计算模型的计算精度及适用条件也不尽相同。例如Heidaryan等[10]仅使用0.2≤ppr≤15、1.2≤Tpr≤3.0范围内的1 220组数据进行拟合,因此提出的经验公式在15 由图1可以看出,天然气压缩因子在0.2≤ppr≤15.0、1.05≤Tpr≤3.00条件下与拟对比压力、拟对比温度之间呈现出复杂的非线性函数关系。在各条等温线上,压缩因子随着拟对比压力的增大均呈现先减小后增大的趋势;在曲线上升段,拟对比压力越大,压缩因子与拟对比压力的关系越趋近于线性关系。由图2可知,当15 选取中低压图版和高压图版上Tpr=1.4、1.6、1.8、2.0、2.2、2.4、2.6、2.8八条等温线的数据合为一个整体,绘制出三维曲面图(见图3)。由图3可以看出,曲面形态十分光滑,无明显间断和突变。因此,天然气压缩因子的中低压图版和高压图版有着较好的连续性,无需分区进行研究,可利用三维对勾曲面函数对图版曲面进行整体拟合,尝试解决压缩因子图版拟合困难的问题。 Poettman 和Carpenter[18]、Katz等[13]和Smith[19]分别给出了中低压图版(见图1)的数值化结果,共计5 940个数据点。经过研究比对,上述学者给出的数值化结果中有7个数据点疑似有误,因为在这些点处压缩因子数值存在突变的情况。文献[6]和文献[17]仅对其中5个有误的数据点进行了更正,需要补充完善。根据附近数据点的取值和压缩因子图版的曲线延伸趋势,对这7个有误的压缩因子数据做出改正,如表1所列。 表1 压缩因子数据点的改正Tprppr文献[18]中的Z值文献[13]中的Z值文献[19]中的Z值改正的Z值1.202.500.4190.5190.5190.5191.800.250.9980.9980.9880.9881.057.650.9870.9870.9870.9771.158.500.0461.0461.0461.0461.1014.351.6501.6501.6501.6541.307.050.8940.8940.8970.8942.602.800.9660.9960.9660.996 将高压图版(见图2)进行数值化处理,得到1 048组数据。基于改正后的中低压天然气压缩因子图版数值化结果和高压天然气压缩因子图版数值化结果(总计6 988组数据),以ppr和Tpr为自变量,以Z为因变量,以对勾曲面函数为目标函数,利用Matlab编写相关程序,进行大量的非线性曲面拟合,最终得到0.2≤ppr≤30.0、1.05≤Tpr≤3.00范围内天然气压缩因子计算模型,见式(1)~式(4): (1) (2) (3) (4) 式中:Z为天然气压缩因子,无量纲;ppr为天然气拟对比压力,无量纲;Tpr为天然气拟对比温度,无量纲;a1~a18为拟合系数,无量纲。 根据非线性最小二乘拟合的结果,式(2)~式(4)中系数a1~a18的值如表2所列。 表2 计算模型中的系数值系数拟合值系数拟合值a10.060 53a103.941 32a20.250 11a11-15.453 89a3-0.006 50a121.794 60a43.763 35a13-0.006 77a56.919 30a14-0.001 16a6-39.801 13a155.897 69a738.344 47a166.111 33a8-8.810 56a170.391 16a90.554 71a18-0.404 03 利用数理统计学中的平均绝对误差Ea、平均相对误差Er和均方根误差Erms来评价拟合效果,其计算公式见式(5)~式(7)。天然气压缩因子图版20条等温线拟合效果如表3所列。 (5) (6) (7) 表3 各条等温线的拟合效果TprEaErErms1.050.022 570.045 750.032 761.100.011 420.017 830.015 841.150.008 070.010 850.012 291.200.009 890.013 020.015 131.250.012 550.015 590.017 181.300.015 060.018 580.019 621.350.013 670.016 630.018 261.400.012 340.012 130.019 531.450.011 640.013 220.014 881.500.009 420.010 440.012 141.600.007 250.006 210.010 211.700.003 310.003 570.004 631.800.005 640.004 160.009 021.900.005 760.005 550.007 952.000.009 130.007 610.013 972.200.013 480.011 570.020 332.400.016 410.014 240.024 432.600.018 640.016 070.026 742.800.021 070.017 790.029 683.000.021 690.019 890.026 85所有等温线0.012 510.013 590.017 57 式中:ZCal为天然气压缩因子计算值,无量纲;ZMea为天然气压缩因子实测值,无量纲。 根据表3中的统计学指标,从Ea上来看,20条等温线的Ea均较小,均在0.003 3~0.022 6之间;从Er上来看,1.10≤Tpr≤3.00,19条等温线的Er值较小,均在0.02以下,Tpr=1.05时,Er值稍大,但也在误差允许的范围内(0.05以下);从Erms上来看,20条等温线的Erms值均较小,均在0.004 6~0.032 8之间。因此,利用式(1)~式(4)对Standing-Katz图版数据进行拟合能够取得良好的效果。 为了检验本研究中提出的新型天然气压缩因子计算方法在实际应用中的准确程度,选用Satter和Campbell[20]、Buxton和Campbell[21]发表的237组中低压条件下压缩因子的实测数据以及郭绪强等[22-23]发表的219组高压条件下压缩因子的实测数据作为验证实例。表4给出了上述作为验证实例的天然气试样的组成数据。 由于上述天然气试样中含有非烃类组分,因此需要使用Wichert-Aziz校正方法对天然气的拟临界压力和拟临界温度予以校正[24],其计算公式如下: 表4 天然气样品的组成数据组分摩尔分数最大值最小值平均值CO20.201 600.002 380.061 19N20.032 280.003 390.012 60H2S0.197 000.047 000.100 00CH40.929 950.584 100.824 34C2H60.286 700.033 230.080 39C3H80.028 680.011 500.021 22i-C4H100.010 770.002 570.005 99n-C4H100.007 780.002 600.005 02i-C5H120.002 810.000 890.001 71n-C5H120.001 630.000 570.001 02n-C6H140.001 450.000 320.000 74n-C7H160.001 330.000 000.000 51n-C8H180.000 690.000 000.000 22 (8) (9) ε=[120(M0.9-M1.6)+15(N0.5-N4)]/1.8 (10) 将本研究提出的新型天然气压缩因子计算方法以及胡建国、张立侠、Beggs-Brill、Papay、Mahmoud方法的计算结果进行比较,如图4所示。利用平均绝对误差Ea、平均相对误差Er和均方根误差Erms来分别评价中低压条件和高压条件下各方法计算结果与实测值之间的误差,结果如表5所列。 由图4可以直观地看出,本研究提出的新型天然气压缩因子计算方法的计算结果数据点均匀而又紧密地分布在零误差线周围,说明计算结果与实测值接近,计算结果准确程度较高,而其他方法的计算结果数据点分布散乱且距离零误差线较远,计算精度和计算稳定性较差。 由表5中的统计学指标可知,在中低压条件下,本研究提出的新型天然气压缩因子计算方法的Ea值、Er值和Erms值均小于胡建国、张立侠、Beggs-Brill、Papay和Mahmoud方法;在高压条件下,本研究提出的新型天然气压缩因子计算方法的Ea值、Er值和Erms值与胡建国方法、张立侠方法相近,小于Beggs-Brill、Papay和Mahmoud方法;总的来看,本方法的Ea值仅为0.018 95,Er值仅为0.015 08,Erms值仅为0.024 19,小于其他5种显式或隐式的天然气压缩因子计算方法。因此,本研究提出的显式计算公式更为准确,计算稳定性更高,在0.2≤ppr≤30.0压力范围内均具有较高的计算精度。 表5 误差分析计算方法中低压条件高压条件全部压力条件EaErErmsEaErErmsEaErErms本方法0.011 520.013 060.014 730.026 980.017 270.031 350.018 950.015 080.024 19胡建国0.149 920.176 580.222 880.027 460.017 230.030 820.091 110.100 050.162 09张立侠0.050 220.056 190.058 470.027 390.017 300.030 640.039 260.037 510.047 20Beggs-Brill0.021 690.023 000.025 470.058 910.035 940.070 780.039 560.029 220.052 37Papay0.545 930.591 090.583 160.425 070.262 480.543 270.487 880.433 270.564 35Mahmoud0.046 960.048 230.071 950.960 640.581 951.140 190.485 770.304 560.791 86 (1) 基于Standing-Katz天然气压缩因子图版的曲线形态,将中低压图版和高压图版视为一个整体,采用非线性曲面拟合的方法,得到了一种对勾函数形式的新型天然气压缩因子显式计算公式。拟合值与图版值的平均绝对误差仅为0.012 51,平均相对误差仅为0.013 59,均方根误差仅为0.017 57。本研究提出的方法拟合Standing-Katz图版数据效果良好,能够较为准确地表征图版数据。 (2) 实例验证结果表明,本方法的计算结果值与456组中低压或高压条件下的实测天然气压缩因子数据最为接近,平均绝对误差仅为0.018 95,平均相对误差仅为0.015 08,均方根误差仅为0.024 19,优于其余5种常用的显式或隐式计算方法。本方法在实际应用中的准确程度较高,适用范围更广。本方法推荐使用的压力温度条件为:0.2≤ppr≤30.0、1.05≤Tpr≤3.00。 (3) 本研究提出的新型天然气压缩因子计算方法形式简单,在计算时无需分区,也无需编程迭代,计算精度和计算效率较高。利用该方法能够在矿场实践中快速且准确地对天然气压缩因子进行预测。1 天然气压缩因子图版特征
2 公式拟合
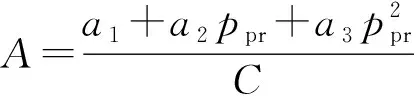


3 实例验证



4 结论

